01背包

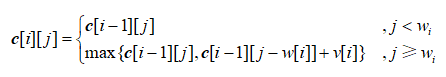
#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

const int N = 1010;

int m, n;
int f[N];

int main()
{
    cin >> m >> n;

    for (int i = 0; i < n; i ++ )
    {
        int v, w;
        cin >> v >> w;
        for (int j = m; j >= v; j -- )
            f[j] = max(f[j], f[j - v] + w);
    }

    cout << f[m] << endl;

    return 0;
}

完全背包

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 1010;

int n, m;
int v[N], w[N];
int f[N];

int main()
{
    cin >> n >> m;
    for (int i = 1; i <= n; i ++ ) cin >> v[i] >> w[i];

    for (int i = 1; i <= n; i ++ )
        for (int j = v[i]; j <= m; j ++ )
            f[j] = max(f[j], f[j - v[i]] + w[i]);

    cout << f[m] << endl;

    return 0;
}

多重背包

#include<iostream>
using namespace std;
const int N=110;
int v[N],w[N],s[N];
int f[N];
int n,m;

int main()
{
    cin>>n>>m;

    for(int i=1;i<=n;i++)
        cin>>v[i]>>w[i]>>s[i];

    for(int i=1;i<=n;i++)
        for(int k=1;k<=s[i];k++)
            for(int j=m;j>=v[i];j--)
                f[j]=max(f[j],f[j-v[i]]+w[i]);

    cout<<f[m]<<endl;
    return 0;
}

二进制拆分

#include<iostream>
using namespace std;
const int N=1010,M=2010;
int v[N],w[N],c[N];
int f[M];
int n,m;

int main()
{
    cin>>n>>m;
    for(int i=1;i<=n;i++)
        cin>>v[i]>>w[i]>>c[i];
    for(int i=1;i<=n;i++)
    {
        if(c[i]*v[i]>=m)//转化完全背包 
        {
            for(int j=v[i];j<=m;j++)
                f[j]=max(f[j],f[j-v[i]]+w[i]);
        }
        for(int k=1;c[i]>0;k<<=1)//二进制拆分（每个物品都拆成logci个）
        {
            int x=min(k,c[i]);
            for(int j=m;j>=v[i]*x;j--)//转化01背包 
                f[j]=max(f[j],f[j-v[i]*x]+x*w[i]);
            c[i]-=x;
        } 
    }

    cout<<f[m]<<endl;
    return 0;
}

单调队列优化

对于 f[i][j]，令 b[i] = min(a[i], j / c[i])
f[i][j] = max(f[i-1][j-k•c[i]]+k•w[i]) , 0≤k≤b[i]
观察 f[i][j] 会从哪些状态转移过来。
对于 {j-k•c[i] | 0≤k≤b[i]} 这些数，模 c[i] 都是同余的。
我们令 mod = j % c[i], div = j / c[i], 那么 j = div * c[i] + mod
得：j-k*c[i] = (div - k)c[i] +mod

则f[i][j] = max(f[i-1][mod + (div - k)c[i]]+k•w[i]) ,0≤k≤b[i]

用 k’ 替换掉 div-k
f[i][j] = max(f[i-1][mod + k’•c[i]]+(div-k’)w[i]) ,div-b[i]≤k’≤div
div和mod都是固定的，唯一要枚举的变量是k’,将常量div*w[i]提到外面
f[i][j] = max(f[i-1][mod + k’•c[i]]-k’•w[i]) + div•w[i], div-b[i]≤k’≤div

f[i][j] = max(f[i-1][mod + k’•c[i]]-k’•w[i]) + div•w[i] ，div-b[i]≤k’≤div
考虑范围：{mod, mod+c[i], mod+2c[i], mod+3c[i], …, j}
f[i][j] 就是求 j 前面的 (b[i]+1) 个数（div-b[i]≤k’≤div）对应的 f[i-1][mod+k*c[i]]-kw[i] 的最大值。
对于最外层 i 的枚举，b[i]+1 是固定的。
问题转化为求一个固定长度的滑窗内的最大值。

维护一个单调下降的队列。
每次加入的时候加入队尾，保证队头到队尾单调递减。
弹出队头，直到满足队头在滑窗内。
队头的值就是这个滑窗内的最大值。
这样这一步就是线性的。
我们枚举 mod，再枚举 div，求 f[i][j] 是用单调队列，总共是 O(V) 的。
总的时间复杂度仍然保持在了 O(NV)。
模板题

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
using namespace std;
const int N=1010,M=20010;
int f[2][M];
int q[M],num[M];//q存值，num存对应下标 
int n,m;

int main()
{
    cin>>n>>m;
    for(int i=1;i<=n;i++)//枚举物品种类 
    {
        int v,w,s;//分别对应体积,价值,个数 
        cin>>v>>w>>s;
        s=min(s,m/v);
        for(int mo=0;mo<v;mo++)//枚举余数 
        {
            int hh=0,tt=-1;
            for(int k=0;k<=(m-mo)/v;k++)
            {
                if(hh <= tt && k-s>num[hh]) hh++;//窗口内元素个数不超过s+1个 

                int t=f[i-1&1][k*v+mo]-k*w;
                while(hh <= tt && q[tt] <= t)
                    tt--;
                q[++tt]=t;
                num[tt]=k;
                f[i&1][k*v+mo]=q[hh]+k*w;
            }
        }
    }

    printf("%d\n",f[n&1][m]);
    return 0;
}

分组背包

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 110;

int n, m;
int v[N][N], w[N][N], s[N];
int f[N];

int main()
{
    cin >> n >> m;

    for (int i = 1; i <= n; i ++ )
    {
        cin >> s[i];
        for (int j = 0; j < s[i]; j ++ )
            cin >> v[i][j] >> w[i][j];
    }

    for (int i = 1; i <= n; i ++ )
        for (int j = m; j >= 0; j -- )
            for (int k = 0; k < s[i]; k ++ )
                if (j >= v[i][k])
                    f[j] = max(f[j], f[j - v[i][k]] + w[i][k]);

    cout << f[m] << endl;

    return 0;
}

例题

hdu1114

#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N=510,M=10010;
const int INF=0x3f3f3f;
int dp[M];//dp[j]表示放入重量为j的存钱罐面值之和最小值 
int val[N],w[N];//val[i]表示第i种硬币的面值，w[i]表示第i种硬币的重量 
int main()
{
    int t,E,F,W,n;//t个测试用例，E、F表示没装硬币和装了硬币之后的重量,W重量差值，硬币种类 
    cin>>t;
    while(t--)
    {
        cin>>E>>F;
        W=F-E;
        cin>>n;
        for(int i=0;i<n;i++)
            cin>>val[i]>>w[i];
        memset(dp,0x3f,sizeof(dp));
        dp[0]=0;
        for(int i=0;i<n;i++)//计算dp[j]
            for(int j=w[i];j<=W;j++)//比较此硬币放与不放是否能使得存钱罐内面值之和最小
                dp[j]=min(dp[j],dp[j-w[i]]+val[i]);
        if(dp[W]<INF)
            cout<<"The minimum amount of money in the piggy-bank is "<<dp[W]<<"."<<endl;
        else
            cout<<"This is impossible."<<endl;
    }
    return 0;
}

poj1276

#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int N=11,M=100010;
int n,m;
int c[N],w[N];
int f[M];

int main()
{
    while(~scanf("%d%d",&m,&n))
    {
        for(int i=1;i<=n;i++)
            scanf("%d%d",&c[i],&w[i]);
        memset(f,0,sizeof f);
        for(int i=1;i<=n;i++)
        {
            if(c[i]*w[i]>=m)//转化完全背包 
            {
                for(int j=w[i];j<=m;j++)
                    f[j]=max(f[j],f[j-w[i]]+w[i]);
            }
            else
            {
                for(int k=1;c[i]>0;k<<=1)//二进制拆分
                {
                    int x=min(k,c[i]);
                    for(int j=m;j>=w[i]*x;j--)//转化01背包 
                        f[j]=max(f[j],f[j-w[i]*x]+x*w[i]);
                    c[i]-=x;
                } 
            }
        }
        printf("%d\n",f[m]);
    }
    return 0;
}

hdu1712

#include<cstdio>
#include<cstring>
#include<algorithm>
#define maxn 105
using namespace std;
int a[maxn][maxn],dp[maxn];
int n,m;

int main()
{
    while(~scanf("%d%d",&n,&m))
    {
        if(n==0&&m==0) break;
        memset(dp,0,sizeof(dp));
        for(int i=1;i<=n;i++)
            for(int j=1;j<=m;j++)
                scanf("%d",&a[i][j]);
        for(int i=1;i<=n;i++)
            for(int j=m;j>=0;j--)
                for(int k=1;k<=j;k++)//用来枚举分组内的天数 
                    dp[j]=max(dp[j],dp[j-k]+a[i][k]);
        printf("%d\n",dp[m]);
    }
    return 0;
}

二维费用背包

二维费用01背包问题

* 花费1：精灵球数量

• 花费2：皮卡丘体力值

• 价值：小精灵的数量(每只精灵价值为1)

状态表示：f[i,j,k]表示所有只考虑前i个物品，且花费1不超过j，花费2不超过k的选法的最大值
注意：使得皮卡丘体力小于等于0的野生小精灵也不会被小智收服，因此皮卡丘的体力值需在V2 - 1时开始
在背包问题中，体积w与价值v是可以互逆的！
可以将f[i]表示为体积为i能装的最大价值，
也可以将f[i]表示为价值为i所需的最小体积。
两者等价，我们只需要选择范围较小的那维作为体积就可以了！
这直接影响到时空复杂度。（转自墨染空大佬）
1.(体力、精灵球数为费用、精灵数为价值) O(nmk)

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 1010, M = 510;

int n, V1, V2;
int f[N][M];

int main()
{
    cin >> V1 >> V2 >> n;
    for (int i = 0; i < n; i ++ )
    {
        int v1, v2;
        cin >> v1 >> v2;
        for (int j = V1; j >= v1; j -- )
            for (int k = V2 - 1; k >= v2; k -- )
                f[j][k] = max(f[j][k], f[j - v1][k - v2] + 1);
    }

    cout << f[V1][V2 - 1] << ' ';
    int s=0;
    for(int k=0;k<V2;k++)
    {
        if(f[V1][k]==f[V1][V2-1])
        {
            s=k;
            break;
        }
    }
    cout << V2 - s << endl;

    return 0;
}

2.(体力、精灵数为费用，精灵球数为价值) $O(k^2m)$
f[i][j] 表示体力为 i, 收集了 j个 精灵 用的最小的精灵球数量

#include <iostream>
#include <algorithm>
#include <cstring>

using namespace std;

const int INF = 0x3f3f3f3f;
const int N = 110,M=510;
int f[N][M]; // f[i][j] 是捕捉精灵数为i消耗体力值为j消耗的最少的精灵球数
int n, m, k;
int res,ans;

int main()
{
    scanf("%d%d%d",&n,&m,&k);

    memset(f, 0x3f, sizeof f);

    // 初始化, 捕捉精灵数为0消耗的精灵球数肯定为0
    for(int i = 0; i <= m-1 ;  i ++)
        f[0][i] = 0;

    for(int i = 0; i <k; i ++)
    {
        int v1,v2;
        cin >> v1 >> v2;
        for(int j = k; j >= 0; j -- )
        {
            for(int k = m - 1; k >= v2; k --)
            {
                // 精灵球数必须在n之内
                if(f[j - 1][k - v2] + v1 <= n)
                    f[j][k] = min(f[j][k], f[j - 1][k - v2] + v1);
            }
        }
    }

    // 捕捉最大精灵数
    for(int i = k; i >= 0; i --) 
        if(f[i][m - 1] != INF)
        {
            res = i;
            break;
        }

    //满足精灵球数的消耗在n之内，且消耗体力值最小

    for(int i=0;i<m;i++)
        if(f[res][i] <= n)
        {
            ans=i;
            break;
        }
    cout << res << " " << m - ans << endl;

    return 0;
}

acwing1020

初始化为INF还是-INF取决于题目求的是最大值还是最小值

#include <cstring>
#include <iostream>

using namespace std;

const int N = 22, M = 80;

int n, m, K;
int f[N][M];

int main()
{
    cin >> n >> m >> K;

    memset(f, 0x3f, sizeof f);
    f[0][0] = 0;

    while (K -- )
    {
        int v1, v2, w;
        cin >> v1 >> v2 >> w;
        for (int i = n; i >= 0; i -- )
            for (int j = m; j >= 0; j -- )
                f[i][j] = min(f[i][j], f[max(0, i - v1)][max(0, j - v2)] + w);
    }


    cout << f[n][m] << endl;

    return 0;
}

背包问题求方案数

acwing278

#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

const int N = 10010;

int n, m;
int f[N];

int main()
{
    cin >> n >> m;
    f[0] = 1;
    for (int i = 0; i < n; i ++ )
    {
        int v;
        cin >> v;
        for (int j = m; j >= v; j -- ) f[j] += f[j - v];
    }

    cout << f[m] << endl;

    return 0;
}

acwing1021
从前i种物品里选，总体积不超过j的方案数，完全背包

#include <iostream>

using namespace std;

typedef long long LL;

const int M = 3010;

int n, m;
LL f[M];

int main()
{
    cin >> n >> m;

    f[0] = 1;
    for (int i = 0; i < n; i ++ )
    {
        int v;
        cin >> v;
        for (int j = v; j <= m; j ++ )
            f[j] += f[j - v];
    }

    cout << f[m] << endl;

    return 0;
}

acwing
求恰好是最优解方案数。g[i][j]表示只从前i个物品中选体积恰好是j的方案数

#include <cstring>
#include <iostream>

using namespace std;

const int N = 1010, mod = 1e9 + 7;

int n, m;
int f[N], g[N];

int main()
{
    cin >> n >> m;

    memset(f, -0x3f, sizeof f);
    f[0] = 0;
    g[0] = 1;

    for (int i = 0; i < n; i ++ )
    {
        int v, w;
        cin >> v >> w;
        for (int j = m; j >= v; j -- )
        {
            int maxv = max(f[j], f[j - v] + w);
            int s = 0;
            if (f[j] == maxv) s = g[j];
            if (f[j - v] + w == maxv) s = (s + g[j - v]) % mod;
            f[j] = maxv, g[j] = s;
        }
    }

    int res = 0;
    for (int i = 1; i <= m; i ++ )
        if (f[i] > f[res])
            res = i;

    int sum = 0;
    for (int i = 0; i <= m; i ++ )
        if (f[i] == f[res])
            sum = (sum + g[i]) % mod;

    cout << sum << endl;

    return 0;
}

混合背包(https://www.acwing.com/problem/content/7/)

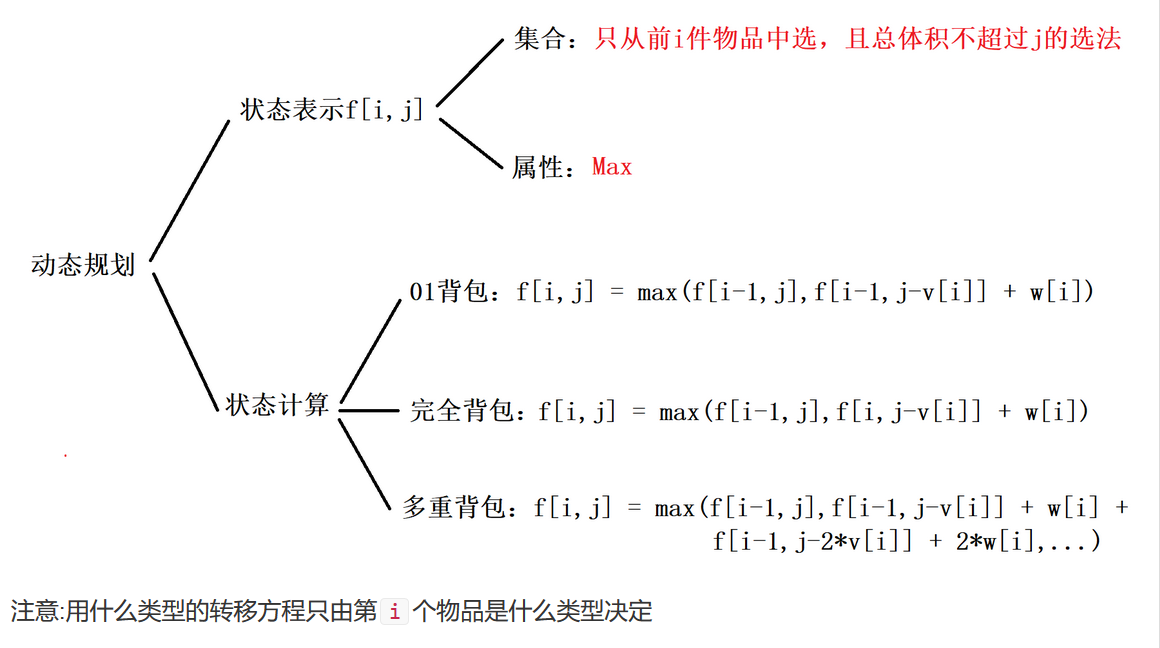
#include <iostream>

using namespace std;

const int N = 1010;

int n, m;
int f[N];

int main()
{
    cin >> n >> m;

    for (int i = 0; i < n; i ++ )
    {
        int v, w, s;
        cin >> v >> w >> s;
        if (!s)
        {
            for (int j = v; j <= m; j ++ )
                f[j] = max(f[j], f[j - v] + w);
        }
        else
        {
            if (s == -1) s = 1;
            for (int k = 1; k <= s; k *= 2)
            {
                for (int j = m; j >= k * v; j -- )
                    f[j] = max(f[j], f[j - k * v] + k * w);
                s -= k;
            }
            if (s)
            {
                for (int j = m; j >= s * v; j -- )
                    f[j] = max(f[j], f[j - s * v] + s * w);
            }
        }
    }

    cout << f[m] << endl;

    return 0;
}

背包问题求具体方案

acwing1013

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 11, M = 16;

int n, m;
int w[N][M];
int f[N][M];
int way[N];

int main()
{
    cin >> n >> m;

    for (int i = 1; i <= n; i ++ )
        for (int j = 1; j <= m; j ++ )
            cin >> w[i][j];

    for (int i = 1; i <= n; i ++ )
        for (int j = 0; j <= m; j ++ )
            for (int k = 0; k <= j; k ++ )
                f[i][j] = max(f[i][j], f[i - 1][j - k] + w[i][k]);

    cout << f[n][m] << endl;

    int j = m;
    for (int i = n; i; i -- )
        for (int k = 0; k <= j; k ++ )
            if (f[i][j] == f[i - 1][j - k] + w[i][k])
            {
                way[i] = k;
                j -= k;
                break;
            }

    for (int i = 1; i <= n; i ++ ) cout << i << ' ' << way[i] << endl;

    return 0;
}

有依赖背包

考虑到所有这些策略都是互斥的（也就是说，你只能选择一种策略），所以一个主
件和它的附件集合实际上对应于分组背包中的一个物品组，每个选择了主件又选择了若干个附
件的策略对应于这个物品组中的一个物品，其费用和价值都是这个策略中的物品的值的
和。但仅仅是这一步转化并不能给出一个好的算法，因为物品组中的物品还是像原问题
的策略一样多。
我们可以想到，对于第 k 个物品组中的
物品，所有费用相同的物品只留一个价值最大的，不影响结果。所以，可以对主件 k 的

acwing10

#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

const int N = 110;

int n, m;
int v[N], w[N];
int h[N], e[N], ne[N], idx;
int f[N][N];

void add(int a, int b)
{
    e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}

void dfs(int u)
{
    for (int i = h[u]; ~i; i = ne[i])
    {
        int son=e[i];
        dfs(son);
        for (int j = m - v[u]; j >= 0; j -- )
            for (int k = 0; k <= j; k ++ )
                f[u][j] = max(f[u][j], f[u][j - k] + f[son][k]);
    }

    for (int j = m; j >= v[u]; j -- ) f[u][j] = f[u][j - v[u]] + w[u];
    for (int j = 0; j < v[u]; j ++ ) f[u][j] = 0;
}

int main()
{
    cin >> n >> m;

    memset(h, -1, sizeof h);
    int root;
    for (int i = 1; i <= n; i ++ )
    {
        int p;
        cin >> v[i] >> w[i] >> p;
        if (p == -1) root = i;
        else add(p,i);
    }

    dfs(root);

    cout << f[root][m] << endl;

    return 0;
}

acwing487
可以将每个主件及其附件看作一个物品组，记主件为 p，两个附件为 a,b，则最多一共有4种组合：
1.p
2.p,a
3.p,b
4.p,a,b
这四种组合是互斥的，最多只能从中选一种，因此可以将每种组合看作一个物品，那么问题就变成了分组背包问题。
在枚举四种组合时可以使用二进制的思想，可以简化代码。

#include <cstring>
#include <iostream>
#include <algorithm>
#include <vector>

#define v first
#define w second

using namespace std;

typedef pair<int, int> PII;

const int N = 60, M = 32010;

int n, m;
PII master[N];
vector<PII> servent[N];
int f[M];

int main()
{
    cin >> m >> n;

    for (int i = 1; i <= n; i ++ )
    {
        int v, p, q;
        cin >> v >> p >> q;
        p *= v;
        if (!q) master[i] = {v, p};
        else servent[q].push_back({v, p});
    }

    for (int i = 1; i <= n; i ++ )
        for (int u = m; u >= 0; u -- )
        {
            for (int j = 0; j < 1 << servent[i].size(); j ++ )
            {
                int v = master[i].v, w = master[i].w;
                for (int k = 0; k < servent[i].size(); k ++ )
                    if (j >> k & 1)
                    {
                        v += servent[i][k].v;
                        w += servent[i][k].w;
                    }
                if (u >= v) f[u] = max(f[u], f[u - v] + w);
            }
    }

    cout << f[m] << endl;

    return 0;
}

本题属于 非树形有依赖的背包问题（只有两类物品：主件，附件），下面给出具体解题思路。

但我们正解的话，可以先对每种主件的 附件的集合 进行一次 010101 背包处理，就可以先求出 对于每一种主件包括其附件的组合中，每种花费的最大价值

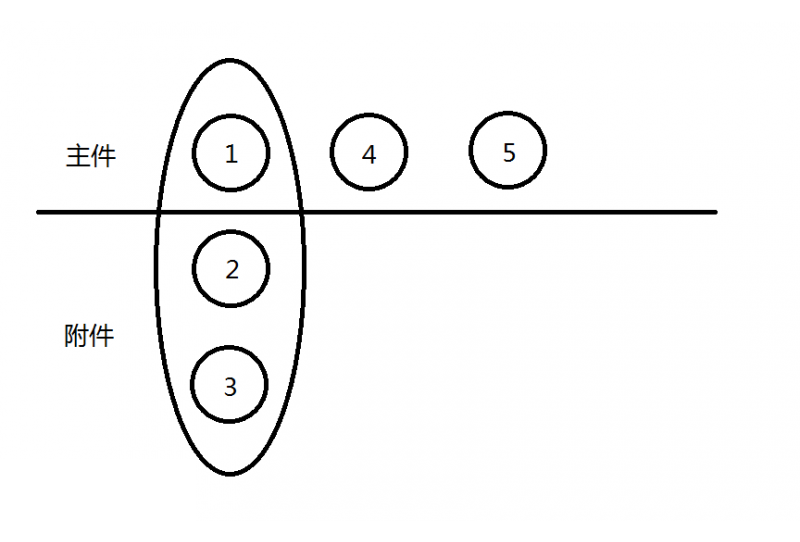
对于每一种主件的01背包处理：

for i：主件k的所有附件
    for j：价值（0 ~ n-主件价值）
        01背包递推

PS ：n为总钱数

推荐博客：
https://blog.csdn.net/yandaoqiusheng/article/details/84782655