欢迎各位AcMer侃侃Eureka的博客

二分图的模样 :

 乱侃一通   ：从字面上来理解,二分图肯定是两部分,既然是两部分那么这两部分肯定各自独立,然后通过一定
             的关系进行建立连接。
 理论上来说 : 如果一张无向图的 N 个节点(N >= 2) 可以被分成 A,B 两个非空集合,其中 A 交 B = 空集,
             并且在同一集合内的点之间都没有边相连,那么这张无向图就是一张二分图,A,B分别称为二分图
             的左部和右部。

看个图:

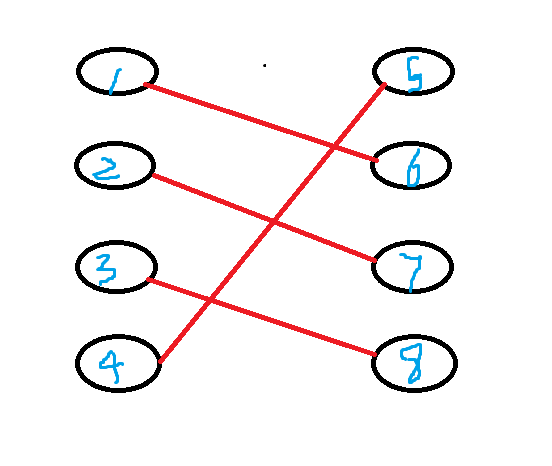
根据上图,我们来侃侃一些概念 :

匹配 : “任意两条边都没有公共端点” 的边的集合被称为图的一组匹配(图中的1 - 6，,2 - 7 )。
最大匹配:包含边数最多的一组被称为二分图的最大匹配 。 (上图的匹配就是最大匹配)

增广路径 : 该算法也被称为增广路算法,每次从左部的点找与右部匹配的点时,我们需要去找一条增广路径,如果
          该路径存在,说明可以将目前的所有点进行匹配，反之则右部则没有与之左部相匹配的点。

增广路 具体讲解可参考这位大佬的博客,解释的比较形象

Code PK Self

#include <cstdio>
#include <string>
#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

const int SIZE = 1e5 + 10;
int match[SIZE],vis[SIZE];                    // match : 存储两个部分之间的匹配关系 vis ： 标记是否访问过某个点
int head[SIZE],ver[SIZE],Next[SIZE];                // 存储两个部分之间的关系

int n1,n2,m,tot;
int u,v;

int main(void) {
    void add(int u,int v);
    bool DFS(int u);
    scanf("%d%d%d",&n1,&n2,&m);
    for(int i = 1; i <= m; i ++) {
        scanf("%d%d",&u,&v);
        add(u,v);
    }
    int res = 0;
    for(int i = 1; i <= n1; i ++) {
        memset(vis,0,sizeof(vis)); // 每次都是从左部一个新的点出发,所以每次都需要进行Clear，我们只需要关注 match 数组即可
        if(DFS(i)) res ++;         // 左部和右部可以匹配的数量 + 1
    }
    cout << res << endl;
    return 0;
}

void add(int u,int v) {
    ver[ ++ tot] = v,Next[tot] = head[u],head[u] = tot;
    return ;
}

bool DFS(int u) {
    for(int i = head[u]; i; i = Next[i]) {
        int y = ver[i];
        if(!vis[y]) {
            vis[y] = 1;
            if(!match[y] || DFS(match[y])) {  
                           // 有可以直接匹配的或者通过找到一条增广路径的匹配点都可以
                match[y] = u;  
                           // 深搜回溯是,正好把路径上的状态取反,就会将所以的边都匹配
                return true;
            }
        }
    }
    return false;     // 与自己相关联的点都已经名花有主了,说明这条路行不通了
}

有不懂得地方,欢迎留言！！！