斜率优化学习笔记

历史记录

清除记录

猜你想搜

AcWing热点
App
登录/注册

斜率优化学习笔记

作者：

Sata_星空 , 2020-02-02 21:45:47 , 所有人可见 , 阅读 1734

N方 D P 要A掉

斜率优化少不了

[HTML_REMOVED]

前言：

$~\\$

$\quad\quad$ 曾经看过斜率优化…当时没有看懂。

$\quad\quad$ 因为 CSP/NOIP 也不用…当时就没怎么在意。

$\quad\quad$ 今天花了半个下午，A掉了斜率优化的板子…写一篇学习笔记加以巩固…

$~\\$

$\quad\quad$ Update（20/06/18）：修复了一些细节错误。

$~\\$

正文：

$\quad\quad$ 下面首先用一道例题引出这个知识点。

例题：洛谷 P3195 [HNOI2008]玩具装箱TOY /【模板】斜率优化

题目大意：把 $n$ 个物品分成若干组，某组中不同物品间要空一个单位长度，物品长度为 $C_i$ ，每一组会带来该组长度 $l$ 与某一固定常数 $L$ 之差的平方的代价。求最小代价和。

$\quad\quad$ 本题 DP 方程显然：设 $f(i)$ 为把前 $i$ 个物品放置好的最小代价，则有

$$f(i)=min((S(j+1,i)+i-j-1-L)^2+f(j))$$

$\quad\quad$ 式子的实际意义是枚举上一个容器的终止节点，其中 $S(i,j)$ 代表 $i - j$ 物品的长度和。

$\quad\quad$ 显然，转移内部的$j$需要从 $0$ 穷举到 $k-1$，总复杂度为$O(n^2)$。

裸 $DP$ 代码（变量名有些不一样）：

for(int k = 1; k <= n; k++)
    for(int i = 0; i < k; i++)
        f[k] = min(f[k], f[i] + (int )pow((cl[k] - cl[i] + k - i - 1 - L, 2));
//cl为C的前缀和

$~\\$

$\quad\quad$ 观察数据规模：$1<=n<=5*10^4 $， $O(n^2)$ 是显然跑不过去的。

$\quad\quad$ 如何优化本题的时间复杂度？外层的$1$~$n$的循环很难优化，考虑从内层循环下手。

$\quad\quad$ 观察 DP 方程里，$min((S(j+1,i)+i-j-1-L)^2+f(j))$ 这一部分似乎和单调队列优化有关。

$\quad\quad$ 单调队列可优化 $f(i)=min(f(j)+X)$ 的过程，但要求 $X$ 是常数，而这里的 $(S(j+1,i)+i-j-1-L)^2$ 显然与 $i$ 有关，所以不能简单当做常数。所以不能使用单调队列优化，但是可以使用斜率优化。

$~\\$

$\quad\quad$ 斜率优化，顾名思义，是通过斜率对 DP 进行优化，与单调队列优化类似，它的优化是针对转移方式的。

$\quad\quad$ 斜率优化的关键在 “斜率”，让我们对 DP 做一些变形：

$$f(i)=min((S(j+1,i)+i-j-1-L)^2+f(j))$$

$\quad\quad$ 我们先把平方打开，打开的过程中可以考虑换元。

$\quad\quad$ 令$A(i)=cl(i)+i,B(j)=cl(j)+j+1+L$。（$cl$ 代表前缀和数组，这里把 $S$ 拆开了）

$\quad\quad$ 这里换元的目的仅仅只是为了好算，没有特定的要求，把 $B[j]$ 里面的常数丢 $A[i]$ 里面也是可以的，换元后的 $A(i),B(j)$ 与 $cl(i),cl(j)$ 类似，仍是关于 $i,j$ 的函数。

$\quad\quad$ 式子变为：

$$f(i) = min(f(j) + (A(i)-B(j))^2)$$

$\quad\quad$ 现在就很好展开了。

$$f(i) = min(f(j) + A(i)^2+B(j)^2-2*A(i)*B(j))$$

$\quad\quad$ 式子中的函数分为两类，一种是可变的，一种是不可变的。

$\quad\quad$ 首先，所有与 $i$ 有关的数值都可以视作不变，因为我们进行内层循环求 $f(i)$ 时，是对于某一个特定的 $i$ 求的。

$\quad\quad$ 剩下来的与 $i$ 有关的式子都会随 $i$ 改变。

$\quad\quad$ 我们不妨去掉 $min$，这个$min$ 的实际意义是：找到一个 $j$ 使得 $f(i)$ 算出来最小，我们只需要找到这个 $j$ 就可以了。

$$f(i) = f(j) + A(i)^2+B(j)^2-2*A(i)*B(j)$$

$\quad\quad$ 我们稍微移一下项$-----$①

$$B(j)^2+f(j)=2*A(i)*B(j)+f(i)-A(i)^2$$

$\quad\quad$ 移项后，等式左边的项都只与 $j$ 有关，等式右边的 $B[j]$ 也与 $i$ 有关，其余的项都是常数。

$\quad\quad$ 我们不妨把 $B(j)$ 看做自变量 $X$ ，把 $B(j)^2+f(j)$ 看做自变量 $Y$ ，认为是 $B(j)$ 的改变造成了 $B(j)^2+f(j)$的改变，现在式子变成这样：

$$Y=2*A(i)*X+f(i)-A(i)^2$$

$\quad\quad$ 观察这个方程，剩下项的都是常数，所以它可以看做一个一次函数，令 $2*A(i)$为斜率 $K$ ，$f(i)-A(i)^2$ 为 $y$ 轴上截距 $B$，有：

$$Y=KX+B$$

$\quad\quad$ （从①开始的移项是有通式的：把既与 $i$ 有关，又与 $j$ 有关的项合并在一起，看做$KX$，把只与 $j$ 有关的项看做 $Y$ ，其他的项看做 $B$）

$\quad\quad$ 对于这个函数，$j$ 的取值是一定的（$1-i-1$），所以 $X,Y$ 的取值也是一定的，这么一来，函数中的 $(X,Y)$ 二元组可以看做坐标系上的定点，如下图。

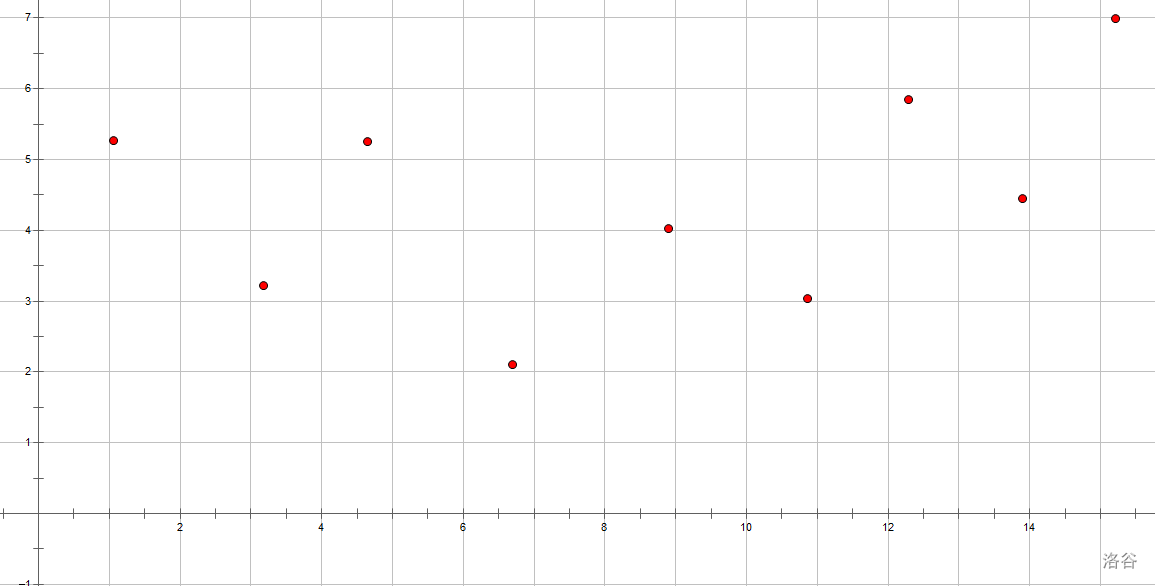
$\quad\quad$ 我们的目的是求出 $f(i)$ 最小值，所以本质上就是求一条斜率恒定（$K=2*A(i)$为定值）的直线，过某个点集中的哪个点，可以获得最小截距（$B=f(i)-A(i)^2,B$ 越小，$f(i)$越小）。

$\quad\quad$ 我们做出一条斜率恒定的直线：

$\quad\quad$ 它必须过点集中的某一点，所以我们将它上移，直到与某个节点相交，那时，它的截距最小，有 $f(i)=Y-KX+A(i)^2$，如下图：

$\quad\quad$ 然而，给我们图我们自然可以求，但怎么让电脑找直线与点群的第一个交点呢？

$\quad\quad$ 首先，我们发现点群中有些点是没必要存在的。

$\quad\quad$ 比如说 $F,E,B$ 点，无论直线斜率为多少，只要是求最小截距，就一定轮不到它们。

$\quad\quad$ 所以我们大可以把它们删掉。

$\quad\quad$ 观察这几个点的共通之处，如下图：

$\quad\quad$ 可能被一条斜率为某个值的直线穿过的点连成了一个凸包，显然，凸包外的点不可能第一个与任意斜率的直线相交（前提是我们要让截距最小）。

$\quad\quad$ 所以，我们不需要维护点集，维护一个下凸包就好。

$\quad\quad$ 而本题中的$X($即$B(j))$显然是递增的，所以可以用单调队列维护凸包，如下图：

$\quad\quad$ 原本 $A,B,C,D$ 构成了凸包，插入了节点 $E$ 以后，凸包被打破…

$\quad\quad$ 组成凸包的线段的斜率需要从左往右递增，所以我们可以从被打破的点（$D$）开始，向左右删不合条件的节点，直到凸包重新出现。（这个删法对于不同的凸包在不同的方向上是不同的，不给通式，建议自己试一试）

$\quad\quad$ 本图中，$C,E$连成的边，与 $A,B$ 构成了新的凸包。

$\quad\quad$ 本题比较特殊，按照我们的思路，跑完出 $f(i)$ 后，我们求 $f(i+1)$ 的过程中可以直接利用 $f(i)$ 的凸包，只需要在上面再加一个点($B(i),B(i)^2+f(i)$)就行了。

$\quad\quad$ 而 $B(i)$ 又是单调的，所以我们只会在凸包的一侧插入节点，删除不合条件的节点也只需要往一侧删就好了。

$\quad\quad$ 但是还有一个问题：对一个凸包而言，什么时候第一次与一条直线相交？

$\quad\quad$ 显然是凸包与直线 $l$ 相切与某个点的时候。

$\quad\quad$ 根据凸包的性质（这里以图中的凸包为例，不同凸包不一定一样），相切的点左边的，构成凸包的所有线段斜率一定小于 $l$ ，右边的直线则一定大于 $l$。

$\quad\quad$ 本题中又很特殊：当我们按从 $1$ 到 $n$ 的顺序求解 $f(i)$ 时，直线的斜率 $K$ 递增。

$\quad\quad$ 所以，我们可以判断凸包最左侧的两点连线 $c$ 斜率是否大于直线 $l$，如果大于，那么切点一定是凸包左端点，否则左端点可以删去（类似单调队列，以后的 $l’$ 斜率一定大于$l$，斜率就一定不会小于 $c$）。

$\quad\quad$ 上面讲的很乱，不过大致把本题斜率优化的操作流程讲了一遍，下面总结具体步骤：

1.求出前缀和等必要的量，换元，把 DP 方程写的尽量简单。

2.确定可以使用斜率优化，画图找该维护的凸包，依次算出要求的DP值，这里又分几个小步骤（这几个小步骤在不同的题中不相同，具体要看方程和凸包，下面只是针对这一道题的步骤）

    首先，把单调队列左边的，以后永远用不上的点删掉。

    然后，取队首节点为直线与凸包切点，算出直线方程，求得f(i)。

    接着，在加入f(i)对应的节点(x,y)前，删掉单调队列右边的，在加入(x,y)后会破坏凸包的点。

    最后，加入点(x,y)。

3.输出f(n)

$~\\’$

$\quad\quad$ 步骤的理由和具体操作，上面基本都有，一些细节可以去代码里找。

$\quad\quad$ 注意：初始时，要把$f(0)=0$（这个初始值对不同的题是不一定相同的）对应的节点放到凸包里面去。

$\quad\quad$ 感觉自己写的不是很清晰，但斜率优化很难弄出一个定式来，它与方程的变量，各变量的单调性息息相关，上面的很多内容都是建立在本题 $XXX$ 有单调性的基础上的，如果没有单调性就会麻烦很多。

代码：

#include <bits/stdc++.h>
#define int long long
//不开long long 见祖宗

using namespace std;

const int N = 50010;

int n, L , C[N] , cl[N] , f[N];

int head = 1, tail = 1, x[N], y[N];

int A(int k)
{
    return cl[k] + k;
}
int B(int k)
{
    return cl[k] + k + 1 + L;
}

//算斜率，不开double都没脸见祖宗
double slope(int a, int b)
{
    return (y[a] - y[b]) / (1.0 * x[a] - x[b]);
}
double slope(int x1, int y1, int x2, int y2)
{
    return (y1 - y2) / (1.0 * x1 - x2);
}

signed main()
{
    scanf("%lld %lld", &n, &L);
    for(int k = 1; k <= n; k++)
        scanf("%lld", &C[k]), cl[k] = cl[k - 1] + C[k];

    x[tail] = B(0), y[tail++] = B(0) * B(0);

    for(int k = 1; k <= n; k++)
    {
        //进格
        while(head + 1 < tail && slope(head, head + 1) < 2 * A(k))
            head++;

        //计算
        f[k] = y[head] - 2 * A(k) * x[head] + A(k) * A(k);
        int new_x = B(k), new_y = f[k] + B(k) * B(k);

        //退格
        while(head + 1 < tail && slope(x[tail - 1], y[tail - 1], new_x, new_y) < slope(tail - 1, tail - 2))
            tail--;

        //填入
        x[tail] = new_x, y[tail++] = new_y;
    }

    printf("%lld", f[n]);

    return 0;
}