前缀和

给定一个序列$a[1-n]$。
有很多次询问，每个询问形如:l r 询问$a[l,r]$的区间和。
每次询问的复杂度要求 O(1)

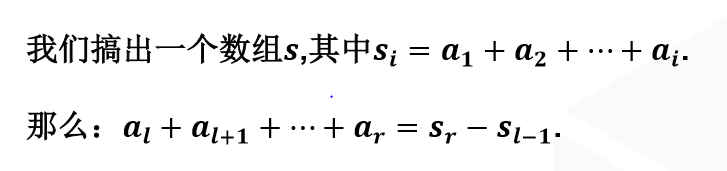
预处理时间复杂度$O(n)$

for(int i=1;i<=n;i++)
{
    scanf("%d",&a[i]);
    s[i]=s[i-1]+a[i];
}

$a[l,r]$的区间和: s[r]-s[l-1]

查询时间复杂度$O(1)$

while(m--)
{
    int l,r;
    scanf("%d%d",&l,&r);
    printf("%d\n",s[r]-s[l-1]);
}

PS:前缀和下标从1开始

区间加/差分

给定一个序列$a[1-n]$(初值全为0)。
有很多次操作，每个操作形如:l r 将$a[l,r]$的每个值加上k。
最后输出整个数组。复杂度要求$O(n)$

区间加[l,r]，实际上是发生了这两件事：
a[l]比前一个元素多了k;
a[r+1]比前一个元素少了k.

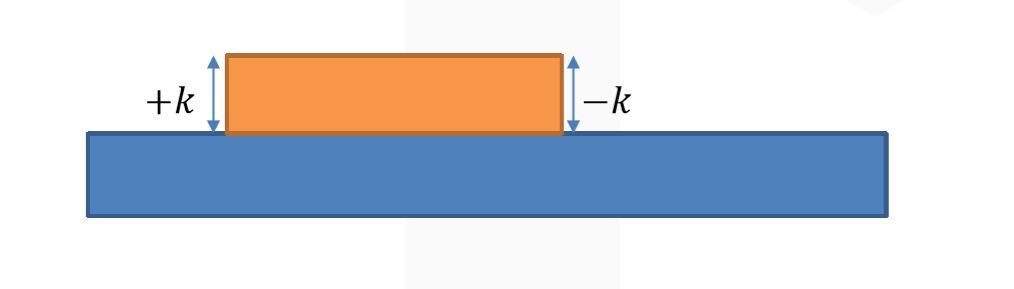
我们用数组b表示刚刚的差值，b[i]=a[i]-a[i-1].
那么：区间加[𝒍,𝒓]，可以化为这两个操作： b[l]+=k; b[r+1]-=k;

void insert(int l,int r,int c)
{
    b[l]+=c;
    b[r+1]-=c;
}

因此，一次区间加只修改这两个元素； 最后利用b数组求出a数组(a数组为b数组的前缀和)，对b数组求一遍前缀和即为答案。

for(int i=1;i<=n;i++)
{
    b[i]+=b[i-1];
    printf("%d ",b[i]);
}

PS:数组a初值为0，进行n次插入操作可得到数组a。

for(int i=1;i<=n;i++)
    scanf("%d",&a[i]);
for(int i=1;i<=n;i++)
    insert(i,i,a[i]);

总结：差分无需构造，前缀和需构造

通过上述的两个方法，我们能轻易地处理这两类问题：
- 数组固定，然后大量询问；
- 大量做区间加，最后要你给出这个数组。

例题

Luogu2879
有好几头牛从１到n线性排列，每头牛的高度为h[i]现在告诉你这里面的牛的最大高 度为maxH,而且有r组关系，每组关系输入两个数字，假设为a和b,表示第a头牛能看到第b头牛，能看到的条件是a, b之间的其它牛的高度都严格小于min(h[a], h[b]),而 h[b] >= h[a] 最后求所有牛的可能最高身高输出

思路：

首先假设所有牛都是最高身高。 读入的约束信息需要去重，这个利用排序或者set可以解决。 可以发现对于每个位置h[i],假设它被覆盖了x次，最后答案就是h[i]-x. 如果出现了一对[l,r]，把区间(l,r)的数都-1就可以了。（注意区间开闭）

#include<iostream>
#include<set> 
using namespace std;
const int N=10010;
int height[N];
set<pair<int,int> > S;

int main()
{
    int n,i,h,r;
    cin>>n>>i>>h>>r;
    height[1]=h;//差分数组 

    while(r--)
    {
        int a,b;
        cin>>a>>b;
        if(a>b)
            swap(a,b);
        if(!S.count({a,b}))
        {
            S.insert({a,b});
            height[a+1]--;
            height[b]++;
        }
    }

    for(int i=1;i<=n;i++)
    {
        height[i]+=height[i-1];
        cout<<height[i]<<endl;
    }
    return 0;
 } 

Luogu3406
该铁路经过N个城市，每个城市都有一个站。不过，由于各个城市之间不能协调好 ，于是乘车每经过两个相邻的城市之间（方向不限），必须单独购买这一小段的车 票。第i段铁路连接了城市i和城市i+1(1<=i<N)。如果搭乘的比较远，需要购买多张 车票。第i段铁路购买纸质单程票需要Ai博艾元。 虽然一些事情没有协调好，各段铁路公司也为了方便乘客，推出了IC卡。对于第i段 铁路，需要花Ci博艾元的工本费购买一张IC卡，然后乘坐这段铁路一次就只要扣 Bi(Bi<Ai)元。IC卡可以提前购买，有钱就可以从网上买得到，而不需要亲自去对应 的城市购买。工本费不能退，也不能购买车票。每张卡都可以充值任意数额。对于 第i段铁路的IC卡，无法乘坐别的铁路的车。 Uim现在需要出差，要去M个城市，从城市P1出发分别按照P1,P2,P3…PM的顺序访 问各个城市，可能会多次访问一个城市，且相邻访问的城市位置不一定相邻，而且 不会是同一个城市。 现在他希望知道，出差结束后，至少会花掉多少的钱，包括购买纸质车票、买卡和 充值的总费用。

直接模拟每段铁路的覆盖即可

 #include<iostream>
using namespace std;
const int N=100010;
 int a[N];
 int b[N];//差分数组 
 typedef long long LL;

 int main()
 {
    int n,m;
    cin>>n>>m;
    for(int i=1;i<=m;i++)
        cin>>a[i];
    for(int i=1;i<m;i++)
    {
        b[min(a[i],a[i+1])]++;
        b[max(a[i],a[i+1])]--;
     }

     for(int i=1;i<=n;i++)
        b[i]+=b[i-1];

//  for(int i=1;i<=n;i++)
//      cout<<"--"<<b[i]<<' ';

    LL sum=0;
    for(int i=1;i<n;i++)
    {
        LL ai,bi,ci;
        cin>>ai>>bi>>ci;
        sum+=min(ai*b[i],ci+bi*b[i]);
    }

    cout<<sum<<endl;
    return 0;
 }

Luogu1083

思路1：

利用差分数组存每天的教室使用情况，然后求前缀和，如果发现不符合要求，就从后往前撤回订单，直到每天都符合要求，那么我们撤回的最后一个（也就是最靠前的一个）即为ans

#include<iostream>
#include<cstdio>
using namespace std;
int n,m;
const int N=1000010,INF=0x3f3f3f3f;
int a[N];
int b[N];
int l[N],r[N],d[N];
int res=INF;

int main()
{
    cin>>n>>m;

    for(int i=1;i<=n;i++)
        scanf("%d",&a[i]);

    for(int i=1;i<=m;i++)
    {
        scanf("%d%d%d",&d[i],&l[i],&r[i]);
        b[l[i]]+=d[i];
        b[r[i]+1]-=d[i];
    }

    int j=m;//从后往前撤回订单，直至满足要求 
    int sum=0;
    for(int i=1;i<=n;i++)
    {
        sum+=b[i];
        //cout<<sum<<' ';
        if(sum>a[i])
        {
            //从后往前撤回 
            while(sum>a[i])
            {
                b[l[j]]-=d[j];
                b[r[j]+1]+=d[j];
                if(i>=l[j] && i<=r[j])
                    sum-=d[j];
                j--;
            }
            res=min(res,j);
        }   
    }

    if(res==INF)
        cout<<"0";
    else 
        cout<<"-1"<<endl<<res+1<<endl;
    return 0;
}

思路2：

在这个题里，因为如果前一份订单都不满足，那么之后的所有订单都不用继续考虑；而如果后一份订单都满足，那么之前的所有订单一定都可以满足，符合局部舍弃性，所以可以二分订单数量。

#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
int n,m;
const int N=1000010,INF=0x3f3f3f3f;
int a[N];
int b[N];
int s[N],t[N],d[N];

bool check(int x)//判断前x份订单能否全部满足 
{
    memset(b,0,sizeof b);
    for(int i=1;i<=x;i++)
    {
        b[s[i]]+=d[i];
        b[t[i]+1]-=d[i];
    }

    for(int i=1;i<=n;i++)
    {
        b[i]+=b[i-1];
        if(b[i]>a[i])
            return false;
    }
    return true;
}

int main()
{
//  freopen("test.in.txt","r",stdin);
//  freopen("test.out","w",stdout);
    scanf("%d%d",&n,&m);

    for(int i=1;i<=n;i++)
        scanf("%d",&a[i]);

    for(int i=1;i<=m;i++)
    {
        scanf("%d%d%d",&d[i],&s[i],&t[i]);
    }
    if(check(m))
    {
        puts("0");
        return 0;
    }
    int l=0,r=m;//l取成0，防止无解情况 
    while(l<r)
    {
        int mid=l+r+1>>1;
        if(check(mid))
            l=mid;
        else    
            r=mid-1;
    }
    cout<<-1<<endl;
    cout<<l+1<<endl;

    return 0;
}

前缀和+差分

luoguP3948

#include<bits/stdc++.h>
using namespace std;
const int N=80010;
typedef long long LL;
LL b[N];
int sum[N];
int n,opt,minn,maxx,l,r,x,f;
LL mod;
char ch[5];

int main()
{
    scanf("%d%d%lld%d%d",&n,&opt,&mod,&minn,&maxx);
    for(int j=1;j<=opt;j++){
        scanf("%s%d%d%",&ch,&l,&r);
        if(ch[0]=='A'){
            scanf("%d",&x);
            b[l]+=x;
            b[r+1]-=x;
        }
        else{
            int ans=0;
            LL now=0;
            for(int i=1;i<=r;i++){
                now+=b[i];
                if(i>=l&&(now*i)%mod>=minn&&(now*i)%mod<=maxx)ans++;
            }
            printf("%d\n",ans);
        }
    }
    scanf("%d",&f);
    for(int i=1;i<=n;i++){
        b[i]+=b[i-1];
        if((b[i]*i)%mod>=minn&&(b[i]*i)%mod<=maxx)sum[i]=sum[i-1]+1;
        else sum[i]=sum[i-1];
    }
    for(int j=1;j<=f;j++){
        scanf("%d%d",&l,&r);
        printf("%d\n",sum[r]-sum[l-1]);
    }
    return 0;
}