本期笔记的内容为背包模型

相关链接：
1.往期笔记： 查看
2.来源：yxc老师的算法提高课

update:

1. 于2020年2月21日 22:08:39更新：增加了背包问题求具体方案与分组背包问题。
2. 于2020年2月23日 21:28:19更新：增加了混合背包问题。

【提高版】DP知识笔记2 有猷 编

各种背包问题的区别：
1. 01背包问题：每种物品选或不选两种情况；
2. 完全背包问题：每种物品选$0\dots\infty$个；
3. 多重背包问题：每种物品选$0\dots s_i$个；
4. 分组背包问题：每组物品选一个。

例题：

1. 01背包问题

思路：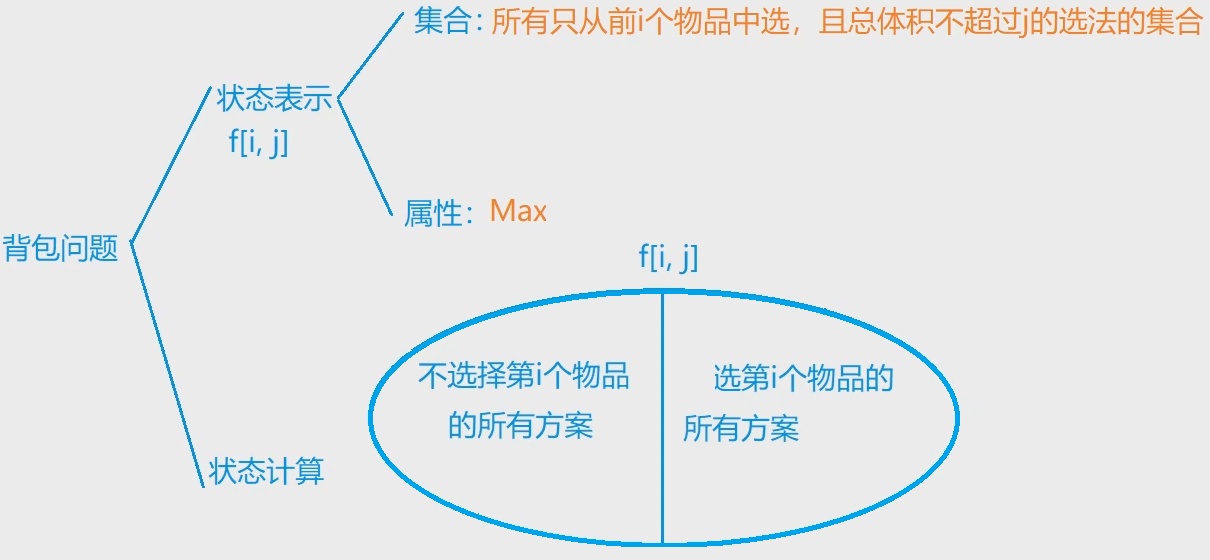
拓展： 二维费用的背包问题
思路：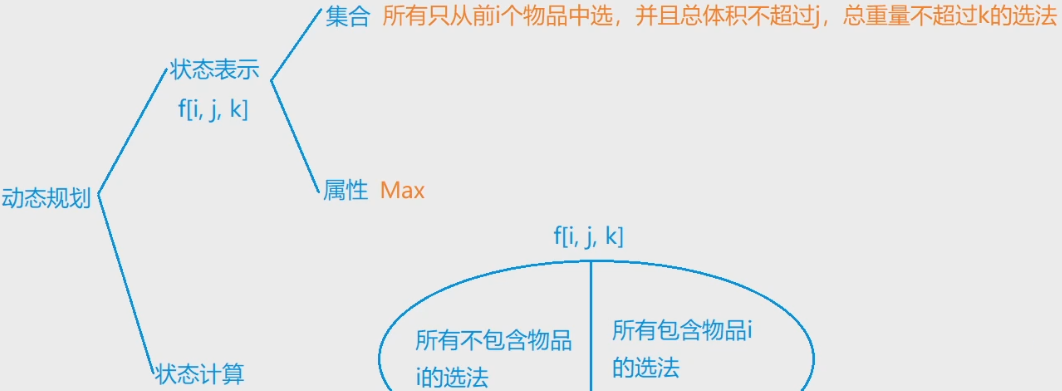

2. 完全背包问题

思路：与01背包问题大致相同，唯一的区别是状态计算

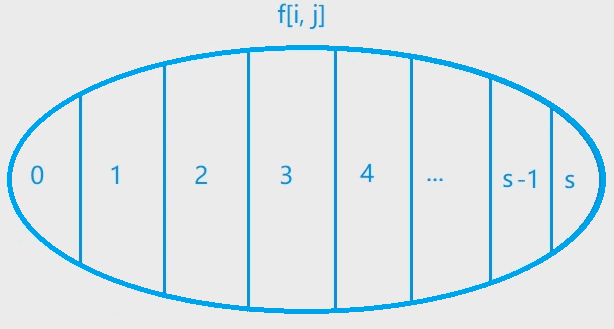
优化：
横向 观察状态转移方程：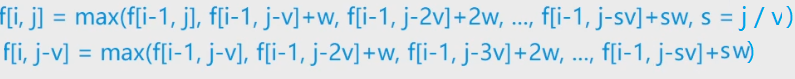
对比：
优化的状态转移方程：f[i][j] = max(f[i - 1][j],f[i][j - v] + w)
结果：状态转移从线性优化成了$O(1)$！
注意，多重背包问题不可以这样优化！（每个物品的$s$值是固定的，状态转移方程会多出一项，无法求解）

3. 多重背包问题

思路：类似于完全背包问题
优化：单调队列优化，纵向 观察状态转移方程，得出：

转化为了滑动窗口求最值问题。
每一项都要加上偏移量$w$。

4. 分组背包问题

思路：与多重背包问题类似。状态转移方程：opt[i][j] = max(opt[i][j],opt[i - 1][j - cost[i][k]] + val[i][k]);

5. 背包问题求具体方案

思路：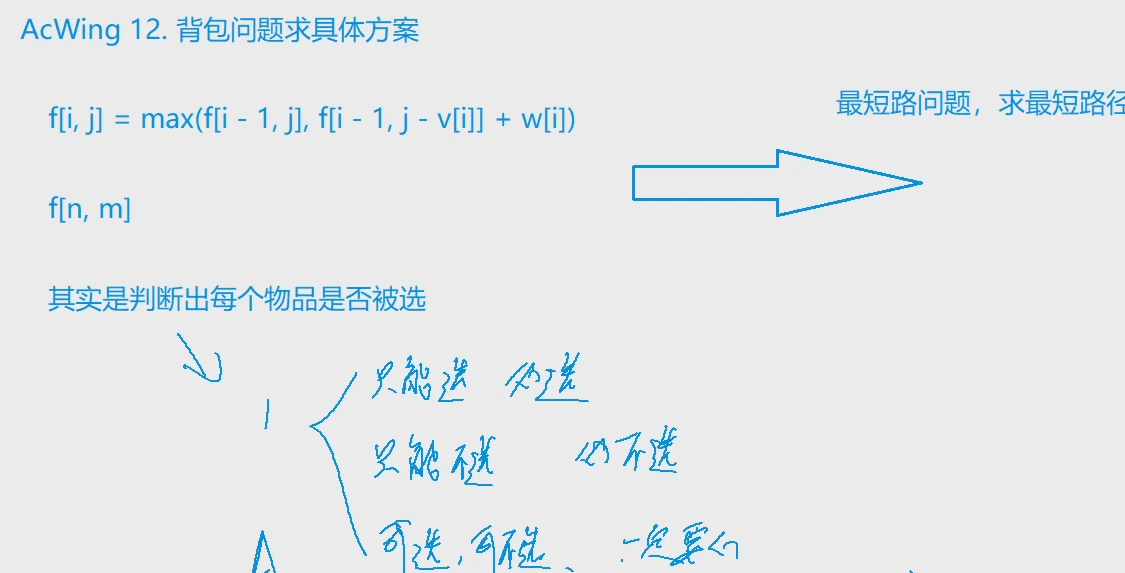

6. 混合背包问题

思路：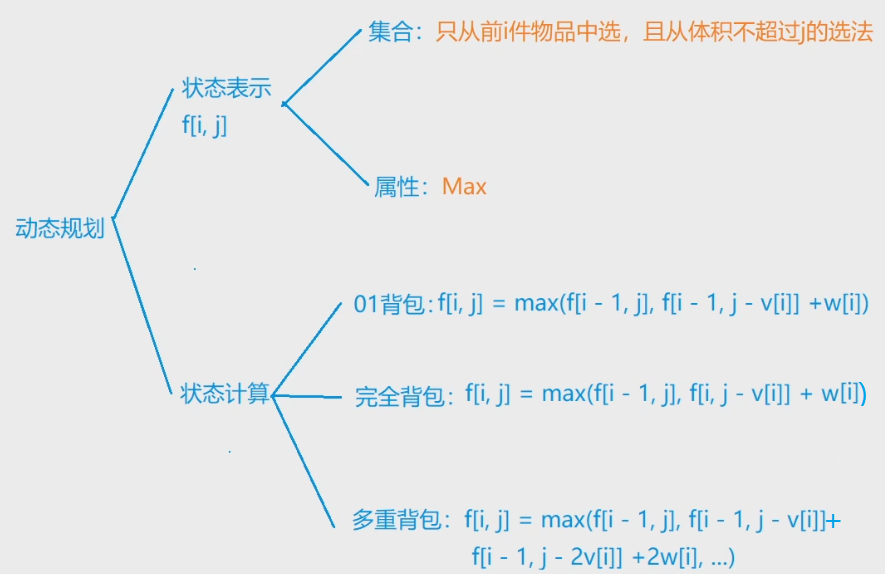

总结：背包问题代码模板：

for(物品){
    for(体积){
        for(决策){
            状态转移方程;
        }
    }
}