最短路概览
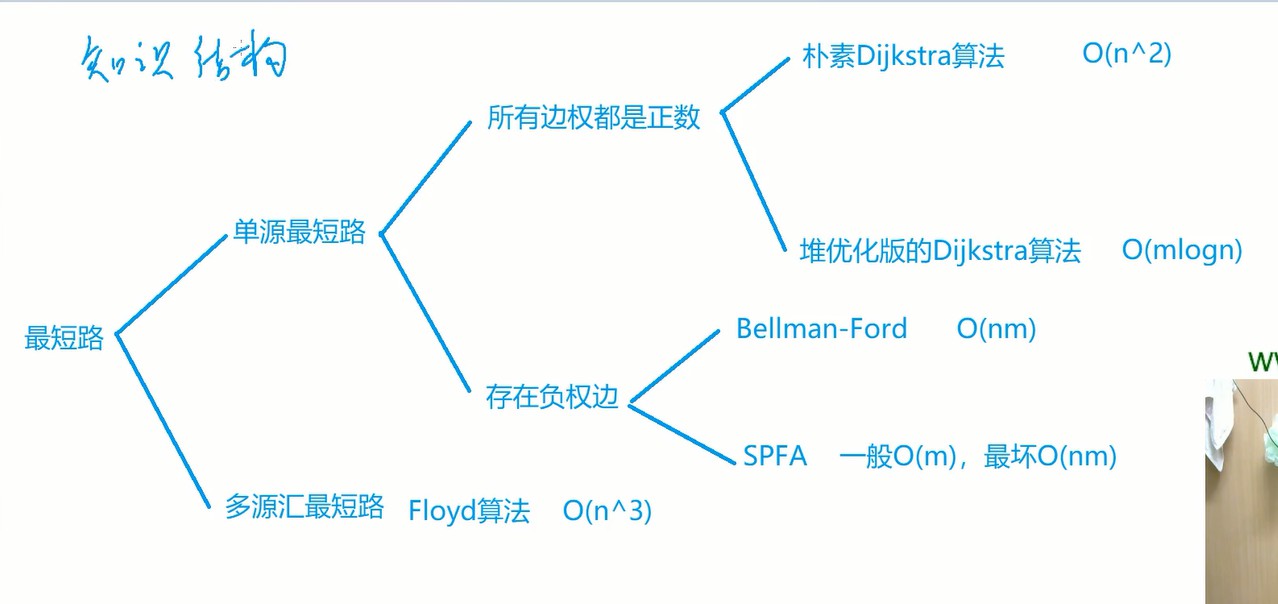
| 算法 | 时间复杂度 | 存储结构 | 备注 |
|---|---|---|---|
| 朴素版dijkstra算法 | $ O(n^2) $ | 邻接矩阵 | 稠密图 n * n ~= m |
| 堆优化版dijkstra | $ O(mlogn) $ | 邻接表 | 邻接表记得初始化头结点 |
| bellman_ford算法 | $ O(nm) $ | 结构体 | 不超过k条边 |
| spfa算法 | 平均$O(m)$,最坏$O(nm)$ | 邻接表 | 邻接表记得初始化头结点 |
| flyod算法 | $ O(n^3) $ | 二维数组 | 多源汇 |
一些感受:
- 感觉spfa算法比较万金油,可以搞定负权边,也可以过dijkstra题目,首选spfa,但可能会被卡(暂时还没遇到过),这时候就要会写dijkstra算法.
- 对于一些特定条件下的算法:
- 不超过k条边:bellman_ford算法
- 多源汇:flyod算法
- 求负环:spfa算法
- 无向图记得建两条边,边数开2倍
朴素版dijkstra算法 AcWing 849. Dijkstra求最短路 I
算法思路:
循环n轮:
1. 找到还没有加入s中且距离原点最近的点
2. 用这个点去更新与之相邻的点
-
时间复杂度分析:循环n轮,找点,更新边,其实是 $O(n^2+m)$,但因为是稠密图 n * n ~= m ,简记为$O(n^2)$
-
代码实现:
#include <iostream>
#include <cstring>
#include <algorithm>
#include <cstdio>
using namespace std;
const int N = 510;
int n,m;
int g[N][N]; // 稠密图(n*n ~= m) 用邻接矩阵来存
int dist[N]; // 各个点到起点的距离
bool st[N];
int dijkstra()
{
memset(dist,0x3f,sizeof dist); // 初始化距离
dist[1]=0; // 初始化起点
for(int i=0;i<n;i++) // 循环n轮(n-1也可,最后一轮不影响)
{
int t=-1;
for(int j=1;j<=n;j++)
if(!st[j] && (t==-1 || dist[j]<dist[t])) // 1.找到还没有加入s中且距离原点最近的点
t=j;
st[t]=true;
for(int j=1;j<=n;j++)
dist[j]=min(dist[j],dist[t] + g[t][j]); // 2.用这个点去更新其他点
}
if(dist[n] == 0x3f3f3f3f) return -1;
return dist[n];
}
int main()
{
scanf("%d%d",&n,&m);
memset(g,0x3f,sizeof g);
while(m--)
{
int a,b,c;
scanf("%d%d%d",&a,&b,&c); // 自环一定不会出现在最短路中
g[a][b]=min(g[a][b],c); // 处理重边:取边权最小的一条即可
}
int t=dijkstra();
printf("%d\n",t);
return 0;
}
堆优化版dijkstra算法 AcWing 850. Dijkstra求最短路 II
算法思路:
循环n轮:
1. 找到还没有加入s中且距离原点最近的点(这一步可用堆优化)
2. 用这个点去更新与之相邻的点
-
时间复杂度分析:最多m条边入堆,找点$logn$, $O(mlogn)$
-
代码实现:
#include <cstring>
#include <algorithm>
#include <queue>
#include <iostream>
using namespace std;
typedef pair<int,int> PII;
const int N = 1e5 + 10;
int n,m;
int h[N],w[N],e[N],ne[N],idx; // 稀疏图,用邻接表来存
int dist[N];
bool st[N];
void add(int a,int b,int c)
{
e[idx]=b,w[idx]=c,ne[idx]=h[a],h[a]= idx ++ ;
}
int dijkstra()
{
memset(dist,0x3f,sizeof dist); // 初始化距离
dist[1]=0;
priority_queue<PII, vector<PII>, greater<PII> > heap; // 定义小根堆
heap.push({0,1}); // <距离,编号>
while(heap.size())
{
auto t=heap.top(); // 优化体现在这里:朴素版是找出还未加入s且距离最近的点
heap.pop(); // 找到距离最近 可用堆
int ver=t.second, distance = t.first;
if(st[ver]) continue;
st[ver] = true;
for(int i=h[ver];i!=-1;i=ne[i]) // 用这个点更新其它点
{
int j=e[i];
if(dist[j] > distance + w[i])
{
dist[j]=distance + w[i];
heap.push({dist[j],j});
}
}
}
if(dist[n]== 0x3f3f3f3f) return -1;
return dist[n];
}
int main()
{
scanf("%d%d",&n,&m);
memset(h,-1,sizeof h); // 初始化表头
while(m--)
{
int a,b,c;
scanf("%d%d%d",&a,&b,&c);
add(a,b,c);
}
cout<< dijkstra()<<endl;
return 0;
}
以下算法原理不是很理解,留待日后学习!
Bellman-Ford算法 853.有边数限制的最短路
算法思路:
循环k次(不超过k条边),每次对所有边做松弛操作(我也不知道松弛操作是什么~~)
-
时间复杂度分析:最多n次迭代,每次对所有边m ,$O(nm)$
-
代码实现:
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 510, M = 10010;
struct Edge{
int a,b,c;
}edges[M];
int n,m,k;
int dist[N];
int last[N]; // 备份
void bellman_ford()
{
memset(dist,0x3f,sizeof dist);
dist[1]=0;
for(int i=0;i<k;i++) // 1. 循环k次
{
memcpy(last,dist,sizeof dist);
for(int j=0;j<m;j++) // 2.对于所有边更新,松弛
{
auto e= edges[j];
dist[e.b]=min(dist[e.b],last[e.a]+e.c); // 这里是备份,注意!
}
}
}
int main()
{
cin>>n>>m>>k;
for(int i=0;i<=m;i++)
{
int a,b,c;
cin>>a>>b>>c;
edges[i]={a,b,c};
}
bellman_ford();
if(dist[n] > 0x3f3f3f3f / 2) puts("impossible"); // 松弛操作也可能更新一点
else cout<<dist[n];
return 0;
}
spfa算法 851. spfa求最短路
算法思路:
循环k次(不超过k条边),每次对所有边做松弛操作(这一步优化:只需对前驱改变的点做松弛操作)
-
时间复杂度分析:平均$O(m)$,最坏$O(nm)$
-
代码实现:
#include <cstring>
#include <algorithm>
#include <queue>
#include <iostream>
using namespace std;
const int N = 100010;
int n,m;
int h[N],w[N],e[N],ne[N],idx;
int dist[N];
bool st[N];
void add(int a,int b,int c)
{
e[idx]=b,w[idx]=c,ne[idx]=h[a],h[a]=idx ++ ;
}
int spfa()
{
memset(dist,0x3f,sizeof dist); // 初始化距离
dist[1]=0; // 先把起点赋上
queue<int> q;
q.push(1);
st[1]=true;
while(q.size()) // 只需要对前驱改变的点做松弛操作
{
int t=q.front();
q.pop();
st[t]=false; // 出队为false
for(int i = h[t];i != -1; i = ne[i])
{
int j=e[i];
if(dist[j] > dist[t] + w[i])
{
dist[j] = dist[t] + w[i];
if(!st[j]) // 避免重复入队
{
q.push(j);
st[j]=true;
}
}
}
}
return dist[n];
}
int main()
{
cin>>n>>m;
memset(h,-1,sizeof h); // 邻接表记得要初始化表头
while(m--)
{
int a,b,c;
cin>>a>>b>>c;
add(a,b,c);
}
if(spfa() == 0x3f3f3f3f) puts("impossible"); // 因为只对前驱改变的点做松弛操作,所以不连通的直接==
else cout<<dist[n]; // 与bellman_ford算法区别
return 0;
}
floyd算法 854. Floyd求最短路
算法思路:
基于动态规划,三重循环,k为阶段(不懂~~)
-
时间复杂度分析:$O(n^3)$
-
代码实现:
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 210 , INF = 1e9;
int n,m,Q;
int d[N][N];
// 算法结束后,d[a][b]表示a到b的最短距离
void floyd()
{
for(int k=1;k<=n;k++)
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
d[i][j]=min(d[i][j],d[i][k]+d[k][j]);
}
int main()
{
cin>>n>>m>>Q;
//初始化
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
if(i==j) d[i][j]=0;
else d[i][j]=INF;
while(m--)
{
int a,b,c;
cin>>a>>b>>c;
d[a][b]=min(d[a][b],c);
}
floyd();
while(Q--)
{
int a,b;
cin>>a>>b;
int t=d[a][b];
if(t > INF/2) puts("impossible"); // 会更新一点,同bellman_ford算法
else cout<<t<<endl;
}
return 0;
}


Orz 正好想着自己总结这些小点呢 你这篇完全覆盖了
发现第一遍学的时候最认真,幸好自己总结了,很快就找回来了。
AcWing 1129. 热浪可以用spfa呀,没有卡
哦,对的,已修改,谢谢。
吓得我翻了翻昨晚写的超时记录,原来是边数没有开2倍,写蒙了hh
hh,加油