概述
我们先来看一张有趣的动图:
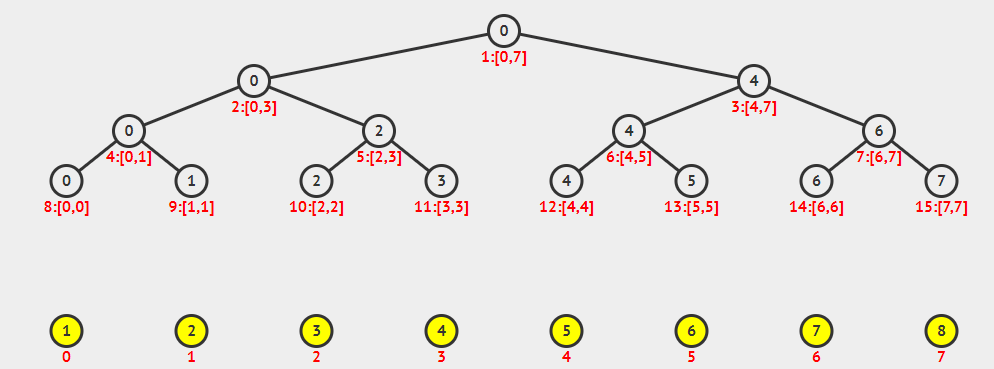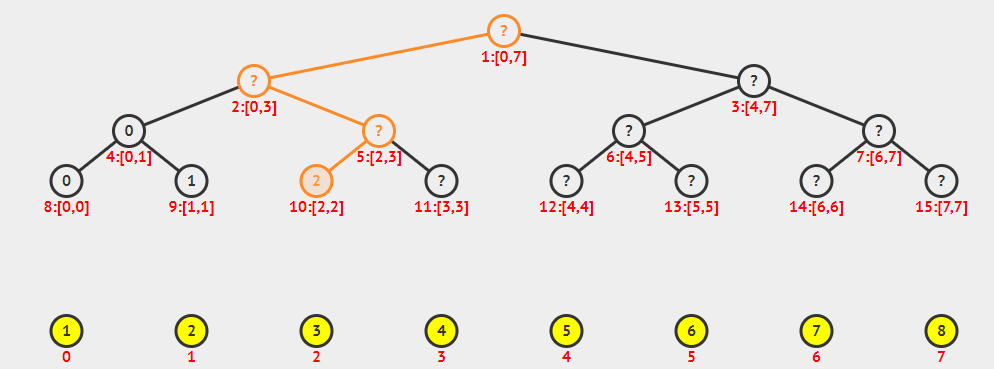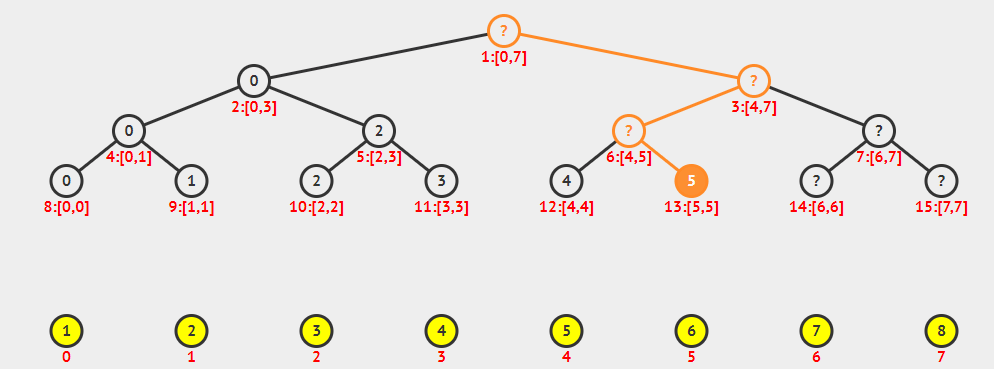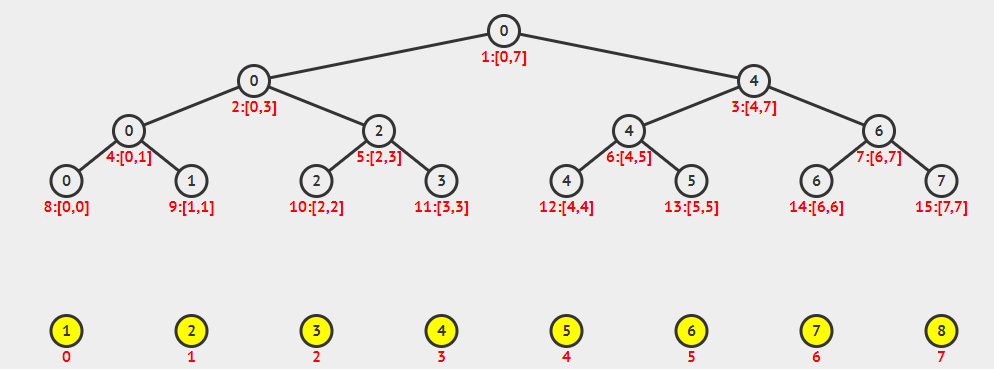
(感谢秦dalao)
- 1.1 有时我们会遇见这样的问题:N个大佬,编号1到N,用A[1],A[2],A[N]表示他们的智商。然后让我们统计:
1.编号从L到R的大佬智商之和为多少?
2.将第L个大佬增加C的智商,然后求和?
其中1<= L <= R <= N.
一般我们会想到两个异常简单的解决方法:
2.1 方法一(暴力):对于统计L,R ,需要求下标从L到R的所有数的和,从L到R的所有下标记做[L..R],问题就是对A[L..R]进行求和。这样求和,对于每个询问,需要将(R-L+1)个数相加。
2.2 方法二(前缀和和差分的思想):更快的方法是求前缀和,令 S[0]=0, S[k]=A[1..k] ,那么,A[L..R]的和就等于S[R]-S[L-1],这样,对于每个询问,就只需要做一次减法,大大提高效率。
我们可以分析一下这两个算法的时间复杂度,都是修改:O(1) O(n),求和: O(n) O(1),小声bb:这个时间复杂度我简易化了,我们可以看出他们的优劣,但是如果我们题目卡时间,那么我们就要寻找一个这两个需求都快的方法:线段树或者树状数组(树状数组将会在系列二中分享)
什么是线段树
基础
- 2.1 基础知识
线段树,是一种二叉搜索树。它将一段区间划分为若干单位区间,每一个节点都储存着一个区间。它功能强大,支持区间求和,区间最大值,区间修改,单点修改等操作。- 2.2 线段树的思想
和分治思想很相像,线段树的每一个节点都储存着一段区间[L…R]的信息,其中叶子节点L=R。它的大致思想是:将一段大区间平均地划分成2个小区间,每一个小区间都再平均分成2个更小区间……以此类推,直到每一个区间的L等于R(这样这个区间仅包含一个节点的信息,无法被划分)。通过对这些区间进行修改、查询,来实现对大区间的修改、查询。- 2.3 时间复杂度
一个包含n个区间的线段树,空间复杂度O(n),查询的时间复杂度则为O(log(n+k)),其中k是符合条件的区间数量。
原理解读
为了防止文字过多,下面我们来看一下张图
总结一下:
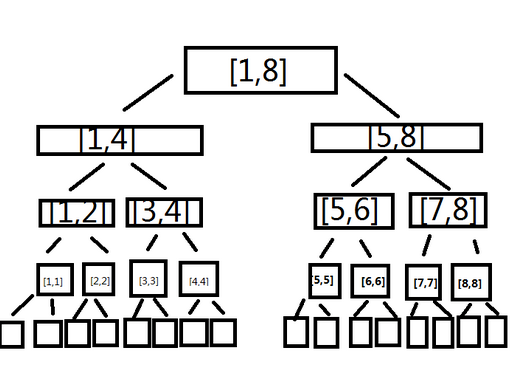
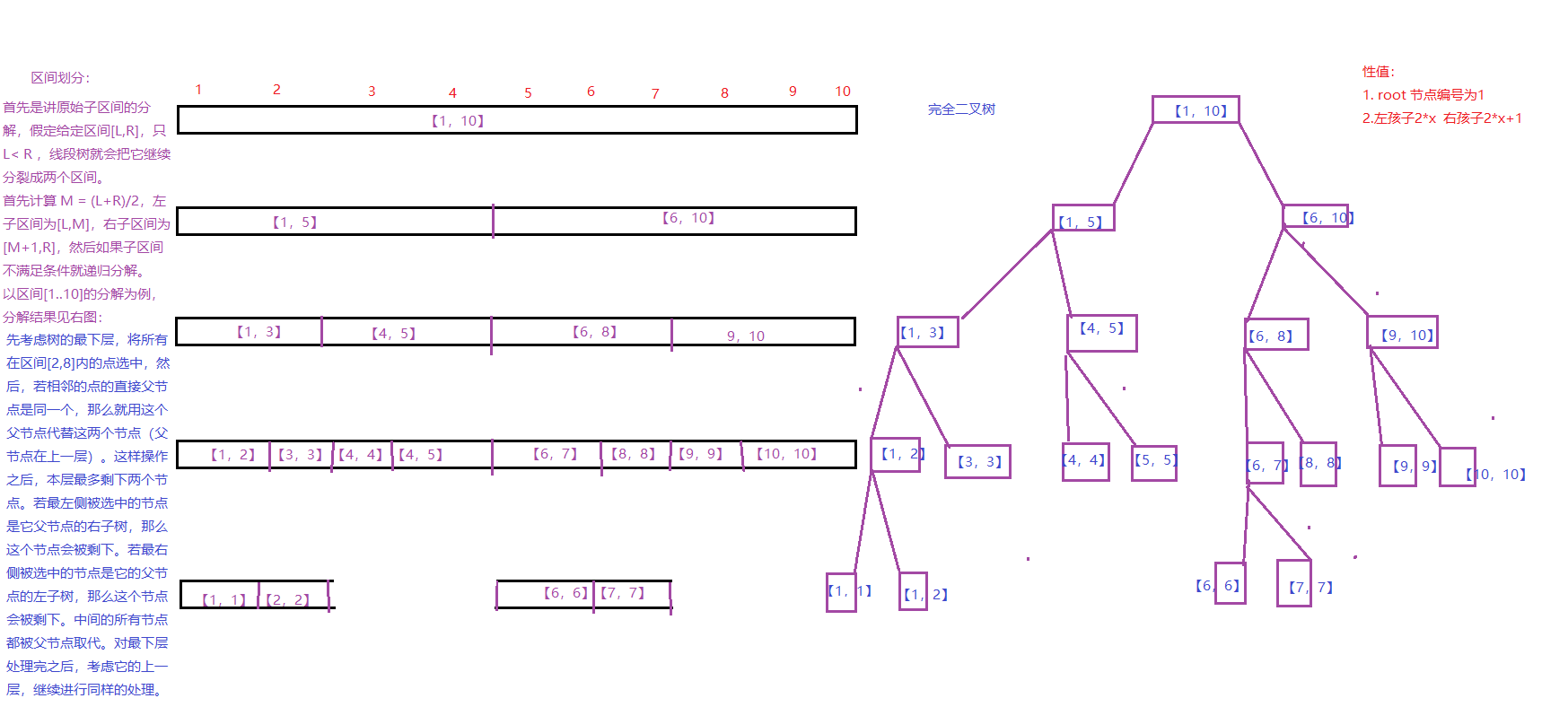
线段树主要是把一段大区间平均地划分成两段小区间进行维护,再用小区间的值来更新大区间。这样既能保证正确性,又能使时间保持在log级别(因为这棵线段树是平衡的)。也就是说,一个[L,R]的区间会被划分成[L,(L+R)/2]和[(L+R)/2+1,R]这两个小区间进行维护,直到L=R。
上图就是一棵[1,10]的线段树的分解过程(相同颜色的节点在同一层)
通常用的都是堆式储存法,即编号为k的节点的左儿子编号为k∗2,右儿子编号为k∗2+1,父节点编号为k/2,用位运算优化一下,以上的节点编号就变成了k<<1,k<<1∣1
通常,每一个线段树上的节点储存的都是这几个变量:区间左边界,区间右边界,区间的答案(这里为区间元素之和)
注意:线段树的大小其实是4n左右的。
- 证明
当然树最后一层节点不完整,有二叉树性质我们可以知道N叶个节点有2N-1,不知道二叉树性质, 请点我 由于在这种存储方式下,最后一层产生了空余,所以我们存储线段树一般数组长度一般不小于4N,保证它不会越界。
线段树定义
struct Node
{
int l/*区间左边界*/;
int r/*区间右边界*/;
int dat/*区间最大值*/;
int sum/*区间元素之和*/;
int lazy/*懒惰标记,下文会提到*/;
Node(){l=r=sum=lazy=0;}//给每一个元素赋初值
}tr[4*N];//N为总节点数
inline void update(int k)//更新节点k的sum
{
tr[k].sum=tr[k*2].sum+tr[k*2+1].sum;
//很显然,一段区间的元素和等于它的子区间的元素和
//如果有懒惰标记的话要相应地改变
}
inline void pushup(int k)//更新节点k的dat
{
tr[k].dat= max(tr[k2].dat, tr[k2+1].dat);
//很显然,一段区间的最大值等于它的子区间的最大值比较
//如果有懒惰标记的话要相应地改变
}
线段树操纵详解
建树并保持区间最大值
存储做好了,我们就开始建树。
我们运用递归的思路来建树。
根据线段树的定义,我们可以递归地将区间[l,r]分成[l,l+r/2]和[l+r/2+1,r]两个子区间,再递归地分下去,直到分成了一个一个的单位区间。
假如我们要对8个数据进行管理,我们就要建立一个线段树。建立的线段树是一个完全二叉树,我们需要借助一个二叉树的性质:
父亲的区间是[a,b],(c=(a+b)/2)左儿子的区间是[a,c],右儿子的区间是[c+1,b],所以线段树需要的空间为数组大小的四倍。
函数声明(我们需要根节点,左右两个儿子),如果到底了,本节点就等于要记载的数组的节点并返回,这也是递归的边界条件,接下来利用性质构筑左右子树mid=(left+right)/2;build(2root,left,mid);build(2root+1,mid+1,right),递归完成后,父节点更新。
void build(int p,int l,int r){
tr[p].l=l,tr[p].r=r;//所在区间
if(l==r){tr[p].dat=a[l];return;}//叶节点
int mid=(l+r)>>1; //折半
build(p*2,l,mid),build(2*p+1,mid+1,r);//创建左右子树
pushup(p);//由下而上更新信息
}
build(1,1,n)// 我们就得到了一棵空的线段树,接下来就是遍历。
单点更新
现在树已经建立完毕,但这还是刚刚开始的存图环节,假如说现在我们要使一个节点更新,比如让第三个数所对应的a[3]+5,会产生“牵一发而动全身”的效应,所以们们需要对它上面的节点再次更新。
假如a[1~8]为 4,6,8,9,3,1,4,7 如图所示:
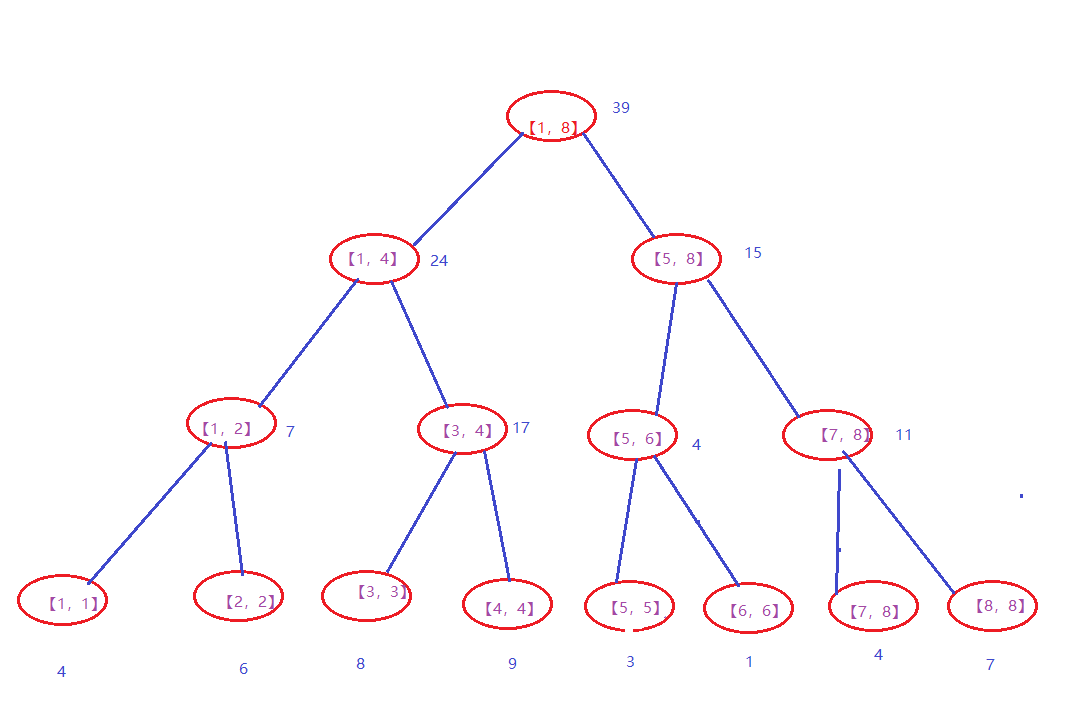
如果我们要给a[2]+9,如下图:
橙色代表区间最大值
所以我们需要对每一个节点更新,使用的数据有本次的根节点,要控制的总范围区间(左,右),要修改的点和要修改的数据。持续更新它的父节点直到顶端即可。
时间复杂度为O(logN)
示例代码:
void change(int p,int x,int v){
if(tr[p].l==tr[p].r){ //找到叶节点
tr[p].dat=v;
tr[p].sum=v;
return;
}
int mid=(tr[p].l+tr[p].r)>>1;
if(x<=mid)change(p*2,x,v); //x属于左边
else change(2*p+1,x,v);//x 属于右边
update(p);
pushup(p);
}
change(1,x,v) //调用入口
区间修改
其实如果会了单点修改的话,区间修改就不会太难理解了。
区间修改大体可以分为两步:
- 找到区间中全部都是要修改的点的线段树中的区间
- 修改这一段区间的所有点
先来解决第一步:
我们先从根节点出发(根节点一定包含所有的点,包括被修改区间),一直往下走,直到当前区间中的元素全部都是被修改元素。
- 当左区间包含整个被修改区间时,我们就递归到左区间;
- 当右区间包含整个被修改区间时,我们就递归到右区间;
否则,情况一定就如下图所示:

怎么办?这种情况似乎有些难了。
不过,通过思考,我们可以发现,被修改区间中的元素间,两两之间都不会产生影响。
所以,我们可以把被修改区间分解成两段,使得其中的一段完全在左区间,另一端完全在右区间。
很明显,直接在mid的位置将该区间切开是最好的。如下图所示:
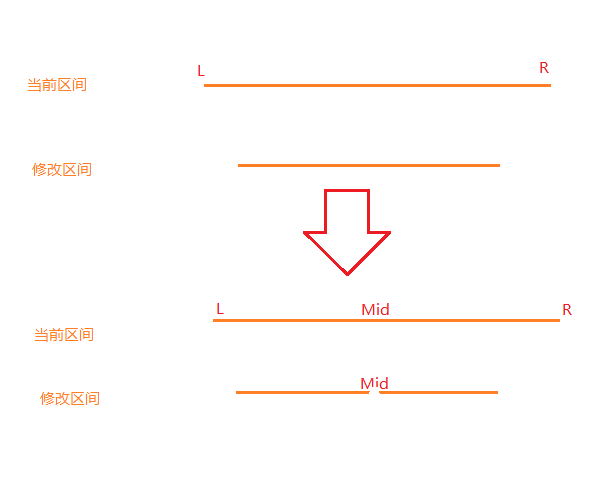
通过一系列的玄学操作,我们成功地把修改区间分解成一段一段的。但问题来了:我们怎样修改这些区间呢?
最暴力的做法是每一次都像建树一样,遍历区间内的所有节点,一一修改。但是这样的时间复杂度显然比暴力还多了个4~5的常数,我要这线段树有何用?
这里就要引入一样新的神奇的东西——延迟标记!
延迟标记
区间更新是个大问题,很多同学会想到用一个for循环,每个点走一遍。虽说思维难度不大,而且在点与点范围跳跃速度也不慢,但当要修改的数据到达一定规模时,这样重复的操作显得累赘而消耗巨量时间,非常容易TLE。所以我们需要找到之间重复的规律,简化程序,以减少不必要的时间浪费。
于是我们想到了一个方法,引入一个延迟标记。原理是在要修改的区间(有时候是全部,有时候是中间的一部分被完全包括),在不使用它的子孙时,暂且将数据扣留下来,于父亲产生影响,并施加一个延迟标记。有了整个关键方法,我们可以建立一个更新函数,首先先判断它的边界问题,
含义:本区间已经被更新过了,但是子区间却没有被更新过,被更新的信息是什么(区间求和只用记录有没有被访问过,而区间加减乘除等多种操作的问题则要记录进行的是哪一种操作)
这里再引入两个很重要的东西:相对标记和绝对标记。相对标记指的是可以共存的标记,且打标记的顺序与答案无关,即标记可以叠加。 比如说给一段区间中的所有数字都+a,我们就可以把标记叠加一下,比如上一次打了一个+1的标记,这一次要给这一段区间+2,那么就把+1的标记变成+3。
绝对标记是指不可以共存的标记,每一次都要先把标记下传,再给当前节点打上新的标记。这些标记不能改变次序,否则会出错。 比如说给一段区间的数字重新赋值,或是给一段区间进行多种操作。
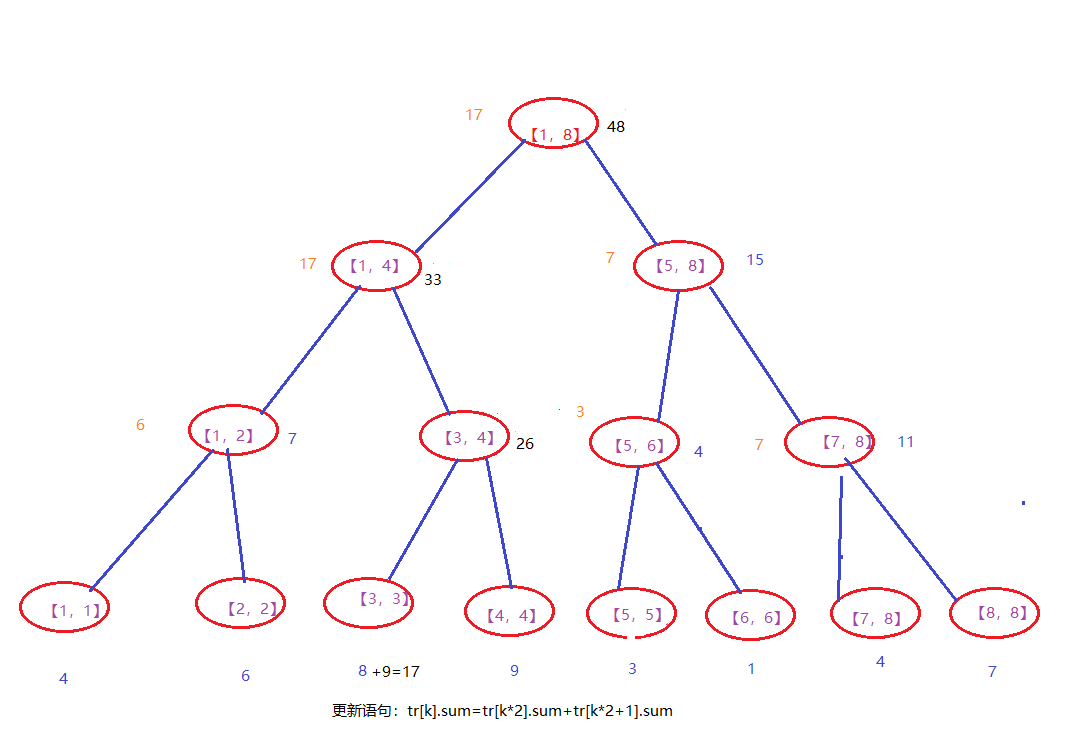
举个栗子,还是那个图,我们假如说要将a[2-5]都要加上5,如下图所示,
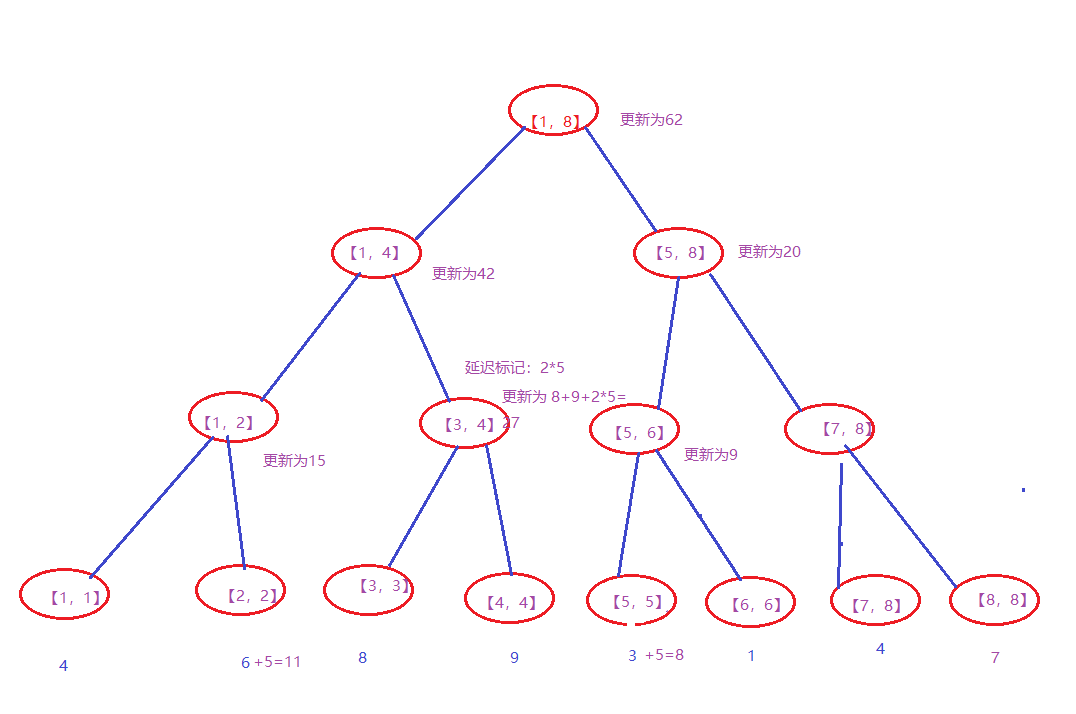
我们首先将其与[1,8]进行比较,发现所更改范围在【1,8】之内,我们往下搜索左右子树,发现【1,4】和【5,8】之中都有。先看【1,4】,先搜索它的左子树【1,2】,发现只有2需要,1不需要,所以直接让右子树2所对应的值8+5,返回,返回,至【1,4】。再看右子树【3,4】,发现这全都在更改的范围之内,所以我们在这里加入一个延迟标记并且【3,4】它本身获得它的子树那么多的增加,将扣押下来的值存储在延迟标记,需要的时候再将其放下。然后再看右子树【5,8】,然后引导至【5,6】,【6,6】直接+5就可以了。
在我们具体来解释一下延迟标记的原理,提需要接收的信息有本次根节点和左右子树。这是一个更新的例行检查,加入一判定这里有延迟标记,便会产生释放,将数据变动载入真实数组。我们意识到一个严重的问题:假如说产生了多组延迟标记,甚至运算符号不同,这样就会陷入巨大的混乱。说是多次加减,或多次乘除,可直接对延迟标记进行操作。但是假如为加减乘除混合运算,恐怕难以清晰实现。
依个人愚见,有两种办法:
- 1、当标记种类较少时,可进行种类判定
- 2、当过于复杂时,不必多种标记分类,不如返璞归真,将上一次标记释放之后在进行新一次的标记。
再来一个新的栗子,如下图:
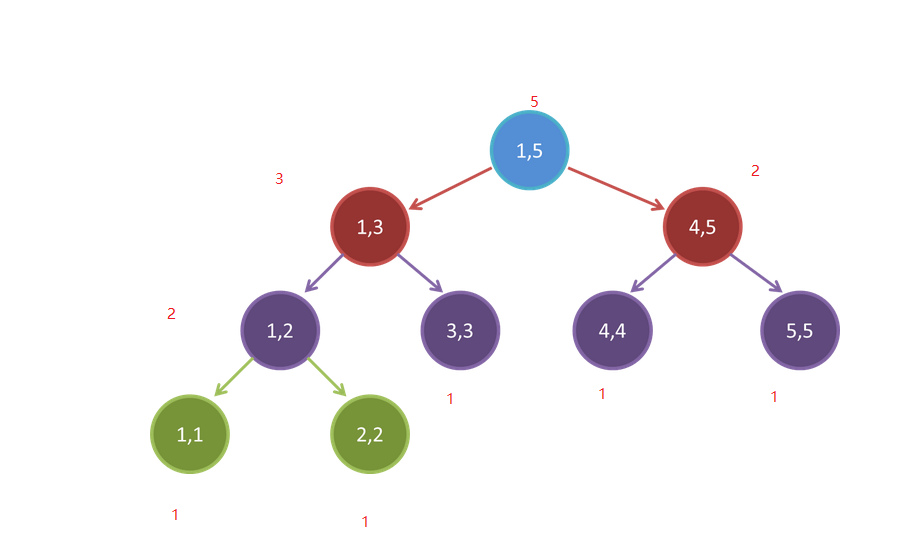
有了懒惰标记这种神奇的东西,我们区间修改时就可以偷一下懒,先修改当前节点,然后直接把信息挂在节点上就可以了!
如下面这棵线段树,当我们要修改区间【1,4】,将元素赋值为1时,我们可以先找到所有的整个区间都要被修改的节点,显然是储存区间【1,3】和【1,4】的这两个节点。我们就可以先把【1,3】的sum改为3((3−1+1)∗1=3,把【4,4】的sum改为1((1−1+1)∗1=1然后给它们打上值为1的懒惰标记,然后就可以了。这样一来,我们每一次修改区间时只要找到目标区间就可以了,不用再向下递归到叶节点。
示例代码:
void changeSegment(int p,int l,int r,int x)
//当前到了编号为p的节点,要把[l..r]区间中的所有元素的值+x
{
if(tr[p].l==l&&ytr[p].r==r)//如果找到了全部元素都要被修改的区间
{
tr[p].sum+=(r-l+1)*x;
//更新该区间的sum
tr[p].lazy+=x;
return;
//懒惰标记叠加
}
int mid=(tr[p].l+tr[p].r)>>2;
if(r<=mid) changeSegment(p*2,l,r,x);
//如果被修改区间完全在左区间
else if(l>mid) changeSegment(p*2+1,l,r,x);
//如果被修改区间完全在右区间
else changeSegment(p*2,l,mid,x),changeSegment(p*2+1,mid+1,r,x);
//如果都不在,就要把修改区间分解成两块,分别往左右区间递归
update(p);
//记得更新点k的值
}
请注意:某些题目的懒惰标记属于绝对标记(如维护区间平方和),一定要先下传标记,再向下递归。
pusudown
碰到相对标记这种容易欺负的小朋友,我们只用打一下懒惰标记就可以了。
但是,遇到绝对标记,或是下文提到的区间查询,简单地打上懒惰标记就明显GG了。毕竟,懒惰标记只是简单地在节点挂上一个信息而已,遇到复杂的情况可是不行的啊!
于是,懒惰标记的下传操作就诞生了。
顾名思义,下传标记就是把一个节点的懒惰标记传给它的左右儿子,再把该节点的懒惰标记删去。
我们先来回顾一下标记的含义:
- 标记的含义:本区间已经被更新过了,但是子区间却没有被更新过,被更新的信息是什么
显然,父区间是包含子区间的,也就是对于父区间的标记和子区间是有联系的。在大多数情况下,父区间和子区间的标记是相同的。因此,我们可以由父区间的标记推算出子区间应当是什么标记。
注意:以下所说的问题都是指区间赋值,除非有什么特别的申明。
如果要给一个节点中的所有元素重新赋值为x,那么它的儿子也必定要被赋值成x。所以,我们直接在子节点处修改sum值,再把子节点的标记改变一下就可以了(由于区间赋值要用绝对标记,因此当子节点已经有标记时,要先下传子节点的标记,再下传该节点的标记。但是区间赋值会覆盖掉子节点的值,因此在这个问题中,直接修改标记就可以了)
区间+x代码如下:
void pushdown(int p)//将点p的懒惰标记下传
{
if(tr[p].l==tr[p].r){tr[p].lazy=0;return;}
//如果节点k已经是叶节点了,没有子节点,那么标记就不用下传,直接删除就可以了
tr[p*2].sum+=(tr[p*2].r-tr[p*2].l+1)*tr[p].lazy;
tr[p*2+1].sum+=(tr[p*2+1].r-tr[p*2+1].l+1)*tr[k].lazy;
//给p的子节点重新赋值
tr[p*2].lazy+=tr[p].lazy;
tr[p*2+1].lazy+=tr[p].lazy;
//下传点k的标记
tr[p].lazy=0;//记得清空点k的标记
}
那么区间赋值就很容易解决了。我们直接修改当前节点的sum,再打上标记就可以了。在大多数问题中,我们要先下传当前节点的标记,再打上标记。但由于这个问题的特殊性,我们就不用先下传标记了。
区间查询
上面我们很轻松地解决了修改的问题,于是我们就维护了一个完整的在线线段树了。但是光有维护是没用的,我们还要处理询问的问题。最常见的莫过于区间查询了,如询问区间[l…r]中所有数的和。
这其实和区间修改是类似的。我们也分类讨论:
- 当查找区间在当前区间的左子区间时,递归到左子区间;
- 当查找区间在当前区间的右子区间时,递归到右子区间;
- 否则,这个区间一定是跨越两个子区间的,我们就把它切成2块,分在两个子区间查询。
最后把答案合起来处理就可以了(如查询区间和时就把两块区间的和加起来,查询最大值时就返回两块区间的最大值)
最后强调一个细节:记得在查询之前下传标记!!!
下面贴上查询区间和的代码:
int ask(int k,int l,int r)
//当前到了编号为k的节点,查询[l..r]的和
{
if(tr[k].lazy) pushdown(k);
//如果当前节点被打上了懒惰标记,那么就把这个标记下传,这一句其实也可以放在下一语句的后面
if(tr[k].l==l&&tr[k].r==r) return tr[k].sum;
//如果当前区间就是询问区间,完全重合,那么显然可以直接返回
int mid=(tr[k].l+tr[k].r)>>2;
if(r<=mid) return ask(k*2,l,r);
//如果询问区间包含在左子区间中
if(l>mid) return ask(k*2+1,l,r);
//如果询问区间包含在右子区间中
return ask(k*2,l,mid)+ask(k*2+1,mid+1,r);
//如果询问区间跨越两个子区间
}
访问最大值
int ask(int k,int l,int r){
//访问【l,r】最大值
if(l<=tr[k].l&&r==t[k].r) return t[k].dat;
//完全包含
int mid=(tr[k].l+tr[k].r)>>1;
//折半
int val=-1>>30;
//负无穷
if(l<=mid)val=max(val,ask(k*2,l,r));
//左子节点有重叠
if(r>mid)val=max(val,ask(l*2+1,l,r));
//右子节点有重叠
return val;
}
题目
单点更新
1.hdu1166 敌兵布阵 :有N个兵营,每个兵营都给出了人数ai(下标从1开始),有四种命令,(1)”Addij”,表示第i个营地增加j人。(2)“Sub i j”,表示第i个营地减少j人。(3)“Query ij”,查询第i个营地到第j个营地的总人数。(4)”End“,表示命令结束。
解题代码:
#include<iostream>
#include<cstdio>
#include<cstring>
#define maxn 1<<17
using namespace std;
int size,n,sum,all[40010];
struct line
{
int l,r;
int n;
}a[maxn];
void init()
{
int i;
for(n=1;n<size;n<<=1);
for(i=n;i<2*n;i++)
{
a[i].l=a[i].r=i-n+1;
a[i].n=0;
}
for(i=n-1;i>0;i--)
{
a[i].l=a[2*i].l;
a[i].r=a[2*i+1].r;
a[i].n=0;
}
}
void insert(int i,int x,int m)
{
if(x>=a[i].l && x<=a[i].r) a[i].n+=m;
if(a[i].l==a[i].r) return;
int mid=(a[i].l+a[i].r)/2;
if(x>mid) insert(2*i+1,x,m);
else insert(2*i,x,m);
}
void find(int x,int y,int i)
{
if(x==a[i].l && y==a[i].r)
{
sum+=a[i].n;
return;
}
if(a[i].l==a[i].r) return;
int mid=(a[i].l+a[i].r)/2;
if(x>mid) find(x,y,2*i+1);
else if(y<=mid) find(x,y,2*i);
else
{
find(x,mid,2*i);
find(mid+1,y,2*i+1);
}
}
int main()
{
int i,j,k,t,x,y,m;
char s[7];
scanf("%d",&t);
for(i=0;i<t;i++)
{
scanf("%d",&size);
init();
for(j=0;j<size;j++)
{
scanf("%d",&k);
insert(1,j+1,k);
}
k=0;
while(scanf("%s",s)!=EOF && strcmp(s,"End"))
{
if(strcmp(s,"Add")==0)
{
scanf("%d%d",&x,&m);
insert(1,x,m);
}
else if(strcmp(s,"Sub")==0)
{
scanf("%d%d",&x,&m);
insert(1,x,-m);
}
else
{
scanf("%d%d",&x,&y);
sum=0;
find(x,y,1);
all[k++]=sum;
}
}
printf("Case %d:\n",i+1);
for(j=0;j<k;j++) printf("%d\n",all[j]);
}
return 0;
}
后序请自己自行百度
2.hdu1754 I Hate It :给你N个数,M个操作,操作分两类。(1)”QAB“,查询区间[A,B]内的最大值。(2)”UAB”,将第A个数的值改成B。
3.hdu1394Minimum Inversion Number :给你N个数,要求统计它的所有形式的逆序对的最小值。它的所有形式的意思是,不断将数组开头的第一个数放到数组的最后面。
4.hdu2795 Billboard :有一块板,规格为hw,然后有n张海报,每张海报的规格为1wi,选择贴海报的位置是:尽量高,同一高度,选择尽量靠左的地方。要求输出每张海报的高度位置。
5.poj2828 BuyTickets :有N个人排队,每一个人都有一个val来对应,每一个后来人都会插入当前队伍的某一个位置pos。要求把队伍最后的状态输出。
区间更新
简单的说明:成段更新需要用到延迟标记(或者说懒惰标记),简单来说就是每次更新的时候不要更新到底,用延迟标记使得更新延迟到下次需要更新or询问到的时候。延迟标记的意思是:这个区间的左右儿子都需要被更新,但是当前区间已经更新了。
1.hdu1698 Just a Hook :给你T组数据,N个数(初始时每个数的值为1),M个操作,每个操作把区间[a,b]里的数更新为c,问最后这N个数的和是多少。
题解:
#include <cstdio>
#include <cstring>
using namespace std;
#define LL(x) (x<<1)
#define RR(x) (x<<1|1)
#define MID(a,b) (a+((b-a)>>1))
const int N=100005;
struct node
{
int lft,rht;
int valu,type;
int mid(){return MID(lft,rht);}
void fun(int tmp)
{
type=tmp;
valu=(rht-lft+1)*type;
}
};
struct Segtree
{
node tree[N*4];
void build(int lft,int rht,int ind)
{
tree[ind].lft=lft; tree[ind].rht=rht;
tree[ind].valu=rht-lft+1;
tree[ind].type=1;
if(lft!=rht)
{
int mid=tree[ind].mid();
build(lft,mid,LL(ind));
build(mid+1,rht,RR(ind));
}
}
void updata(int st,int ed,int ind,int type)
{
int lft=tree[ind].lft,rht=tree[ind].rht;
if(st<=lft&&rht<=ed) tree[ind].fun(type);
else
{
if(tree[ind].type)
{
tree[LL(ind)].fun(tree[ind].type);
tree[RR(ind)].fun(tree[ind].type);
tree[ind].type=0;
}
int mid=tree[ind].mid();
if(st<=mid) updata(st,ed,LL(ind),type);
if(ed>mid) updata(st,ed,RR(ind),type);
tree[ind].valu=tree[LL(ind)].valu+tree[RR(ind)].valu;
}
}
}seg;
int main()
{
int t,t_cnt=0;
scanf("%d",&t);
while(t--)
{
int n,m,a,b,c;
scanf("%d%d",&n,&m);
seg.build(1,n,1);
while(m--)
{
scanf("%d%d%d",&a,&b,&c);
seg.updata(a,b,1,c);
}
printf("Case %d: The total value of the hook is %d.\n",++t_cnt,seg.tree[1].valu);
}
return 0;
}
2.poj3468 A SimpleProblem with Integers :给你N个数,然后有M个操作。有两种类型的操作,(1)“Ca b c”,表示将区间[a,b]里的数加上c。(2)“Q a b”,表示查询区间[a,b]的数的和.
3.poj2528 Mayor’sposters :有t组测试数据,有n张海报,海报按题目给出的顺序覆盖,问最后能看到几张海报。
4.poj2991 Crane :有N根杆子,前后两根杆子通过一个节点连接,每个节点可以旋转一定的角度,每次给你一个操作(s,a)表示将第s与s+1之间的角度修改为a度,并且每次操作之后都需要求出第N个节点的位置。
区间合并
1.poj3667 Hotel :有N个房间,M次操作。有两种操作(1)”1a”,表示找到连续的长度为a的空房间,如果有多解,优先左边的,即表示入住。(2)”2 b len”,把起点为b长度的len的房间清空,即退房。
2.hdu3308 LCIS :给你N个整数,有两种操作,(1)”U A B”,表示把第A个数变成B,”QAB”,表示查询区间[A,B]的最长连续上升序列。
3.hdu3397 Sequence operation :有N个为0或为1的数,有M个操作,操作有5种类型。(1)“0 a b”,表示将区间[a,b]范围内的数全部置0。(2)“1 a b”,表示将区间[a,b]内的数全部置1。(3)”2 a b”,表示将区间[a,b]内的数0变成1,1变成0。(4)”3ab”,表示查询[a,b]范围内1的数。(5)”4 a b”,表示查询[a,b]范围内最长的连续的1。
4.hdu2871 Memory Control :给N个单位内存(编号从1开始),有4种操作,(1)”Reset”,表示把所有的内存清空,然后输出”Reset Now”。(2)”New x”,表示申请一块长度为x的内存块(如多解,左边优先),然后输出”New at A”,A表示该内存块的起点。(3)”Free x”,表示把包含第x块单位内存的内存块清除,然后输出”Free from A toB”,A和B分别表示该内存块的起点和终点(4)”Get x”,表示返回第x块内存块的起始内存单位编号,然后输出 “Get at A”。
5.hdu1540 Tunnel Warfare :有N个村子排成一条直线,每个村子都连接了它的左右两个村子(除了最左边和最右边的外),有3种操作,(1)”D x”,表示将第x个村子摧毁。(2)”Qx”,表示查询与第x个村子直接和间接相连的村子有多少个。(3)”R”,表示将最早摧毁的村子复原。。
6.CodeforcesBeta Round #43 D. Parking Lot :有一条长度为L的街道,有N个操作,操作有两种,(1)”1 a”,表示有一辆长度为a的车开进来想找停车位,停车位必须满足与它前面的车距离至少为b,与后面的车距离至少为f.如果能找到这样的停车位,输出这辆车的起始位置(且这个位置最小),否则输出-1。(2)”2 a”,表示第a个事件里进来停车的那辆车开出去了。
#include <iostream>
#include <cstdio>
#include <cstring>
#include <vector>
using namespace std;
#define LL(x) (x<<1)
#define RR(x) (x<<1|1)
#define MID(a,b) (a+((b-a)>>1))
const int N=100005;
struct node
{
int lft,rht;
int lmx,rmx,mx,flag;
int len(){return rht-lft;}
int mid(){return MID(lft,rht);}
void init(){lmx=rmx=mx=len();}
void fun(int valu)
{
if(valu==1) lmx=rmx=mx=0;
else lmx=rmx=mx=len();
flag=valu;
}
};
int n,m,b,f;
int st[N],ed[N];
struct Segtree
{
node tree[N*4];
void down(int ind)
{
if(tree[ind].flag)
{
tree[LL(ind)].fun(tree[ind].flag);
tree[RR(ind)].fun(tree[ind].flag);
tree[ind].flag=0;
}
}
void up(int ind)
{
tree[ind].lmx=tree[LL(ind)].lmx;
tree[ind].rmx=tree[RR(ind)].rmx;
tree[ind].mx=max(tree[LL(ind)].mx,tree[RR(ind)].mx);
if(tree[LL(ind)].lmx==tree[LL(ind)].len())
tree[ind].lmx+=tree[RR(ind)].lmx;
if(tree[RR(ind)].rmx==tree[RR(ind)].len())
tree[ind].rmx+=tree[LL(ind)].rmx;
tree[ind].mx=max(tree[ind].mx,tree[LL(ind)].rmx+tree[RR(ind)].lmx);
tree[ind].mx=max(tree[ind].mx,max(tree[ind].lmx,tree[ind].rmx));
}
void build(int lft,int rht,int ind)
{
tree[ind].lft=lft; tree[ind].rht=rht;
tree[ind].flag=0; tree[ind].init();
if(lft+1!=rht)
{
int mid=tree[ind].mid();
build(lft,mid,LL(ind));
build(mid,rht,RR(ind));
}
}
void updata(int st,int ed,int ind,int valu)
{
int lft=tree[ind].lft,rht=tree[ind].rht;
if(st<=lft&&rht<=ed) tree[ind].fun(valu);
else
{
down(ind);
int mid=tree[ind].mid();
if(st<mid) updata(st,ed,LL(ind),valu);
if(ed>mid) updata(st,ed,RR(ind),valu);
up(ind);
}
}
int query(int valu,int ind)
{
down(ind);
int pos;
if(tree[LL(ind)].mx>=valu) pos=query(valu,LL(ind));
else if(tree[LL(ind)].rmx+tree[RR(ind)].lmx>=valu)
pos=tree[LL(ind)].rht-tree[LL(ind)].rmx;
else pos=query(valu,RR(ind));
up(ind);
return pos;
}
}seg;
int main()
{
while(scanf("%d%d%d%d",&n,&b,&f,&m)!=EOF)
{
seg.build(-b,n+f,1);
for(int i=1;i<=m;i++)
{
int cmd,len,pos=-1;
scanf("%d%d",&cmd,&len);
if(cmd==1)
{
if(seg.tree[1].mx>=len+b+f)
{
pos=seg.query(len+b+f,1)+b;
st[i]=pos,ed[i]=pos+len;
seg.updata(st[i],ed[i],1,1);
}
printf("%d\n",pos);
}
else
{
seg.updata(st[len],ed[len],1,-1);
}
}
}
return 0;
}
扫描线
1.acwing 247 Atlantis :给你N个矩形,每个矩形给出左下角的坐标,右上角的坐标。最后以N=0为结束。要你求出矩形并后的面积。
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;
const int N = 100010;
int n;
struct Segment
{
double x, y1, y2;
int k;
bool operator< (const Segment &t)const
{
return x < t.x;
}
}seg[N * 2];
struct Node
{
int l, r;
int cnt;
double len;
}tr[N * 8];
vector<double> ys;
int find(double y)
{
return lower_bound(ys.begin(), ys.end(), y) - ys.begin();
}
void pushup(int u)
{
if (tr[u].cnt) tr[u].len = ys[tr[u].r + 1] - ys[tr[u].l];
else if (tr[u].l != tr[u].r)
{
tr[u].len = tr[u << 1].len + tr[u << 1 | 1].len;
}
else tr[u].len = 0;
}
void build(int u, int l, int r)
{
tr[u] = {l, r, 0, 0};
if (l != r)
{
int mid = l + r >> 1;
build(u << 1, l, mid), build(u << 1 | 1, mid + 1, r);
}
}
void modify(int u, int l, int r, int k)
{
if (tr[u].l >= l && tr[u].r <= r)
{
tr[u].cnt += k;
pushup(u);
}
else
{
int mid = tr[u].l + tr[u].r >> 1;
if (l <= mid) modify(u << 1, l, r, k);
if (r > mid) modify(u << 1 | 1, l, r, k);
pushup(u);
}
}
int main()
{
int T = 1;
while (scanf("%d", &n), n)
{
ys.clear();
for (int i = 0, j = 0; i < n; i ++ )
{
double x1, y1, x2, y2;
scanf("%lf%lf%lf%lf", &x1, &y1, &x2, &y2);
seg[j ++ ] = {x1, y1, y2, 1};
seg[j ++ ] = {x2, y1, y2, -1};
ys.push_back(y1), ys.push_back(y2);
}
sort(ys.begin(), ys.end());
ys.erase(unique(ys.begin(), ys.end()), ys.end());
build(1, 0, ys.size() - 2);
sort(seg, seg + n * 2);
double res = 0;
for (int i = 0; i < n * 2; i ++ )
{
if (i > 0) res += tr[1].len * (seg[i].x - seg[i - 1].x);
modify(1, find(seg[i].y1), find(seg[i].y2) - 1, seg[i].k);
}
printf("Test case #%d\n", T ++ );
printf("Total explored area: %.2lf\n\n", res);
}
return 0;
}
总结
首先感谢你能阅读完!!!
由于博主水平有限,有错误请及时告知博主,以免误人子弟!!
利用线段树(就那五个方法),我们可以高效地询问和修改一个数列中某个区间的信息,并且代码也不算特别复杂。
但是线段树也是有一定的局限性的,其中最明显的就是数列中数的个数必须固定,即不能添加或删除数列中的数。
数据结构没有难题,只有反复训练!!!(码字不易)
谢谢 QAQ


收藏大于点赞系列
代码有问题
已修正!
大佬你好。。线段树定义那个pushup()函数里面不应该是tr[k].dat= max(tr[k2].dat, tr[k2+1].dat);吗???
感谢,已修正!(QwQ
没有修正啊。。。
抱歉!由于有保存问题没有及时解决,现在已经修正!望查阅!
tql
up主太新蜜蜂了,OORRZz
hhhh
博主tql…入门小白orz