石子合并
状态:f[i,j] 合并第i~j堆石子
属性:min
划分:最后合并的石子的下标为分界点
每个状态只会依赖比它长度更短的其他状态,所以先枚举长度可以保证在计算每个状态之前,先计算出它所依赖的状态。
//状态:f[i,j] 合并第i~j堆石子
//属性:min
//划分:最后合并的石子的下标为分界点
//每个状态只会依赖比它长度更短的其他状态,所以先枚举长度可以保证在计算每个状态之前,先计算出它所依赖的状态
#include<iostream>
#include<cstring>
using namespace std;
const int N=310;
int f[N][N];
int s[N];
int path[N][N];
//打印路径
void print_path(int l,int r)
{
if(l >= r)
return ;
int k=path[l][r];
print_path(l,k);
print_path(k+1,r);
printf("合并 %d 到 %d 这一堆和 %d 到 %d 这一堆\n", l, k, k + 1, r);
}
int main()
{
int n;
cin>>n;
for(int i=1;i<=n;i++)
cin>>s[i];
for(int i=1;i<=n;i++)
s[i]+=s[i-1];
memset(f,0x3f,sizeof f);
for(int len=1;len<=n;len++)
for(int l=1;l+len-1<=n;l++)//枚举起点
{
int r=l+len-1;//右端点
if(len==1)
f[l][r]=0;//合并不需代价
else
{
for(int k=l;k<r;k++)//枚举分界点(注意:右边至少留一堆)
{
//f[l][r]=min(f[l][r],f[l][k]+f[k+1][r]+s[r]-s[l-1]);
if(f[l][r] > f[l][k] + f[k+1][r] + s[r] - s[l-1])
{
f[l][r]=f[l][k] + f[k+1][r] + s[r] - s[l-1];
path[l][r]=k;
}
}
}
}
//print_path(1,n);
cout<<f[1][n]<<endl;
return 0;
}
优化
四边形不等式。不会QAQ,先占个坑。
poj3280
题目大意:
给定一个长M,由N个小写字母构成的字符串,每插入或者删除一个字符都需要一定的花费,增删字符的花费不同,问怎样可以使这个字符串变成一个回文串,且花费最小。
思路1
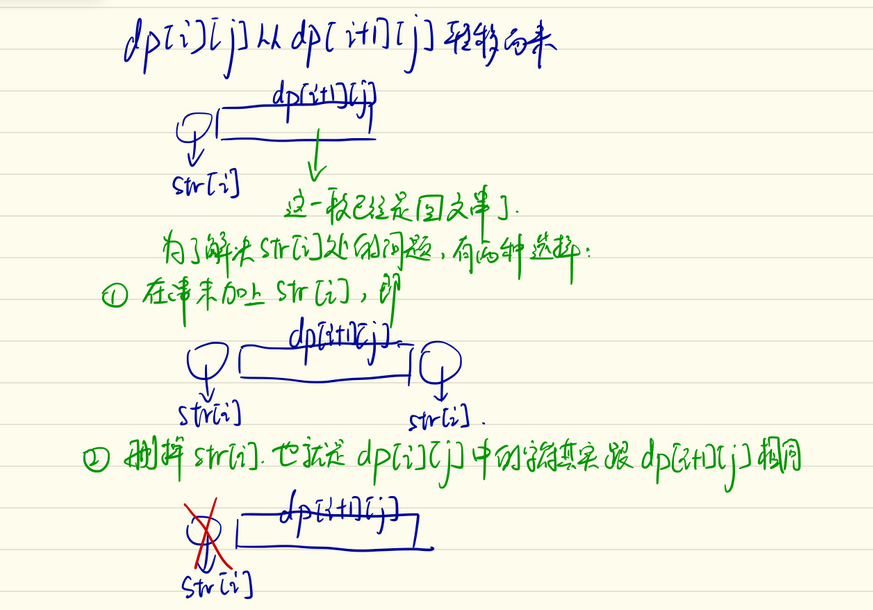
由于在一头加上一个字母和在另一头减去一个字母对于得到一个回文串来讲效果是等价的,但是这两种操作的花费可能不同。因此,需要添加或者删除字母的时候只需要选择这两种里面花费较小的那一种。
假设已经将区间[i,j]整理成为一个回文串,当DP到区间[i,j+1]时,我们可以在i-1的位置添加一个s[j+1]字符,或者将在j+1处的字符删除,得到一个新的回文串。因此从[i,j]到[i,j+1]的状态转移只相差一个增删s[j+1]字符的最小花费。


#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int N=2010;
char s[N];
int n,m;
int cost[30];
int dp[N][N];//dp[i][j] 存储从 i 到 j 这一段转换成回文子序列需要的最小花费
int main()
{
ios::sync_with_stdio(false);//将stdio解除绑定,使得cin与scanf效率相差无几
int a,b;
char t;
while(cin>>n>>m)
{
cin>>s+1;
while(n--)
{
cin>>t>>a>>b;
cost[t-'a']=min(a,b);
}
for(int i=m;i>=1;i--)
{
dp[i][i]=0;
for(int j=i+1;j<=m;j++)
{
if(s[i]==s[j]) dp[i][j]=dp[i+1][j-1];
else dp[i][j]=min(dp[i+1][j]+cost[s[i]-'a'],dp[i][j-1]+cost[s[j]-'a']);
}
}
printf("%d\n",dp[1][m]);
}
return 0;
}
i和j先循环哪个都行,只要保证i递减 && j递增 && i<=j
for(int j=1;j<=m;j++)
{
dp[j][j]=0;
for(int i=j-1;i>=1;i--)
{
if(s[i]==s[j]) dp[i][j]=dp[i+1][j-1];
else dp[i][j]=min((dp[i+1][j]+cost[s[i]-'a']),(dp[i][j-1]+cost[s[j]-'a']));
}
}
滚动数组优化
为了节省空间,可以只开两行的数组,因为每次更新只需要相邻行的数据。
#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int N=2010;
char s[N];
int n,m;
int cost[30];
int dp[2][N];//dp[i][j] 存储从 i 到 j 这一段转换成回文子序列需要的最小花费
int main()
{
ios::sync_with_stdio(false);//将stdio解除绑定,使得cin与scanf效率相差无几
int a,b;
char t;
while(cin>>n>>m)
{
cin>>s+1;
while(n--)
{
cin>>t>>a>>b;
cost[t-'a']=min(a,b);
}
for(int i=m;i>=1;i--)
{
dp[i&1][i]=0;
for(int j=i+1;j<=m;j++)
{
if(s[i]==s[j]) dp[i&1][j]=dp[i+1&1][j-1];
else dp[i&1][j]=min(dp[i+1&1][j]+cost[s[i]-'a'],dp[i&1][j-1]+cost[s[j]-'a']);
}
}
printf("%d\n",dp[1][m]);
}
return 0;
}
poj1159
题意:
给你一串字符串,让你求最少加入几个字符,才能使得这个字符串是个回文串。
思路1
设原序列S的逆序列为S’ ,这道题目的关键在于:
最少需要补充的字母数 = 原序列S的长度 — S和S’的最长公共子序列长度
原因:
(1)要求最少添加几个字符,我们可以先从原串中找到一个最长回文串,然后对于原串中不属于这个回文串的字符,在它关于回文串中心的对称位置添加一个相同字符即可。那么需要添加的字符数量即为n-最长回文串长度。
(2)最长回文串可以看作是原串中前面和后面字符的一种匹配(每个后面的字符在前面找到一个符合位置要求的与它相同的字符)。这种的回文匹配和原串与逆序串的公共子序列是一一对应的(一个回文匹配对应一个公共子序列,反之亦然),而且两者所涉及到的原串中的字符数量是相等的,也就是最长公共子序列对应最长回文串。
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<cmath>
using namespace std;
const int maxn = 5050;
char s1[maxn];
char s2[maxn];
int dp[2][maxn];
int n;
int LCS()//求最长公共子序列
{
for(int i=1;i<=n;i++)
{
for(int j=1;j<=n;j++)
{
if(s1[i] == s2[j])
dp[i&1][j]=dp[i-1&1][j-1]+1;
else
dp[i&1][j]=max(dp[i-1&1][j],dp[i&1][j-1]);
}
}
//cout<<dp[1][5]<<endl;
return dp[n&1][n];
}
int main()
{
scanf("%d", &n);
scanf("%s", s1+1);
for(int i=1;i<=n;i++)
s2[i]=s1[n-i+1];
printf("%d\n", n-LCS());
return 0;
}
思路2
用 f[i][j] 表示字符串 S[i..j] 中至少要插入的字符数量。
思考转移:
如果 S[i] == S[j],显然有 f[i][j] = f[i+1][j-1]
否则 f[i][j] = min(f[i][j-1], f[i+1][j]) + 1(左边加一个或者右边加一个,取min)
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<cmath>
using namespace std;
const int maxn = 5050;
char s1[maxn];
int dp[2][maxn];
int n;
int main()
{
scanf("%d", &n);
scanf("%s", s1+1);
for(int i=n;i>=1;i--)
{
for(int j=i+1;j<=n;j++)
{
if(s1[i]==s1[j]) dp[i&1][j]=dp[i+1&1][j-1];
else dp[i&1][j]=min(dp[i+1&1][j]+1,dp[i&1][j-1]+1);
}
}
printf("%d\n", dp[1][n]);
return 0;
}
uva10617
给定一个字符串,问有几种删字符的方案使得它变为回文串。
比如 ABA, 可以删掉 B、BA、AB、两个 A、不删。
字符串长度 ≤ 5000
用 f[i][j] 表示 S[i..j] 之间的回文串个数。
思考转移:
-
如果 S[i] == S[j],那么要统计 f[i+1][j], f[i][j-1],
这样会把 f[i+1][j-1] 统计两次,但是 f[i+1][j-1] 中的
回文串可以加上 S[i] 和 S[j] 再形成 f[i+1][j-1] 个回文串。
因此只要 f[i][j] = f[i+1][j] + f[i][j-1] + 1 即可。 -
如果 S[i] != S[j],那么要统计 f[i+1][j], f[i][j-1],
这样会把 f[i+1][j-1] 统计两次,此时 f[i+1][j-1] 中的
字符串不能通过新加一个字符得到新的回文串了,所以需要减掉多算的部分。
f[i][j] = f[i+1][j] + f[i][j-1] – f[i+1][j-1]
code
环形石子合并
Acwing1068
1、破环成链
2、求所有区间长度为n的链形石子合并
3.枚举长度为n的区间,取max
#include<iostream>
#include<cstring>
using namespace std;
const int N=410,INF=0x3f3f3f3f;
int f[N][N];
int g[N][N];
int s[N];
int w[N];
int main()
{
int n;
cin>>n;
for(int i=1;i<=n;i++)
{
cin>>w[i];
w[n+i]=w[i];
}
for(int i=1;i<=n*2;i++)
s[i]=s[i-1]+w[i];
memset(g,0x3f,sizeof g);
memset(f,-0x3f,sizeof f);
for(int len=1;len<=n;len++)
{
for(int l=1;l+len-1<=n*2;l++)
{
int r=l+len-1;
if(len == 1)
{
f[l][r]=0;
g[l][r]=0;
}
else
{
for(int k=l;k<r;k++)
{
f[l][r]=max(f[l][r],f[l][k]+f[k+1][r]+s[r]-s[l-1]);
g[l][r]=min(g[l][r],g[l][k]+g[k+1][r]+s[r]-s[l-1]);
}
}
}
}
int minv=INF,maxv=-INF;
for(int i=1;i<=n;i++)
{
minv=min(minv,g[i][n+i-1]);
maxv=max(maxv,f[i][n+i-1]);
}
cout<<minv<<endl;
cout<<maxv<<endl;
return 0;
}
#include<iostream>
#include<cstring>
#include<cstdio>
#include<algorithm>
using namespace std;
const int N=2010,INF=0x3f3f3f3f;
int f[N][N];
int sum[N];
int w[N];
int s[N][N];
int n;
int main()
{
while(~scanf("%d",&n))
{
for(int i=1;i<=n;i++)
{
scanf("%d",&w[i]);
w[n+i]=w[i];
}
for(int i=1;i<=n*2;i++)
{
sum[i]=sum[i-1]+w[i];
s[i][i]=i;
}
for(int len=2;len<=n;len++)
for(int l=1;l+len-1<=n*2;l++)
{
int r=l+len-1;
f[l][r]=INF;
for(int k=s[l][r-1];k<=s[l+1][r];k++)
{
if(f[l][k]+f[k+1][r]+sum[r]-sum[l-1] < f[l][r])
{
f[l][r]=f[l][k]+f[k+1][r]+sum[r]-sum[l-1];
s[l][r]=k;
}
}
}
int ans=INF;
for(int i=1;i<=n;i++)
ans=min(ans,f[i][i+n-1]);
printf("%d\n",ans);
}
return 0;
}
#include<iostream>
#include<cstring>
#include<cstdio>
#include<algorithm>
using namespace std;
const int N=110;
int f[N][N];
int w[N];
int n;
int main()
{
cin>>n;
for(int i=1;i<=n;i++)
scanf("%d",&w[i]);
n--;
for(int len=2;len<=n;len++)
for(int i=1;i+len-1<=n;i++)
{
int j=i+len-1;
f[i][j]=f[i+1][j]+w[i]*w[i+1]*w[j+1];
for(int k=i+1;k<j;k++)
f[i][j]=min(f[i][j],f[i][k]+f[k+1][j]+w[i]*w[k+1]*w[j+1]);
}
printf("%d\n",f[1][n]);
return 0;
}
能量项链
1、破环成链
2、求所有区间长度为n+1的项链合并成一个珠子
3.枚举长度为n+1的区间,取max
//f[l,r] :将[l,r]合并成一个珠子所释放的最大值
//划分:合并(l,k)所释放的最大值,合并(k,r)所释放的最大值,合并(l,k)和(k,r)所释放的最大值
#include<iostream>
#include<cstring>
using namespace std;
const int N=210,INF=0x3f3f3f3f;
int f[N][N];
int w[N];
int main()
{
int n;
cin>>n;
for(int i=1;i<=n;i++)
{
cin>>w[i];
w[n+i]=w[i];
}
memset(f,-0x3f,sizeof f);
for(int len=1;len <= n+1;len++)
{
for(int l=1;l+len-1<=n*2;l++)
{
int r=l+len-1;
if(len==1 || len ==2)
f[l][r]=0;
else
{
for(int k=l+1;k<r;k++)
f[l][r]=max(f[l][r],f[l][k]+f[k][r]+w[l]*w[r]*w[k]);
}
}
}
int res=0;
for(int i=1;i<=n;i++)
res=max(res,f[i][n+i]);
cout<<res<<endl;
return 0;
}
同样不会四边形优化QAQ
hdu4283
题目大意:
有 n 个人,每个人有一个diaosi[i]值,如果第 i 个人排在第k 位置,则他的愤怒值就为diaosi[i]*(k-1);等待过程中有一个黑屋子,可以把人暂时放到黑屋子里。使总的愤怒值最小;
思路
状态:dp[i][j]表示区间[i,j]的最小总不开心值
把区间[i,j]单独来看,则第i个人可以是第一个出场,也可以是最后一个出场(j-i+1),也可以是在中间出场(1 ~ j-i+1)。不妨设他是第k个出场的(1<=k<=j-i+1),那么根据栈后进先出的特点:
(1)第 i+1 到 i+k-1 总共有k-1个人要比i先出栈
(2)第 i+k 到j 总共j-i-k+1个人在i后面出栈
举个例子:有5个人事先排好顺序 1,2,3,4,5。入栈的时候,1入完2入,2入完3入,如果我要第1个人第3个出场,那么入栈出栈顺序是这样的:1入,2入,3入,3出,2出,1出(到此第一个人就是第3个出场啦,很明显第2,3号人要在1先出,而4,5要在1后出)
状态转移方程
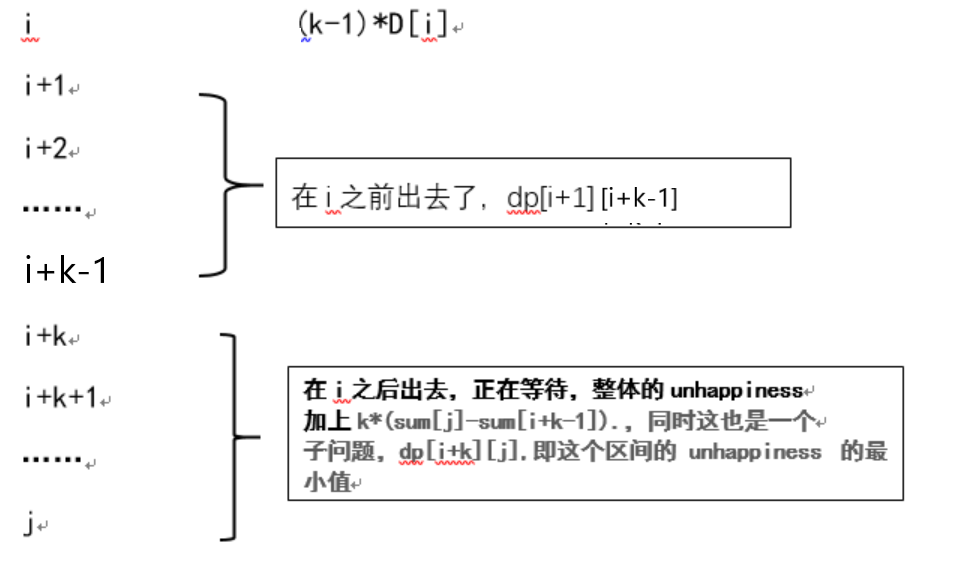
dp[i][j] = min(dp[i][j],dp[i+1][i+k-1]+dp[i+k][j] + (k-1)a[i] + (sum[j]-sum[i+k-1])k);
区间[i + k, j]在分析的时候是内部独立考虑的,所以在[i + k, j]上的最优解只是独立考虑[i + k, j]的最小值,在综合到[i, j]这个区间时由于[i, i + k - 1]这k个都在他们前面所以[i + k, j]这个最优解还要再加上D(i + k) * k + D(i + k + 1) * k + ...... + D(j) * k, (D(x)为第x个屌丝的屌丝值)。如果用前缀和来表示的话就是 (sum[j] - sum[i + k - 1]) * k
#include<iostream>
#include<cstring>
using namespace std;
const int N=110,INF=0x3f3f3f3f;
int n;
int d[N];
int s[N];
int f[N][N];//i到j的不开心值的最小值
int cnt;
int main()
{
int T;
cin>>T;
while(T--)
{
cin>>n;
for(int i=1;i<=n;i++)
{
cin>>d[i];
s[i]=s[i-1]+d[i];
}
for(int len=2;len<=n;len++)
{
for(int i=1;i+len-1<=n;i++)
{
int j=i+len-1;
f[i][j]=INF;
for(int k=1;k<=len;k++)
f[i][j]=min(f[i][j],f[i+1][i+k-1]+f[i+k][j]+(k-1)*d[i]+k*(s[j]-s[i+k-1]));
}
}
printf("Case #%d: %d\n",++cnt,f[1][n]);
}
}
第二种方法
两种方法区别主要是k,一个为i到j第几个出来,一个枚举k的下标(i~j)
for(int len=2;len<=n;len++)
{
for(int i=1;i+len-1<=n;i++)
{
int j=len+i-1;
f[i][j]=INF;
for(int k=i;k<=j;k++)
{
f[i][j]=min(f[i][j],f[i+1][k]+(k-i)*d[i]+(k-i+1)*(s[j]-s[k])+f[1+k][j]);
}
}
}
再搞一波记忆化搜索233333
#include<iostream>
#include<cstring>
#include<cstdio>
#include<algorithm>
using namespace std;
const int N=110,INF=0x3f3f3f3f;
int dp[N][N];
int a[N],sum[N];
int n;
int cnt;
int solve(int i,int j)
{
if(i>=j) return 0;
if(dp[i][j]!=-1) return dp[i][j];
dp[i][j]=INF;
for(int k=1;k<=j-i+1;k++)
{
dp[i][j]=min(dp[i][j],solve(i+1,i+k-1)+solve(i+k,j)+(k-1)*a[i]+(sum[j]-sum[i+k-1])*k);
}
return dp[i][j];
}
int main()
{
int t;
cin>>t;
while(t--)
{
cin>>n;
for(int i=1;i<=n;i++)
{
scanf("%d",&a[i]);
sum[i]=sum[i-1]+a[i];
}
memset(dp,-1,sizeof dp);
printf("Case #%d: %d\n",++cnt,solve(1,n));
}
return 0;
}
hdu4632
状态:dp[i][j] 表示字符串 s 的子串 s[i..j] 中包含的回文子序列的数量。
区间DP,dp[i][j]表示从第i个到第j个有多少个回文子序列,将所有dp[i][i]初始化为1(题目要求,一个字母也为回文),其他为0.
状态转移:因为是记录子序列的数目,i~j的子序列就前一个状态推导过来,而i~j的前一个状态有两个(i+1)~j和i
~(j-1),很明显要这两个相加,但是(i+1)~j和i~(j-1)相加有一段重复了,因为这两个都包含这(i+1)~(j-1),故而减去一个,所以可以得到第一个状态转移方程:dp[i][j]=dp[i+1][j]+dp[i][j-1]-dp[i+1][j-1]; 然后当字符串s[i]==s[j]时,即这两个字母相同,也就是可以组成回文,那么就是和(i+1)~(j-1)状态的回文组成新的回文序列,所以第二个状态转移方程就是:dp[i][j]=dp[i][j]+dp[i+1][j-1]+1.
另外呢,记得答案要取模,此处取模有个坑,就是第一个状态转移方程涉及减法,直接取模有可能为负数,必须要先加一下mod
(1)当i<j且s[i]!=s[j]时, dp[i][j] = dp[i][j-1] ∪ dp[i+1][j] (这里“∪”符号表示)两个集合的并,
根据容斥原理,我们可以得到:dp[i][j] = dp[i][j-1] ∪ dp[i+1][j] = dp[i][j-1] + dp[i+1][j] - dp[i+1][j-1]
(2)当i<j且s[i]==s[j]时,dp[i][j]的构成除了上述部分以外,还有 s[i] + s’ + s[j] 部分,其中 s’ 表示 s[i+1..j-1] 中的任意一个回文串,所以此时:dp[i][j] = dp[i][j-1] ∪ dp[i+1][j] + dp[i+1][j-1] + 1 = dp[i][j-1] + dp[i+1][j] + 1
#include<cstdio>
#include<iostream>
#include<cstring>
using namespace std;
const int maxn = 1010;
const int mod = 10007;
char a[maxn];
int n,dp[maxn][maxn];
int solve()
{
memset(dp,0,sizeof(dp));
for(int i = n ; i >= 1 ;i--)
{
dp[i][i]=1;
for(int j = i+1 ;j <= n ; j++)
{
if(a[i] == a[j])
dp[i][j] = (dp[i+1][j] + dp[i][j-1]+ 1) % mod;
else
dp[i][j] = ( dp[i+1][j] + dp[i][j-1]- dp[i+1][j-1] + mod) % mod;
}
}
return dp[1][n];
}
int main(){
int T;
cin>>T;
for(int cnt = 1 ; cnt <= T; cnt++)
{
scanf("%s",a+1);
n = strlen(a+1);
printf("Case %d: %d\n",cnt,solve());
}
return 0;
}
hdu2476
题意:
要把a串变成b串,每操作一次,可以使a串的[l,r]区间变为相同的一个字符。问把a变成b最少操作几次。
例如zzzzzfzzzzz,长度为11,下标看做0~10
先将0~10用画笔刷一次,变成aaaaaaaaaaa
1~9刷一次,abbbbbbbbba
2~8: abcccccccba
3~7: abcdddddcba
4~6: abcdeeedcab
5: abcdefedcab
这样就6次,变成了s2串了
思路
状态:dp[l][r]代表区间(l,r)里,最小次数把这个区间的A变成B。
当检查l位置A与B的时候,如果相同,dp[l][r] = dp[l+1][r];如果不同,dp[l][r] = dp[l+1][r]+1,
然后需要在区间(l+1,r)查找B[k]下是否有A[l]字符,dp[l][r] = dp[l+1][k]+dp[k+1][j]。
但是这样是不正确的,因为(l,k)的区间改变会改变A串。导致没办法区间合并。因为一旦需要考虑对某一段成段染色的话,在区间合并的时候,就无法考虑转移过程中起始串的变化了。既然这样,就不考虑成段染色造成的影响了,就当起始串和目标串处处不想等。
正解:
(1)dp[l][r] 表示把一个空字符串K的[l,r] 变成 对应B[l,r]这段的最小花费。
那么 dp[l][r] 就是 把 K[l] -> B[l], 然后再把K[l+1, r] -> B[l+1, r]
即: dp[l][r] = 1 + dp[l+1, r];
但是若存在B[l] = B[k] ( l+1 <=k <= r)
那就可以先把空串 K[l, k] -> B[l], 然后再对 K[l+1, k] 操作。
所以若 b[l] == b[k] 则 dp[l, r] = dp[l+1, k] + dp[k+1, r];
若 b[l]!=b[k] ,那K[l] 变成b[l] 还是需要一步操作, : dp[l, r] = dp[l+1, k] + dp[k+1, r] +1;
(2)sum[i] 表示把a[1,i] -> b[1,i]的最小花费,简单dp
对于当前考虑的第i个字符
1、如果a[i]==b[i],可以考虑不用刷i;
2、如果a[i]!=b[i],肯定有一段A的区间[k … i]被刷子刷过,在[1,i-1]中枚举刷的起点k,将[k,i]当做没有颜色来刷成B状态
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <iostream>
using namespace std;
const int INF = 0x3f3f3f3f;
const int N = 110;
char a[N],b[N];
int sum[N];
int dp[N][N];
int main()
{
while(~scanf("%s%s",a+1,b+1))
{
memset(dp,0,sizeof(dp));
int n = strlen(a+1);
for(int len = 1; len <= n; len++)
{
for(int l = 1; l+len-1 <= n; l++)
{
int r=l+len-1;
dp[l][r]=INF;
if(len == 1)
dp[l][r]=1;
for(int k = l+1; k <= r; k++)
{
if(b[k] == b[l])
dp[l][r] = min(dp[l][r],dp[l+1][k]+dp[k+1][r]);
else
dp[l][r]=min(dp[l][r],dp[l+1][k]+dp[k+1][r]+1);
}
}
}
for(int i = 1; i <= n; i++)
{
if(a[i] == b[i])
sum[i] = sum[i-1];
else
{
sum[i] = dp[1][i];
for(int j = 1; j <= i; j++)//枚举1_i中将哪个位置j粉刷使得j~i刷为a[i]
sum[i] = min(sum[i],sum[j-1]+dp[j][i]);
}
}
printf("%d\n",sum[n]);
}
return 0;
}
再贴一个hdoj看到的
const int N = 105;
int dp[N][N];
char a[N], b[N];
int main() {
while(~scanf("%s", a+1)) {
scanf("%s", b+1);
int n = strlen(b+1);
for (int i = n; i >= 1; --i) {
for (int j = i; j <= n; ++j) {
dp[i][j] = j-i+1;
for (int k = i+1; k <= j; ++k) {
if(b[i] == b[k]) dp[i][j] = min(dp[i][j], dp[i+1][k]+dp[k+1][j]);
else dp[i][j] = min(dp[i][j], dp[i][k]+dp[k+1][j]);
}
}
}
for (int i = n; i >= 1; --i) {
for (int j = i; j <= n; ++j) {
for (int k = i; k <= j; ++k) {
if(a[k] == b[k]) dp[i][j] = min(dp[i][j], dp[i][k-1]+dp[k+1][j]);
}
}
}
printf("%d\n", dp[1][n]);
}
return 0;
}
贴几个类似题
最短编辑距离
状态 f[i,j] :字符串A的前i个字母和字符串B的前j个字母匹配所需的最小操作步数
属性:min
状态划分:
(1)删。A[1~i-1]已经和B[1~j]匹配,此时删去A[i]即可
f[i][j]=min(f[i][j],f[i-1][j]+1);
(2)增。A[1~i]已经和B[1~j-1]匹配,此时在串A后增加B[j]即可
f[i][j]=min(f[i][j],f[i][j-1]+1);
(3)改。若A[i] == B[j] ,则f[i][j] = f[i-1][j-1]; 若A[i] != B[j] ,则f[i][j] = f[i-1][j-1]+1;
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1010;
int n, m;
char a[N], b[N];
int f[N][N];
int main()
{
scanf("%d%s", &n, a + 1);
scanf("%d%s", &m, b + 1);
for (int i = 0; i <= m; i ++ ) f[0][i] = i;//A为空,增加i个字母可和B相同
for (int i = 0; i <= n; i ++ ) f[i][0] = i;//A长度为i,删除i个字母后和B相同
for (int i = 1; i <= n; i ++ )
for (int j = 1; j <= m; j ++ )
{
f[i][j] = min(f[i - 1][j] + 1, f[i][j - 1] + 1);
if (a[i] == b[j]) f[i][j] = min(f[i][j], f[i - 1][j - 1]);
else f[i][j] = min(f[i][j], f[i - 1][j - 1] + 1);
}
printf("%d\n", f[n][m]);
return 0;
}
编辑距离
和上题一样,时间复杂度O(nm*nm),1e8,时限2s,可以水过
#include <iostream>
#include <algorithm>
#include <string.h>
using namespace std;
const int N = 15, M = 1010;
int n, m;
int f[N][N];
char str[M][N];
int edit_distance(char a[], char b[])
{
int la = strlen(a + 1), lb = strlen(b + 1);
for (int i = 0; i <= lb; i ++ ) f[0][i] = i;
for (int i = 0; i <= la; i ++ ) f[i][0] = i;
for (int i = 1; i <= la; i ++ )
for (int j = 1; j <= lb; j ++ )
{
f[i][j] = min(f[i - 1][j] + 1, f[i][j - 1] + 1);
f[i][j] = min(f[i][j], f[i - 1][j - 1] + (a[i] != b[j]));
}
return f[la][lb];
}
int main()
{
scanf("%d%d", &n, &m);
for (int i = 0; i < n; i ++ ) scanf("%s", str[i] + 1);
while (m -- )
{
char s[N];
int limit;
scanf("%s%d", s + 1, &limit);
int res = 0;
for (int i = 0; i < n; i ++ )
if (edit_distance(str[i], s) <= limit)
res ++ ;
printf("%d\n", res);
}
return 0;
}
poj2955
为了方便起见,我们这里将“最长规则的括号序列”简称为“目标序列”。
我们用 dp[L][R] 表示 字符串 s 的子串 s[L..R]
- 如果字符串 s是空串,或者它的长度为1,那么它的目标序列的长度肯定是 0 ;
- 如果字符串 s 的长度为2, 那么当 s==”()” 或者 s==”[]”的时候,它的目标序列的长度就是它本身的长度2;否则,它的目标序列的长度为0。
- 当 s[L]==’(‘ 并且 s[R]==’)’ 或者 s[L]==’[‘ 并且 s[R]==’]’ 的时候, dp[L][R] 的一种备选方案(称为第1中备选方案)是 dp[L+1][R-1] + 2;
- 不过 (s’) 或者 [s’] (这里 s’ 用于表示 s[L+1 .. R-1] 的目标序列)条件不一定是成立的,所以任何条件下都成立的一种备选方案(称为第2种备选方案)是 max(dp[L+1][R], dp[L][R-1]),即我们剔除掉最左边的字符串,或者最右边的字符串所能够带来的效果;
- 还有一种情况是字符串 s[L..R] 是两个字符串拼接而成的,那么这种情况下,它的一种备选方案(称为第3种备选方案)是 max(dp[L][i] + dp[i+1][R]) ,其中 L+1≤i<R-1。
然后我们发现还可以合并第2种备选方案到第3中备选方案中,因为 max(dp[L+1][R], dp[L][R-1]) 其实就等于 max(dp[L][i] + dp[i+1][R]) ,其中 i=L或R-1。
所以第2及第3中备选方案合并到一起就是 max(dp[L][i] + dp[i+1][R]) ,其中 L≤i<R。


code
给你一个字符串,里面只包含”(“,”)”,”[“,”]”四种符号,请问你需要至少添加多少个括号才能使这些括号匹配起来。
如:
[]是匹配的
([])[]是匹配的
((]是不匹配的
([)]是不匹配的
【题意】上一题求的是满足完美匹配的最大括号数量,而这题问的是使所有括号完美匹配需要添加的最小括号数量
显然,要使添加的括号尽量少,我们需要使原来的括号序列尽可能多得匹配,即先求最大匹配数量(跟上题一样),那么还剩下一些没有匹配的括号,我们就需要依次加上一个括号使它们得到匹配。综上所述,所求=原序列括号数量-最大匹配括号数量。(因此此题的代码与上题几乎一致)。
poj1141


当i>j时,直接返回,不需要输出
当i==j时,d[i][j]为1,至少要加一个括号,如果s[i]为’(‘ 或者’)’,输出”()”,否则输出”[]”
当i>j时,如果c[i][j] != -1,说明从i到j断开了,则递归调用print(i, c[i][j]);和print(c[i][j]+1, j);
如果c[i][j] == -1,说明没有断开,如果s[i]==’(‘ 则输出’(‘、 print(i+1, j-1); 和”)” ,否则输出”[” print(i+1, j-1);和”]”
code
poj1179
多角形是一个单人玩的游戏,开始时有一个N个顶点的多边形。如图,这里N=4。每个顶点有一个整数标记,每条边上有一个“+”号或“*”号。边从1编号到N。
- 第一步,一条边被拿走;随后各步包括如下:
- 选择一条边E和连接着E的两个顶点V1和 V2;
- 得到一个新的顶点,标记为V1与V2通过边E上的运算符运算的结果。
- 最后,游戏中没有边,游戏的得分为仅剩余的一个顶点的值。
用f(i,j)表示从点i到点j进行删边操作所能得到的最大值,num(i)表示第i个顶点上的数,若为加法,那么:
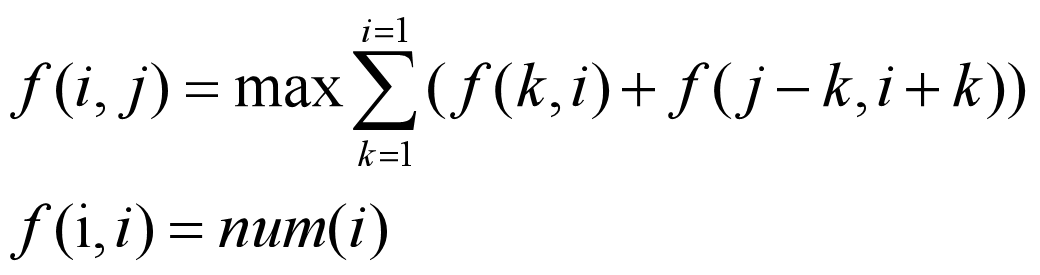
最后,我们允许顶点上出现负数。以前的方程还适不适用呢?
我们发现,两个负数的积为正数;这两个负数越小,它们的积越大。我们从前的方程,只是尽量使得局部解最大,而从来没有想过负数的积为正数这个问题。
对于加法,两个最优相加肯定最优,而对于乘法
求最大值:
- 正数×正数,如果两个都是最大值,则结果最大
- 正数×负数,正数最小,负数最大,则结果最大
- 负数×负数,如果两个都是最小值,则结果最大
求最小值:
- 正数×正数,如果两个都是最小值,则结果最小
- 正数×负数,正数最大,负数最小,则结果最小
- 负数×负数,如果两个都是最大值,则结果最小
我们引入函数fmin和fmax来解决这个问题。fmax(i,j)表示从点i开始,到但j为止进行删边操作所能得到的最大值,fmin(i,j) 表示最小值。
#include<iostream>
#include<cstring>
#include<algorithm>
#include<cstdio>
using namespace std;
const int N=110;
int Fmax[N][N],Fmin[N][N];
char op[N];
int a[N];
int n;
int main()
{
memset(Fmax,-0x3f,sizeof Fmax);
memset(Fmin,0x3f,sizeof Fmin);
cin>>n;
for(int i=1;i<=n;i++)
{
cin>>op[i]>>a[i];
op[i+n]=op[i];
a[i+n]=a[i];
}
for(int i=1;i<=n*2;i++) Fmax[i][i]=Fmin[i][i]=a[i];
for(int len=2;len<=n;len++)
for(int i=1;i+len-1<=n*2;i++)
{
int j=i+len-1;
for(int k=i;k<j;k++)
{
if(op[k+1] == 't')
{
Fmax[i][j]=max(Fmax[i][j],Fmax[i][k]+Fmax[k+1][j]);
Fmin[i][j]=min(Fmin[i][j],Fmin[i][k]+Fmin[k+1][j]);
}
else
{
Fmax[i][j]=max(Fmax[i][j],Fmax[i][k]*Fmax[k+1][j]);//同正
Fmax[i][j]=max(Fmax[i][j],Fmin[i][k]*Fmax[k+1][j]);//正*负
Fmax[i][j]=max(Fmax[i][j],Fmax[i][k]*Fmin[k+1][j]);//负*正
Fmax[i][j]=max(Fmax[i][j],Fmin[i][k]*Fmin[k+1][j]);//负*负
Fmin[i][j]=min(Fmin[i][j],Fmin[i][k]*Fmin[k+1][j]);//同正
Fmin[i][j]=min(Fmin[i][j],Fmax[i][k]*Fmin[k+1][j]);//正*负
Fmin[i][j]=min(Fmin[i][j],Fmin[i][k]*Fmax[k+1][j]);//负*正
Fmin[i][j]=min(Fmin[i][j],Fmax[i][k]*Fmax[k+1][j]);//负*负
}
}
}
int ans=-0x3f3f3f3f;
for(int i=1;i<=n;i++)
ans=max(ans,Fmax[i][i+n-1]);
printf("%d\n",ans);
for(int i=1;i<=n;i++)
if(Fmax[i][i+n-1] == ans)
printf("%d ",i);
return 0;
}
[hdu]
有一个n*m大小的蛋糕,上面有k个樱桃,现在我们需要把这个蛋糕切成k份,使每份蛋糕上有一个樱桃,问最小切割长度和。
用dp[i][j][k][l]表示以(i,j)为左上角,(k,l)为右下角的矩形切成每份一个樱桃的最小切割长度。然后就利用区间DP的作用,枚举切割点,从小区间转移到大区间。
边界条件:
假如里面没有樱桃,返回inf,因为不符合题意
假如里面有且仅有1颗樱桃,返回0
#include<iostream>
#include<cstring>
#include<algorithm>
#include<cstdio>
using namespace std;
const int N=25,INF=0x3f3f3f3f;
int f[N][N][N][N];
bool st[N][N];
int s[N][N];
int n,m,k;
int get(int x1,int y1,int x2,int y2)
{
return s[x2][y2]-s[x2][y1-1]-s[x1-1][y2]+s[x1-1][y1-1];
}
int dp(int a,int b,int c,int d)
{
if(~f[a][b][c][d]) return f[a][b][c][d];
int cnt=get(a,b,c,d);
if(cnt == 0) return f[a][b][c][d]=INF;//为0的话不能切,就是无穷大
if(cnt == 1) return f[a][b][c][d]=0;//1个就不用切割了
int ans=INF;
for(int i=a;i<c;i++) //横切
ans=min(ans,dp(a,b,i,d)+dp(i+1,b,c,d)+d-b+1);
for(int i=b;i<d;i++) //竖切
ans=min(ans,dp(a,b,c,i)+dp(a,i+1,c,d)+c-a+1);
return f[a][b][c][d]=ans;
}
int main()
{
int kas=1;
while(~scanf("%d%d%d",&n,&m,&k))
{
memset(f,-1,sizeof f);
memset(st,0,sizeof st);
for(int i=0;i<k;i++)
{
int x,y;
scanf("%d%d",&x,&y);
st[x][y]=1;
}
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
s[i][j]=s[i-1][j]+s[i][j-1]-s[i-1][j-1]+st[i][j];
printf("Case %d: %d\n",kas++,dp(1,1,n,m));
}
return 0;
}
hdu5115
题目大意是:有n头狼,初始攻击力为ai,然后可以只要活着就可以给左右两边的队友加buff,加bi点攻击力,也就是说你杀死一头狼一共会受到a[i]+b[i−1]+b[i+1]点伤害,现在要最小化杀死所有狼收到的伤害
设f[l][r]表示杀死l到r头狼受到的最小伤害,那么很容易得到转移方程
f[l][r]=min(f[l][r],f[l][k−1]+f[k+1][r]+a[k]+b[l−1]+b[r+1])
(设k为我们在杀死l到r头狼时最后杀死的那头狼)
#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
const int N=210,INF=0x3f3f3f3f;
int f[N][N];
int a[N],b[N];
int n;
int main()
{
int T;
cin>>T;
int kase = 1;
while(T--)
{
scanf("%d",&n);
for(int i=1;i<=n;i++) scanf("%d",&a[i]);
for(int i=1;i<=n;i++) scanf("%d",&b[i]);
a[n+1]=b[n+1]=0;
for(int i=1;i<=n;i++)
for(int j=i;j<=n;j++)
f[i][j]=INF;
for(int i=1;i<=n;i++)
f[i][i]=a[i]+b[i-1]+b[i+1];
for(int len=2;len<=n;len++)
for(int i=1;i+len-1<=n;i++)
{
int j=i+len-1;
for(int k=i;k<=j;k++)
f[i][j]=min(f[i][j],f[i][k-1]+f[k+1][j]+a[k]+b[i-1]+b[j+1]);
}
printf("Case #%d: %d\n",kase++,f[1][n]);
}
}
#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
const int N=55;
char s[N];
int f[N][N];
int main()
{
cin>>s+1;
int n=strlen(s+1);
for(int len=1;len<=n;len++)
for(int i=1;i+len-1<=n;i++)
{
int j=i+len-1;
f[i][j]=1e9;
if(len == 1) f[i][j]=1;
else if(s[i] == s[j]) f[i][j]=min(f[i+1][j],f[i][j-1]);
else
for(int k=i;k<=j;k++)
f[i][j]=min(f[i][j],f[i][k]+f[k+1][j]);
}
cout<<f[1][n]<<endl;
return 0;
}



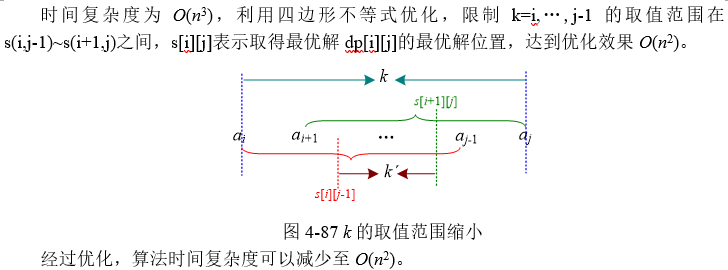


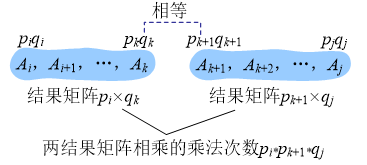

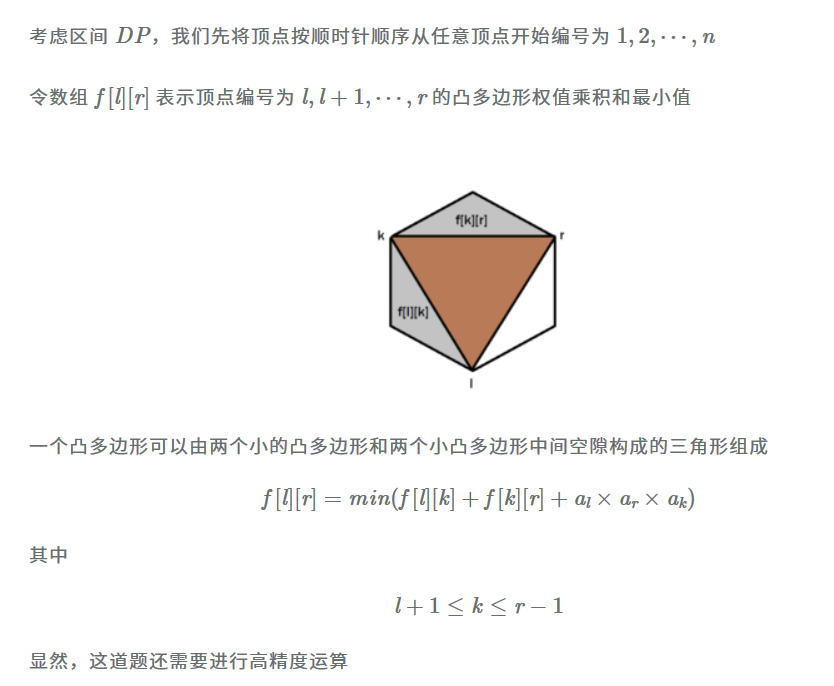




为什么那个poj3280那里要i递减j递增,直接使用模板遍历长度和起点也行吧
太强了,学习学习!
前排资瓷!!!