DP的笔记3(2坑)

作者： 作者的头像   豆浆灬油条 ,  2020-02-11 00:38:40 ,  所有人可见 ,  阅读 1100

6


8

1）状态机模型

首先感谢秦大佬的分享和y总的视频课,emmm…下面纯属个人理解(我这个蒟蒻真的理解了好久，有点难顶)

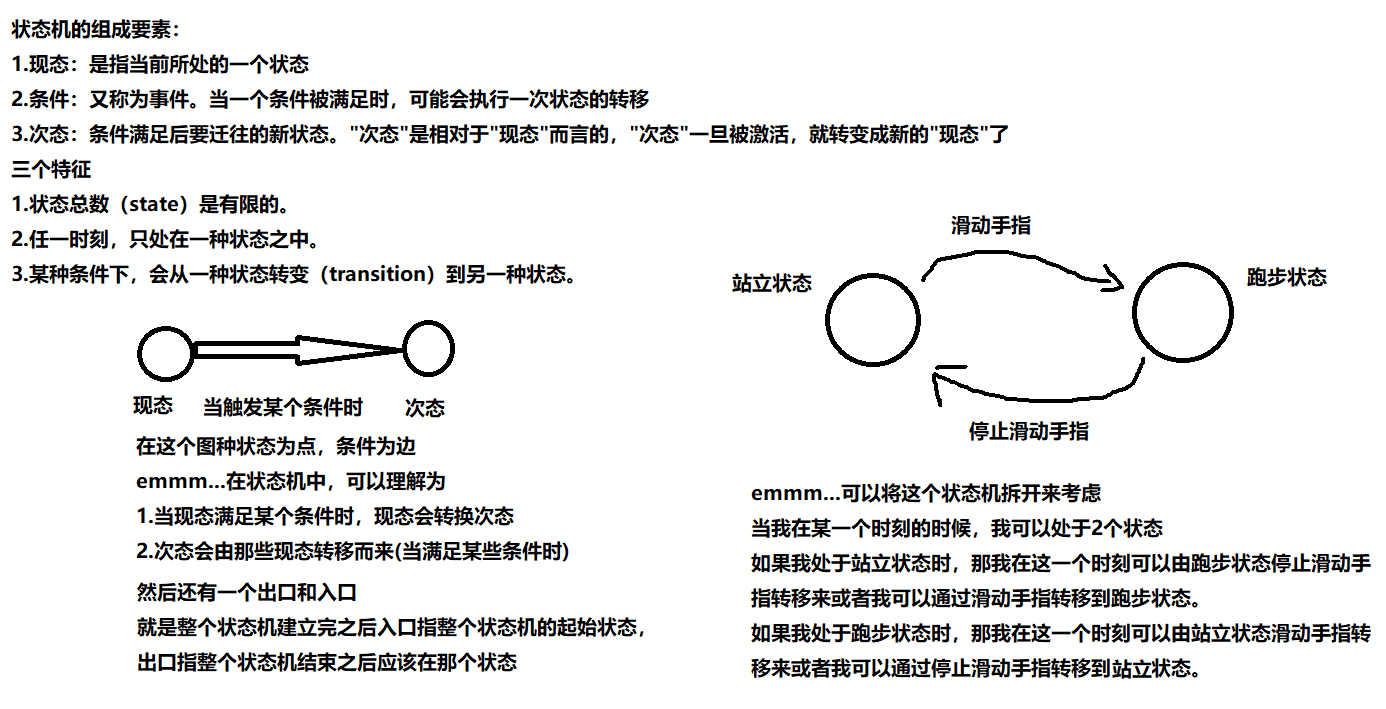
1.状态机的概念：表示有限个状态以及在这些状态之间的转移和动作等行为的数学模型。

1.png

大盗阿福

2.png 

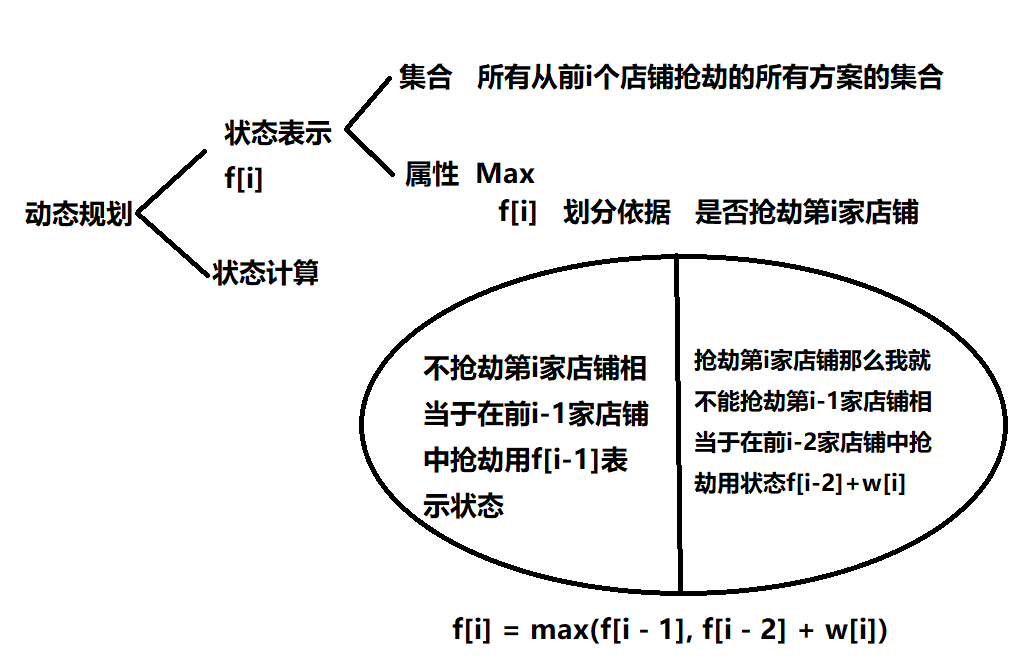
#include<iostream>
#include<cstring>

using namespace std;

const int N = 1e5 + 10;

int f[N], n, T;

int main()
{
    cin >> T;
    while(T --){
        memset(f, 0, sizeof f);
        cin >> n;
        int v;
        cin >> v;
        f[1] = v;
        for(int i = 2; i <= n; i ++){
            cin >> v;
            f[i] = max(f[i - 1], f[i - 2] + v);
        }
        cout << f[n] << endl;
    }

    return 0;
}

3.png 

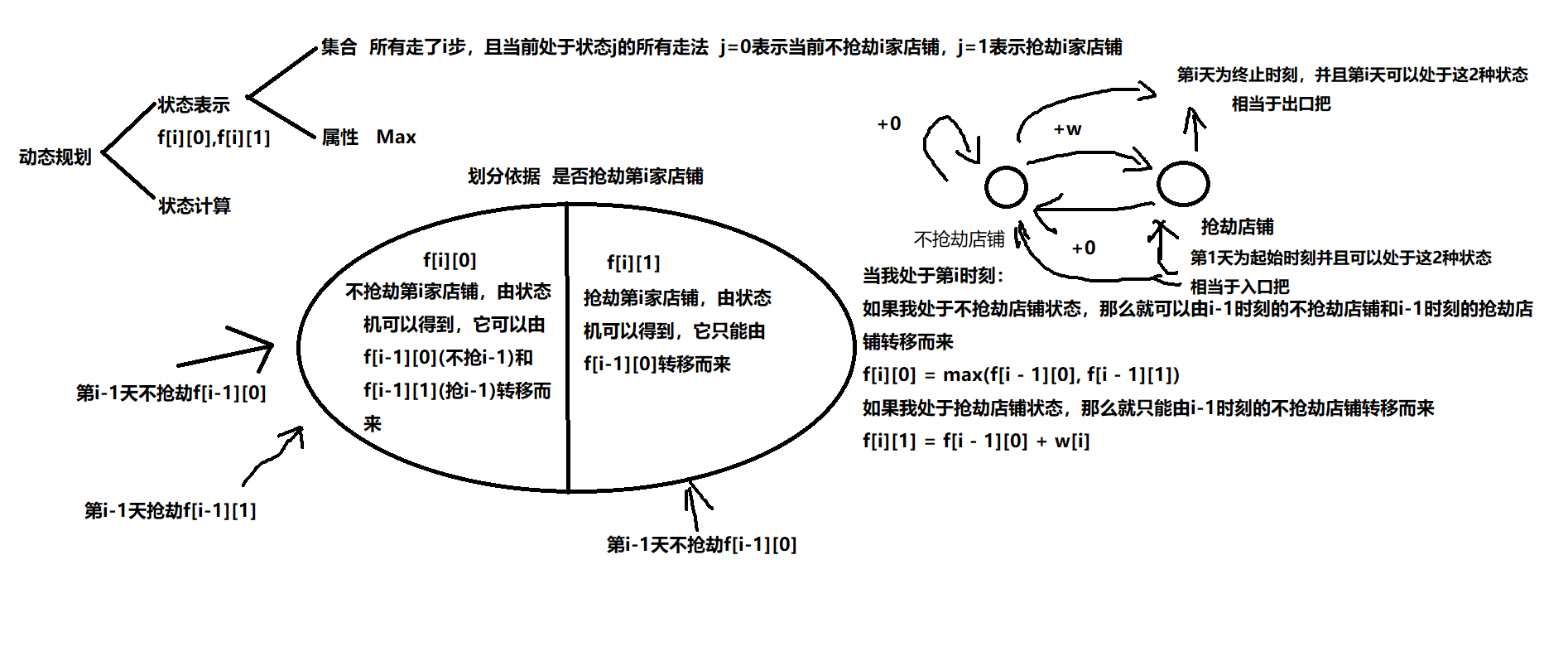
#include<iostream>
#include<cstring>

using namespace std;

const int N = 1e5 + 10, inf = 0x3f3f3f3f;

int n, f[N][2];

int main()
{
    int T;
    cin >> T;
    while(T -- ){
        cin >> n;
        memset(f, 0, sizeof f);
        f[0][0] = 0, f[0][1] = -inf;
        for(int i = 1; i <= n; i ++){
            int v;
            cin >> v;
            f[i][0] = max(f[i - 1][0], f[i - 1][1]);
            f[i][1] = f[i - 1][0] + v;
        }
        cout << max(f[n][1], f[n][0]) << endl;
    }

    return 0;
}

股票买卖 IV

4.png 

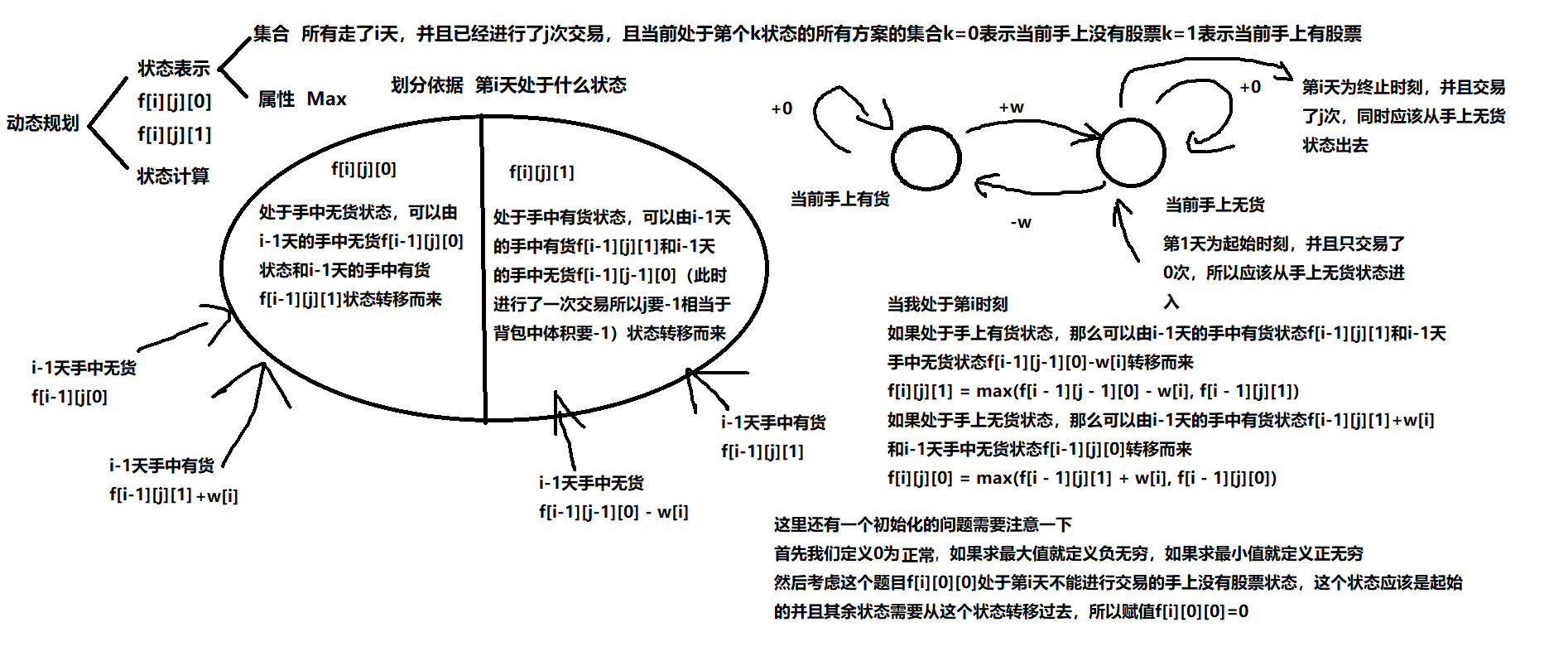
#include<iostream>
#include<cstring>

using namespace std;

const int N = 1e5 + 10, M = 110;

int f[N][M][3], n, m;

int main()
{
    scanf("%d%d", &n, &m);
    memset(f, -0x3f, sizeof f);
    for(int i = 0; i <= n; i ++)    f[i][0][0] = 0;

    for(int i = 1; i <= n; i ++){
        int v;
        cin >> v;
        for(int j = 1; j <= m; j ++){
            f[i][j][0] = max(f[i - 1][j][0], f[i - 1][j][1] + v);
            f[i][j][1] = max(f[i - 1][j][1], f[i - 1][j - 1][0] - v);
        }
    }
    int res = 0;
    for(int i = 0; i <= m; i ++)    res = max(res, f[n][i][0]);
    cout << res << endl;

    return 0;
}

股票买卖 V

5.png 

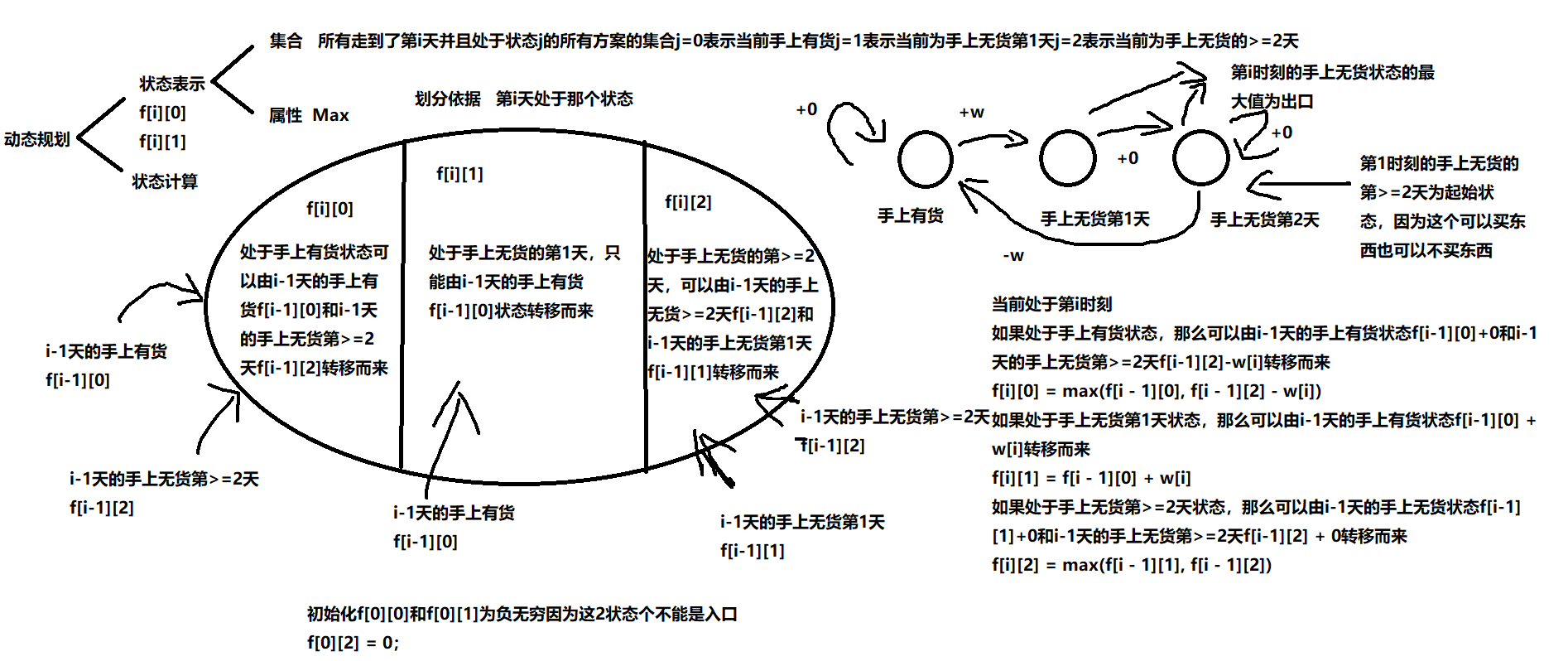
#include<iostream>
#include<cstring>

using namespace std;

const int N = 1e5 + 10, inf = 0x3f3f3f3f;

int f[N][3], n;

int main()
{
    cin >> n;
    f[0][0] = -inf, f[0][1] = -inf;
    f[0][2] = 0;

    for(int i = 1; i <= n; i ++){
        int v;
        cin >> v;
        f[i][0] = max(f[i - 1][0], f[i - 1][2] - v);
        f[i][1] = f[i - 1][0] + v;
        f[i][2] = max(f[i - 1][2], f[i - 1][1]);
    }
    cout << max(f[n][1], f[n][2]) << endl;

    return 0;
}

设计密码

emmm…先谢谢高大佬的kmp题解和y总的视频课

6.png 

emmm...上面就看了一下状态表示怎么做。

7.png 

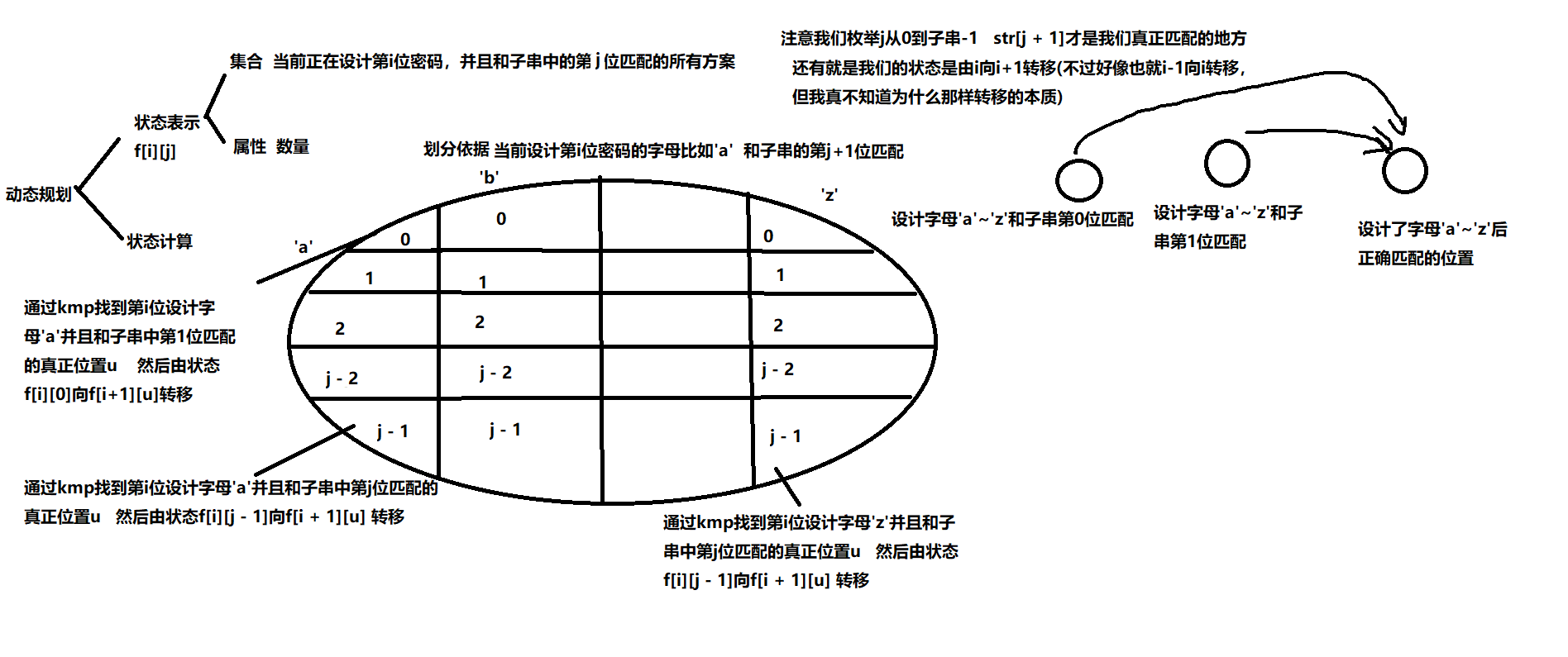
emmm...说实话，我画完图之后还是没搞清楚(太弱了)所以我要跑了一遍了样例

8.png 

emmm...最后我发现就是有一种状态就是f[i][j](j > i 的时候一定要是0因为这有i位密码要和j(>=i)进行匹配是不可能的...(我太笨了)
如果j == i 说明第i位密码和第j位子串匹配上了就一定等于1
如果j < i (j > 0)说明第i位密码和第j位子串那么就会有26^(i-j)但同时要注意减去当其中的某一种情况出现完全包含子串的时候
如果j==0就是所有方案减去上述的方案
还有就是通过Kmp找到正确的位置U
还有就是再多跑一次i=3的时候发现f[4][3] = 26   方案中cbc ('a' ~ 'b' + 'd' ~ 'z')这里面的25种方案没有统计上

#include<iostream>
#include<cstring>
#include<cstdio>
#include<algorithm>

using namespace std;

const int N = 55, mod = 1e9 + 7;

int f[N][N], n, m;
char s[N];
int ne[N];

int main()
{
    cin >> n >> s + 1;
    m = strlen(s + 1);
    for(int i = 2, j = 0; i <= m; i ++){
        while(j && s[i] != s[j + 1])    j = ne[j];
        if(s[i] == s[j + 1])    j ++;
        ne[i] = j;
    }

    f[0][0] = 1;
    for(int i = 0; i < n; i ++)
        for(int j = 0; j < m; j ++){
            for(int k = 'a'; k <= 'z'; k ++){
                int u = j;
                while(u && k != s[u + 1])   u = ne[u];
                if(s[u + 1] == k)   u ++;
                f[i + 1][u] = (f[i + 1][u] + f[i][j]) % mod;
            }
        }

    int res = 0;
    for(int i = 0; i < m; i ++) res = (res + f[n][i]) % mod;
    cout << res << endl;

    return 0;
}

修复DNA

emmmm…还不会ac自动机，下次补把。。。

2)状态压缩dp

emmm…还是先感谢y总的视频课

在我们的状态非常不好表示的时候，我们就可以用状态压缩啦

emmmm...状态压缩dp把，1、状态的考虑、表示和压缩2、就是动态规划
1)状态压缩
考虑状态的表示通常需要保存一定的状态数据(一种状态需要对应一种数据值)同时每个状态数据可以分解成许多数据单元
通常情况下每个状态数据可以通过一个整数来表示同时将这个整数分解成二进制形式。
比如在一行棋盘的格子上放棋子，在格子上放棋子表示1不放棋子表示0。
这样用0或者1来表示状态数据的每个单元，而整个状态数据就是一个一串0和1组成的二进制数。 
通常这样的状态数据实现为一个基本的数据类型或者一种哈希值，同时需要注意的是状态数据中的每个单元不能太多。
运算名 符号 效果
& 按位与 如果两个相应的二进制位都为1，则该位的结果值为1，否则为0
l 按位或 两个相应的二进制位中只要有一个为1，该位的结果值为1
^ 按位异或 若参加运算的两个二进制位值相同则为0，否则为1
~ 取反 ~是一元运算符，用来对一个二进制数按位取\反，即将0变1，将1变0
<< 左移 用来将一个数的各二进制位全部左移N位，右补0
*>> 右移 将一个数的各二进制位右移N位，移到右端 的低位被舍弃，对于无符号数，高位补0 
还有一些位操作
获得数x最右边的1   lowbit(x) = x & -x
获得第i位的数据     x >> i
设置第i位为1     x = (x | (1 << i))
设置第i位为0     x = (x & (~(1 << i)))
第i位取反        x = (x ^ (1 << i))

然后就是第二个:动态规划   这个应该不用多说了y总的闫式dp分析法了
然后就是需要注意状态内部的约束、状态和状态之间的约束关系
通常状态内部的约束可以先通过预处理来将满足条件的先筛选出来，以减小状态转移的时候运算量。
再就是状态和状态之间的约束关系则需要通过动态规划等来确定
比如计算到i时刻的a状态时，同时根据动态规划确定还需要用到前i-1行的状态，则需要枚举i-1行的状态，如果不满足约束条件就是可行的转移
再就是可以先预处理出状态与状态之间的联系，那些状态之间是满足约束关系，那些状态之间是不满足约束关系，可以先预处理。

棋盘式

骑士

emmm…先康康这个状态表示把

9.png

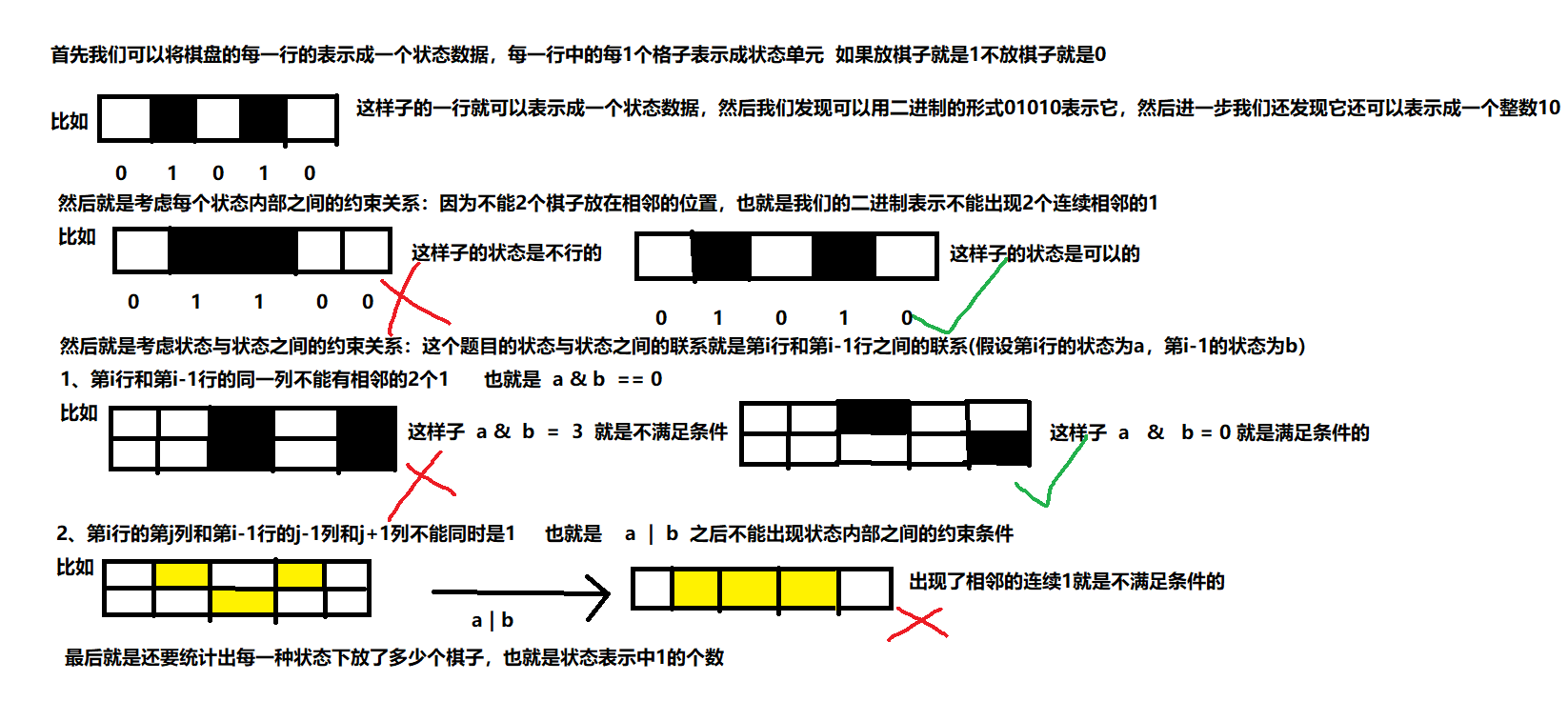
emmm…然后就是y总的闫式dp分析法了

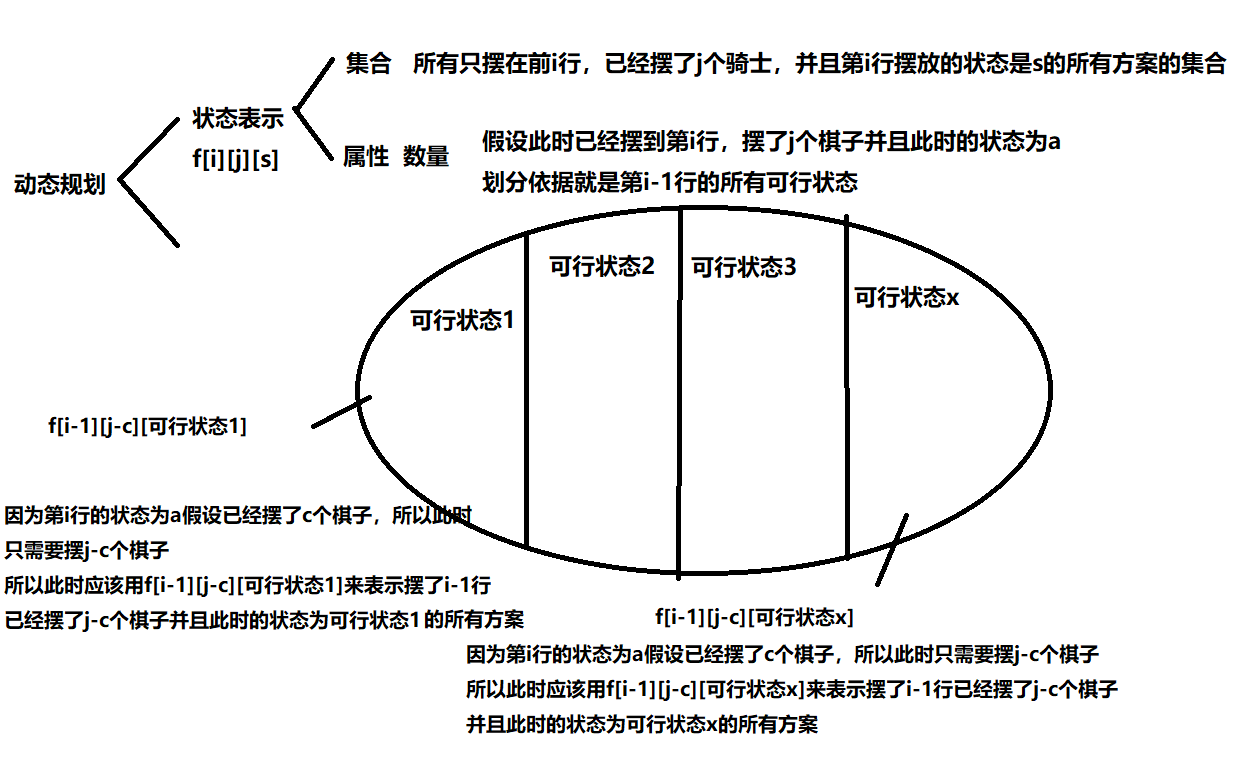
10.png 

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<vector>

using namespace std;

const int N = 12, M = 1 << 11;

long long f[N][110][M];
int n, m, cnt[M];
vector < int > st, h[M];

bool check(int st)
{
    for(int i = 0; i < n; i ++)
        if((st >> i & 1) && (st >> i + 1 & 1))
            return false;
    return true;
}

int count(int st)
{
    int res = 0;
    for(int i = 0; i < n; i ++) res += (st >> i & 1);
    return res;
}

int main()
{
    cin >> n >> m;

    for(int i = 0; i < 1 << n; i ++)// 预处理出状态的内部关系和每个状态中1的个数
        if(check(i)){
            st.push_back(i);
            cnt[i] = count(i);
        }

    for(int i = 0; i < st.size(); i ++)// 预处理出状态与状态之间的联系
        for(int j = 0; j < st.size(); j ++){
            int a = st[i], b = st[j];
            if((a & b) == 0 && check(a | b))
                h[i].push_back(j);
        }

    f[0][0][0] = 1;
    for(int i = 1; i <= n + 1; i ++)
        for(int j = 0; j <= m; j ++)
            for(int k = 0; k < st.size(); k ++)
                for(int u = 0; u < h[k].size(); u ++){
                    int c = cnt[st[k]];
                    if(j >= c)
                        f[i][j][k] += f[i - 1][j - c][h[k][u]];
                }
    cout << f[n + 1][m][0];

    return 0;
}

玉米田

emmm…还是先康一康这个状态转移方程

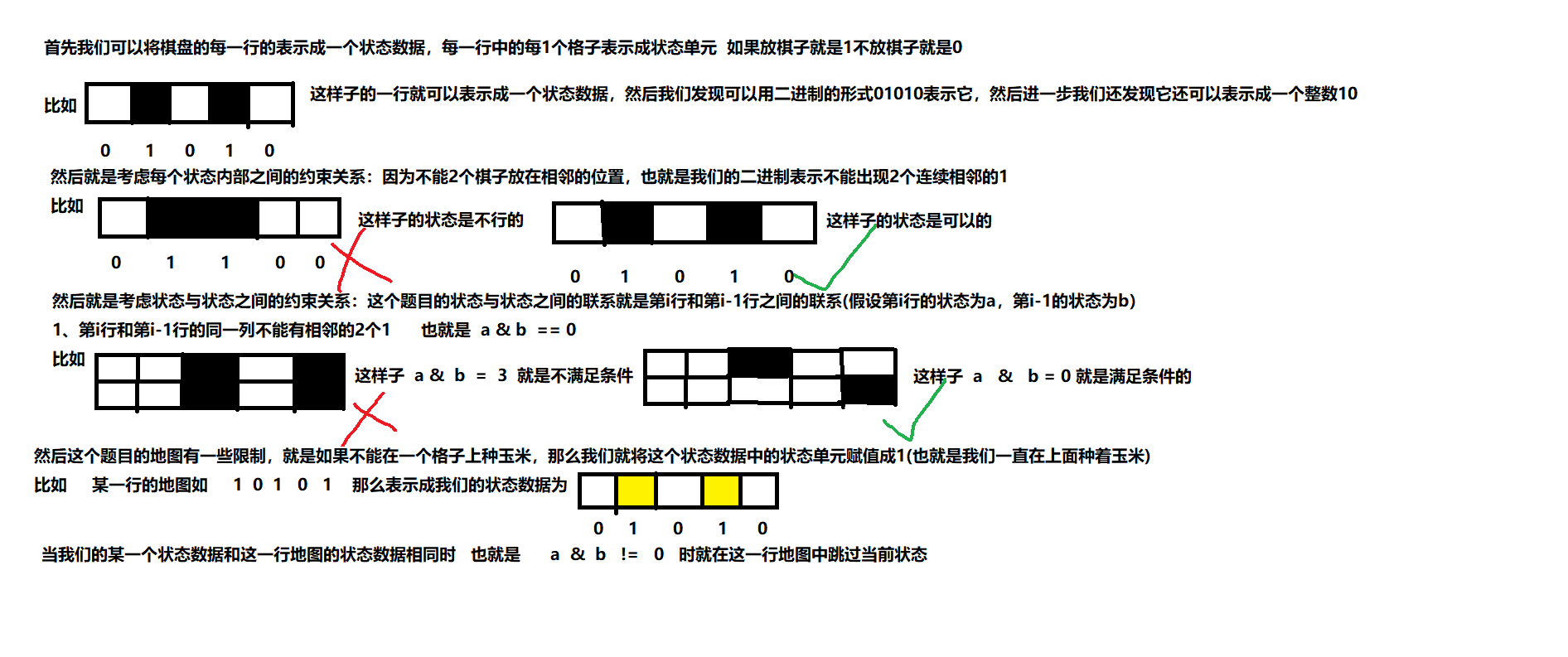
11.png

emmm…然后就是y总的闫式dp分析法了

12.png 

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<vector>

using namespace std;

const int N = 15, M = 1 << 11, mod = 1e8;

int n, m, f[N][M], g[N];
vector < int > st, h[M];

bool check(int st)
{
    for(int i = 0; i < m; i ++)
        if((st >> i & 1) && (st >> i + 1 & 1))
            return false;
    return true;
}

int main()
{
    cin >> n >> m;
    for(int i = 1; i <= n; i ++)
        for(int j = 0; j < m; j ++){
            int c;
            cin >> c;
            g[i] += !c << j;
        }

    for(int i = 0; i < 1 << m; i ++)
        if(check(i))
            st.push_back(i);

    for(int i = 0; i < st.size(); i ++)
        for(int j = 0; j < st.size(); j ++){
            int a = st[i], b = st[j];
            if((a & b) == 0)
                h[i].push_back(j);
        }

    f[0][0] = 1;
    for(int i = 1; i <= n + 1; i ++)
        for(int j = 0; j < st.size(); j ++)
            for(int k = 0; k < h[j].size(); k ++){
                if((st[j] & g[i])) continue;
                f[i][j] = (f[i][j] + f[i - 1][h[j][k]]) % mod;
            }
    cout << f[n + 1][0];

    return 0;
}

炮兵阵地

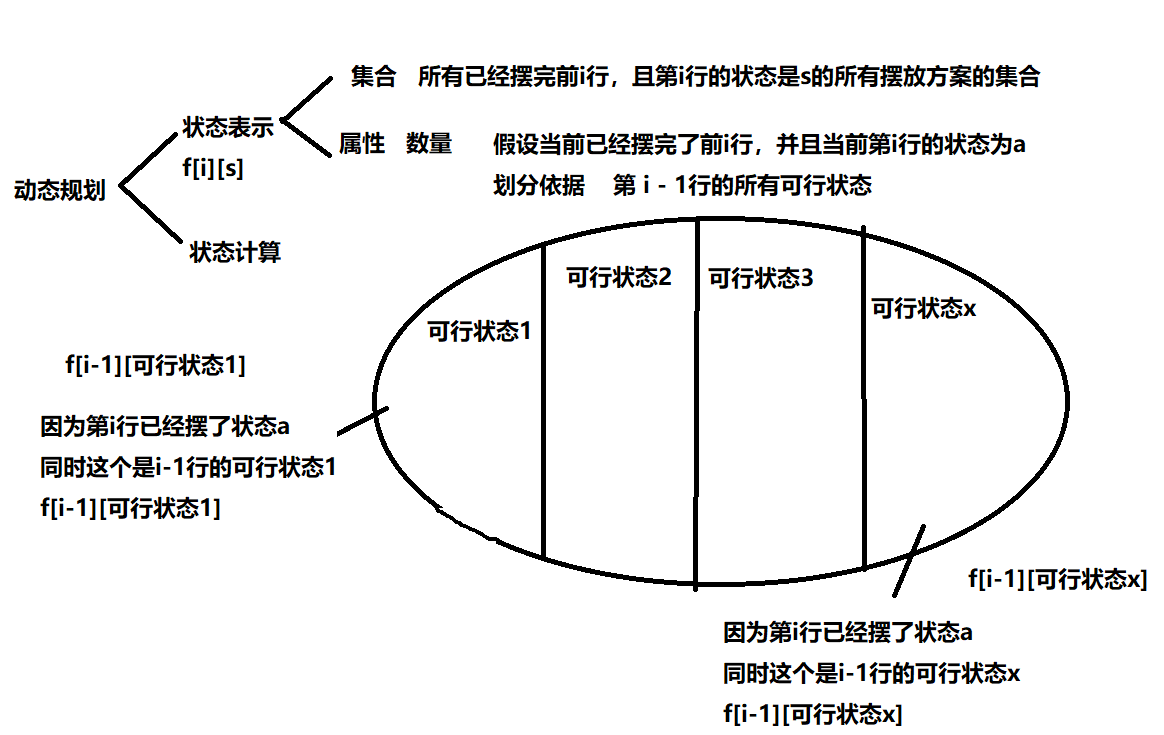
emmm…先看看这个状态表示把

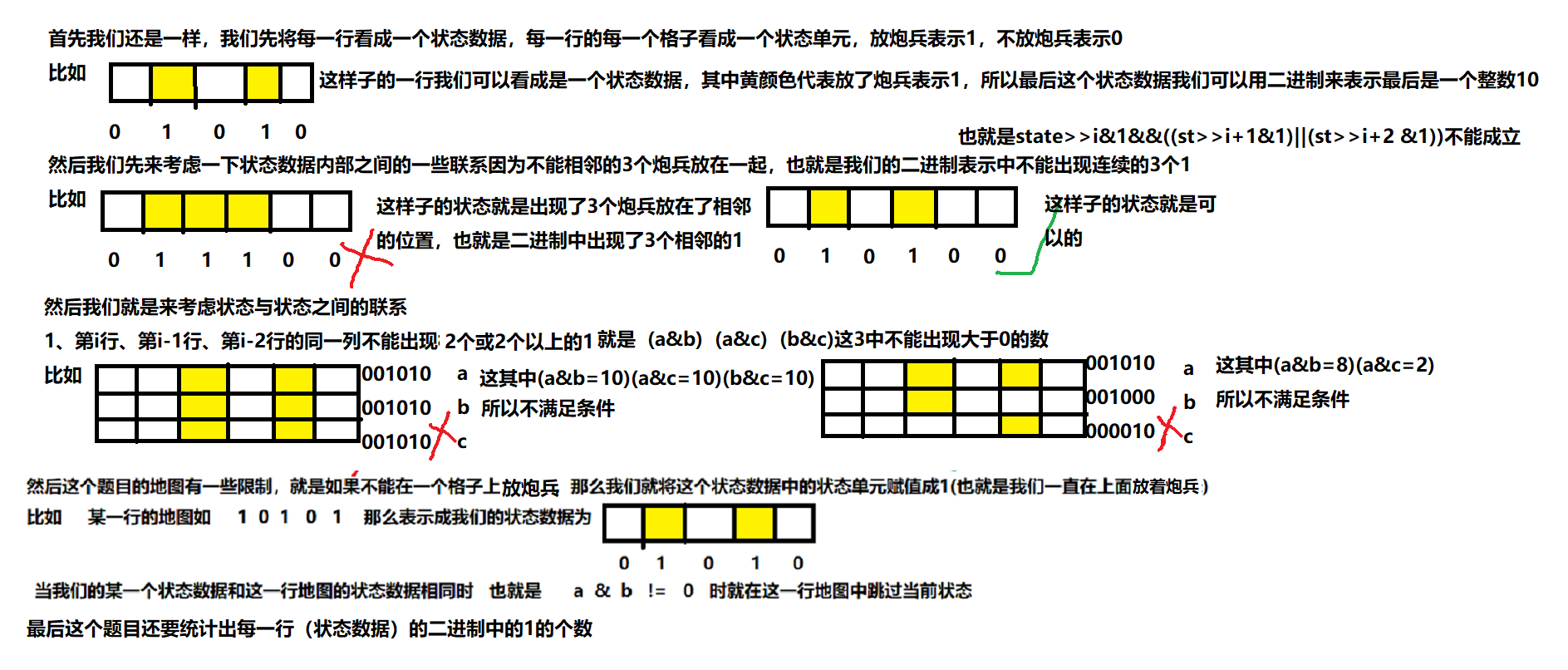
13.png

emmm…然后就是y总的dp分析法了

14.png 

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<vector>

using namespace std;

const int N = 110, M = 1 << 11;

int f[2][M][M], n, m, cnt[M], g[N];
vector < int > st;

bool check(int st)
{
    for(int i = 0; i < m; i ++)
        if((st >> i & 1) && ((st >> i + 1 & 1) || (st >> i + 2 & 1)))
            return false;
    return true;
}

int count(int st)
{
    int res = 0;
    for(int i = 0; i < m; i ++) res += (st >> i & 1);
    return res;
}

int main()
{
    cin >> n >> m;
    for(int i = 1; i <= n; i ++)
        for(int j = 0; j < m; j ++){
            char c;
            cin >> c;
            if(c == 'H')    g[i] += 1 << j;
        }

    for(int i = 0; i < 1 << m; i ++)
        if(check(i)){
            st.push_back(i);
            cnt[i] = count(i);
        }

    for(int i = 1; i <= n + 2; i ++)
        for(int j = 0; j < st.size(); j ++)
            for(int k = 0; k < st.size(); k ++)
                for(int u = 0; u < st.size(); u ++){
                    int a = st[j], b = st[k], c = st[u];
                    if((a & b) || (a & c) || (b & c))   continue;
                    if((g[i] & a) || (g[i - 1] & b))    continue;
                    f[i & 1][k][j] = max(f[i & 1][k][j], f[i - 1 & 1][u][k] + cnt[a]);
                }
    cout << f[n + 2 & 1][0][0] << endl;

    return 0;
}

愤怒的小鸟

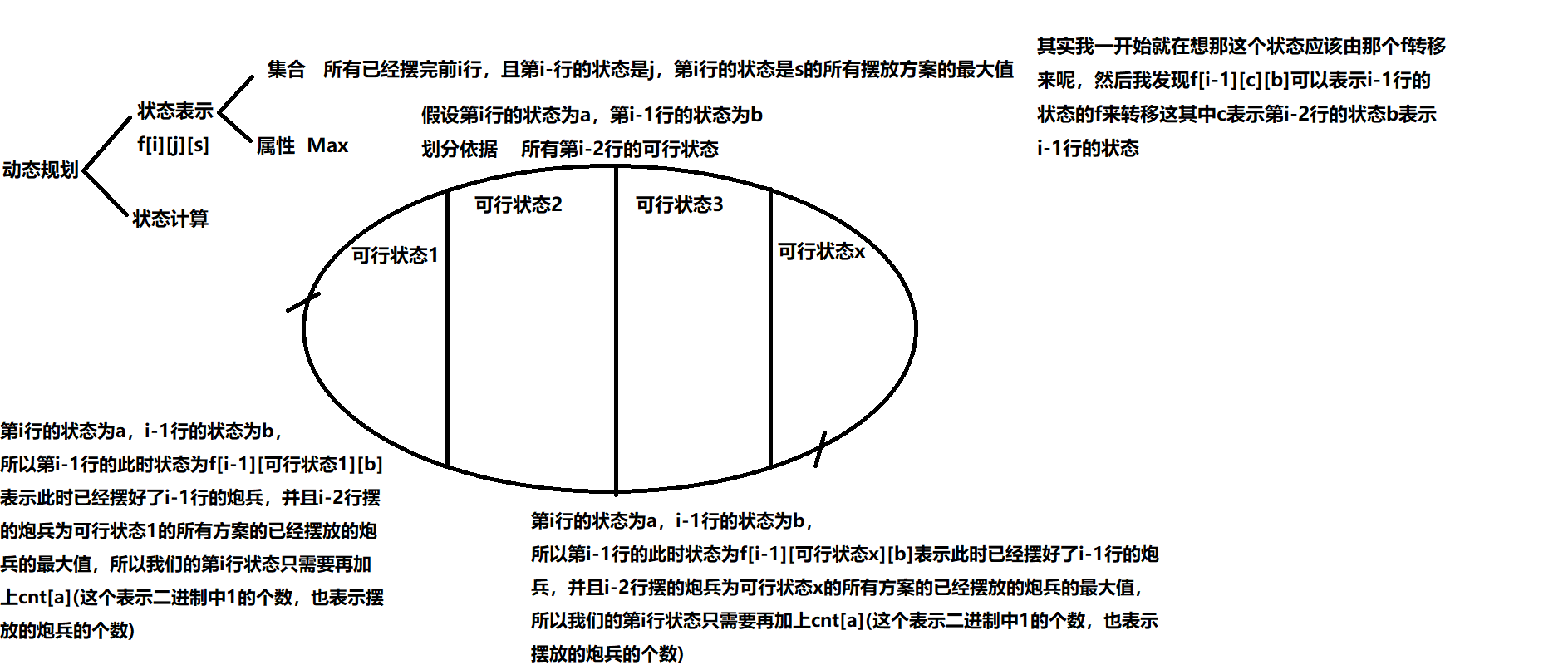
emmm…先看下状态表示把

15.png

emmm…一下的dp分析法纯属个人理解，如果有更好的，请大佬告诉本蒟蒻把

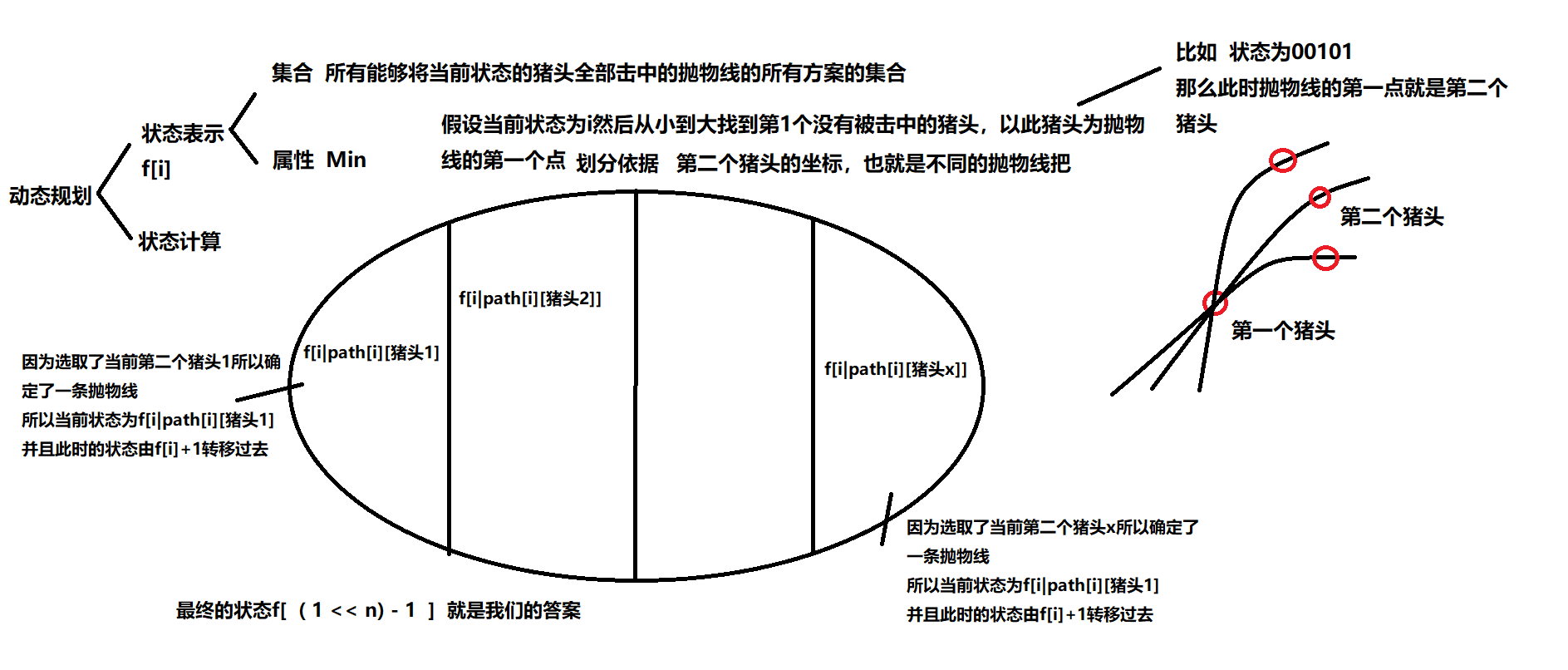
16.png 

#include <cstring>
#include <iostream>
#include <algorithm>
#include <cmath>
#include<bitset>

#define x first
#define y second

using namespace std;

typedef pair<double, double> PDD;

const int N = 18, M = 1 << 18;
const double eps = 1e-8;

int n, m;
PDD q[N];
int path[N][N];
int f[M];

int cmp(double x, double y)
{
    if (fabs(x - y) < eps) return 0;
    if (x < y) return -1;
    return 1;
}

int main()
{
    int T;
    cin >> T;
    while (T -- )
    {
        cin >> n >> m;
        for (int i = 0; i < n; i ++ ) cin >> q[i].x >> q[i].y;

        memset(path, 0, sizeof path);
        for (int i = 0; i < n; i ++ )
        {
            path[i][i] = 1 << i;// 表示只选取一个猪头
            for (int j = 0; j < n; j ++ )
            {
                double x1 = q[i].x, y1 = q[i].y;
                double x2 = q[j].x, y2 = q[j].y;
                if (!cmp(x1, x2)) continue;// 如果2个猪头在同一列就跳过
                double a = (y1 / x1 - y2 / x2) / (x1 - x2);
                double b = y1 / x1 - a * x1;

                if (cmp(a, 0) >= 0) continue;// 如果开头向上也跳过
                int state = 0;
                // cout << i << " " << j << " " << a << " " << b << " ---- " << endl;
                for (int k = 0; k < n; k ++ )// 加上这条抛物线能够击中的猪头
                {
                    double x = q[k].x, y = q[k].y;
                    // cout << x << " " << y << " --- " << endl;
                    // cout << a * x * x + b * x << " " << y << " -- " << endl;
                    if (!cmp(a * x * x + b * x, y)) state += 1 << k;
                }
                path[i][j] = state;
                // cout << bitset<16>(path[i][j]) << endl;
            }
        }

        memset(f, 0x3f, sizeof f);
        f[0] = 0;
        for (int i = 0; i + 1 < 1 << n; i ++ )
        {

            int x = 0;
            for (int j = 0; j < n; j ++ )// 找到此时的状态的第一个猪头
                if (!(i >> j & 1))
                {
                    x = j;
                    break;
                }


            for (int j = 0; j < n; j ++ ){
                // cout << i << " " << x << " --- " << j << " " << bitset<16>(i | path[x][j]) << " " << f[i] << " " << f[i | path[x][j]] << " ----- ";
                f[i | path[x][j]] = min(f[i | path[x][j]], f[i] + 1);
                // cout << i << " " << x << " --- " << j << " " << bitset<16>(i | path[x][j]) << " " << f[i] << " " << f[i | path[x][j]] << endl;
            }
        }

        cout << f[(1 << n) - 1] << endl;
    }

    return 0;
}

宝藏

emmm…下次补把

5 评论

用户头像
二助   2020-02-11 09:53         踩      回复

前排资瓷

用户头像
豆浆灬油条   2020-02-11 12:02         踩      回复

emmm…我其实还怕我这个蒟蒻误导人的

用户头像
fchunwww   2020-02-11 09:41         踩      回复

大佬 你知道秦大佬的b站id么 找不到了......

用户头像
豆浆灬油条   2020-02-11 12:08         踩      回复

大佬 我也不知道唉 不好意思哈

用户头像
fchunwww   2020-02-11 12:21    回复了 豆浆灬油条 的评论         踩      回复

没事没事