acwing998
暴力 O(n∗m)
由于可以选择初始攻击力,直接将初始攻击力从0枚举到m,每一次攻击力进行位运算,最后取最大值即可
时间复杂度
暴力需要外层枚举m次,内层每次需要进行位运算n次,总共时间复杂度为O(m∗n)
该题时间为1s,最大数据量为10^9*10^5,暴力算法肯定超时
位运算优化 O(logm∗m)
二进制位运算最大的特点在于每次计算之后没有进位与借位,每一位计算的时候都是独立计算
根据独立计算可得,我们可以确定攻击的二进制的每一位,自然而然就确定答案的每一位了
如何确定攻击的每一位填1还是填0
填1必须满足:
- 该位为1了以后总和不能大于最大的攻击力
- 填1了之后运算过后答案的二进制位上还是1
其余情况要么填1不会比填0更优,要么填1大于了m,这种情况下显然填0更好
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<cmath>
using namespace std;
const int N=1e5+10;
pair<string,int> a[N];
int n,m;
int cal(int x,int k)
{
for(int i=1;i<=n;i++)
{
int t=a[i].second>>x & 1;
if(a[i].first == "AND") k&=t;
else if(a[i].first == "OR") k|=t;
else k^=t;
}
return k;
}
int main()
{
//cout<<log2(1e9)<<endl;
cin>>n>>m;
for(int i=1;i<=n;i++)
cin>>a[i].first>>a[i].second;
int val=0,ans=0;
for(int i=29;i>=0;i--)
{
int t0=cal(i,0);
int t1=cal(i,1);
if(val + (1<<i) <= m && t1 > t0)
val+=1<<i,ans+=t1<<i;
else
ans+=t0<<i;
}
cout<<ans<<endl;
return 0;
}
棋盘类(基于连通性)状压dp
1.十字型
输入样例:
2 3
1 1 1
0 1 0
输出样例:
9
用二进制数来描述一行中方格的状态,1表示种玉米,0表示不种玉米
样例第一行有以下5种种玉米的方案

根据题意,把每一行的状态用二进制的数表示,0代表不在这块放牛,1表示在这一块放牛。首先很容易看到,每一行的状态要符合牧场的硬件条件,即牛必须放在能放牧的方格上。这样就能排除一些状态。另外,牛与牛之间不能相邻,这样就要求每一行中不能存在两个相邻的1,这样也能排除很多状态。然后就是根据上一行的状态转移到当前行的状态的问题了。必须符合不能有两个1在同一列(两只牛也不能竖着相邻)的条件。这样也能去掉一些状态。然后,上一行的所有符合条件的状态的总的方案数就是当前行该状态的方案数。
(1)初始化所有合法状态,即找没有相邻1的二进制数。用state[]存储合法状态
(2)枚举不同合法状态之间的转移关系,只要a&b == 0,状态a就可转到b

#include<iostream>
#include<vector>
#include<bitset>
using namespace std;
const int N=15,M=1<<12,mod=1e8;
int f[N][M];
int g[N];
int n,m;
vector<int> state;
vector<int> head[M];
bool check(int state)//判断相邻两列
{
if(state & state<<1)
return false;
return true;
}
int main()
{
cin>>n>>m;
for(int i=1;i<=n;i++)
for(int j=0;j<m;j++)
{
int x;
cin>>x;//若x为1,表示玉米田不可用
g[i]+=!x<<(m-1-j);
}
for(int i=0;i<1<<m;i++)
if(check(i))
state.push_back(i);//所有合法状态
f[0][0]=1;//边界
for(int i=1;i<=n+1;i++)//枚举到第n+1行,省略求和
for(int a=0;a<state.size();a++)//第i行状态为a,i-1行状态为b
for(int b=0;b<state.size();b++)
{
if((g[i] & state[a]) == 0 && (state[a] & state[b]) == 0) //不与上一行冲突,且不能在地图上0的地方种玉米
f[i][a]=(f[i][a]+f[i-1][b])%mod;
}
cout<<f[n+1][0]<<endl;
return 0;
}
炮兵阵地
状态:f[i][j][k],已经摆完前i行,第i行状态是j,第i-1行状态是k的摆放方案
属性: max
划分依据,
第i行状态不仅和第i-1行状态有关,还和第i-2行状态有关,所有f[i][j][k]第i行状态是j,第i-1行状态是k,依据i-2行状态来划分。
a表示第i行状态,b表示第i-1行状态,c表示第i-2行状态
要求:
(1)每行的意大利炮不能相互攻击到,((a & b) || (a & c) || (a & b))==0
(2)意大利炮只能放在平地上,(g[i] & a )||(g[i-1] & b),无需判断g[i-2]行,若g[i-2]行意大利炮放到了山地上属于不合法状态,一定为0


#include<iostream>
#include<vector>
using namespace std;
const int N=110,M=1<<10;//n的范围远大于m的范围,以列作为枚举的状态
int g[N];
int cnt[M];//状态对应的1的个数
vector<int> state;
int n,m;
int f[2][M][M];//f[i,j,k] 第i行状态是j,第i-1行状态是k
bool check(int state)
{
if((state & state<<1) || (state & state<<2))
return false;
return true;
}
int count(int state)
{
int res=0;
for(int i=0;i<m;i++)
if(state>>i &1)
res++;
return res;
}
int main()
{
cin>>n>>m;
for(int i=1;i<=n;i++)
for(int j=0;j<m;j++)
{
char c;
cin>>c;
if(c == 'H')
g[i]+=1<<(m-1-j);
}
for(int i=0;i<1<<m;i++)
{
if(check(i))
{
state.push_back(i);
cnt[i]=count(i);
}
}
//f[i,j,k] 已经摆完前i行,第i行状态是j,第i-1行状态是k
for(int i=1;i<=n+2;i++)
for(int j=0;j<state.size();j++)
for(int k=0;k<state.size();k++)
for(int u=0;u<state.size();u++)
{
int a=state[j],b=state[k],c=state[u];//a表示第i行状态,b表示第i-1行状态,c表示第i-2行状态
if((a & b) || (a & c) || (a & b))//相邻两行不能相互攻击到
continue;
if((g[i] & a )||(g[i-1] & b))//意大利炮不能放山地上
continue;
f[i&1][a][b]=max(f[i&1][a][b],f[i-1&1][b][c]+cnt[a]);
}
cout<<f[n+2&1][0][0]<<endl;
return 0;
}
2.井字型
骑士
状态:f[i][j][k],已经摆完前i行,第i行摆放状态是j(二进制位为1表示摆放,0表示不摆),已经摆了k个
属性:count
状态划分:
要求:国王不能左右相邻,不能上下相邻,不能对角相邻,第i行状态为a,i-1行状态为b
(1)每行内部不能有两个1相邻,(预处理)
(2)第i行和第i-1行状态不能相互攻击到,(a & b) == 0 ,a|b不能有两个相邻的1
//第i行状态只跟第i-1行状态有关
#include<iostream>
#include<vector>
using namespace std;
const int N=12,M=1<<10,K=110;
typedef long long LL;
LL f[N][M][K];
vector<int> state;
int cnt[M];//每个状态对应1的数目
int n,m;
bool check(int state)
{
for(int i=0;i<n;i++)
{
if((state>>i &1) && (state>>i+1 &1))
return false;
}
return true;
}
int count(int state)
{
int res=0;
for(int i=0;i<n;i++)
res+=state>>i &1;
return res;
}
int main()
{
cin>>n>>m;
for(int i=0;i<1<<n;i++)//如果满足左右互不相邻,则存储当前状态
if(check(i))
{
state.push_back(i);
cnt[i]=count(i);
}
//cout<<state.size()<<endl;
f[0][0][0]=1;
for(int i=1;i<=n+1;i++)
for(int a=0;a<state.size();a++)
for(int k=0;k<=m;k++)
for(int b=0;b<state.size();b++)
{
int sa=state[a],sb=state[b];//sa表示第i行状态,sb表示第i-1行状态
if((sa & sb) == 0 && check(sa|sb))
{
int c=cnt[sa];
//cout<<sa<<' '<<sb<<' '<<k<<' '<<c<<endl;
if(k>=c)
f[i][sa][k]+=f[i-1][sb][k-c];
}
}
cout<<f[n+1][0][m]<<endl;
return 0;
}
3.插头型
蒙德里安的梦想
考虑决策——骨牌的放法:横着 或者 竖着。
如果横着:
需要两个连续的空位,并且上一行的这两个位置也得已经被覆盖。
如果竖着:
(a) 上一行对应的位置是空的,我们把那个空填上。
(b) 上一行对应的位置是被覆盖的,那么我们把这一行的位置设为空,表示下一行的对应位置必须竖放,填上这块空白
状态表示:f[i][j],表示第i行的形态为j时的摆放方案数量
j是用十进制记录的m位二进制数,其中第k(0<=k<m)位为1表示第k列是一个竖着的1*2的长方形的上面一半。
记第i-1行状态为k,第i行状态为j
k能转移到j,当且仅当:
(1)j和k执行按位与为0,保证每个数字1下必须是0,才得以补全12的长方形
(2)j和k执行按位或的结果,连续的0必须是偶数。这些0表示若干横着的12长方形,奇数个0无法满足这种摆放形态。
可以预处理出[0,$2^{m}$-1]内所有满足连续的0必须是偶数的整数
#include<bits/stdc++.h>
using namespace std;
const int N = 12, M = 1 << N;
int st[M];
long long f[N][M];
int main()
{
int n, m;
while (cin >> n >> m && n)
{
for (int i = 0; i < 1 << m; i ++)
{
int cnt = 0;// cnt 为当前已经存在多少个连续的0
st[i] = true;
for (int j = 0; j < m; j ++)
if (i >> j & 1)
{
if (cnt & 1) //当前位为1,上一段连续为0的位置已结束
st[i] = false;
cnt = 0;
}
else cnt ++;
if (cnt & 1) st[i] = false; // 扫完后要判断一下最后一段有多少个连续的0
}
memset(f, 0, sizeof f);
f[0][0] = 1;
for (int i = 1; i <= n; i ++)
for (int j = 0; j < 1 << m; j ++)
for (int k = 0; k < 1 << m; k ++)
if ((j & k) == 0 && (st[j | k]))
// j & k == 0 表示 i 行和 i-1 行不能同时捅出来
// st[j | k] == 1 表示 在 i 列状态 j, i - 1 列状态 k 的情况下(连续的0必须有偶数个)是合法的.
f[i][j] += f[i - 1][k];
cout << f[n][0] << endl;
}
return 0;
}
集合类(每个元素是否在集合里面)状压dp
最短Hamilton路径
给定一张 n 个点的带权无向图,点从 0~n-1 标号,求起点 0 到终点 n-1 的最短Hamilton路径。 Hamilton路径的定义是从 0 到 n-1 不重不漏地经过每个点恰好一次。
状态表示:dp[i][j] :所有从0走到j,走过的所有点的状态是i的最短路径
状态划分:
dp[i][j]表示所有从0走到j,当前已经走过点的为i的集合。所以这个状态转移方程就是找一个中间点k,将已经走过点的集合i中去除掉j(表示j不在经过的点的集合中),然后再加上从k到j的权值。问题在于如何表达已经走过点的集合i,其实很简单,假如走过0,1,4这三个点,我们用二进制10011就可以表示,2,3没走过所以是0。
那么走过点的集合i中去除掉点j也很容易表示i - (1 << j),比方说i是{0,1,4},j是1,那么i = 10011,(1 << j) = 10,i - (1 << j) = 10001
那么问题的答案就应该是dp[01....111][n-1],表示0~n-1都走过,且当前移动到n-1这个点。
下时间复杂度:
n为20的时候,外层循环(1<<20),内层循环20,所以整体时间复杂度O($20∗2^{20}$),这比O(n∗n!)快多了
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 20, M = 1 << N;
int n;
int w[N][N];
int f[M][N];
int main()
{
cin >> n;
for (int i = 0; i < n; i ++ )
for (int j = 0; j < n; j ++ )
cin >> w[i][j];
memset(f, 0x3f, sizeof f);
f[1][0] = 0;//第一个点是不需要任何费用的
/*
注意循环顺序
如果反过来写,不能保证在f[i][j] = min(f[i][j], f[i - (1 << j)][k] + w[k][j])中右边的状态在左边的状态之前被计算出来。
*/
for (int i = 0; i < 1 << n; i ++ )//i代表着是一个方案集合,其中每一个位置1和0,代表着这个点经过还是没有经过
for (int j = 0; j < n; j ++ )//枚举当前到了哪一个点
if (i >> j & 1)//如果i集合中第j位是1,也就是到达过这个点
for (int k = 0; k < n; k ++ )//枚举到达j的点k
if (i >> k & 1)
f[i][j] = min(f[i][j], f[i - (1 << j)][k] + w[k][j]);
cout << f[(1 << n) - 1][n - 1];
return 0;
}
poj2288
题意:
给出n个点,m条边的无向图,给出每个点的点权,求点权和最小的哈密顿路径,相邻两个点要加上点权的乘积,形成环要加上环上的点权
这题先占个坑,以后补。。。。
hdu1074
题意:
给了n个家庭作业,然后给了每个家庭作业的完成期限和花费的实践,如果完成时间超过了期限,那么就要扣除分数,然后让你找出一个最优方案使扣除的分数最少,当存在多种方案时,输出字典序最小的那种,因为题意已经说了家庭作业的名字是按照字典序从小到大输入的,所以处理起来就好多了。
思路
在引出正解前,我们从DFS开始引入,如果这题用DFS来写,想必大家都有思路,很好理解。因为每个作业要么写,要么不写,因此开个布尔数组搜就行了,而且这题n <= 15;仔细想来,加点剪枝还是可以过的没准。
如果我们把布尔数组看成一个二进制位,进行状态压缩,很明显可以知道,最多只有2的15次方位的1二进制大小的状态。因此可以用2进制所对应的10进制来表示状态,这就是状态压缩。
状态表示:dp[i]记录完成作业状态为i时的最少损失的分数。
状态划分:
1.状态a能做第i号作业的条件是a中作业i尚未完成,即a&i=0。
2.若有两个状态dp[a],dp[b]都能到达dp[i],那么选择能使到达i扣分小的那一条路径,若分数相同,转入3
3.这两种状态扣的分数相同,那么选择字典序小的,由于作业按字典序输入,故即dp[i].pre = min(a,b);
最后dp[2^n-1]即为最少扣分,课程安排可递归的输出
#include <cstdio>
#include <algorithm>
#include <iostream>
#include <cstring>
#include <bitset>
using namespace std;
const int N=20,M=1<<15;
const int INF=0x3f3f3f3f;
struct
{
char sbj[110];
int deadline;
int fintime;
}w[N];
int dp[M];//dp[i]表示当前写作业状态是i的情况下被扣分的最小值
int pre[M];//记录前驱
int day[M];//记录当前写作业状态是i的情况下已经过了多少天
int n;
void print_path(int state)
{
if(state==0)return;
int t=0;
for(int i=0;i<n;i++)
if( (state&(1<<i))!=0 && (pre[state]&(1<<i))==0 )
{
t=i;
break;//按字典序最小输出,由于输入时已按字典序输入,找到第一个满足的break
}
print_path(pre[state]);
cout<<w[t].sbj<<endl;
}
int main()
{
int T;
scanf("%d",&T);
while(T--)
{
scanf("%d",&n);
for(int i=0;i<n;i++)
scanf("%s%d%d",&w[i].sbj,&w[i].deadline,&w[i].fintime);
memset(dp,0x3f,sizeof dp);
memset(day,0,sizeof day);
dp[0]=0;//当前还未做作业时被扣分为0
for(int i=0;i<1<<n;i++)
{
//cout<<(bitset<3>(i))<<" : "<<endl;
for(int j=0;j<n;j++)
{
if(i&(1<<j))continue;//第j位为1,表示第j位上的作业已完成,continue
int today=0;
// for(int k=0;k<n;k++)
// if(i&(1<<k))
// today+=w[k].fintime;
// today+=w[j].fintime;
today=day[i]+w[j].fintime;//today表示今天是第几天
int score=0;
if(today>w[j].deadline)
score=today-w[j].deadline;//完成日期与截止日期的差值 ,若差值<0,则不需扣分
if(dp[i|(1<<j)]>dp[i]+score)
{
dp[i|(1<<j)]=dp[i]+score;
day[i|1<<j]=day[i]+w[j].fintime;
//cout<<"--"<<(bitset<3>(i|(1<<j)))<<' '<<dp[i|(1<<j)]<<endl;
pre[i|(1<<j)]=i;
}
}
//cout<<endl;
}
printf("%d\n",dp[(1<<n)-1]);
print_path((1<<n)-1);
}
return 0;
}
旅行商问题(TSP),

TSP问题是NP难度的,没有多项式时间的高效算法。

假设最短的TSP路径是path=(v0->v1->v2->v3->v4->v0)
那么path=(v0->v1)+(v1->v2->v3->v0)
所以问题转变为:求经过所有城市的最短回路->从某个城市回到起点的最短路径
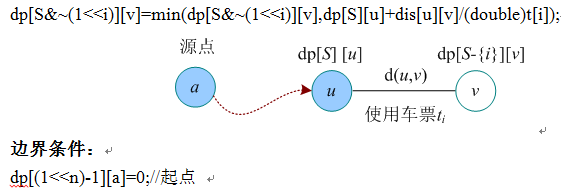
DP状态:假设已经访问过的城市集合是S(已访问为1,未访问为0),当前所在城市是u,用dp[S][u]表示从u出发访问剩余的所有城市最后回到起点的路径费用总和的最小值。
状态转移方程:
dp[S][u]=min(dp[S∪{v}][v]+dist(u,v)|v∉S}

临界条件如果递推的话是起点,递归的话是终点
#include<cstring>//递推,输出路径
#include<bitset>
#include<iostream>
#include<algorithm>
using namespace std;
const int INF=0x3f3f3f3f;
int dp[1<<15][15];//dp[S][u]:S表示已经过的节点,从u出发走完所有剩余顶点回到起点的最短距离
int g[15][15];
int path[1<<15][15];//最优路径
int n,m; //n个节点,m条边
void Init()
{
memset(dp,0x3f,sizeof(dp));
memset(g,0x3f,sizeof(g));
memset(path,-1,sizeof(path));
}
void Traveling()//计算dp[S][u]
{
dp[(1<<n)-1][0]=0;//注意:1<<n一定要加括号
for(int S=(1<<n)-2;S>=0;S--)
for(int u=0;u<n;u++)
for(int v=0;v<n;v++)
{//u可以等于0,起点0可看做已访问(从起点0出发回到起点0)
if((u!=0&&!(S>>u&1))||g[u][v]==INF) continue;,//若 u!=0,则u必须已访问
if(!(S>>v&1)&&dp[S][u]>dp[S|1<<v][v]+g[u][v])
{
dp[S][u]=dp[S|1<<v][v]+g[u][v];
cout<<"S="<<(bitset<5>(S))<<"\t u="<<u<<"\tv="<<v<<"\tdp["<<(bitset<5>(S))<<"]["<<u<<"]=";
cout<<"dp["<<(bitset<5>(S|1<<v))<<"]["<<v<<"]+"<<g[u][v]<<"="<<dp[S][u]<<endl;
path[S][u]=v;//记录后继节点
}
}
}
void print(int S,int u)//打印路径
{
if(S==(1<<n)-1) return;
int v=path[S][u];//u的后继v
cout<<"--->"<<v;
print(S|1<<v,v);//将v加入已走过的节点集合,再从v出发
}
int main()
{
int u,v,w;//u,v代表城市,w代表u和v城市之间路的长度
cin>>n>>m;
Init();
for(int i=0;i<m;i++)
{
cin>>u>>v>>w;
//g[u][v]=g[v][u]=w;//无向图
g[u][v]=w;//有向图
}
Traveling();
cout<<"最短路径: "<<0;
print(0,0);
cout<<endl;
cout<<"最短路径长度:"<<dp[0][0]<<endl;
return 0;
}

#include<cstring>//记忆化递归,输出路径
#include<bitset>
#include<iostream>
#include<algorithm>
using namespace std;
const int INF=0x3f3f3f3f;
int dp[1<<15][15];//dp[S][u]:S表示已经过的节点,从u出发走完所有剩余顶点回到起点的最短距离
int g[15][15];
int path[1<<15][15];//最优路径
int n,m; //n个节点,m条边
void Init()
{
memset(dp,-1,sizeof(dp));
memset(g,0x3f,sizeof(g));
memset(path,-1,sizeof(path));
}
int Traveling(int S,int u)//计算dp[S][u],记忆化递归
{
if(dp[S][u]>=0)
return dp[S][u];
if(S==(1<<n)-1&&u==0)
return dp[S][u]=0;//递归结束条件
int ans=INF;
for(int v=0;v<n;v++)
if(!(S>>v&1)&&g[u][v]!=INF)
{
int tmp=Traveling(S|1<<v,v)+g[u][v];
if(ans>tmp)
{
ans=tmp;
cout<<"S="<<(bitset<5>(S))<<"\t u="<<u<<"\tv="<<v<<"\tdp["<<(bitset<5>(S))<<"]["<<u<<"]=";
cout<<"dp["<<(bitset<5>(S|1<<v))<<"]["<<v<<"]+"<<g[u][v]<<"="<<ans<<endl;
path[S][u]=v;//记录后继节点
}
}
return dp[S][u]=ans;
}
void print(int S,int u)//打印路径
{
if(S==(1<<n)-1) return;
int v=path[S][u];//u的后继v
cout<<"--->"<<v;
print(S|1<<v,v);//将v加入已走过的节点集合,再从v出发
}
int main()
{
int u,v,w;//u,v代表城市,w代表u和v城市之间路的长度
cin>>n>>m;
Init();
for(int i=0;i<m;i++)
{
cin>>u>>v>>w;
//g[u][v]=g[v][u]=w;
g[u][v]=w;
}
Traveling(0,0);
cout<<"最短路径: "<<0;
print(0,0);
cout<<endl;
cout<<"最短路径长度:"<<dp[0][0]<<endl;
return 0;
}
例题
思路
由于题中明确说了两个城市间的直接可达路径(即不经过其它城市结点)不一定是最短路径,所以需要借助邻接矩阵首先求出任意两个城市间的最短距离(因为这里的点可以多次遍历,并没有次数限制,所以才能用floyd的,如果有次数限制x的话,就不能用floyd预处理,而应该用x进制的状态压缩了)。这一步骤使用Floyd最短路径算法即可。然后,在此基础上来求出遍历各个城市后回到出发点的最短路径的距离,即求解TSP问题。
//求走过所有点并回到原点的最短路,可以走一个点多次.
//因为可以走一个点多次,所以,可以先求出每两个点之间的最短路,然后用经典的旅行商问题的状态压缩DP做法。
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int N=12,M=1<<11,INF=0x3f3f3f3f;
int n;
int g[N][N];
int dp[M][N];
void Init()
{
memset(dp,-1,sizeof(dp));
memset(g,0x3f,sizeof(g));
}
void floyd()
{
for(int k=0;k<n;k++)
for(int i=0;i<n;i++)
for(int j=0;j<n;j++)
g[i][j]=min(g[i][j],g[i][k]+g[k][j]);
}
int Tsp(int S,int u)//计算dp[S][u],记忆化递归
{
if(dp[S][u]>=0)
return dp[S][u];
if(S==(1<<n)-1&&u==0)//递归结束条件
return dp[S][u]=0;
int ans=INF;
for(int v=0;v<n;v++)
if(!(S>>v&1)&&g[u][v]!=INF)
ans=min(ans,Tsp(S|1<<v,v)+g[u][v]);
return dp[S][u]=ans;
}
int main()
{
while(~scanf("%d",&n),n)
{
n++;//源点0加上
Init();
for(int i=0;i<n;i++)
for(int j=0;j<n;j++)
scanf("%d",&g[i][j]);
floyd();
printf("%d\n",Tsp(0,0));
}
return 0;
}
递推
//求走过所有点并回到原点的最短路,可以走一个点多次.
//因为可以走一个点多次,所以,可以先求出每两个点之间的最短路,然后用经典的旅行商问题的状态压缩DP做法。
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int N=12,M=1<<11,INF=0x3f3f3f3f;
int n;
int g[N][N];
int dp[M][N];
void Init()
{
memset(dp,0x3f,sizeof(dp));//递推时初始化为INF,记忆化递归初始化为-1
memset(g,0x3f,sizeof(g));
}
void floyd()
{
for(int k=0;k<n;k++)
for(int i=0;i<n;i++)
for(int j=0;j<n;j++)
g[i][j]=min(g[i][j],g[i][k]+g[k][j]);
}
void Tsp()//计算dp[S][u]
{
dp[(1<<n)-1][0]=0;//注意:1<<n一定要加括号
for(int S=(1<<n)-2;S>=0;S--)
for(int u=0;u<n;u++)
for(int v=0;v<n;v++)
{
if((u!=0&&!(S>>u&1))||g[u][v]==INF) continue;//可以加约束条件,不加状态多
if(!(S>>v&1))
dp[S][u]=min(dp[S][u],dp[S|1<<v][v]+g[u][v]);
}
}
int main()
{
while(~scanf("%d",&n),n)
{
n++;//加上源点
Init();
for(int i=0;i<n;i++)
for(int j=0;j<n;j++)
scanf("%d",&g[i][j]);
floyd();
Tsp();
printf("%d\n",dp[0][0]);
}
return 0;
}
#include<iostream>
#include<cstring>
#include<cstdio>
using namespace std;
const int N=10,M=35,INF=0x3f3f3f3f;
int n,m,p,a,b;
int t[N];
int g[M][M];
double dp[1<<8][M];//d[S][u],所用车票状态是S,从起点走到点u所需的最短时间
int main()
{
while(cin>>n>>m>>p>>a>>b && n)
{
for(int i=0;i<n;i++)
cin>>t[i];
memset(g,0x3f,sizeof g);
while(p--)
{
int a,b,c;
cin>>a>>b>>c;
g[a][b]=g[b][a]=c;
}
//memset(dp,0x3f,sizeof(dp));//double不可以memset
for(int i=0;i<1<<n;i++)
fill(dp[i]+1,dp[i]+m+1,INF);
// for(int i=0;i<1<<n;i++)
// for(int j=1;j<=m;j++)
// dp[i][j]=INF;
dp[(1<<n)-1][a]=0;
double ans=INF;
for(int S=(1<<n)-1;S>=0;S--)//状态
{
for(int u=1;u<=m;u++)//城市
for(int i=0;i<n;i++)//车票
if(S>>i & 1)
for(int v=1;v<=m;v++)//城市
if(g[u][v] != INF)
dp[S-(1<<i)][v]=min(dp[S-(1<<i)][v],dp[S][u]+g[u][v]/(double)t[i]);
ans=min(ans,dp[S][b]);
}
if(ans == INF)
puts("Impossible");
else
printf("%.3f\n",ans);
}
return 0;
}
hdu3001
题意:
ACMer 想要游玩n个城市,告诉我们每个城市间的旅行费用,并且要求每个城市最多走两遍!问最小花费是多少
本题n=10,数据很小,但是由于每个城市可以走两遍,可能的路线就变成了(2n)!,所以不能暴力
用状压dp,时间复杂度$O(3^{n}n^{2})$



#include<iostream>
#include<cmath>
#include<cstring>
#include<cstdio>
using namespace std;
const int N=15,M=60000,INF=0x3f3f3f3f;
int n,m;
int bit[12]={0,1,3,9,27,81,243,729,2187,6561,19683,59049};//三进制每位为1时对应十进制,如第3位是1,(100)3=9
int tri[M][N];//dp[S][j]状态S的第j位是多少
int dp[M][N];
int g[N][N];
int main()
{
//cout<<pow(3,10)<<endl;
for(int i=0;i<59050;i++)//预处理所有合法状态
{
int t=i;
for(int j=1;j<=10;j++)
{
tri[i][j]=t%3;//预处理当前状态S下每个顶点的访问次数
t/=3;
if(!t)
break;
}
}
while(~scanf("%d%d",&n,&m))
{
int ans=INF;
memset(g,0x3f,sizeof g);
memset(dp,0x3f,sizeof dp);
while(m--)
{
int a,b,c;
cin>>a>>b>>c;
g[a][b]=g[b][a]=min(g[a][b],c);
}
for(int i=1;i<=n;i++)
dp[bit[i]][i]=0;//每个顶点都可以作为起点,初始化状态为tri[i]时,从i出发最小费用为0
for(int S=0;S<bit[n+1];S++)
{
bool visit_all=true;//标记所有的城市都遍历1次以上
for(int u=1;u<=n;u++)
{
if(tri[S][u] == 0)//u点没被访问
{
visit_all=false;//当前状态不能访问所有顶点至少一次
continue;
}
for(int v=1;v<=n;v++)
{
if(tri[S][v] == 0)//v点未访问
continue;
if(g[u][v] != INF)
dp[S][u]=min(dp[S][u],dp[S-bit[u]][v]+g[u][v]);//u从S中减去
}
}
if(visit_all)//所有的城市都遍历1次以上
for(int u=1;u<=n;u++)
ans=min(ans,dp[S][u]);
}
if(ans == INF)
puts("-1");
else
cout<<ans<<endl;
}
return 0;
}
hdu4628
有一个长度不超过 16 的字符串。
每次你可以从中删除一个子序列,但是要求这个子序列是回文的。
问最少删除几次可以把这个字符串删光。
样例:
2
aa (1次)
abb (2次)
每次可以选择一个子序列,而子序列是可以用二进制来表示的。
用一个 n 位的二进制数 s 来表示,如果第 i 位是 1,则表示第 i 个数在这个子序列中。
由此衍生出:用 f[s] 来表示把 s 这个子序列删完的最小步数。
答案自然就是 f[(1 << n) - 1]
一个显然的想法,可以把 s 分成两个不相交的集合 x 和 y, 即 x ∩ y = ∅,x ∪ y = s
f[s] = min(f[s], f[s-x] + 1) (x 是回文子串)
如何判断x是s的子集?
x|s == s
直接枚举 x 和 y 的时间复杂度是 O($2^n$),对于每个状态都有枚举2^n,总时间复杂度是O($4^n$),无法承受。
注意到 x 和 y 都是 s 的子集。
所有集合的子集个数之和的级别是 O(3^n)
就是说一个集合,有n个元素,2^n个子集,把这2^n个子集的所有子集数相加就是3^n
证明可以对每个集合考虑贡献,二项式定理
空集的子集只有一个——它本身.即C(n,0)×2^0个.有一个元素的子集有C(n,1)=n个,它们分别有2^1=2个子集.共C(n,1)×2^1个.有两个元素的子集有C(n,2)个,它们分别有2^2=4个子集.共C(n,2)×2^2个…
我们只要枚举 s 的子集 x,那么 y 自然就是 s - x
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int N=20,M=1<<16;
char s[N];
int f[M];
bool st[M];
int n;
bool check(int x)
{
char str[20];
int tot=0;
for(int i=0;i<n;i++)
if(x>>i & 1) str[tot++]=s[i];
for(int i=0;i<tot/2;i++)
if(str[i] != str[tot-1-i])
return 0;
return 1;
}
void init()
{
memset(st,0,sizeof st);
for(int i=0;i<1<<n;i++)
if(check(i))
st[i]=true;
}
int main()
{
int T;
cin>>T;
while(T--)
{
scanf("%s",s);
n=strlen(s);
init();
memset(f,0x3f,sizeof f);
f[0]=0;
for(int i=0;i<1<<n;i++)
for(int j=i;j;j=(j-1)&i)
if(st[j]) f[i]=min(f[i],f[i-j]+1);
printf("%d\n",f[(1<<n)-1]);
}
return 0;
}
hdu6149
给定一张 N 个点 M 条边的无向图,其中有 K 个点被标记为高点,剩下的 (N-K) 个点是低点。
图中的山谷定义为三元组 [HTML_REMOVED],满足X和Y之间有边,Y与 Z之间也有边,同时X和Z是高点,Y是低点。
问这个图中最多有几个山谷(一个点只能出现在一个山谷中)N ≤ 30, K ≤ min(N,15)
高点最多只有 15 个。
可以考虑用状态压缩,s 表示高点的使用状态。
低点排成一个长度为 n-k 的序列。
f[i][s] 表示前 i 个低点,使用过的高点的状态为 s 的情况下,组成的山谷的最大可能值。
转移 f[i][s] 的时候,取出第 i+1 个低点。
枚举不在 s 中的两个高点 p 和 q.
检查 p 和 q 和第 i+1 个低点能否配对。
如果可以,那么就可以用 f[i][s] + 1 去更新
f[i + 1][s | (1 << p) | (1 << q)]
答案就是 max{ f[n-k][i] | 0 ≤ i < $2^k$ }
#include<iostream>
#include<cstring>
#include<cstdio>
#include<algorithm>
#include<vector>
using namespace std;
typedef pair<int,int> PII;
const int N=35,M=1<<15;
int f[N][M];
int g[N][N];
int n,m,k;
int high[N],low[N];
bool st[N];
vector<PII> trans[N];
int tot;
void init()
{
for(int i=1;i<=n;i++)
if(!st[i])
low[++tot]=i;
for(int i=1;i<=tot;i++)
{
trans[i].clear();
for(int p=0;p<k;p++)
if(g[low[i]][high[p]])
for(int q=p+1;q<k;q++)
if(g[low[i]][high[q]])
trans[i].push_back(make_pair(p,q));
}
}
int main()
{
int T;
cin>>T;
while(T--)
{
memset(g,0,sizeof g);
memset(st,0,sizeof st);
memset(f,0,sizeof f);
tot=0;
scanf("%d%d%d",&n,&m,&k);
for(int i=0;i<m;i++)
{
int x,y;
scanf("%d%d",&x,&y);
g[x][y]=g[y][x]=1;
}
for(int i=0;i<k;i++)
{
scanf("%d",&high[i]);
st[high[i]]=true;
}
init();
for(int i=1;i<=tot;i++)
{
for(int s=0;s<1<<k;s++)
f[i][s]=f[i-1][s];//不选第i个点
for(int s=0;s<1<<k;s++)
{
for(int j=0;j<trans[i].size();j++)
{
int x=trans[i][j].first;
int y=trans[i][j].second;
if(s>>x & 1) continue;
if(s>>y & 1) continue;
f[i][s|(1<<x)|(1<<y)]=max(f[i][s|(1<<x)|(1<<y)],f[i-1][s]+1);//选第i个点
}
}
}
int ans=0;
for(int i=0;i<1<<k;i++)
ans=max(ans,f[tot][i]);
printf("%d\n",ans);
}
return 0;
}
acwing524
数据范围非常小,可以考虑状态压缩DP。 设 f[s] 表示清除掉 s 集合中的猪花费的最小步数。
思考转移。
在已有的 s 集合基础上,再选择一条抛物线使得它经过 t集合的点。
那么就可以用 f[s] + 1 去更新 f[s | t]
三点确定一条抛物线。
而三点之中必须有一个原点,因此只要两个点就能确定一条抛物线。
因此我们可以枚举 s 集合以外的任意两个点,算出经过这两个点的抛物线,枚举所有的点看是否落在抛物线上,得到抛
物线经过的点集 t。
f[s | t] = min(f[s | t], f[s] + 1);
经过点 i 和 j 的抛物线经过的点集 t[i][j] 可以预处理。时间复杂度 O($n^3$)
之后 DP 枚举每个集合,对每个集合都要枚举两个点。
时间复杂度 O($n2^n$)
预处理:
$ax[i]^2 + bx[i] = y[i]$
$ax[j]^2 + bx[j] = y[j]$
解二元一次方程组,得到 a 和 b。
如果 a >= 0,不符合题意,t[i][j] = 0
否则对每个点判断一下是否落在这条抛物线上,如果第 k 个点落在抛物线上,
t[i][j] |= (1 << (k - 1));
#include<iostream>
#include<cstring>
#include<cstdio>
#include<algorithm>
#include<cmath>
using namespace std;
const int N=20,M=1<<18;
const double eps=1e-8;
double x[N],y[N];
int path[N][N];
int f[M];
int n,m;
int cmp(double a,double b)
{
if(fabs(a-b) < eps) return 0;
else return a<b? -1 : 1;
}
void init()
{
for(int i=0;i<n;i++)
{
path[i][i] |= 1<<i;
for(int j=i+1;j<n;j++)
{
if(!cmp(x[i],x[j])) continue;
double a=(y[i]/x[i]-y[j]/x[j])/(x[i]-x[j]);
if(cmp(a,0) >= 0) continue;
double b=y[i]/x[i]-a*x[i];
for(int k=0;k<n;k++)
if(!cmp(a*x[k]*x[k]+b*x[k],y[k])) path[i][j]|=1<<k;
}
}
}
int main()
{
int T;
cin>>T;
while(T--)
{
scanf("%d%d",&n,&m);
for(int i=0;i<n;i++)
scanf("%lf%lf",&x[i],&y[i]);
memset(path,0,sizeof path);
init();
memset(f,0x3f,sizeof f);
f[0]=0;
for(int s=0;s<1<<n;s++)
for(int i=0;i<n;i++)
if(!(s>>i & 1))
{
for(int j=i;j<n;j++)//记得处理只射一只猪的情况(i == j)
{
if(!(s>>j & 1))
f[s|path[i][j]] = min(f[s|path[i][j]],f[s]+1);
}
break;
//对于我们枚举的每一个状态i,我们找到它正数第一只没射掉的猪进行转移后break。
//因为如果我们转移了第一只后面的没射的猪,到时候还要回头来将第一只猪射掉。
//所以后面的没射的猪的转移其实是多余的,射完第一只猪后按顺序接着往后射就可以了。
}
printf("%d\n",f[(1<<n)-1]);
}
return 0;
}
acwing529
简化版题目:
给定一个 n 个点 m 条边的图,请你求出一个有根树,满足每个点的深度和它到父节点的边权乘积之和最小。
n ≤ 12,m ≤ 1000
考虑到点数只有12个,可以考虑状态压缩 DP。 用 s 表示当前加入的点集。
为了方便转移,我们不记录根是谁,而是直接去考虑深度。
也就是用 f[i][s] 表示当前的点集是 s,最深的点为 i。
然后我们去枚举 s 的补集的子集 t,把 t 都作为第 i+1 层加入 s。
我们不用去考虑 t 里的点在这颗树中是否真的是第 i+1层
因为如果不是的话只可能小于i+1层,答案会更小。
那么一定存在一种转移顺序,考虑到这种更优的情况,也就是先把这个点加入 s 集合。
例如,如果第j层中用到的某条边(a, b)应该在比j小的层,假设a是S中的点,b是第j层的点,则在枚举S + {b}时会得到更小的花费。
具体的操作是:
对于 s,枚举 t(s 的补集的子集),检查 t 里的点是否都和 s 里的点有连边,处理出每个点到 s 里的点的最短边。
设这些最短边边权之和为 v。
那么 f[i][s | t] = min(f[i][s | t], f[i - 1][s] + (i - 1) * v)
时间复杂度分析:
s 一共有 $2^n$ 个,s 的补集的子集一共有 $3^n$ 个。
处理 t 里的每个点到 s 里的点的最短边,预处理时间复杂度 O($n^2$)
验证 t 是否可行,时间复杂度 O(n)。
转移时对每个深度都要更新一次,时间复杂度O(n)
总时间复杂度就是 O($n^22^n + n3^n$),即 O($n3^n$)
#include<iostream>
#include<cstring>
#include<cstdio>
#include<algorithm>
#include<bitset>
using namespace std;
const int N=15,M=1<<12,INF=0x3f3f3f3f;
int f[M][N];
int g[N][N];
int dist[M][N];
int n,m;
void init()
{
memset(dist,0x3f,sizeof dist);
for(int s=0;s<1<<n;s++)//集合s
for(int i=0;i<n;i++)
if(!(s>>i & 1))//枚举不在集合s中的点i
for(int j=0;j<n;j++)
if(s>>j & 1)//预处理出i到集合s的最短距离
dist[s][i]=min(dist[s][i],g[i][j]);
}
int main()
{
scanf("%d%d",&n,&m);
memset(g,0x3f,sizeof g);
while(m--)
{
int a,b,c;
scanf("%d%d%d",&a,&b,&c);
a--,b--;
g[a][b]=g[b][a]=min(g[a][b],c);
}
init();
memset(f,0x3f,sizeof f);
for(int i=0;i<n;i++) f[1<<i][1]=0;
for(int s=0;s<1<<n;s++)//集合s
{
int c=(1<<n)-1-s;
for(int t=c;t;t=(t-1)&c)//集合s的补集t
{
int sum=0;
for(int i=0;i<n;i++)
if(t>>i & 1)
{
sum+=dist[s][i];
if(sum >= INF) break;
}
if(sum < INF)
for(int i=1;i<=n;i++)
f[s|t][i]=min(f[s|t][i],f[s][i-1]+(i-1)*sum);
}
}
int ans=INF;
for(int i=1;i<=n;i++)
ans=min(ans,f[(1<<n)-1][i]);
printf("%d\n",ans);
return 0;
}






](https://cdn.acwing.com/media/article/image/2020/02/14/9969_59ec7a564f-26888.png)

总结得很棒!
支持