1) 区间dp模型
emmm…就是状态是一种区间的形式(类似于[L,R]之类的),同时一段大区间可以转化一些小区间,并且大区间和小区间之间是相互独立的,在处理完小区间之后可以回溯处理大区间。
可以用递推和记忆化搜索来解决
在用递推求解时,通常是先枚举区间是从小到大。
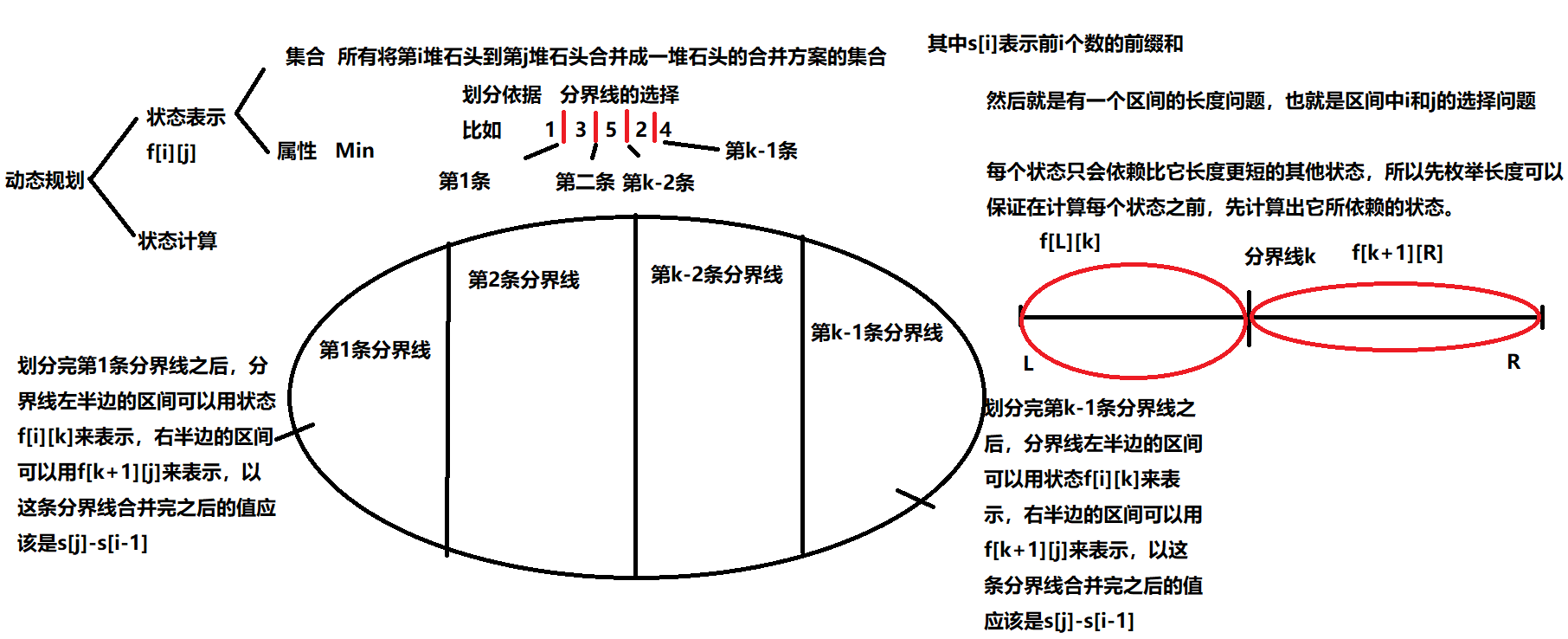
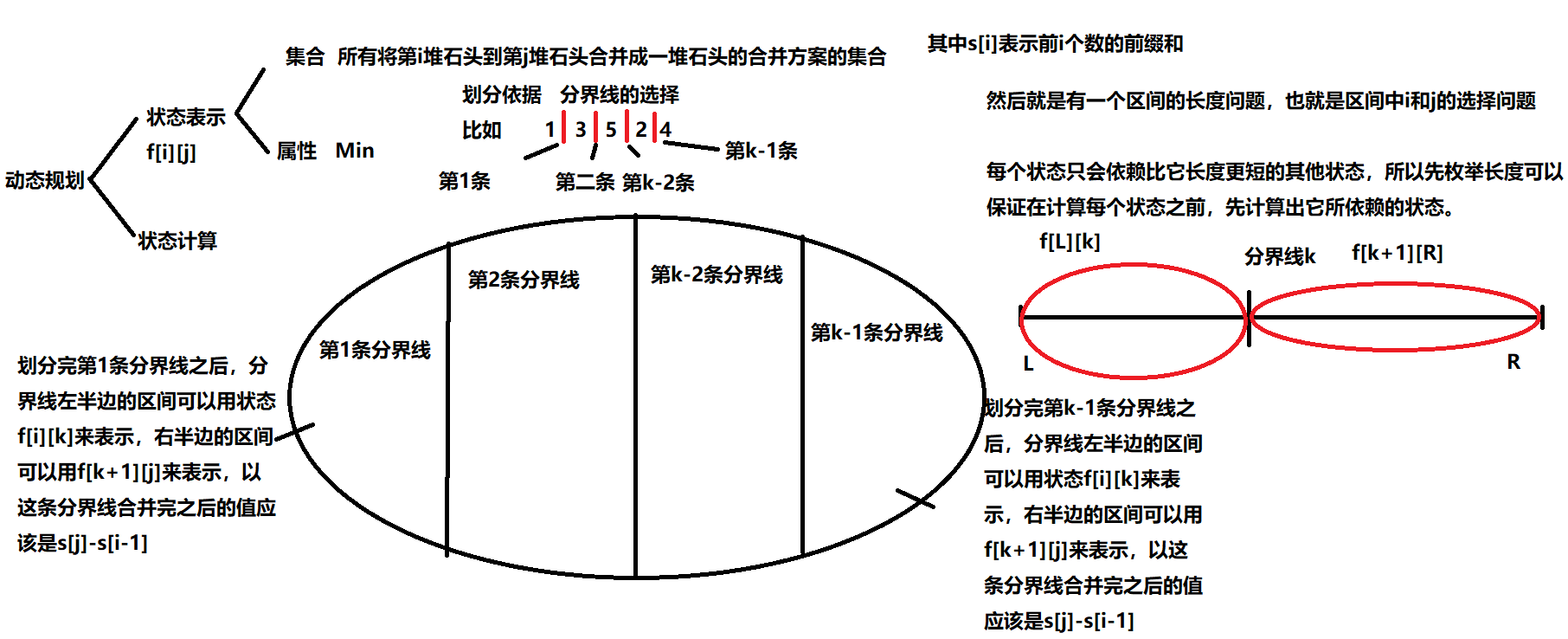
emmm…将n堆石头合并成为一堆石头,通过题目可以发现通过划分不同的分界线合并方式值不一样。因为一共有n堆石头,所以最后一共有n-1条有效的划分线

emmm…然后就是y总的dp分析法
#include<iostream>
#include<algorithm>
using namespace std;
const int N = 310;
int f[N][N], n, a[N], s[N], g[N][N];
void print(int l, int r)
{
if(l >= r) return ;
int k = g[l][r];
print(l, k);
print(k + 1, r);
printf("合并第 %d 到 %d 这一堆和合并第 %d 到 %d 这一堆\n", l, k, k + 1, r);
}
int main()
{
cin >> n;
for(int i = 1; i <= n; i ++) scanf("%d", &a[i]);
for(int i = 1; i <= n; i ++) s[i] += s[i - 1] + a[i];
for(int len = 2; len <= n; len ++)
for(int i = 1; i + len - 1 <= n; i ++){
int l = i, r = i + len - 1;
f[l][r] = 1e9;
for(int k = l; k < r; k ++)
if(f[l][k] + f[k + 1][r] + s[r] - s[l - 1] < f[l][r]){
f[l][r] = min(f[l][r], f[l][k] + f[k + 1][r] + s[r] - s[l - 1]);
g[l][r] = k;
}
}
// print(1, n);
cout << f[1][n] << endl;
return 0;
}
emmm…需要将n堆石头合并成一堆石头一共需要n-1条边,但是这个题目一共有n条边所以我们需要枚举每次去掉其中的一条边然后将这个环拉成一条链,然后对这条链做一次上题所述的dp,这样的时间复杂度(n^4)太高了。
所以这个题目可以将n堆石子补成2*n堆石子
比如有n堆石子 4 5 9 4 可以将其补成 4 5 9 4 4 5 9 4
这样我们只需要对2*n堆石子做一次区间dp,
然后枚举长度为n的区间长度,然后对其中dp值找最大值和最小值(相当于我们枚举了缺口的位置)
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
using namespace std;
const int N = 210, inf = 0x3f3f3f3f;
int a[2 * N], s[2 * N], f[N][N], n, g[N][N];
int main()
{
cin >> n;
for(int i = 1; i <= n; i ++){
cin >> a[i];
a[i + n] = a[i];
}
for(int i = 1; i <= n * 2; i ++) s[i] += s[i - 1] + a[i];
memset(f, 0x3f, sizeof f);
memset(g, -0x3f, sizeof g);
for(int len = 1; len <= n; len ++)
for(int l = 1; l + len - 1 <= n * 2; l ++){
int r = l + len - 1;
if(len == 1) f[l][r] = g[l][r] = 0;
else{
for(int k = l; k < r; k ++){
f[l][r] = min(f[l][k] + f[k + 1][r] + s[r] - s[l - 1], f[l][r]);
g[l][r] = max(g[l][k] + g[k + 1][r] + s[r] - s[l - 1], g[l][r]);
}
}
}
int res1 = inf, res2 = -inf;
for(int i = 1; i <= n; i ++){
res1 = min(res1, f[i][i + n - 1]);
res2 = max(res2, g[i][i + n - 1]);
}
cout << res1 << endl << res2 << endl;
return 0;
}
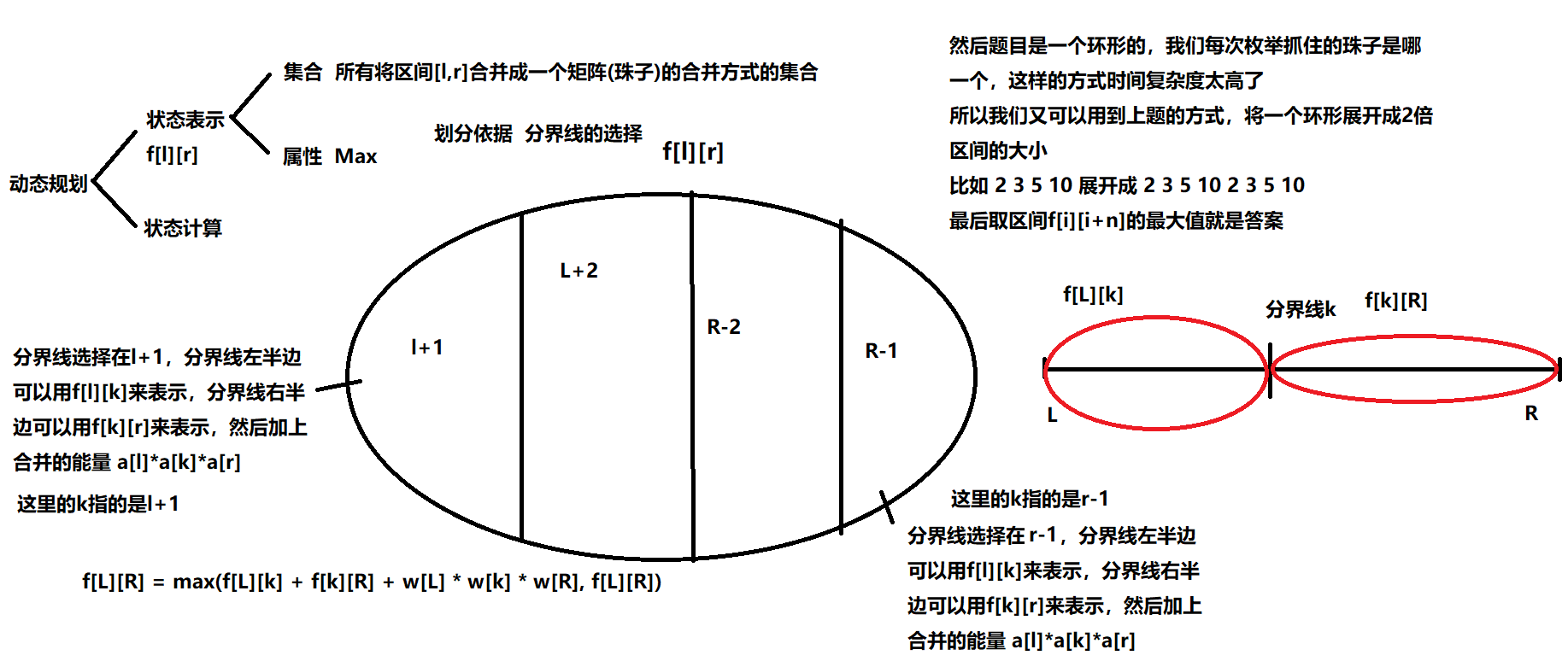
emmm…首先这是一个环形的题目,所以我们需要先将其展开成线性的,然后因为这个合并方式和矩阵乘法非常相似,最终一定会只剩下一个数(也就是一个a*a的矩阵)

emmm…然后就是y总的dp分析法了
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 210, inf = 0x3f3f3f3f;
int a[N], f[N][N], n;
int main()
{
cin >> n;
for(int i = 1; i <= n; i ++){
cin >> a[i];
a[i + n] = a[i];
}
for(int len = 3; len <= n + 1; len ++)
for(int l = 1; l + len - 1 <= n * 2; l ++){
int r = len + l - 1;
for(int k = l + 1; k < r; k ++)
f[l][r] = max(f[l][r], f[l][k] + f[k][r] + a[l] * a[k] * a[r]);
}
int res = 0;
for(int i = 1; i <= n; i ++) res = max(res, f[i][i + n]);
cout << res << endl;
return 0;
}
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
typedef long long ll;
const int N = 55;
int w[N], n;
ll f[N][N][N];
void mul(ll a[], ll b)
{
static ll c[N];
memset(c, 0, sizeof c);
ll t = 0;
for(int i = 0; i < N; i ++){
t += a[i] * b;
c[i] = t % 10;
t /= 10;
}
memcpy(a, c, sizeof c);
}
void add(ll a[], ll b[])
{
static ll c[N];
memset(c, 0, sizeof c);
ll t = 0;
for(int i = 0; i < N; i ++){
t += a[i] + b[i];
c[i] = t % 10;
t /= 10;
}
memcpy(a, c, sizeof c);
}
int cmp(ll a[], ll b[])
{
for(int i = N - 1; i >= 0; i --)
if(a[i] > b[i]) return 1;
else if(a[i] < b[i]) return -1;
return 0;
}
void print(ll a[])
{
int k = N - 1;
while(k && !a[k]) k --;
while(k >= 0) cout << a[k -- ];
cout << endl;
}
int main()
{
cin >> n;
for(int i = 1; i <= n; i ++) cin >> w[i];
ll temp[N];
for(int len = 3; len <= n; len ++)
for(int l = 1; l + len - 1 <= n; l ++){
int r = l + len - 1;
f[l][r][N - 1] = 1;
for(int k = l + 1; k < r; k ++){
memset(temp, 0, sizeof temp);
temp[0] = w[l];
mul(temp, w[k]);
mul(temp, w[r]);
add(temp, f[l][k]);
add(temp, f[k][r]);
if(cmp(temp, f[l][r]) < 0)
memcpy(f[l][r], temp, sizeof temp);
}
}
print(f[1][n]);
return 0;
}
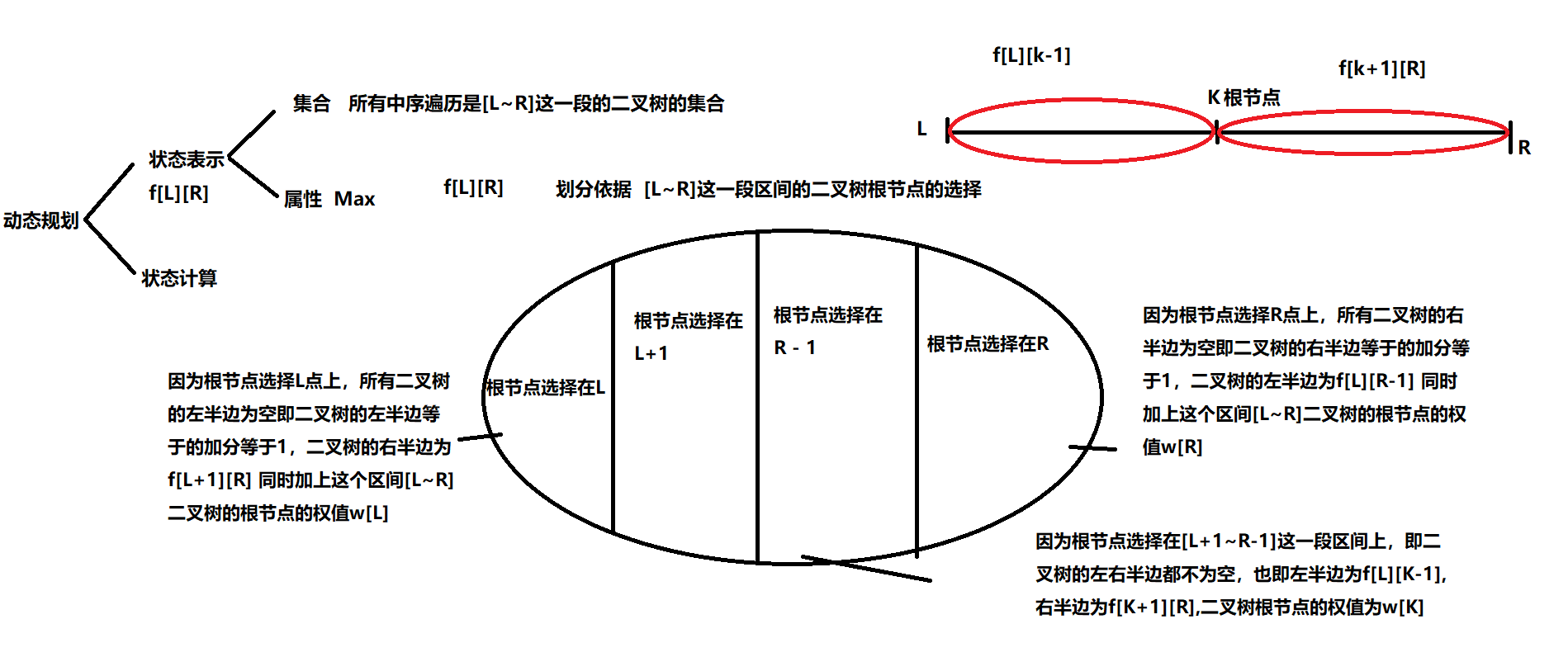
#include<iostream>
#include<cstring>
using namespace std;
const int N = 35;
int f[N][N], g[N][N], n, w[N];
void dfs(int l, int r)
{
if(l > r) return ;
int k = g[l][r];
cout << k << " ";
dfs(l, k - 1);// 先递归遍历左子树
dfs(k + 1, r);
}
int main()
{
cin >> n;
for(int i = 1; i <= n; i ++) cin >> w[i];
for(int len = 1; len <= n; len ++ )
for(int l = 1; l + len - 1 <= n; l ++ ){
int r = l + len - 1;
if(len == 1){
f[l][r] = w[l];
g[l][r] = l;
}else{
for(int k = l; k <= r; k ++ ){// 枚举根节点的划分
int le, ri;
if(k == l) le = 1;
else le = f[l][k - 1];
if(k == r) ri = 1;
else ri = f[k + 1][r];
if(ri * le + w[k] > f[l][r]){
f[l][r] = le * ri + w[k];
g[l][r] = k;// 记录当前区间选择了那个根节点
}
}
}
}
cout << f[1][n] << endl;
dfs(1, n);
return 0;
}
emmm…下次来补
2)树形dp
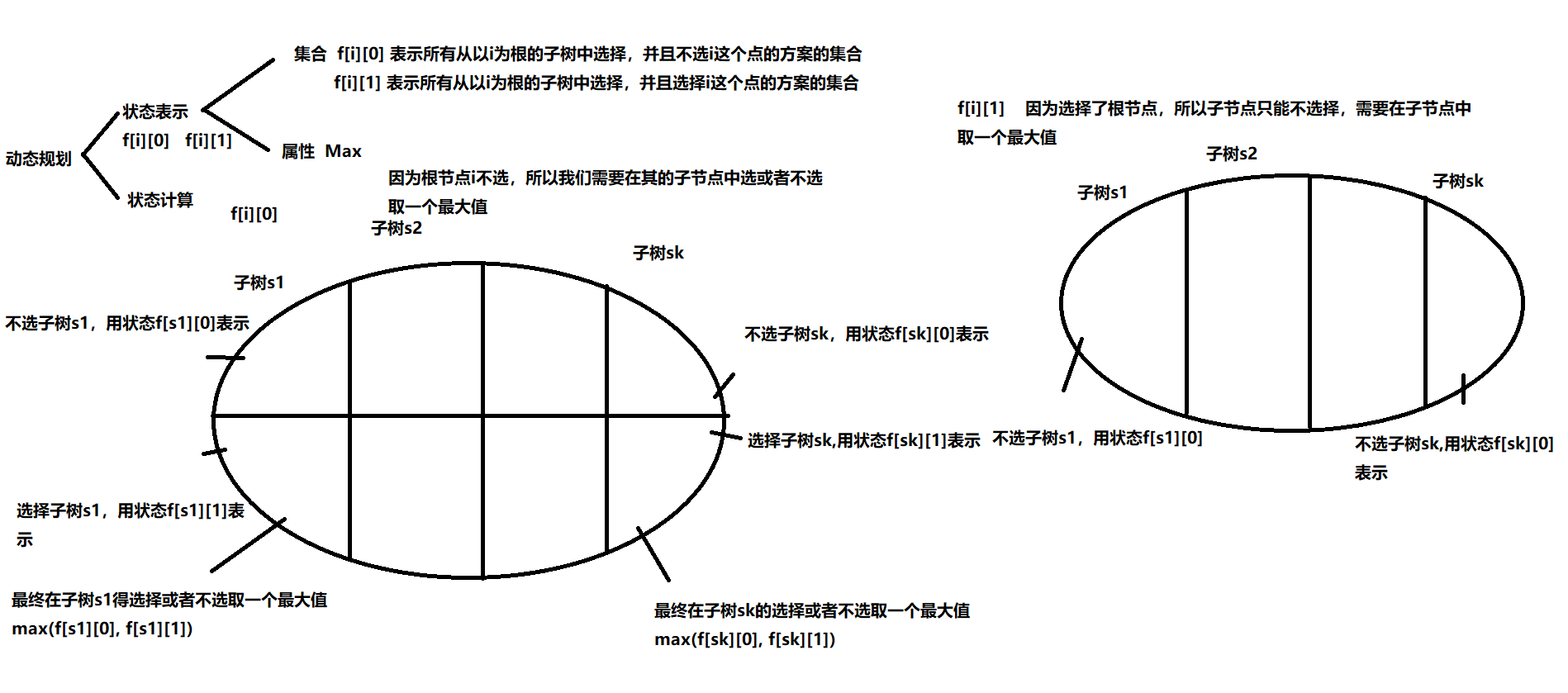
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 6010, M = N * 2;
int h[N], e[M], ne[M], idx;
int n, w[N], fa[N], f[N][N];
void add(int a, int b)
{
e[idx] = b, ne[idx] = h[a], h[a] = idx ++;
}
void dfs(int u)
{
f[u][1] = w[u];
for(int i = h[u]; ~i; i = ne[i]){
int j = e[i];
dfs(j);// 一定要先递归子树,算出子树的值
f[u][0] += max(f[j][0], f[j][1]);
f[u][1] += f[j][0];
}
}
int main()
{
cin >> n;
for(int i = 1; i <= n; i ++) cin >> w[i];
memset(h, -1, sizeof h);
for(int i = 1; i < n; i ++){
int a, b;
cin >> a >> b;
add(b, a);
fa[a] = b;
}
int root = 1;
while(fa[root]) root ++;
dfs(root);
cout << max(f[root][0], f[root][1]) << endl;
return 0;
}
emmm…这个题目和没有上司的舞会具有对称性
没有上司的舞会:每条边上最多选择一个点,求最大权值
战略游戏:每条边上最少选择一个点,求最小权值

#include<iostream>
#include<cstring>
#include<cstdio>
#include<algorithm>
using namespace std;
const int N = 1510;
int n, f[N][2];
bool st[N];
int h[N], ne[N], e[N], idx;
void add(int a, int b)
{
e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}
void dfs(int u)
{
f[u][0] = 0, f[u][1] = 1;
for(int i = h[u]; ~i; i = ne[i]){
int j = e[i];
dfs(j);
f[u][0] += f[j][1];
f[u][1] += min(f[j][0], f[j][1]);
}
}
int main()
{
while(cin >> n){
memset(h, -1, sizeof h);
idx = 0;
memset(st, 0, sizeof st);
for(int i = 0; i < n; i ++){
int a, b, cnt;
scanf("%d:(%d)", &a, &cnt);
while(cnt --){
scanf("%d", &b);
add(a, b);
st[b] = 1;
}
}
int root = 0;
while(st[root]) root ++;
dfs(root);
cout << min(f[root][0], f[root][1]) << endl;
}
return 0;
}
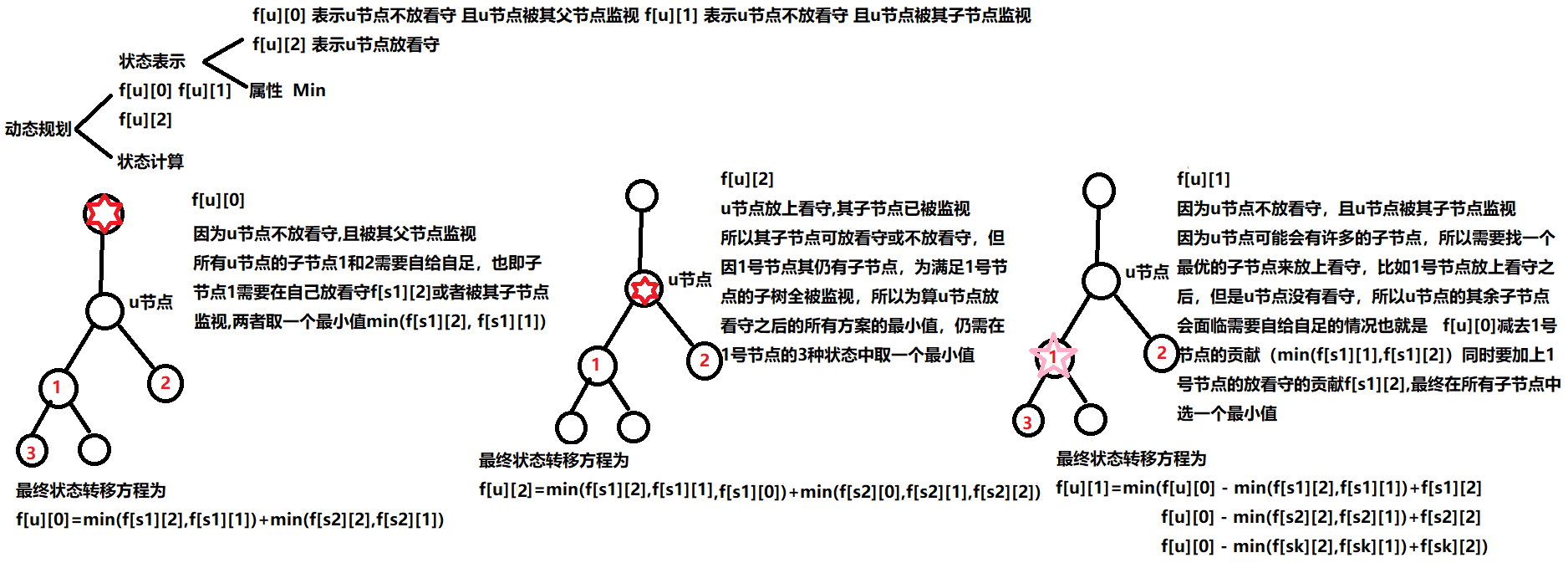
#include<iostream>
#include<algorithm>
#include<cstring>
#include<cstdio>
using namespace std;
const int N = 1510;
int n, f[N][3];
int h[N], ne[N], e[N], w[N], idx;
bool st[N];
void add(int a, int b)
{
e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}
void dfs(int u)
{
f[u][2] = w[u];
for(int i = h[u]; ~i; i = ne[i]){
int j = e[i];
dfs(j);
f[u][0] += min(f[j][1], f[j][2]);
f[u][2] += min(f[j][0], min(f[j][1], f[j][2]));
}
f[u][1] = 1e9;
for(int i = h[u]; ~i; i = ne[i]){
int j = e[i];
f[u][1] = min(f[u][1], f[u][0] - min(f[j][1], f[j][2]) + f[j][2]);
}
}
int main()
{
memset(h, -1, sizeof h);
cin >> n;
for(int i = 1; i <= n; i ++){
int a, b, cnt;
cin >> a >> w[a] >> cnt;
while(cnt -- ){
scanf("%d", &b);
add(a, b);
st[b] = 1;
}
}
int root = 1;
while(st[root]) root ++ ;
dfs(root);
// cout << f[root][1] << endl;
cout << min(f[root][1], f[root][2]) << endl;
return 0;
}

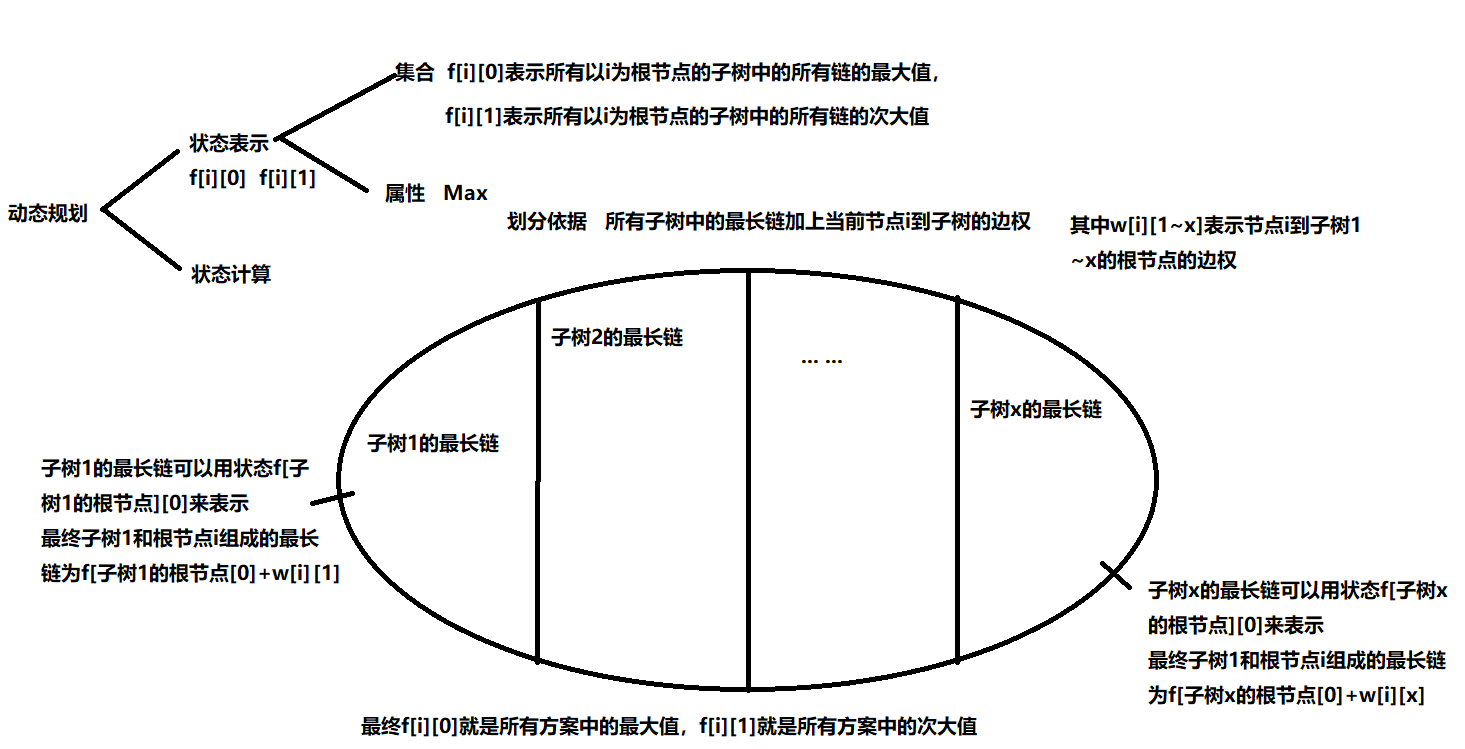
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 1e5 + 10, M = 2e5 + 10;
int h[N], ne[M], e[M], w[M], idx;
int n, ans;
void add(int a, int b, int c)
{
e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++;
}
int dfs(int u, int fa)
{
int d1 = 0, d2 = 0;// d1表示最长链, d2表示次长链
for(int i = h[u]; ~i; i = ne[i]){
int j = e[i];
if(j == fa) continue;
int d = dfs(j, u) + w[i];// d表示当前子树中的最长链
if(d >= d1) d2 = d1, d1 = d;
else if(d > d2) d2 = d;
}
ans = max(ans, d1 + d2);
return d1;
}
int main()
{
memset(h, -1, sizeof h);
cin >> n;
for(int i = 1; i < n; i ++){
int a, b, c;
cin >> a >> b >> c;
add(a, b, c), add(b, a, c);
}
dfs(1, -1);
cout << ans << endl;
return 0;
}

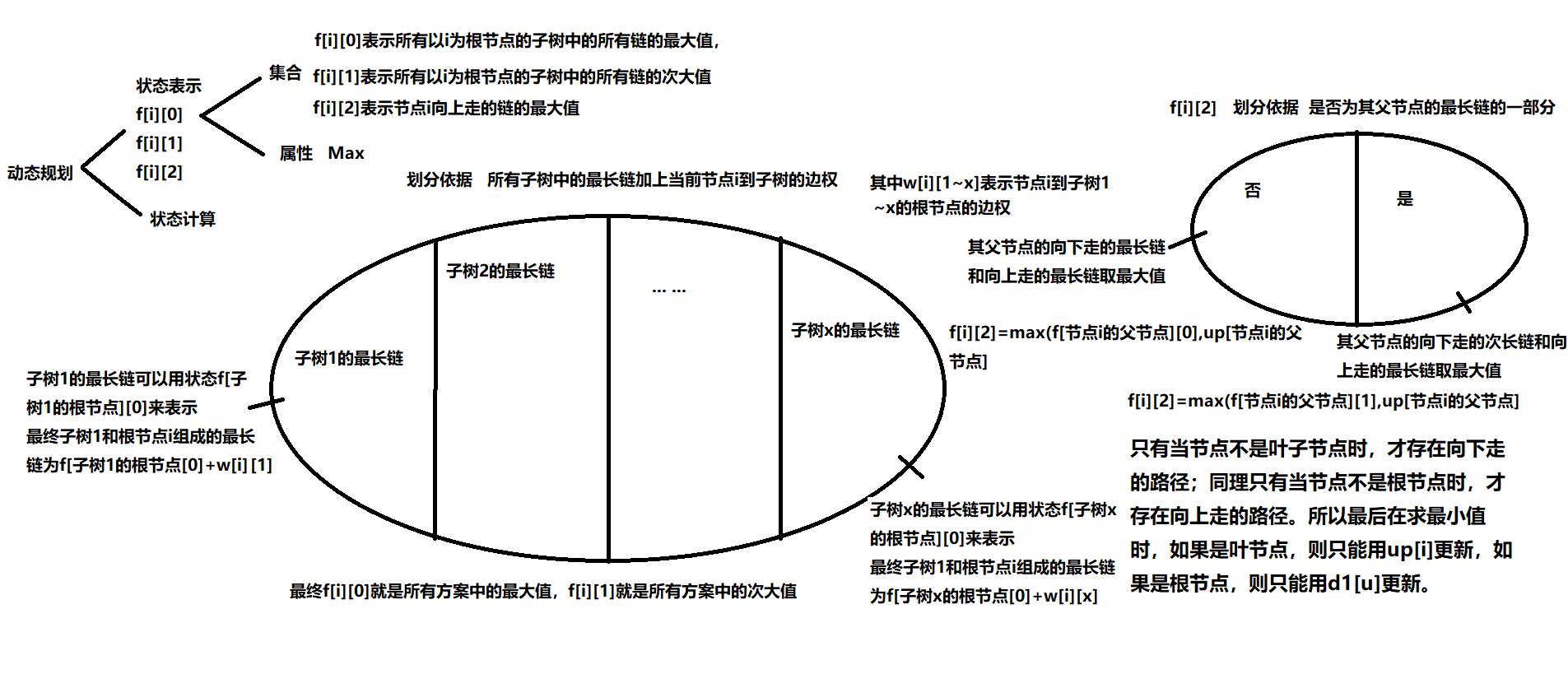
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 1e4 + 10, M = 2e4 + 10, inf = 0x3f3f3f3f;
int n, d1[N], d2[N], up[N], p[N];//p数组记录向下走的最长链的子节点
int h[N], e[M], ne[M], idx, w[M];
bool is_le[N];
void add(int a, int b, int c)
{
e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++;
}
int dfs_d(int u, int fa)
{
d1[u] = -inf, d2[u] = -inf;//d1记录向下走的最长链,d2记录向下走的次长链
for(int i = h[u]; ~i; i = ne[i]){
int j = e[i];
if(j == fa) continue;
int d = dfs_d(j, u) + w[i];
if(d >= d1[u]) d2[u] = d1[u], d1[u] = d, p[u] = j;
else if(d > d2[u]) d2[u] = d;
}
if(d1[u] == -inf){// 不会被更新代表是叶子节点
d1[u] = d2[u] = 0;
is_le[u] = 1;
}
return d1[u];
}
void dfs_u(int u, int fa)
{
for(int i = h[u]; ~i; i = ne[i]){
int j = e[i];
if(j == fa) continue;
if(j == p[u]) up[j] = max(up[u], d2[u]) + w[i];// 如果当前子节点是其父节点的最长链的一部分
else up[j] = max(up[u], d1[u]) + w[i];
dfs_u(j, u);
}
}
int main()
{
memset(h, -1, sizeof h);
cin >> n;
for(int i = 1; i < n; i ++){
int a, b, c;
cin >> a >> b >> c;
add(a, b, c), add(b, a, c);
}
dfs_d(1, -1);
dfs_u(1, -1);
int res = inf;
for(int i = 1; i <= n; i ++)
if(is_le[i]) res = min(res, up[i]);
else res = min(res, max(d1[i], up[i]));
cout << res << endl;
return 0;
}
emmm...可以由每个数的约数之和向其数本身连一条边,这样就能连成一棵树,最终就是在这颗树上求最长链
每个数的约数之和是唯一的,但同一个数可能是多个数的约数之和。因此应该由每个数的约数之和向它本身连边,这样能保证每个点只有一个父节点,从而才可以形成一棵树。边反向之后就不一定是树了。
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 5e4 + 10, M = 1e5 + 10;
int h[N], e[M], ne[M], idx;
int n, sum[N], ans;
void add(int a, int b)
{
e[idx] = b, ne[idx] = h[a], h[a] = idx ++;
}
int dfs(int u)
{
int d1 = 0, d2 = 0;
for(int i = h[u]; ~i; i = ne[i]){
int j = e[i];
int d = dfs(j) + 1;
if(d >= d1) d2 = d1, d1 = d;
else if(d > d2) d2 = d;
}
ans = max(ans, d1 + d2);
return d1;
}
int main()
{
memset(h, -1, sizeof h);
cin >> n;
for(int i = 1; i <= n; i ++)
for(int j = 2; j <= n / i; j ++)
sum[j * i] += i;
for(int i = 1; i <= n; i ++)
if(sum[i] < i)
add(sum[i], i);
for(int i = 1; i <= n; i ++)
dfs(i);
cout << ans << endl;
return 0;
}
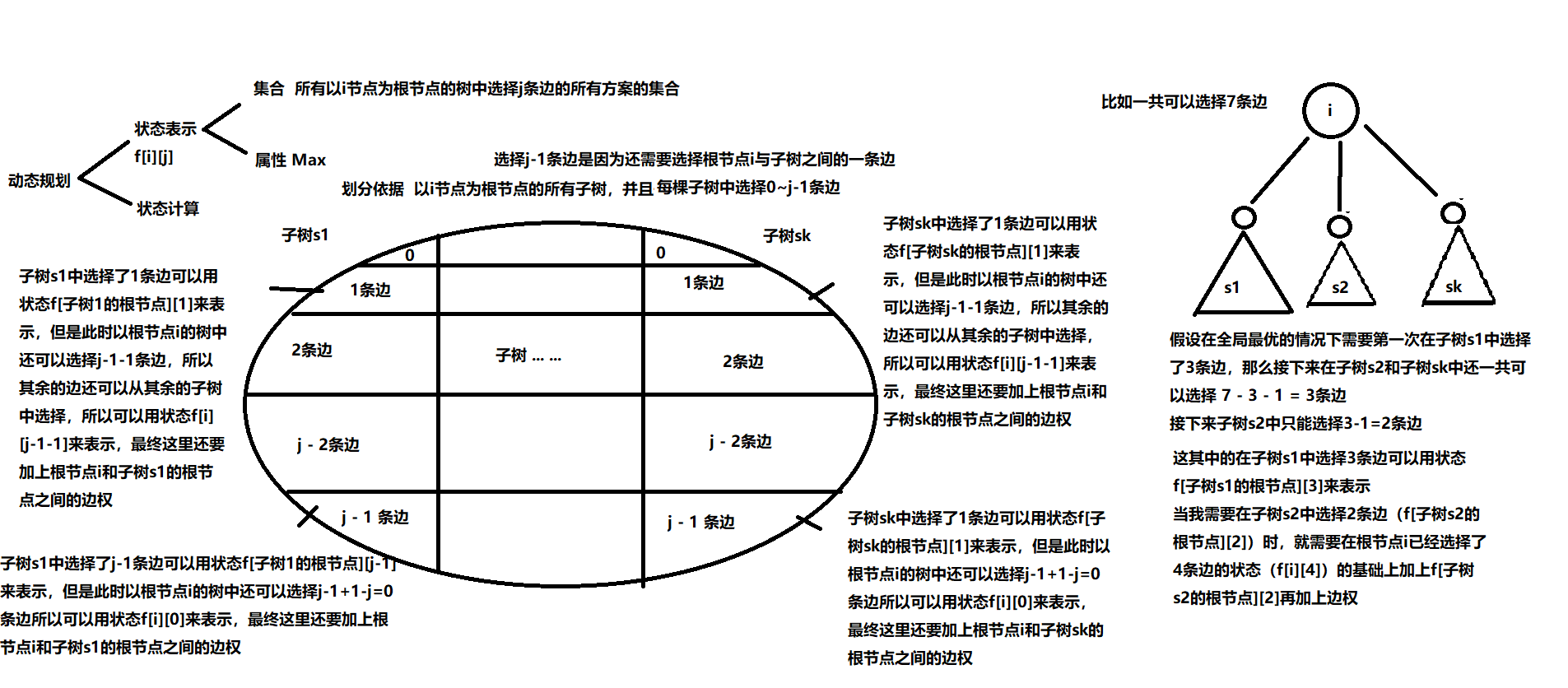
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 110, M = 200 + 10;
int h[N], ne[M], e[M], w[M], idx;
int n, f[N][N], m;
void add(int a, int b, int c)
{
e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++;
}
void dfs(int u, int fa)
{
for(int i = h[u]; ~i; i = ne[i]){
int v = e[i];
if(v == fa) continue;
dfs(v, u);
for(int j = m; j >= 0; j --)// 需要枚举体积,并且因为01背包,需要从大到小
for(int k = 0; k + 1 <= j; k ++)// 枚举子树中的选择
f[u][j] = max(f[u][j], f[u][j - k - 1] + f[v][k] + w[i]);
}
}
int main()
{
memset(h, -1, sizeof h);
cin >> n >> m;
for(int i = 1; i < n; i ++){
int a, b, c;
cin >> a >> b >> c;
add(a, b, c), add(b, a, c);
}
dfs(1, -1);
cout << f[1][m] << endl;
// cout << f[3][2] << endl;
return 0;
}
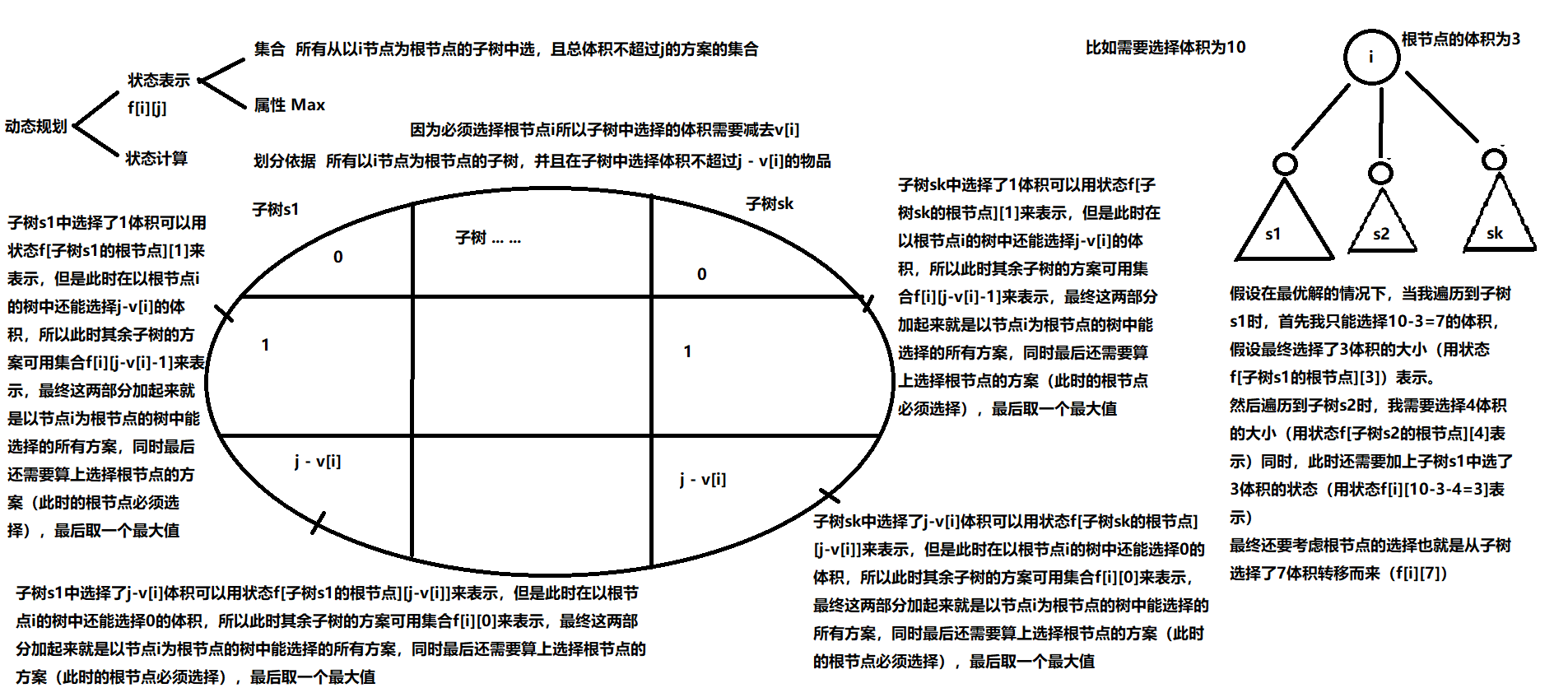
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 110, M = 200 + 10;
int h[N], ne[M], e[M], idx;
int n, f[N][N], root, w[N], m, v[N];
void add(int a, int b)
{
e[idx] = b, ne[idx] = h[a], h[a] = idx ++;
}
void dfs(int u)
{
for(int i = h[u]; ~i; i = ne[i]){
int ver = e[i];
dfs(ver);// 先遍历子节点,先算子状态的值,然后回溯算大状态的值
for(int j = m - v[u]; j >= 0; j --)// 因为必须考虑根节点所以必须从m-根节点的体积开始循环
for(int k = 0; k <= j; k ++)
f[u][j] = max(f[u][j], f[u][j - k] + f[ver][k]);
}
for(int j = m; j >= v[u]; j --) f[u][j] = f[u][j - v[u]] + w[u];// 考虑根节点的情况(此时必须选择)
for(int j = v[u] - 1; j >= 0; j -- ) f[u][j] = 0;
}
int main()
{
memset(h, -1, sizeof h);
cin >> n >> m;
for(int i = 1; i <= n; i ++){
int p;
cin >> v[i] >> w[i] >> p;
if(p == -1) root = i;
else add(p, i);
}
dfs(root);
cout << f[root][m] << endl;
return 0;
}


点赞 收藏 评论 三连~~
妙哉