概率dp
概率DP主要用于求解期望、概率等题目。
转移方程有时候比较灵活。
一般求概率是正推,求期望是逆推。通过题目可以体会到这点。
常规的dp[x]可能表示到了x这一状态有多少,最后答案是dp[n]。而数学期望的dp[x]一般表示到了x这一状态还差多少,最后答案是dp[0]。
一般来说,概率DP找到正确的状态定义后,转移是比较容易想到的。但状态一定是“可数”的,把有范围的整数作为数组下标。事实上,将问题直接作为状态是最好的。如问“n人做XX事的期望次数”,则设计状态为f[i]表示i个人做完事的期望。转移一般是递推,即从上一个状态转移得(填表)或转移向下一个状态(刷表)
有时期望DP需以最终状态为初始状态转移,即逆推。如f[i]表示期望还要走f[i]步到达终点。这种状态的转移是刷表法,形如$f[i]=∑p[i→j]f[j]+w[i→j]f[i]=∑p[i→j]f[j]+w[i→j]$,其中p[]表示转移的概率,w[]表示转移对答案的贡献。一般来说,初始状态确定时可用顺推,终止状态确定时可用逆推。
有些DP方程之间会循环转移。可以高斯消元,或者设每个状态为形如$f[u]=a[u]f[fa]+b[u]f[0]+c[u]$,最后求出所有系数。
预备知识



引例
涂格子1
n个格子,每次随机涂一个,求涂满m个格子的期望次数。
题解

涂格子2
n个格子,每次随机涂一个,求涂m次后期望涂色格子数。
题解

令$k=\frac{n-1}{n}$
$f_n=kf_{n−1}+1$
$f_n+\frac{1}{k−1}=kf_{n−1}+\frac{k}{k-1}$
$f_{n}+\frac{1}{k−1}=k(f_{n-1}+\frac{1}{k−1})$
令$g_n=f_n+\frac{1}{k−1}$
则$g_n=kg_{n−1}$
怎么求$g_n$就不用说了吧,相信大家高中数学一定都学的比我好QAQ
$f_n=g_n−\frac{1}{k−1}$
于是$f_n$也能求出来了
这是我推的结果
$f[n]=n(1-(\frac{n-1}{n})^m)$
易知f[0] = 0,f[1]=1,采用顺推,答案为f[m]。
转移方程为
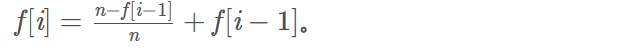
涂格子3

求涂满n个格子的期望次数。
题解
这个和1其实很类似,因为每个格子只能涂一次但概率不同,所以没法把“格子数量”当成一维状态,只能使用状压。
f[S]:状态S到全部格子都被涂的期望次数。
当S=$2^{n}$−1时,f[S]=0。
采用逆推,转移时枚举涂哪个格子即可
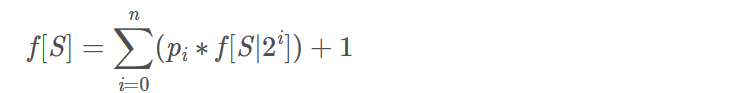
这里i必须是S中为0的位置。
无论从哪里转移而来,此次的次数都要加1。
例题
小孩和礼物
有n个礼物盒和m个小孩,每个盒子里有一个礼物。所有人轮流开盒子,每次打开一个随机盒子,如果里面有礼物就拿走(如果被开过了就没有礼物了)。问所有人拿走礼物的期望数量。
题解
f[i]表示i个人拿走礼物的期望,相当于表示涂i次期望涂色格子数量。同涂格子2。
#include<iostream>//推公式
#include<cmath>
using namespace std;
int main()
{
int n;
int m;
cin>>n>>m;
double res=0;
res=n*(1-pow((n-1)*1.0/n,m));
printf("%.9f\n",res);
return 0;
}
#include<iostream>//递推
#include<cmath>
using namespace std;
const int N=100010;
double dp[N];
int main()
{
int n;
int m;
cin>>n>>m;
for(int i=1;i<=m;i++)
{
dp[i]=(n-dp[i-1])/n+dp[i-1];
}
printf("%.9f\n",dp[m]);
return 0;
}
麻球繁衍
题意:
有K只麻球,每只生存一天就会死亡,每只麻球在死之前有可能生下一些麻球,生i个麻球的概率是pi,问m天后所有的麻球都死亡的概率是多少?
思路
涉及到全概率公式,因为麻球的各种活动都互不影响,所以现在只考虑一只麻球,
我们假设f[i]是i天后所有麻球全部都死亡的概率,那么
$f[i]= p_0 + p_1f[i-1] + p_2f[i-1]^2 + …p_{n-1}f[i - 1]^{(n-1)}$
其中$p_jf(i−1)^j$的含义是在i-1天的麻球生了j个后代(生的概率为$p_j$)。注意这j个后代的死亡时独立的,而每一死亡的概率都是$f(i−1)$(i-1天后死亡),因此根据乘法原理,j个后代i-1天后全部死亡的概率为$f(i−1)^j$。同理,由于一开始共有k只麻球,且各只麻球的死亡是独立的,由乘法原理,最终答案是$f(m)^k$。
f[0]=0,f[1]=$p_0$(要求第一天死绝,则第一天不能生任何麻球),采用顺推
#include<iostream>
#include<cmath>
using namespace std;
const int N=1010;
int n,k,m;
double p[N];
double f[N];
int main()
{
int T;
cin>>T;
for(int kase=1;kase<=T;kase++)
{
cin>>n>>k>>m;
for(int i=0;i<n;i++)
cin>>p[i];
f[0]=0,f[1]=p[0];
for(int i=2;i<=m;i++)
{
f[i]=0;
for(int j=0;j<n;j++)
f[i]+=p[j]*pow(f[i-1],j);
}
printf("Case #%d: %.7f\n",kase,pow(f[m],k));
}
return 0;
}
poj3682
题意:
每天抛一个硬币,硬币正面朝上的几率是p,直到抛出k次正面为止结束,第一天抛硬币需花费1,第二天花费3,然后是5,7,9……以此类推,让我们求出抛硬币的天数的期望和花费的期望。
DP解法


边界:E[k]=0
边界: F[k]=0。
#include<iostream>
using namespace std;
const int N=1010;
double E[N],F[N];
int k;
double p;
int main()
{
while(cin>>k && k)
{
cin>>p;
E[k]=0;
F[k]=0;
for(int i=k-1;i>=0;i--)
{
E[i]=E[i+1]+1.0/p;
F[i]=F[i+1]+(2*E[i]-1)/p;
}
printf("%.3f %.3f\n",E[0],F[0]);
}
return 0;
}
题意
有一个长度为n的01序列,每一段极大的连续1的价值是L^3(长度L)。现在给定n个实数表示该位为1的概率,求期望总价值。
思路
后缀长度是一个很关键的量,设g[i]表示前i个的后缀长度期望。根据全期望公式,依赖于第i-1位为0或1:(以下所有公式最后省略+(1-ai)*0)
$g[i]=ai∗(g[i−1]+1)$
设f[i]表示前i个的价值期望,当第i-1位为1时,f[i]相对于f[i-1]的价值多了$[(g[i-1]+1)^3]$ - $[g[i-1]^3 ]$的代价,即:
$f[i]=f[i-1]\times(1-a_i)+a_i\times(f[i-1]+3∗g[i−1]^2+3g[i−1]+1)$
等等,这没有结束,只有加法和乘法满足期望的线性,不包括乘方。通俗地说,期望的乘方不等于乘方的期望。
设g2[i]表示前i个“后缀长度的平方”的期望,同样的g2[i]相对于g2[i-1]多了$[(g[i-1]+1)^2] - [ g[i-1]^2 ]$,即:
$g2[i]=a_i\times(g2[i−1]+2∗g[i−1]+1)$
边界:g[0]=0,g2[0]=0,f[0]=0;正推
#include<iostream>
#include<cstdio>
using namespace std;
const int N=100010;
double g[N],g2[N],f[N];
int n;
int main()
{
cin>>n;
for(int i=1;i<=n;i++)
{
double x;
cin>>x;
g[i]=(g[i-1]+1)*x;
g2[i]=(g2[i-1]+2*g[i-1]+1)*x;
f[i]=f[i-1]+(3*g2[i-1]+3*g[i-1]+1)*x;
}
printf("%.1f",f[n]);
return 0;
}
poj2096
题意:
一个软件有s个子系统,会产生n种bug。某人一天发现一个bug,出现在某个子系统的概率是1/s,属于某种类型的概率是1/n。求找到所有的n种bug,且每个子系统都找到bug,这样所要的天数的期望。
思路
状态表示:dp[i][j]表示已经找到i种bug,并存在于j个子系统中,要达到目标状态的天数的期望。
显然,dp[n][s]=0,因为已经达到目标了。而dp[0][0]就是我们要求的答案,即还没有找到任何bug的情况下到达dp[n][s]时需要的期望天数。
从dp[i][j]开始,后面一天找到的1个bug,可以转化成以下四种:
(1)dp[i][j] 发现一个bug属于已经找到的i个分类和j个子系统中(这一天相当于浪费了)
(2)dp[i+1][j] 发现一个bug属于新的分类,但属于已经找到的j种子系统
(3)dp[i][j+1] 发现一个bug属于已经找到的i个分类,但不属于已有的子系统
(4)dp[i+1][j+1]发现一个bug属于新的分类和新的一个子系统
以上四种的概率分别为:
p1 = i*j / (n*s)
p2 = (n-i)*j / (n*s)
p3 = i*(s-j) / (n*s)
p4 = (n-i)*(s-j) / (n*s)
期望可以分解成多个子期望的加权和,权为子期望发生的概率,即 E(aA+bB+…) = aE(A) + bE(B) +…
所以:
dp[i,j] = p1*dp[i,j] + p2*dp[i+1,j] + p3*dp[i,j+1] + p4*dp[i+1,j+1] + 1;//天数加1
整理得:
dp[i,j] = ( 1 + p2*dp[i+1,j] + p3*dp[i,j+1] + p4*dp[i+1,j+1] )/( 1-p1 )
整理得:
dp[i,j] = ( 1 + p2*dp[i+1,j] + p3*dp[i,j+1] + p4*dp[i+1,j+1] )/( 1-p1 )
= ( n*s + (n-i)*j*dp[i+1,j] + i*(s-j)*dp[i,j+1] + (n-i)*(s-j)*dp[i+1,j+1] )/( n*s - i*j )
#include <cstdio>
#include <iostream>
using namespace std;
double dp[1005][1005];
int main()
{
int n, s, ns;
cin >> n >> s;
ns = n*s;
//从dp[n][s]倒推到dp[0][0],dp[0][0]就是答案
for (int i = n; i >= 0; i--)
for (int j = s; j >= 0; j--)
{
if ( i == n && j == s )
dp[n][s]=0.0;
else
dp[i][j] = ( ns + (n-i)*j*dp[i+1][j] + i*(s-j)*dp[i][j+1] + (n-i)*(s-j)*dp[i+1][j+1] )/( ns - i*j );
}
printf("%.4f\n", dp[0][0]);
return 0;
}
zoj3329
题意:
有三个均匀的骰子,分别有k1,k2,k3个面,初始分数是0,当掷三个骰子的点数分别为a,b,c的时候,分数清零,否则分数加上三个骰子的点数和,当分数>n的时候结束。求需要掷骰子的次数的期望。
思路
设dp[i]表示达到i分时到达目标状态的步数期望,pk为投掷k分的概率,p0为回到0的概率
则dp[i]=∑(pk*dp[i+k])+dp[0]*p0+1; (1)
由上式发现每个 dp[i]都包含 dp[0],都和dp[0]有关系,而且dp[0]就是我们所求,为常数
设dp[i]=A[i]*dp[0]+B[i];---(2)
(1)代入上述方程右边得到:
dp[i]=∑(pk*A[i+k]*dp[0]+pk*B[i+k])+dp[0]*p0+1
=(∑(pk*A[i+k])+p0)dp[0]+∑(pk*B[i+k])+1;---(3)
对比(2),(3),
A[i]=(∑(pk*A[i+k])+p0)
B[i]=∑(pk*B[i+k])+1
先递推求得A[0]和B[0].
那么 dp[0]=B[0]/(1-A[0]);
#include<iostream>
#include<cstring>
using namespace std;
const int N=510;
double A[N],B[N];
double p[20];
int main()
{
int T;
int k1,k2,k3,a,b,c;
int n;
cin>>T;
while(T--)
{
cin>>n>>k1>>k2>>k3>>a>>b>>c;
memset(p,0,sizeof p);
for(int i=1;i<=k1;i++)
for(int j=1;j<=k2;j++)
for(int k=1;k<=k3;k++)
if(i == a && j ==b && k == c)
continue;
else
p[i+j+k]+=1.0/(k1*k2*k3);//求i+j+k的概率
memset(A,0,sizeof A);
memset(B,0,sizeof B);
for(int i=n;i>=0;i--)
{
A[i]=1.0/(k1*k2*k3),B[i]=1;
for(int j=3;j<=k1+k2+k3;j++)
{
A[i]+=A[i+j]*p[j];
B[i]+=B[i+j]*p[j];
}
}
printf("%.15f\n",B[0]/(1-A[0]));
}
return 0;
}
总结下这类概率DP:
既DP[i]可能由DP[i+k]和DP[i+j]需要求的比如DP[0]决定
相当于概率一直递推下去会回到原点
比如
(1):DP[i]=a*DP[i+k]+b*DP[0]+d*DP[i+j]+c;
但是DP[i+k]和DP[0]都是未知
这时候根据DP[i]的方程式假设一个方程式:
比如:
(2):DP[i]=A[i]*DP[i+k]+B[i]*DP[0]+C[i];
因为要求DP[0],所以当i=0的时候但是A[0],B[0],C[0]未知
对比(1)和(2)的差别
这时候对比(1)和(2)发现两者之间的差别在于DP[i+j]
所以根据(2)求DP[i+j]然后代入(1)消除然后对比(2)就可以得到A[i],B[i],C[i]
然后视具体情况根据A[i],B[i],C[i]求得A[0],B[0],C[0]继而求DP[0]
迷宫概率
hdu4035
题意:
有n个房间,由n-1条隧道连通起来,实际上就形成了一棵树,从结点1出发,开始走,在每个结点i都有3种可能:
1.被杀死,回到结点1处(概率为ki)
2.找到出口,走出迷宫 (概率为ei)
3.和该点相连有m条边,随机走一条
求:走出迷宫所要走的边数的期望值。
分析
一棵树,一个人初始在1号点,每次到达一个点,有$k_i$的概率被杀死,并且回到1号点,有$e_i$的概率直接逃离
然后等概率的逃到与他相邻的节点$\frac{1−k_i−e_i}{deg[i]}$,(deg[i]为i结点的度数),这种情况下每次移动步数+1,求逃出去的期望步数。
定义dp状态E[i]: 在结点i处,逃离迷宫所要走的步数期望,E[1]就是答案
设我们的目标的0号结点,E[0]=0, 倒推
(1)对于叶子结点,有三个去向:父结点,死掉,逃离
$E[i]=(1−k_i−e_i)∗(E[fa[i]]+1)+k_i∗E[1]+E[0]∗e_i$
$E[i]=(1−k_i−e_i)∗E[fa[i]]+k_i∗E[1]+(1−k_i−e_i)$
在这个式子中E[fa],E[1]是未知量,那么我们呢可以把式子化简为:
$E[i]=A[i]∗E[fa[i]]+B[i]∗E[1]+C[i]$
(2)对于非叶子结点,也是三个去向:继续前进,死掉,逃离
$E[i]=(E[fa[i]]+1)∗\frac{1−ki−ei}{deg[i]}+∑(E[son[i]]+1)∗\frac{1−k_i−e_i}{deg[i]}+k_i∗E[1]+E[0]∗e_i$
$E[i]=(E[fa[i]]+1+∑(E[son[i]]+1))∗\frac{1−k_i−e_i}{deg[i]}+k_i∗E[1]$
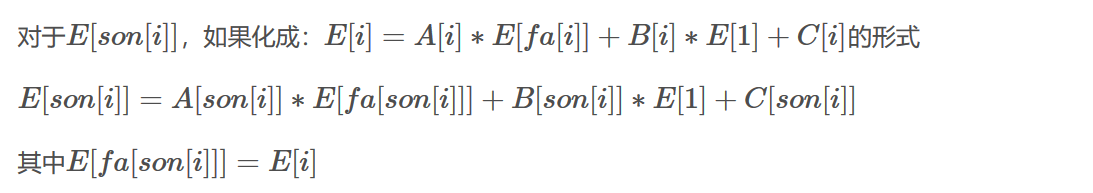
消去E[son[i]]
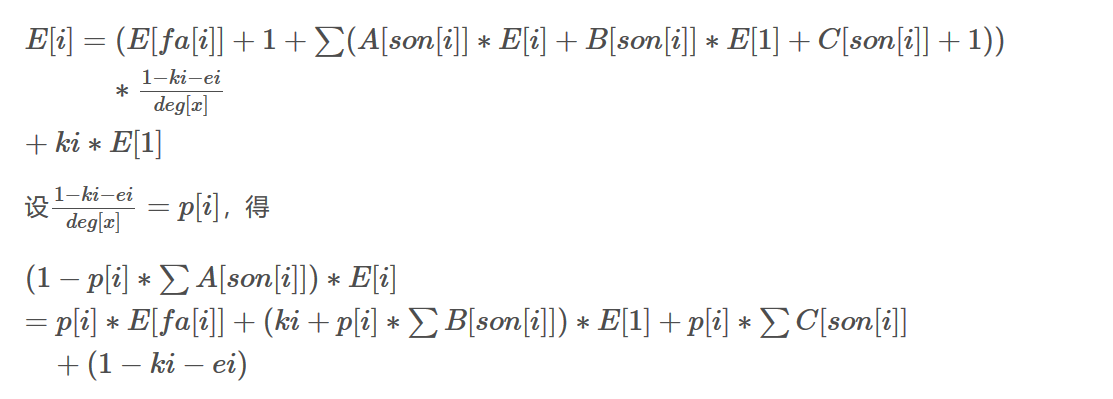
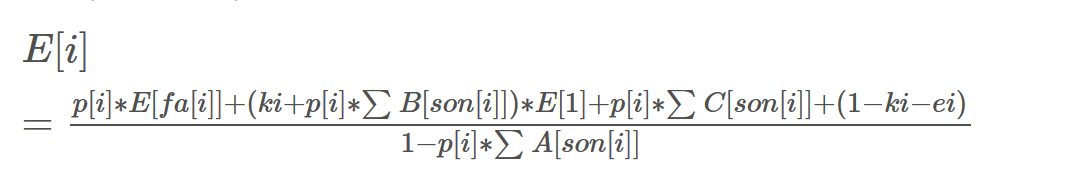
常数项中的$(1−k_i−e_i)$,实际上是$p[i]∗(1+\sum_{1}^{son[i]} {1})$(子结点数+父节点到该点的一条边)
终于推完了QAQ
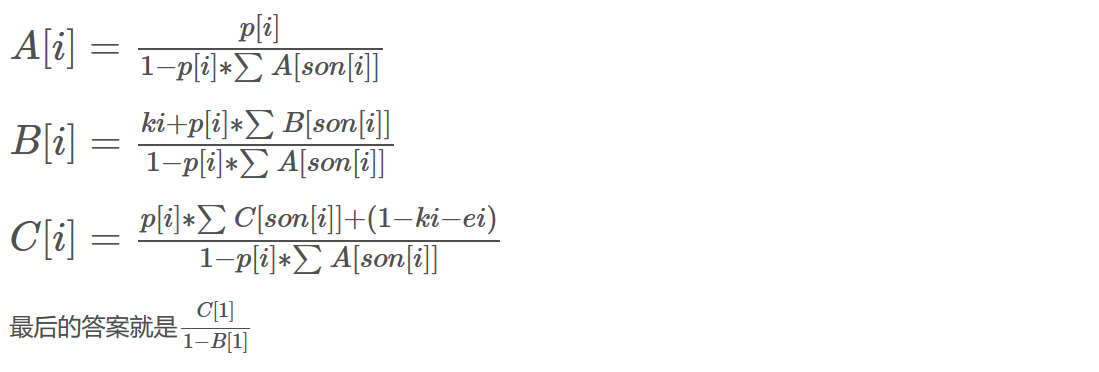
对于叶子结点
$A_i = 1 - k_i - e_i$;
$B_i = k_i$;
$C_i = 1 - k_i - e_i$;
可以看出,计算过程是从叶子结点开始算的,在算他们的父节点,直到算出根节点的$A_1,B_1,C_1$,得到E[1];
从叶子结点到根节点的顺序遍历每个点,用DFS,从根节点1出发,DFS到最底层的叶子结点,计算叶子结点$A_i,B_i,C_i$,然后逐步回退,在计算非叶子结点$A_i,B_i,C_i$
#include<iostream>
#include<algorithm>
#include<cstring>
#include<cstdio>
using namespace std;
const int N=10010;
int n,m;
vector<int> v[N];
double k[N],e[N];
const int eps=1e-10;
double A[N],B[N],C[N],p[N];
int h[N],edge[N<<1],ne[N<<1],idx;
int deg[N];
void add(int a,int b)
{
edge[idx]=b,ne[idx]=h[a],h[a]=idx++;
}
bool dfs(int u,int fa)
{
double sumA=0,sumB=0,sumC=0;
int cnt=0;
for(int i=h[u];~i;i=ne[i])
{
int j=edge[i];
if(j == fa)
continue;
if(!dfs(j,u))
return false;
sumA+=A[j];
sumB+=B[j];
sumC+=C[j];
cnt++;
}
if(cnt == 0)
{
A[u]=1-k[u]-e[u];
B[u]=k[u];
C[u]=1-k[u]-e[u];
return true;
}
double t=1-sumA*p[u];
if(fabs(t)<eps)
return false;
A[u]=p[u]/t;
B[u]=(k[u]+p[u]*sumB)/t;
C[u]=(p[u]*sumC+(1-k[u]-e[u]))/t;
return true;
}
int main()
{
int T;
cin>>T;
for(int kase=1;kase<=T;kase++)
{
scanf("%d",&n);
// for(int i=1;i<=n;i++)
// v[i].clear();
memset(h,-1,sizeof h);
memset(deg,0,sizeof deg);
idx=0;
for(int i=1;i<n;i++)
{
int a,b;
cin>>a>>b;
// v[a].push_back(b);
// v[b].push_back(a);
add(a,b);
add(b,a);
deg[a]++,deg[b]++;
}
for(int i=1;i<=n;i++)
{
scanf("%lf%lf",&k[i],&e[i]);//killed and exit
k[i]/=100.0;
e[i]/=100.0;
//cout<<"----"<<k[i]<<' '<<e[i]<<endl;
//m=v[i].size();
p[i]=(1-k[i]-e[i])/deg[i];
//cout<<"--"<<p[i]<<endl;
}
cout<<"Case "<<kase<<": ";
if(dfs(1,-1) && fabs(1-B[1]) > eps)
printf("%.6f\n",C[1]/(1-B[1]));
else
printf("impossible\n");
}
return 0;
}
补两道简单题:
lightoj1265
题意:
你和n个老虎,m个鹿,被困在一座岛上,每两个物种随机相遇,老虎和老虎相遇则会减少两个老虎,老虎和鹿相遇则会减少一个鹿,人和老虎相遇则人直接死亡,人和鹿相遇,可以自行选择是否杀鹿,问最后没有老虎并且人成功存活的概率
(1)dp法
dp[i][j] 表示 i个tiger,j个deer时人存活的概率。
考虑到五种情况,利用全概率公式,得出状态转移方程:
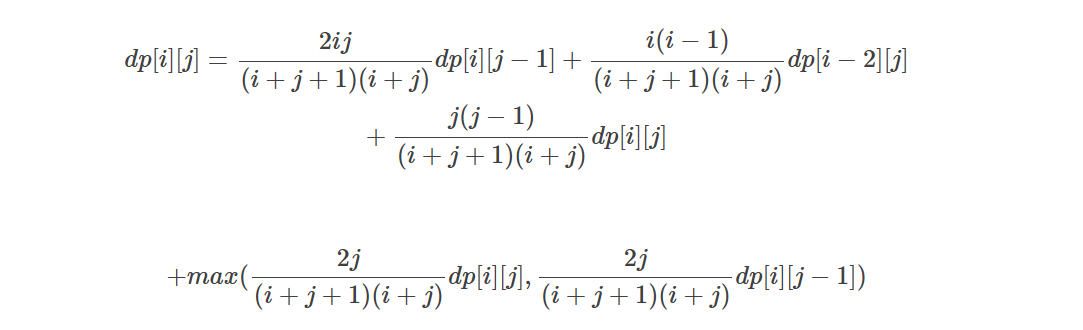
边界:dp[0][i] = 1(无tiger时人活的概率为1,正推
#include<iostream>
using namespace std;
double dp[1010][1010];
int main()
{
int T;
scanf("%d", &T);
for(int kase=1;kase<=T;kase++)
{
int t, d;
scanf("%d%d", &t, &d);//tiget and deer
for (int i = 0; i <= t; ++i)
for (int j = 0; j <= d; ++j)
dp[i][j] = 0.0;
for (int i = 0; i <= d; ++i)
dp[0][i] = 1.0;
for (int i = 1; i <= t; ++i)
for (int j = 0; j <= d; ++j)
{
double r1 = 0, r2 = 0;
if (i >= 2)//虎虎
r1 += dp[i - 2][j] * (i * (i - 1)) * 1.0 / ((i + j + 1) * (i + j));
if (j >= 1)//虎鹿or鹿虎
r1 += dp[i][j - 1] * (i * j * 2.0 / ((i + j + 1) * (i + j)));
double p = 0;
if (j >= 2)//鹿鹿
p = (j * (j - 1) * 1.0) / ((i + j + 1) * (i + j));
if (j >= 1)
{
r2 = r1;
r2 += j * 2.0 / ((i + j + 1) * (i + j)) * dp[i][j - 1];
r2 /= (1 - p);
}
r1 /= (1 - p - j * 2.0 / ((i + j + 1) * (i + j)));
dp[i][j] = max(r1, r2);
}
printf("Case %d: %.6f\n", kase, dp[t][d]);
}
return 0;
}
(2)性质法
如果老虎为0 则人活得概率为1
如果老虎为奇数,因为只有两只老虎相遇的时候老虎才能死,所以必然是两个两个一起死,最后必然剩一只老虎 所以人活得概率为0
如果老虎为偶,每天不让老虎和人相遇即可,等到所有老虎都相遇互相残杀,人就是活的,而且鹿的数量 并不能影响人的存活率 ,因为鹿并不能减少老虎的数量
所以 ,如果老虎为偶数,则我们把所有老虎都相遇的概率求出来即可
设tiger有x个
则一对老虎相遇的概率为 $\frac{C_x^1}{(x+1)}\times\frac{C_{x-1}^1}{x}$
所有老虎相遇的概率为 $\frac{C_x^1}{x+1}\times\frac{C_{x-1}^1}{x}\times\frac{C_{x-2}^1}{x-1}\times\frac{C_{x-3}^1}{x-2}\times......\times\frac{C_2^1}{(3)}\times\frac{C_1^1}{2}$化简为 $\frac{1}{x+1}$
#include<bits/stdc++.h>
using namespace std;
int t,n,m;
int main()
{
scanf("%d",&t);
int cas=0;
while(t--)
{
scanf("%d%d",&n,&m);
double ans=0;
if(n%2==0)
ans=1.0/(n+1);
printf("Case %d: %.8lf\n",++cas,ans);
}
return 0;
}
lightoj1274
题意:
有n个题目,对应n个答案分别为yes或no,yes为3bytes,no为2bytes,s表示所有答案总的byte大小,根据所给的条件,很容易得出有多少个yes和no。
接下来你要做的事就是猜答案,那么你猜答案的规则是把某个可能的答案序列拿出来,在首位加上一个yes,去掉最后一个,再用得到的答案序列与可能的答案序列进行比较,某一个答案不相同表示一个错误答案。
题目要求输出的是错误答案个数的期望。
思路
我们简化一下,yes和no可以简化为1 和 0,这个题的意思就是你已知1和0的个数,这些排列你随心定,在你写出的01串之前加上一个1,问你两个01串的不匹配数(比如说你拟出来的串是0100,首部加上一个1得到的串是10100,当然最后一个0是不用参与匹配的,相当于0100串与1010串比较得到不匹配的字符数)该匹配是自身匹配,相当于前一个字符与后一个字符对比,如果是不同字符不能匹配数就+1
毫无疑问,最开始我们要做的工作就是先通过输入数据求出1和0的个数,设a为1的个数,b为0的个数,我们要构造一个具有a个1的01字符串,字符串长度为n,在每一次添字符的时候都有两种可能(当还能添1的时候)0和1。
状态表示:dp[i][j][k],表示第i位使用了j个yes下一位输出yes(k=0)或no(k=1)的期望,期望使用逆推
因为可以预先求出yes和no的个数,那么当前第i位输出yes的期望即为i+1位输出yes的期望与i+1位输出no的期望+1然后分别乘以出现的概率
状态转移:
dp[i][j][1] = dp[i+1][j+1][1]p1 + (dp[i+1][j][0]+1)p2;当前后匹配不上的时候,dp需要加一
dp[i][j][0] = (dp[i+1][j+1][1]+1)p1 + dp[i+1][j][0]p2;
p1表示下一位输出yes的概率,p0表示下一位输出no的概率
#include<cstdio>
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N=5010;
int n,s;
double dp[2][N][2];//滚动数组
int main()
{
int T;
scanf("%d",&T);
for(int kase=1; kase<=T; ++kase)
{
scanf("%d%d",&n,&s);
int yes = s-2*n, no = 3*n-s;
memset(dp,0,sizeof(dp));
for(int i=n-1; i>=0; --i)
{
int R = min(yes,i), L = max(i-no,0);
for(int j=R; j>=L; --j)
{
double p1 = 1.0*(yes-j)/(n-i), p0 = 1.0*(no-(i-j))/(n-i);
//cout<<p1<<' '<<p0<<endl;
dp[i&1][j][1] = dp[i+1&1][j+1][1]*p1 + (dp[i+1&1][j][0]+1)*p0;
dp[i&1][j][0]= (dp[i+1&1][j+1][1]+1)*p1 + dp[i+1&1][j][0]*p0;
}
}
printf("Case %d: %.10f\n",kase,dp[0][0][1]);
}
return 0;
}


tql