更好的阅读体验

搜索算法

算法类型

搜索算法有很多种类型,一般来说就是深度优先搜索,广度优先搜索,A*搜索,IDA*搜索这种类型的搜索,而本讲义讲述的就是其中最核心,最简单的搜索深度优先搜索和广度优先搜索.

DFS算法简述

首先深度优先搜索,是一种适用于树形结构的搜索.它和数据结构栈紧密相连.
对于这种算法而言,它主要的步骤大致如下所示:
1. 找到当前可以拓展的点,那么立即走入这个分支点.
2. 如果当前搜索分支,无效或者已经找到目标,那么退回到上一步,即回溯.
3. 每一个点最多会被访问两次.访问含义是入栈一次,出栈一次.

DFS性质

DFS序列就是深度优先搜索最为重要的性质,它可以将一个子树变成一个区间.

BFS算法简述

BFS算法,即广度优先搜索,它和深度优先搜索恰恰相反,它是一种适用于图型结构的搜索,它和数据结构队列紧密向量.
对于这种算法而言,它主要的步骤大致如下所示:
1. 找到当前可以拓展的点,将它放入候选队列之中.
2. 每次选取候选队列的队头,作为当前状态.

BFS性质

对于广度优先搜索而言,它是一种逐层遍历的算法,所有状态按照入队的先后顺序具有层次单调性,也就是所谓的步数单调性质,如果每一次拓展恰好对应一部,那么当第一个状态第一次被访问(入队),就会得到从起始状态到达该状态的最少步数.

by Lyd大佬

第一题(dfs)

原题连接

题目描述

有一个$m \times m$的棋盘，棋盘上每一个格子可能是红色、黄色或没有任何颜色的。你现在要从棋盘的最左上角走到棋盘的最右下角。

任何一个时刻，你所站在的位置必须是有颜色的（不能是无色的）， 你只能向上、 下、左、 右四个方向前进。当你从一个格子走向另一个格子时，如果两个格子的颜色相同，那你不需要花费金币；如果不同，则你需要花费 $1 $个金币。

另外， 你可以花费 $2$ 个金币施展魔法让下一个无色格子暂时变为你指定的颜色。但这个魔法不能连续使用， 而且这个魔法的持续时间很短，也就是说，如果你使用了这个魔法，走到了这个暂时有颜色的格子上，你就不能继续使用魔法； 只有当你离开这个位置，走到一个本来就有颜色的格子上的时候，你才能继续使用这个魔法，而当你离开了这个位置（施展魔法使得变为有颜色的格子）时，这个格子恢复为无色。

现在你要从棋盘的最左上角，走到棋盘的最右下角，求花费的最少金币是多少？

输入输出格式

输入格式：

第一行包含两个正整数$ m, n$，以一个空格分开，分别代表棋盘的大小，棋盘上有颜色的格子的数量。

接下来的$ n $行，每行三个正整数$ x, y, c$， 分别表示坐标为$(x,y)$的格子有颜色$ c$。

其中$ c=1$ 代表黄色，$ c=0$ 代表红色。 相邻两个数之间用一个空格隔开。 棋盘左上角的坐标为$(1, 1)$，右下角的坐标为$( m, m)$。

棋盘上其余的格子都是无色。保证棋盘的左上角，也就是$(1, 1)$ 一定是有颜色的。

输出格式：

一个整数，表示花费的金币的最小值，如果无法到达，输出$-1$。

输入输出样例

输入样例#1：

复制

5 7
1 1 0
1 2 0
2 2 1
3 3 1
3 4 0
4 4 1
5 5 0

输出样例#1：

8

输入样例#2：

5 5
1 1 0
1 2 0
2 2 1
3 3 1
5 5 0

输出样例#2：

-1

说明

输入输出样例 1 说明

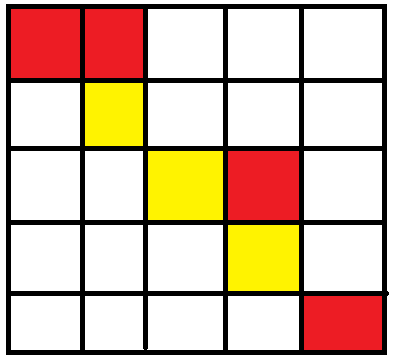
从$(1,1)$开始，走到$(1,2)$不花费金币

从$(1,2)$向下走到$(2,2)$花费 $1$ 枚金币

从$(2,2)$施展魔法，将$(2,3)$变为黄色，花费 $2$ 枚金币

从$(2,2)$走到$(2,3)$不花费金币

从$(2,3)$走到$(3,3)$不花费金币

从$(3,3)$走到$(3,4)$花费 $1$ 枚金币

从$(3,4)$走到$(4,4)$花费 $1$ 枚金币

从$(4,4)$施展魔法，将$(4,5)$变为黄色，花费$ 2$ 枚金币，

从$(4,4)$走到$(4,5)$不花费金币

从$(4,5)$走到$(5,5)$花费 $1$ 枚金币

共花费 $8 $枚金币。

输入输出样例 2 说明

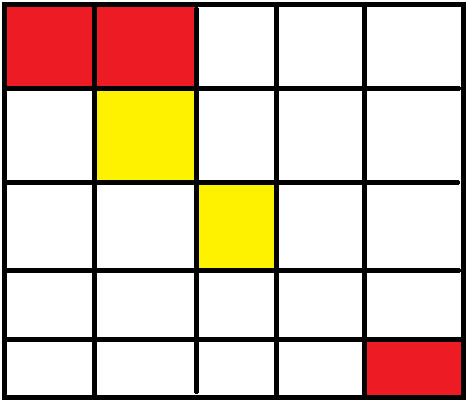
从$( 1, 1)$走到$( 1, 2)$,不花费金币

从$( 1, 2)$走到$( 2, 2)$,花费$ 1 $金币

施展魔法将$( 2, 3)$变为黄色,并从$( 2, 2)$走到$( 2, 3)$花费$ 2$ 金币

从$( 2, 3)$走到$( 3, 3)$不花费金币

从$( 3, 3)$只能施展魔法到达$( 3, 2),( 2, 3),( 3, 4),( 4, 3)$

而从以上四点均无法到达$( 5, 5)$,故无法到达终点,输出$-1$

数据规模与约定

对于 $30\%$的数据, $1 \le m \le 5, 1 \le n \le 10$。

对于 $60\%$的数据, $1 \le m \le 20, 1 \le n \le 200$。

对于 $100\%$的数据, $1 \le m \le 100, 1 \le n \le 1,000$。

解题报告

题意理解

这道题目的一句话题意是:

让你从$(1,1)$走到$(m,m)$,要求路上的花费代价最少.
如果你从A走到B,那么走一步的代价有三种:
1. 若方格A的颜色等于方格B的颜色,那么花费代价为0
2. 若方格A的颜色不同于方格B的颜色,那么花费代价为1.
3. 若方格B的颜色为无色,那么相当于使用一次魔法,且花费的代价为2,并且下一步不可以使用魔法.

判断算法

一般来说,我们面对类似于迷宫这类,也就是具有非常明确的图像显示的题目,而言我们需要第一时间思考到这道题目是不是要用到搜索算法

算法选择

搜索的算法有很多种.比如说深度优先搜索,广度优先搜索,A搜索,IDA搜索,但是对于$m \le 100$的数据范围,而言我们并不需要多么高级的搜索,只需要一点点记忆化剪枝+深度优先搜索即可

思路确定

首先对于一道搜索题目而言的话,我们有基本的三点目标

目标一:方向指示数组,这个数组在迷宫问题中,你可以认为是走路方式,在动态规划问题中,你可以认为是拓展状态的决策.

目标二:边界处理,对于这道题目而言,边界处理其实很简单,就是在指定的区域里面而已.也就是 $(x,y)$ 不越界

目标三:拓展准则,一道题目而言我们不仅仅要满足边界处理,还有更为重要,也就是这道题目的最重要的一点,如何判断我们走这一步是满足条件的.以及这一步花费的代价

细节处理

目标三处理是我们这道题目的核心关键,也就是不同于其他问题的一个难点.下面我会详细的说明.

1. 上一次使用了魔法,那么这一次不能使用魔法
2. 上一次使用了魔法,判断上一个点是不是和当前点颜色一致
3. 颜色相同则不需要花费代价,否则花费1点代价
4. 拓展的点是无颜色,那么我们必须使用魔法,并且花费两点代价

代码演示

#include <bits/stdc++.h>
using namespace std;
const int N=1100;
const int dx[4]= {1,-1,0,0};
const int dy[4]= {0,0,1,-1};
int g[N][N],n,m,dis[N][N],vis[N][N],ans=1e9;
int check(int x,int y)
{
    if (x<1 || x>n || y<1 || y>n || vis[x][y])//在合法的矩阵内部,而且没有访问
        return true;//一个条件不满足,则这一步无法拓展.
    return false;
}
void dfs(int x,int y,int nowc,int r)
{
    if(x==n && y==n && r<ans)
    {
        ans=r;
        return;
    }
    if(r>=dis[x][y])//如果发现当前的代码,已经大于上一次我来到这个点的代价,那么显然可以剪枝,我再怎么最优,也没有上一次最优.
        return;
    dis[x][y]=r;//记录最优值
    for(int i=0; i<4; i++)//四个拓展步骤
    {
        int xx=x+dx[i],yy=y+dy[i],cl=g[xx][yy];//拓展步骤,并且看下一步的颜色
        if (check(xx,yy))//如果不越界,而且没有走过这个点的话
            continue;
        vis[xx][yy]=true;//已经访问了
        if(nowc>=3 && cl!=0)//如果说上一次使用了魔法,但是我当前这个点不需要使用魔法的话
        {
            if((nowc+cl)%2==0)//这一步非常重要,大致意思是,这两个点颜色相同,或者上一次魔法和本宫格颜色一样.
                dfs(xx,yy,cl,r);//不需要花费代价
            else
                dfs(xx,yy,cl,r+1);//需要花费代价
        }
        else if(nowc==1 || nowc==2)//如果这个上一次没有使用魔法的话
        {
            if(cl==1 || cl==2)//当前宫格不需要使用魔法
            {
                if(nowc!=cl)//颜色不一样
                    dfs(xx,yy,cl,r+1);
                else//颜色一样
                    dfs(xx,yy,cl,r);
            }
            else
                dfs(xx,yy,nowc+2,r+2);//使用魔法
        }
        vis[xx][yy]=false;//回溯处理.
    }
}
int main()
{
    ios::sync_with_stdio(false);
    cin>>n>>m;
    memset(dis,0x3f,sizeof(dis));
    for(int i=1; i<=m; i++)
    {
        int x,y,c;
        cin>>x>>y>>c;
        g[x][y]=c+1;//习惯颜色处理.
    }
    vis[1][1]=true;//初始点已经访问了
    dfs(1,1,g[1][1],0);//开始搜索
    if (ans==1e9)//找不到合法方案
        cout<<-1;
    else
        cout<<ans;//找到了
    return 0;
}

第二题(BFS)

原题链接

题目描述

现有一块大奶酪，它的高度为 $h$，它的长度和宽度我们可以认为是无限大的，奶酪 中间有许多 半径相同 的球形空洞。我们可以在这块奶酪中建立空间坐标系，在坐标系中， 奶酪的下表面为$z = 0$，奶酪的上表面为$z = h$。

现在，奶酪的下表面有一只小老鼠 Jerry，它知道奶酪中所有空洞的球心所在的坐 标。如果两个空洞相切或是相交，则 Jerry 可以从其中一个空洞跑到另一个空洞，特别 地，如果一个空洞与下表面相切或是相交，Jerry 则可以从奶酪下表面跑进空洞；如果 一个空洞与上表面相切或是相交，Jerry 则可以从空洞跑到奶酪上表面。

位于奶酪下表面的 Jerry 想知道，在 不破坏奶酪 的情况下，能否利用已有的空洞跑 到奶酪的上表面去?

空间内两点$P_1(x_1,y_1,z_1)$、$P2(x_2,y_2,z_2)$的距离公式如下：

$$\mathrm{dist}(P_1,P_2)=\sqrt{(x_1-x_2)^2+(y_1-y_2)^2+(z_1-z_2)^2}$$

输入输出格式

输入格式：

每个输入文件包含多组数据。

的第一行，包含一个正整数 $T$，代表该输入文件中所含的数据组数。

接下来是 $T$ 组数据，每组数据的格式如下： 第一行包含三个正整数 $n,h$ 和 $r$，两个数之间以一个空格分开，分别代表奶酪中空 洞的数量，奶酪的高度和空洞的半径。

接下来的 $n$ 行，每行包含三个整数 $x,y,z$，两个数之间以一个空格分开，表示空 洞球心坐标为$(x,y,z)$。

输出格式：

$T$ 行，分别对应 $T$ 组数据的答案，如果在第 $i$ 组数据中，Jerry 能从下 表面跑到上表面，则输出Yes，如果不能，则输出No （均不包含引号）。

输入输出样例

输入样例#1：

3 
2 4 1 
0 0 1 
0 0 3 
2 5 1 
0 0 1 
0 0 4 
2 5 2 
0 0 2 
2 0 4

输出样例#1：

Yes
No
Yes

说明

【输入输出样例 1 说明】

第一组数据,由奶酪的剖面图可见：

第一个空洞在$(0,0,0)$与下表面相切

第二个空洞在$(0,0,4)$与上表面相切 两个空洞在$(0,0,2)$相切

输出 Yes

第二组数据,由奶酪的剖面图可见：

两个空洞既不相交也不相切

输出 No

第三组数据,由奶酪的剖面图可见：

两个空洞相交 且与上下表面相切或相交

输出 Yes

【数据规模与约定】

对于 $20\%$的数据,$n = 1$,$1 \le h$ , $r \le 10,000$,坐标的绝对值不超过 $10,000$。

对于 $40\%$的数据,$1 \le n \le 8$, $1 \le h$ , $r \le 10,000$,坐标的绝对值不超过 $10,000$。

对于$80\%$的数据, $1 \le n \le 1,000$, $1 \le h , r \le 10,000$,坐标的绝对值不超过$10,000$。

对于 $100\%$的数据,$1 \le n \le 1,000$,$1 \le h , r \le 1,000,000,000$,$T \le 20$,坐标的 绝对值不超过 $1,000,000,000$。

解题报告

题意理解

一句话题意:你要从最低点走到最高点,你必须从与下边界联通的洞孔开始走,而且每次只能走到和你所在奶酪相连通的奶酪.

对于两个奶酪而言,他们的距离必须小于$2 \times r$,才被认为是相通的.

空间内两点$P_1(x_1,y_1,z_1)$、$P2(x_2,y_2,z_2)$的距离公式如下：
$$\mathrm{dist}(P_1,P_2)=\sqrt{(x_1-x_2)^2+(y_1-y_2)^2+(z_1-z_2)^2}$$

条件性质

这道题目的条件就是:连通性&两点之间距离公式.
这道题目的性质:还是上面所说的连通性.即两个奶酪必须连通,才可以转移

算法判断

这道题目我们初步一看,发现特别的繁琐,然而实际上这道题目就是一道平面直角坐标系走迷宫问题.
对于走迷宫问题,显然BFS广度优先搜索是我们的不二选择.

解析算法

首先对于一道搜索题目而言的话,我们还是有基本的三点目标

目标一:方向指示数组: 对于这道题目而言,显然每一个和它相连通的洞都可以,所以这道题目的方向指示数组形同虚设.

目标二:边界处理: 对于这道题目而言,我们的坐标其实也没有什么要求,因为连通已经包含了所有的条件.

目标三:拓展准则: 每一道搜索题目,难点往往都在这个拓展准则上面,这道题目也不例外,我们发现,这道题目的拓展准则也就是题目中连通性,只要两个点是连通的,那么我们就可以拓展.

代码解析

#include <bits/stdc++.h>
using namespace std;
const int N=1e4;
struct node
{
    double x,y,z;//double类型要注意
} a[N];
int vis[N],n,h,r,t;
queue<node> q,kong;
double dist(node a,node b)//计算两点之间的距离,也就是题目描述中给出的公式.
{
    double nx=a.x-b.x,ny=a.y-b.y,nz=a.z-b.z;
    double ans=sqrt(nx*nx+ny*ny+nz*nz);
    return ans;
}
int bfs(void)
{
    while(q.size())
    {
        if (q.front().z+r>=h)//如果满足条件.
            return true;
        node now=q.front();
        q.pop();
        for(int i=1; i<=n; i++)//所有的点都可以成为下一步的拓展.
        {
            if (r*2>=dist(now,a[i]) && !vis[i])//如果两点的距离<=2*r,而且这个点没有访问过.
            {
                q.push(a[i]);//入队
                vis[i]=1;//已经访问过了
                if (q.front().z+r>=h)//如果满足条件,那么显然可以返回true
                    return true;
            }
        }
    }
    return false;//找不到合法路径
}
int main()
{
    ios::sync_with_stdio(false);//读入优化,防止超时.
    cin>>t;
    while(t--)
    {
        cin>>n>>h>>r;
        for(int i=1; i<=n; i++)
            cin>>a[i].x>>a[i].y>>a[i].z;
        q=kong;//初始化
        memset(vis,false,sizeof(vis));//初始化不可少
        for(int i=1; i<=n; i++)
            if (a[i].z-r<=0)//如果和下边界接触
                q.push(a[i]),vis[i]=1;//才可以入队
        if (bfs())//判断是否找得到合法路径
            cout<<"Yes";
        else
            cout<<"No";
        cout<<endl;
    }
    return 0;//日常必打.
}