1.Floyd
1.1 Floyd求传递闭包
acwing343
对于每个i小于j的不等式,d[i][j]=1;i大于j的式子当小于处理,除了i小于j的情况外,d[i][i]=0;
floyd作传递闭包,
若d[i][j],d[j][i]均为0,则不能确定每一变量大小关系。
d[i][j],d[j][i]有一个为1,则能能确定每一变量大小关系。
若d[i][j],d[j][i]均为1,则存在矛盾。
#include<iostream>
#include<cstring>
using namespace std;
const int N=26;
int n,m;
int d[N][N];
bool st[N];
void print()
{
for(int i=0;i<n;i++)
{
for(int j=0;j<n;j++)
cout<<d[i][j]<<' ';
cout<<endl;
}
cout<<endl;
}
void floyd()
{
for(int k=0;k<n;k++)
for(int i=0;i<n;i++)
for(int j=0;j<n;j++)
d[i][j] |=d[i][k] && d[k][j];
//print();
}
int check()
{
//存在矛盾
for(int i=0;i<n;i++)
if(d[i][i])
return 2;
//暂时无法完全判定顺序
for(int i=0;i<n;i++)
for(int j=0;j<i;j++)
if(!d[i][j] && !d[j][i])
return 0;
return 1;
}
char get_min()
{
for(int i=0;i<n;i++)
if(!st[i])
{
bool flag = true;
//判断是否存在比i更小的
for(int j=0;j<n;j++)
if(!st[j] && d[j][i])
{
flag=false;
break;
}
if(flag)
{
st[i] = true;
return i+'A';
}
}
}
int main()
{
while(cin>>n>>m && n)
{
memset(d,0,sizeof d);
int type=0,t;//t为0表示还不能确定所有大小关系,t为1表示已经完全确定所有关系,t为2表示存在矛盾)
for(int i=1;i<=m;i++)
{
char op[5];
cin>>op;
int a=op[0]-'A';
int b=op[2]-'A';
if(!type)//无法完全判定所有字母顺序的情况下继续循环
{
d[a][b]=1;
floyd();
type=check();
if(type)
{
t=i;
}
}
}
if(!type)
puts("Sorted sequence cannot be determined.");
else if (type == 2) printf("Inconsistency found after %d relations.\n", t);
else
{
memset(st,false,sizeof st);
printf("Sorted sequence determined after %d relations: ", t);
for(int i=0;i<n;i++)
printf("%c",get_min());//每次从还未标记的字母中选择顺序最小的一个输出
printf(".\n");
}
}
return 0;
}
例题
luoguP1119
floyd算法的主要思路,就是通过其他的点进行中转来求的两点之间的最短路。因为我们知道,两点之间有多条路,如果换一条路可以缩短距离的话,就更新最短距离。而它最本质的思想,就是用其他的点进行中转,从而达到求出最短路的目的。
那么,如何进行中转呢?两点之间可以由一个点作为中转点更新最短路径,也可以通过多个点更新最短路径。
for(k=1;k<=n;k++)
for(i=1;i<=n;i++)
for(j=1;j<=n;j++)
g[i][j]=min(g[i][j],g[i][k]+g[k][j]);
这段代码的基本思想就是:最开始只允许经过1号顶点进行中转,接下来只允许经过1和2号顶点进行中转……允许经过1~n号所有顶点进行中转,求任意两点之间的最短路程。用一句话概括就是:从i号顶点到j号顶点只经过前k号点的最短路程。
而我们再回头看题意:
所有的边全部给出,按照时间顺序更新每一个可用的点(即修建好村庄),对于每个时间点进行两点之间询问,求对于目前建设的所有村庄来说任意两点之间的最短路
不正好就是Floyd算法中使用前k个节点更新最短路的思维吗?
于是到了这里,我们差不多也就知道这题如何写了。
出题人还是很良心的,保证所有的数据都是用时间顺序给出的,所以我们只用读取+操作就可以了,不用再储存+排序。
总结:
读入,存下每个村庄修复的时间
读入所有的边并使用邻接矩阵存图
初始化
对于每次询问,将在当前时间前的所有点全部用Floyd更新。
特殊判断并输出
#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
const int N=210,INF=0x3f3f3f3f;
int g[N][N];
int n,m,q;
int tim[N];
void floyd(int k)
{
for(int i=0;i<n;i++)
for(int j=0;j<n;j++)
g[i][j]=min(g[i][j],g[i][k]+g[k][j]);
}
int main()
{
cin>>n>>m;
for(int i=0;i<n;i++)
cin>>tim[i];
memset(g,0x3f,sizeof g);
while(m--)
{
int a,b,c;
cin>>a>>b>>c;
g[a][b]=g[b][a]=min(g[a][b],c);
}
cin>>q;
int k=0;
while(q--)
{
int x,y,z;
cin>>x>>y>>z;
while(tim[k]<=z && k<n)
{
floyd(k);
k++;
}
if(g[x][y] == INF || tim[x] > z || tim[y] > z)
puts("-1");
else
cout<<g[x][y]<<endl;
}
return 0;
}
hdu3631
每次标记一个点,就以这个点作为中间结点,缩短一下任意两点节点之间的距离。
#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
const int N=310,INF=0x3f3f3f3f;
int g[N][N];
int n,m,q;
bool mark[N];
void floyd(int k)
{
for(int i=0;i<n;i++)
for(int j=0;j<n;j++)
g[i][j]=min(g[i][j],g[i][k]+g[k][j]);
}
int main()
{
int kase=1;
while(cin>>n>>m>>q && n)
{
for(int i=0;i<n;i++)
for(int j=0;j<n;j++)
if(i == j)
g[i][j]=0;
else
g[i][j]=INF;
memset(mark,0,sizeof mark);
while(m--)
{
int a,b,c;
cin>>a>>b>>c;
g[a][b]=min(g[a][b],c);
}
if(kase != 1)
cout<<endl;
printf("Case %d:\n",kase++);
while(q--)
{
int op,x,y;
cin>>op;
if(op == 0)
{
cin>>x;
if(mark[x])
printf("ERROR! At point %d\n",x);
else
{
mark[x]=true;
floyd(x);
}
}
else
{
cin>>x>>y;
if(!mark[x] || !mark[y])
printf("ERROR! At path %d to %d\n",x,y);
else if(g[x][y] == INF)
printf("No such path\n");
else
cout<<g[x][y]<<endl;
}
}
}
return 0;
}
hdu1385
floyd打印路径,要求字典序最小
#include<iostream>
#include<cstring>
#include<cstdio>
#include<algorithm>
#include<map>
#include<queue>
#include<stack>
#include<sstream>
#include<set>
#include<bitset>
#include<vector>
#include<cmath>
using namespace std;
#define ios ios::sync_with_stdio(false)
#define fi first
#define se second
const double pi=acos(-1.0);
int dx[]={-1,0,1,0,0},dy[]={0,1,0,-1,0};
typedef long long LL;
typedef pair<int,int> PII;
const int INF=0x3f3f3f3f;
const LL LNF=0x3f3f3f3f3f3f3f3f;
const int mod=13331;
const int N=110;
int g[N][N];
int path[N][N];
int c[N];
int n;
void floyd()
{
for(int k=1;k<=n;k++)
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
if(g[i][j] > g[i][k]+g[k][j]+c[k])
{
g[i][j]=g[i][k]+g[k][j]+c[k];
path[i][j]=path[i][k];
}
else if(g[i][j] == g[i][k]+g[k][j]+c[k] && path[i][j] > path[i][k])
path[i][j]=path[i][k];
}
void print_path(int a,int b)
{
if(a == b)
{
printf("%d",b);
return;
}
int k=path[a][b];
printf("%d-->",a);
print_path(k,b);
}
int main()
{
while(cin>>n)
{
if(!n) break;
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
{
scanf("%d",&g[i][j]);
if(g[i][j] == -1) g[i][j]=INF;
path[i][j]=j;
}
for(int i=1;i<=n;i++) scanf("%d",&c[i]);
floyd();
int st,ed;
while(cin>>st>>ed)
{
if(st == -1 && ed == -1) break;
printf("From %d to %d :\n",st,ed);
printf("Path: ");
print_path(st,ed);
printf("\n");
printf("Total cost : %d\n\n",g[st][ed]);
}
}
//system("pause");
}
1.2 Floyd求最小环
acwing344/hdu1599
题意:
给出n个点,至少包含三个节点的最小环。
题解
Floyd 的改进写法可以解决最小环问题,时间复杂度依然是 O(n^3),储存结构也是邻接矩阵。
1 定义:
通常来说最小环是针对有向图而言
从一个点出发,经过一条简单路径回到起点成为环.图的最小环就是所有环中长度最小的.
有向图:
1.直接用 flody 算法求到到个点得最短路,最后取 i==j 中的最小值或最大值极为最 小环和最大环的值, 注意初始化的时候将距离初始化为无穷大。
#include <iostream>
#include <cstring>
#include <cstdio>
#include <queue>
using namespace std;
const int INF=0x3f3f3f3f;
int mp[105][105];
int n,m;
int floyd()
{
int i,j,k;
for(k=0; k<n; k++)
for(i=0; i<n; i++)
for(j=0; j<n; j++)
if(mp[i][j] > mp[i][k]+mp[k][j])
mp[i][j]=mp[i][k]+mp[k][j];
}
int main()
{
int cases;
scanf("%d",&cases);
while(cases--)
{
int a,b,c;
scanf("%d %d",&n,&m);
for(int i=0; i<n; i++)
for(int j=0; j<n; j++)
mp[i][j]=INF;
for(int i=0; i<m; i++)
{
scanf("%d %d %d",&a,&b,&c);
mp[a][b]=min(mp[a][b],c);
}
floyd();
int result=INF;
for(int i=0; i<n; i++)
{
result=min(result,mp[i][i]);
}
if(result == INF)
printf("-1\n");
else
printf("%d\n",result);
}
return 0;
}
无向图
无向图的最小环的求法不可能和有向图的求法一样, 因为在有向图中 i –>j 和 j –>i 算 是一个环,但在无向图中不是一个环, 如果直接用 floyd 算法将会出错, 有向图的环可以为 2 个顶点,而无向图的环至少要3个顶点; 所以为了求无向图的最小环, 我们采用的原理是: 枚举最大环中的连接点,更新环的权重;
void floyd()
{
int i, j, k;
for(k = 1; k <= N; k++) //枚举最小环的最大编号
{
for(i = 1; i <= k - 1; i++) //因为我们是枚举最大编号的点, 所以这里只需枚举编号小于 k 的点
for(j = i + 1; j <= k - 1; j++) // 为什么 j = i+1 ?因为是为了避免一条边计算两 次并且 i == j 时因为权重为 0 会出错
{
int temp = graph[i][j] + weight[i][k] + weight[j][k];
if(temp < minLen) minLen = temp;
}
// 更新整个图的最短路径
for(i = 1; i <= N; i++)
for(j = 1; j <= N; j++)
if (g[i][j] > g[i][k] + g[k][j])
graph[i][j] = g[i][k] + g[k][j];
}
}
Floyd 算法保证了最外层循环到 k 时所有顶点间已求得以 0…k-1 为中间点的最短路径。一个环至少有3个顶点,设某环编号最大的顶点为 L ,在环中直接与之相连的两个顶点编号分别为 i 和 j (i,j < L),则最大编号为 k 的最小环长度即为 Graph(i,L) + Graph(L,j) + Dist(i,j) ,其中 Dist(i,j) 表示以 0…L-1号顶点为中间点时的最短路径,G为原图中边的权值,这时候的环为 [ i 到 j(1 < i, j <= L - 1) 的最短路径] + 边 [i, L] + 边[L, j]。刚好符合 Floyd 算法最外层循环到 k=L 时的情况(dist[i][j]=dist[i][k]+dist[k][j],k为i->j的路径中不算i,j的中间点里的最大值),对 i 和 j 循环所有编号小于 L 的顶点组合即可找到最大编号为 L 的最小环,再经过最外层 k 的循环,即可找到整个图的最小环。枚举k, i, j即可得到最小的答案。
路径的求法:
当出现需要更新的时候 ,则将 pre[i][j] = k;
核心代码:
void get_path(int i, int j)
{
if (pre[i][j] == 0)
return;
int k = pre[i][j];
get_path(i, k);
ans[cnt ++ ] = k;
get_path(k, j);
}
完整代码
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 110, INF = 0x3f3f3f3f;
int n, m;
int d[N][N], g[N][N];
int pre[N][N];
int ans[N],cnt;
void get_path(int i, int j)
{
if (pre[i][j] == 0)
return;
int k = pre[i][j];
get_path(i, k);
ans[cnt ++ ] = k;
get_path(k, j);
}
int main()
{
cin >> n >> m;
memset(g, 0x3f, sizeof g);
for (int i = 1; i <= n; i ++ )
g[i][i] = 0;
while (m -- )
{
int a, b, c;
cin >> a >> b >> c;
g[a][b] = g[b][a] = min(g[a][b], c);
}
int res = INF;
memcpy(d, g, sizeof g);
for (int k = 1; k <= n; k ++ )
{
for (int i = 1; i < k; i ++ )
for (int j = i + 1; j < k; j ++ )
if ((long long)d[i][j] + g[j][k] + g[k][i] < res)
{
res = d[i][j] + g[j][k] + g[k][i];
cnt = 0;
ans[cnt ++ ] = k;
ans[cnt ++ ] = i;
get_path(i, j);
ans[cnt ++ ] = j;//按环顺序输出
}
for (int i = 1; i <= n; i ++ )
for (int j = 1; j <= n; j ++ )
if (d[i][j] > d[i][k] + d[k][j])
{
d[i][j] = d[i][k] + d[k][j];
pre[i][j] = k;
}
}
if (res == INF) puts("No solution.");
else
{
for (int i = 0; i < cnt; i ++ ) cout << ans[i] << ' ';
cout << endl;
}
return 0;
}
dijkstra求最小环
有向图的最小环用Dijkstra求的时候也可以从1到n枚举s,用dij求解s的单元最短路径,把与s相连的点更新之后,再把d[s]设成inf,这样当s再一次被取出的时候,d[s]就是经过s的最小环长度,这样做是O(n*mlogn)的.
例题
acwing1128
对于每个点来说,它第一次收到信的时间等于到起点的最短距离,求所有节点到起点的最短距离,取最大值即可
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 110, INF = 0x3f3f3f3f;
int n, m;
int d[N][N];
int main()
{
cin >> n >> m;
memset(d, 0x3f, sizeof d);
for (int i = 0; i < m; i ++ )
{
int a, b, c;
cin >> a >> b >> c;
d[a][b] = d[b][a] = min(d[a][b], c);
}
for (int k = 1; k <= n; k ++ )
for (int i = 1; i <= n; i ++ )
for (int j = 1; j <= n; j ++ )
d[i][j] = min(d[i][j], d[i][k] + d[k][j]);
int res = 0;
for (int i = 1; i <= n; i ++ )
if (d[1][i] == INF)
{
res = -1;
break;
}
else res = max(res, d[1][i]);
cout << res << endl;
return 0;
}
2.Dijkstra/spfa
题解
分别枚举每个起点,求其他点到起点的距离之和,取最小值。
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 810, M = 3000, INF = 0x3f3f3f3f;
int n, p, m;
int id[N];
int h[N], e[M], w[M], ne[M], idx;
int dist[N], q[N];
bool st[N];
void add(int a, int b, int c)
{
e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++ ;
}
int spfa(int start)
{
memset(dist, 0x3f, sizeof dist);
dist[start] = 0;
int hh = 0, tt = 1;
q[0] = start, st[start] = true;
while (hh != tt)
{
int t = q[hh ++ ];
if (hh == N) hh = 0;
st[t] = false;
for (int i = h[t]; ~i; i = ne[i])
{
int j = e[i];
if (dist[j] > dist[t] + w[i])
{
dist[j] = dist[t] + w[i];
if (!st[j])
{
q[tt ++ ] = j;
if (tt == N) tt = 0;
st[j] = true;
}
}
}
}
int res=0;
for(int i=0;i<n;i++)
{
int j=id[i];
if(dist[j] == INF)
return INF;
res+=dist[j];
}
return res;
}
int main()
{
cin >> n >> p >> m;
for (int i = 0; i < n; i ++ ) cin >> id[i];
memset(h, -1, sizeof h);
for (int i = 0; i < m; i ++ )
{
int a, b, c;
cin >> a >> b >> c;
add(a, b, c), add(b, a, c);
}
int res = INF;
for (int i = 1; i <= p; i ++ )
res = min(res, spfa(i));
cout<<res<<endl;
return 0;
}
题解
设当前从A走到B的路径为$w_1,w_2,....,w_k$
z%表示转账的手续费,则$w_i$ =1-z表示x与y之间的汇率,要求终点的钱数为100,则满足$Aw_1w_2....w_k$=100,要求
A最小,则$w_1w_2....w_k$最大,取log,$logw_1+logw_2+…+logw_i$最大,由于0<w<1,则要求-($-logw_1-logw_2-…-logw_i$)最小,且括号每一项都大于0,即求括号里和的最小值(起点到终点最短路)。
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 2010;
int n, m, S, T;
double g[N][N];//g初始化为0,0两个点表示不连通
double dist[N];//求最大值,初始化为0
bool st[N];
void dijkstra()
{
dist[S] = 1;
for (int i = 1; i <= n; i ++ )
{
int t = -1;
for (int j = 1; j <= n; j ++ )
if (!st[j] && (t == -1 || dist[t] < dist[j]))
t = j;
st[t] = true;
for (int j = 1; j <= n; j ++ )
dist[j] = max(dist[j], dist[t] * g[t][j]);
}
}
int main()
{
scanf("%d%d", &n, &m);
while (m -- )
{
int a, b, c;
scanf("%d%d%d", &a, &b, &c);
double z = (100.0 - c) / 100;
g[a][b] = g[b][a] = max(g[a][b], z);
}
cin >> S >> T;
dijkstra();
printf("%.8lf\n", 100 / dist[T]);
return 0;
}
求乘积最大(即w1w2....wk最大)路径时,0[HTML_REMOVED]1才能用dijkstra
若只给了w>0,只只能用spfa(相当于有负权边)
(依据都是转成log式子等价成最短路)
acwing902
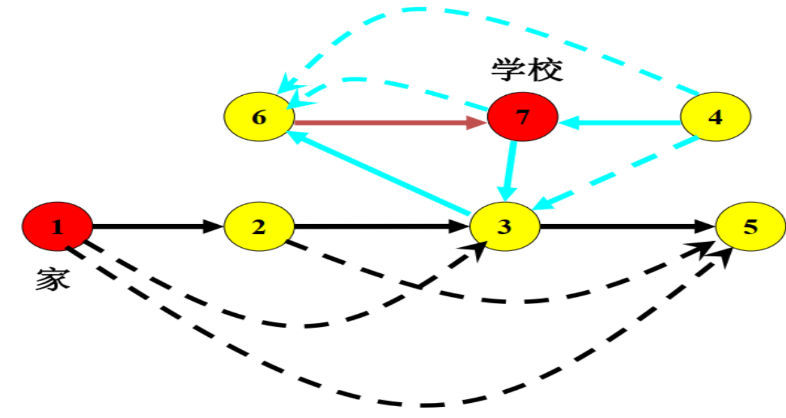
我们把同一条线路上的所有车站之间全部连一条边,这样就可以直接利用bfs求得最短距离,因为bfs只要到达终点就一定是最短的。
#include<iostream>
#include<sstream>
#include<cstring>
using namespace std;
const int N=510,INF=0x3f3f3f3f;
bool g[N][N];
int dist[N];
int n,m;
int stop[N];
int q[N];
int hh,tt;
int bfs()
{
memset(dist,0x3f,sizeof dist);
dist[1]=0;
q[0]=1;
while(hh <= tt)
{
int t=q[hh++];
if(t == n)
return dist[n];
for(int i=1;i<=n;i++)
if(g[t][i] && dist[i] > dist[t] + 1)
{
dist[i]=dist[t]+1;
q[++tt]=i;
}
}
return -1;
}
int main()
{
cin>>m>>n;
getchar();
for(int i=0;i<m;i++)
{
string line;
getline(cin,line);
stringstream ss(line);
int cnt=0,p;
while(ss>>p)
stop[cnt++]=p;
// cout<<i+1<<" :"<<endl;
// for(int i=0;i<cnt;i++)
// cout<<stop[i]<<' ';
// cout<<endl;
for(int j=0;j<cnt;j++)
for(int k=j+1;k<cnt;k++)
g[stop[j]][stop[k]]=true;
}
int t=bfs();
if(t==-1)
puts("NO");
else
cout<<max(dist[n]-1,0)<<endl;//起点和终点重合,换乘次数为0
return 0;
}
acwing903
(1)建立一个超级源点0,从0建立一条边到每个物品,权值为物品的价值。代表花费多少钱就可以直接购买这个物品。
(2)若某个物品拥有替代品,代表从替代品建立一条边到这个物品,价值为替代的价值。 代表我有了这个替代品,那么还需要花费多少就能买这个物品。
(3)最后就是等级制度。我们可以枚举每个等级区间,每次求最短路是只能更新在这个区间里面的物品。枚举所有情况求一个最小值就可以了。 特别注意的是区间必须包含1点。 那么范围就是[level[1] - m, level[1]]
#include<iostream>
#include<cstring>
using namespace std;
const int N=110,INF=0x3f3f3f3f;
int g[N][N];
int level[N];
int n,m;
bool st[N];
int dist[N];
int dijkstra(int down,int up)
{
memset(dist,0x3f,sizeof dist);
memset(st,false,sizeof st);
dist[0]=0;
for(int i=0;i<n+1;i++)
{
int t=-1;
for(int j=0;j<=n;j++)
if(!st[j] && (t==-1 || dist[j] < dist[t]))
t=j;
st[t]=true;
for (int j = 1; j <= n; j ++ )
if (level[j] >= down && level[j] <= up )
dist[j] = min(dist[j], dist[t] + g[t][j]);
}
return dist[1];
}
int main()
{
cin>>m>>n;
memset(g,0x3f,sizeof g);
for(int i=1;i<=n;i++)
{
int price,cnt;
cin>>price>>level[i]>>cnt;
g[0][i]=min(g[0][i],price);
while(cnt--)
{
int id,cost;
cin>>id>>cost;
g[id][i]=min(g[id][i],cost);
}
}
int res=INF;
for(int i=level[1]-m;i<=level[1];i++)
res=min(res,dijkstra(i,i+m));
cout<<res<<endl;
return 0;
}
#include<iostream>
#include<cstring>
#include<queue>
using namespace std;
const int maxn=1005,maxe=1000001;
const int inf=0x3f3f3f3f;
int T,n,m,w,cnt;
int head[maxn],dis[maxn];
bool vis[maxn];//标记是否已访问
struct node
{
int to,next,c;
}e[maxe];
void add(int u,int v,int cc)
{
e[++cnt].to=v;
e[cnt].next=head[u];
head[u]=cnt;
e[cnt].c=cc;
}
void dijkstra(int u)
{
priority_queue<pair<int,int> >q;
memset(vis,0,sizeof(vis));
memset(dis,0,sizeof(dis));
dis[u]=inf;
q.push(make_pair(dis[u],u));//最大值优先
while(!q.empty())
{
int x=q.top().second;
q.pop();
if(vis[x])
continue;
vis[x]=1;
if(vis[n])
return;
for(int i=head[x];i;i=e[i].next)
{
int v=e[i].to;
if(vis[v])
continue;
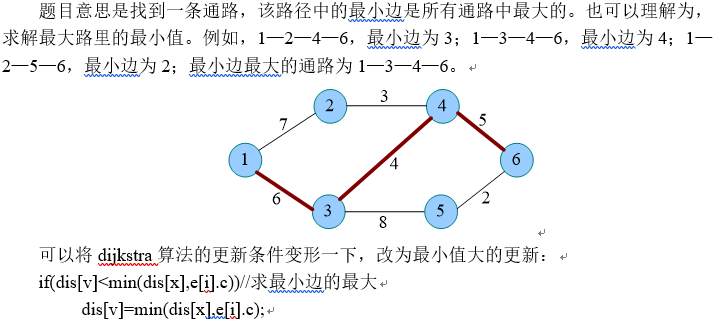
if(dis[v]<min(dis[x],e[i].c))//最小边是所有通路里最大的
{
dis[v]=min(dis[x],e[i].c);
q.push(make_pair(dis[v],v));
//cout<<v<<" "<<dis[v]<<endl;
}
}
}
}
int main()
{
int p=1;
cin>>T;
while(T--)
{
cnt=0;
memset(head,0,sizeof(head));
cin>>n>>m;
int u,v,t;
for(int i=1;i<=m;i++)
{
cin>>u>>v>>t;
add(u,v,t);//两条边
add(v,u,t);
}
dijkstra(1);
cout<<"Scenario #"<<p++<<":"<<endl;
cout<<dis[n]<<endl<<endl;
}
return 0;
}
也可用最大生成树求解
#include<cstdio>
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N=1010,M = 1e6+5,INF=0x3f3f3f3f;
struct Node
{
int x,y,val;
bool operator<(const Node& a)const
{
return val > a.val;
}
}G[M];
int p[N];
int Find(int x)
{
if(x != p[x])
p[x]=Find(p[x]);
return p[x];
}
int main()
{
int T = 0;
int Case = 1;
scanf("%d",&T);
while(T--)
{
int n,m;
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)
p[i] = i;
for(int i=0;i<m;i++){
scanf("%d%d%d",&G[i].x,&G[i].y,&G[i].val);
}
sort(G,G+m);
int ans = INF;
for(int i=0;i<m;i++){
int t1 = Find(G[i].x);
int t2 = Find(G[i].y);
if(t1!=t2){
p[t2] = t1;
if(Find(1)==Find(n)){ //最先找到让1和n连通的路径就是答案
ans = G[i].val;
break;
}
}
}
printf("Scenario #%d:\n",Case++);
printf("%d\n\n",ans);
}
return 0;
}
poj2253
要求所有通路里最大边最小
这道题应作为图论题,而不是最短路题,虽然有着相似之处吧,就像prim算法和最短路也是相似的,他们都有着一个特点,含有一个d[]数组,代表着不同的含义,最短路里代表从起始点到达当前点的最最路径,而prim算法里的则代表把当前点连入到已经连好的部分图形中的最小距离。而这个题中数组则代表从起始点到达当前点的最小跳远距离(那一条路径里最大的边),然后,维护d数组就可以了。
#include<cmath>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<iostream>
#define x first
#define y second
#define INF 0x3f3f3f3f
using namespace std;
const int N=210;
double w[N][N];
double dist[N];
bool st[N];
int n;
typedef pair<double ,double> PDD;
PDD p[N];
void djskstra()
{
for(int i=1;i<=n;i++)
dist[i]=INF;
memset(st,0,sizeof st);
dist[1]=0;
for(int i=1; i<=n; i++)
{
int t=-1;
for(int j=1; j<=n; j++)
if(!st[j]&&(t == -1 || dist[t] > dist[j] ))
t=j;
st[t]=true;
for(int j=1;j<=n;j++)
if(dist[j] > max(dist[t],w[t][j]))
dist[j]=max(dist[t],w[t][j]);
}
}
double get_path(int i,int j)
{
double x=p[i].x-p[j].x;
double y=p[i].y-p[j].y;
return sqrt(x*x+y*y);
}
int main()
{
int t=1;
while(scanf("%d",&n)&&n)
{
for(int i=1; i<=n; i++)
scanf("%lf%lf",&p[i].x,&p[i].y);
for(int i=1; i<=n; i++)
for(int j=i; j<=n; j++)
w[i][j]=w[j][i]=get_path(i,j);
djskstra();
printf("Scenario #%d\nFrog Distance = %.3f\n\n",t++,dist[2]);//注意格式
}
}
最短路+暴搜
acwing1135
五个点加上起点总共6个点,第一个点是1,固定的,其它点顺序任意,不好一遍处理完;但是总共才6个点,所以可以想到每个点来一次单源最短路,分别用一个dist数组记录;然后就是枚举所有可能的排列,求最小的路径即可
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
#include <queue>
using namespace std;
typedef pair<int, int> PII;
const int N = 50010, M = 200010, INF = 0x3f3f3f3f;
int n, m;
int h[N], e[M], w[M], ne[M], idx;
int q[N], dist[7][N];
int source[6];
bool st[N];
void add(int a, int b, int c)
{
e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++ ;
}
void dijkstra(int start, int dist[])
{
memset(dist, 0x3f, N * 4);
dist[start] = 0;
memset(st, 0, sizeof st);
priority_queue<PII, vector<PII>, greater<PII>> heap;
heap.push({0, start});
while (heap.size())
{
auto t = heap.top();
heap.pop();
int ver = t.second;
if (st[ver]) continue;
st[ver] = true;
for (int i = h[ver]; ~i; i = ne[i])
{
int j = e[i];
if (dist[j] > dist[ver] + w[i])
{
dist[j] = dist[ver] + w[i];
heap.push({dist[j], j});
}
}
}
}
int dfs(int u, int cnt, int distance)
{
if (cnt == 5) return distance;
int res = INF;
for (int i = 2; i <= 6; i ++ )
if (!st[i])
{
int next = source[i];
st[i] = true;
res = min(res, dfs(i, cnt+1, distance + dist[u][next]));
st[i] = false;
}
return res;
}
int main()
{
scanf("%d%d", &n, &m);
source[1] = 1;
for (int i = 2; i <= 6; i ++ ) scanf("%d", &source[i]);
memset(h, -1, sizeof h);
while (m -- )
{
int a, b, c;
scanf("%d%d%d", &a, &b, &c);
add(a, b, c), add(b, a, c);
}
for (int i = 1; i <= 6; i ++ ) dijkstra(source[i], dist[i]);
memset(st, 0, sizeof st);
printf("%d\n", dfs(1, 0, 0));
return 0;
}
枚举所有可能的排列也可以用状压dp,参考墨染空大佬代码
状态表示:f[S][j] :当前走到弟j号亲戚,已走过的路径方案为S
状态转移:
枚举已走过的k号亲戚
则f[S | 1<<j][j]=min(f[S| 1<<j],f[S][k]+dist[k][j]);
边界: f[1<<j][j]=dist[0][j];//从起点到各个亲戚家的最短距离
f[(1<<5)-1][j]表示终点为j的方案,取所有方案最小值res
dijkstra(1,dist[0]);
for (int i = 1; i < 6; i ++ )
{
dijkstra(source[i], dist[i]);
f[1 << (i - 1)][i - 1] = dist[0][source[i]];
}
for (int i = 0; i < (1 << 5); i++)
for (int j = 0; j < 5; j++)
{
if(i >> j & 1) continue;
for (int k = 0; k < 5; k++)
if(i >> k & 1)
f[i | (1 << j)][j] = min(f[i | (1 << j)][j], f[i][k] + dist[k + 1][source[j + 1]]);
}
int res = INF;
for (int i = 0; i < 5; i++) res = min(res, f[(1 << 5) - 1][i]);
printf("%d\n", res);
最短路+二分
acwing340
(1)我们需要求1 ~ N这条路径上的第k + 1大的值,前面k条作为免费升级,那么总结下来就是求所有1到N的路径上的第k + 1大的值中的最小值//所有1到N的路径,每条路径的k + 1大的值,然后这些k + 1大的值选取最小的作为答案输出
(2)求最大值的最小值,我们可以使用二分,二分出来的是满足在1 ~ N这条路径上,大于x的边小于等于k条的最小值,即不仅要满足x最小,同时也要满足性质(大于x的边小于等于k条,这样路径上才不会超过k条电缆),那么这个二分的区间的边从小到大排列,从0 ~ 1e6 + 1。(答案是有可能等于0的,即路径长度小于k,那么所有都可以升级为免费服务,1e6 + 1的原因是,如果二分如果找不到答案的话,会一直往右边区间靠(即l = mid + 1),直到右端点,那么边的权重上限是1e6,我们无法判断这个1e6是否是满足性质的,那么就需要1e6 + 1,作为无解的情况.)
(3)性质是大于这个检查点的边的条数<=k这个,那么我们需要求出从1 ~ N这条路径上大于这个检查点的边的条数<=k,最短路的目的是那么我们将大于检查点的边的权重看成1,小于等于检查点的权看为为0,求出从1号点到每个点的最短距离,那么从1号点到N号点的最短路是最少有几条大于检查点的条数,如果这个条数小于等于k,就满足性质,否则,如果这个最小条数都大于k,就不满足性质,然后我们就缩小这个检查值.
#include<iostream>
#include<cstring>
#include<deque>
using namespace std;
const int N=1010,M=20010;
int n,m,k;
int h[N],e[M],ne[M],w[M],idx;
int dist[N];
deque<int> q;
bool st[N];
void add(int a, int b, int c)
{
e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++ ;
}
bool check(int mid)
{
memset(dist,0x3f,sizeof dist);
memset(st,0,sizeof st);
q.push_back(1);
dist[1]=0;
while(q.size())
{
int t=q.front();
q.pop_front();
if(st[t])
continue;
st[t]=true;
for(int i=h[t];~i;i=ne[i])
{
int j=e[i],x=w[i]>mid;
if(dist[j] > dist[t] + x)
{
dist[j]=dist[t]+x;
if(!x)
q.push_front(j);
else
q.push_back(j);
}
}
}
if(dist[n] <= k)
return true;
else
return false;
}
int main()
{
cin>>n>>m>>k;
memset(h,-1,sizeof h);
while(m--)
{
int a,b,c;
cin>>a>>b>>c;
add(a,b,c);
add(b,a,c);
}
int l=0,r=1e6+1;
while(l<r)
{
int mid=l+r>>1;
if(check(mid))
r=mid;
else
l=mid+1;
}
if(r == 1e6+1)
cout<<-1<<endl;
else
cout<<l<<endl;
return 0;
}
分层图解法
#include <iostream>
#include<queue>
#include<cstring>
#include<cstdio>
using namespace std;
int n, m, k;
const int N=110010,M=2200010,INF=0x3f3f3f3f;
int h[N],e[M],ne[M],w[M],idx;
typedef pair<int,int> PII;
int dis[N];
bool vis[N];
void add(int a,int b,int c)
{
e[idx]=b;
w[idx]=c;
ne[idx]=h[a];
h[a]=idx++;
}
void dijkstra()
{
priority_queue<PII,vector<PII>,greater<PII> > heap;
memset(dis,0x3f,sizeof(dis));
memset(vis,0,sizeof(vis));
dis[1]=0;
heap.push({dis[1],1});
while(!heap.empty())
{
int t = heap.top().second;
heap.pop();
if(vis[t]) continue;
vis[t] = true;
for(int i = h[t]; ~i; i = ne[i])
{
int j = e[i];
if(vis[j])
continue;
if(dis[j] > max(dis[t],w[i]))//最大边是所有通路里最小
{
dis[j] = max(dis[t],w[i]);
heap.push({dis[j],j});
}
}
}
}
int main()
{
scanf("%d%d%d", &n, &m, &k);
memset(h,-1,sizeof h);
while(m--)
{
int u, v, w;
scanf("%d%d%d",&u, &v, &w);
for(int i = 0; i <= k; i++)
{
add(u + i * n, v + i * n, w);
add(v + i * n, u + i * n, w);
if(i != k)
{
add(u + i * n, v + (i + 1) * n, 0);
add(v + i * n, u + (i + 1) * n, 0);
}
}
}
dijkstra();
int ans = INF;
for(int i = 0; i <= k; i++)
ans = min(ans, dis[n + i * n]);
if(ans != INF)
printf("%d\n",ans);
else
printf("-1\n");
}
最短路+DAG
acwing342

这里有个细节就是,对于不能到达且不能更新的点,要删去它们相应的出边,否则拓扑排序就不能正常执行。这也就是为什么一开始加入s所在块时,还要把其它入度为0的块也算进去的原因。
#include<iostream>
#include<cstring>
#include<vector>
#include<queue>
using namespace std;
const int N=25010,M=150010,INF=0x3f3f3f3f;
int h[N],e[M],ne[M],w[M],idx;
int n,m1,m2,S;
int id[N];
vector<int> block[N];
int din[N];
typedef pair<int,int> PII;
int dist[N];
bool st[N];
int bcnt;
queue<int> q;
void add(int a, int b, int c)
{
e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++ ;
}
void dfs(int u,int bid)
{
id[u]=bid;
block[bid].push_back(u);
for(int i=h[u];~i;i=ne[i])
{
int j=e[i];
if(!id[j])
{
dfs(j,bid);
}
}
}
void dijkstra(int bid)
{
priority_queue<PII,vector<PII>,greater<PII> > heap;
for(int i=0;i<block[bid].size();i++)
{
int j=block[bid][i];
//cout<<bid<<": "<<j<<' '<<dist[j]<<endl;
heap.push({dist[j],j});
}
while(heap.size())
{
PII t=heap.top();
heap.pop();
int ver=t.second;
if(st[ver])
continue;
st[ver]=true;
for(int i=h[ver];~i;i=ne[i])
{
int j=e[i];
if (id[j] != id[ver] && -- din[id[j]] == 0)//对于不能到达且不能更新的点,要删去它们相应的出边
q.push(id[j]);
if (dist[j] > dist[ver] + w[i])
{
dist[j] = dist[ver] + w[i];
if (id[j] == id[ver])
heap.push({dist[j], j});
}
}
}
}
void toposort()
{
memset(dist,0x3f,sizeof dist);
dist[S]=0;
for(int i=1;i<=bcnt;i++)
if(!din[i])
q.push(i);
while(q.size())
{
int t=q.front();
q.pop();
dijkstra(t);
}
}
int main()
{
cin>>n>>m1>>m2>>S;
memset(h,-1,sizeof h);
while(m1--)
{
int a,b,c;
scanf("%d%d%d",&a,&b,&c);
add(a,b,c);
add(b,a,c);
}
for(int i=1;i<=n;i++)
if(!id[i])
{
bcnt++;
dfs(i,bcnt);
}
// for(int i=1;i<=bcnt;i++)
// {
// cout<<i<<": ";
// for(auto t: block[i])
// cout<<t<<' ';
// cout<<endl;
// }
while(m2--)
{
int a,b,c;
scanf("%d%d%d",&a,&b,&c);
din[id[b]]++;
add(a,b,c);
}
toposort();
for(int i=1;i<=n;i++)
if(dist[i] > INF/2)
cout<<"NO PATH"<<endl;
else
cout<<dist[i]<<endl;
return 0;
}
判断连通性也可用并查集
#include<iostream>
#include<cstring>
#include<vector>
#include<queue>
using namespace std;
const int N=25010,M=150010,INF=0x3f3f3f3f;
int h[N],e[M],ne[M],w[M],idx;
int n,m1,m2,S;
vector<int> block[N];
int din[N];
typedef pair<int,int> PII;
int dist[N];
bool st[N];
queue<int> q;
int p[N];
int find(int x)
{
if(p[x] != x)
p[x]=find(p[x]);
return p[x];
}
void add(int a, int b, int c)
{
e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++ ;
}
void dijkstra(int bid)
{
priority_queue<PII,vector<PII>,greater<PII> > heap;
for(int i=0;i<block[bid].size();i++)
{
int j=block[bid][i];
heap.push({dist[j],j});
}
while(heap.size())
{
PII t=heap.top();
heap.pop();
int ver=t.second;
if(st[ver])
continue;
st[ver]=true;
for(int i=h[ver];~i;i=ne[i])
{
int j=e[i];
int pj=find(j);
if (bid != pj && -- din[pj] == 0)
q.push(pj);
if (dist[j] > dist[ver] + w[i])
{
dist[j] = dist[ver] + w[i];
if (pj == bid)
heap.push({dist[j], j});
}
}
}
}
void toposort()
{
memset(dist,0x3f,sizeof dist);
dist[S]=0;
for(int i=1;i<=n;i++)
{
int pi=find(i);
if(!din[pi] && block[i].size())//小优化,只将当前点所在的连通块根节点入队,防止重复点进队多次
q.push(pi);
}
while(q.size())
{
int t=q.front();
q.pop();
//cout<<"---"<<t<<endl;
dijkstra(t);
}
}
int main()
{
cin>>n>>m1>>m2>>S;
memset(h,-1,sizeof h);
for(int i=1;i<=n;i++)
p[i]=i;
while(m1--)
{
int a,b,c;
scanf("%d%d%d",&a,&b,&c);
add(a,b,c);
add(b,a,c);
int pa=find(a);
int pb=find(b);
p[pa]=pb;
}
for(int i=1;i<=n;i++)
block[find(i)].push_back(i);
while(m2--)
{
int a,b,c;
scanf("%d%d%d",&a,&b,&c);
int pb=find(b);
din[pb]++;
add(a,b,c);
}
toposort();
for(int i=1;i<=n;i++)
if(dist[i] > INF/2)
cout<<"NO PATH"<<endl;
else
cout<<dist[i]<<endl;
return 0;
}
总结 :缩点+DAG
我们在每个联通块中用dijkstra跑最短路,再采用缩点的思想,将每个联通块看成一个点,在加 入航线,组成有向无环图,在按照拓扑排序进行扫 描,可以在线性时间求出单源最短路。
最短路+dp
acwing341
状态:dp[i] : 表示在i点前(包含I点)买入,i点后(包含i点)卖出所能获得的最大收益。
状态划分:
dp[i]=max(dp[i],dmax[i]-dmin[i]),dmin表示从起点到i所有路径中价格最小的是多少,dmax表示从i到n所有路径中价格最大的是多少。
(1)阿龙沿着某条路径从1-n的过程中,一定是先买后卖,那么假设在u节点买,在v节点卖,一定是先经过u再经过v。那么最优的策略一定是在当前路径下寻找最小的u,最大的v。
那么最优策略就藏在dmax[i]-dmin[i]中了。如果dmax[i],dmin[i]被计算出来,那么只需遍历一遍就能求出最终答案了。
(2)那么假如点u到v,有 dmin[v]=min(dmin[u],,price[v]) 其中price是记录每个节点价格的数组。dmax[v]=max(dmax[u],price[v]);
回顾题面:
“阿龙决定从 1 号城市出发,并最终在 n 号城市结束自己的旅行。”
也就是说卖完后要回到点n,然而题目并没有保证从任意点出发能去到点n!
而且不是所有边都是无向边。所以我们要知道哪些点不能去到点n,
可以反向建图,在这张图以n为起点看能到达哪些点。
唯一不同点:计算dmin数组起点是原点,终点是i,而计算dmax数组起点是i终点是n。那么我们可以建一张反图,反向图,既然i能到n,那么在反图中,n也能到i,从而dmax数组要从n开始算起。(同时可以保证买入点一定在卖出点之前,相当于以i为分界点,将整个区间划分成[1,i],[i,n])。
求 dmin[i] 和 dmax[i] 时,由于不是拓扑图,状态的更新可能存在环,因此不能使用动态规划,只能使用求最短路的方式。
#include<iostream>
#include<cstring>
using namespace std;
const int N=100010,M=2000010;
int h[N],rh[N],e[M],ne[M],idx;
int price[N];
int n,m;
int dmin[N];
int dmax[N];
int q[N];
bool st[N];
int dp[N];
void add(int h[], int a, int b)
{
e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}
void spfa(int h[],int dist[],int type)
{
int hh=0,tt=1;
if(type == 0)
{
memset(dist,0x3f,sizeof dmin);
dist[1]=price[1];
q[0]=1;
}
else
{
memset(dist,-0x3f,sizeof dmax);
dist[n]=price[n];
q[0]=n;
}
while(hh != tt)
{
int t=q[hh++];
if(hh == N)
hh=0;
st[t]=false;
for(int i=h[t];~i;i=ne[i])
{
int j=e[i];
if(!type && dist[j] > min(dist[t],price[j]) || type && dist[j] < max(dist[t],price[j]))
{
if(!type)
dist[j]=min(dist[t],price[j]);
else
dist[j]=max(dist[t],price[j]);
if(!st[j])
{
q[tt++]=j;
if(tt == N)
tt=0;
st[j]=true;
}
}
}
}
}
int main()
{
scanf("%d%d",&n,&m);
memset(h,-1,sizeof h);
memset(rh,-1,sizeof rh);
for(int i=1;i<=n;i++)
scanf("%d",&price[i]);
while(m--)
{
int a,b,c;
scanf("%d%d%d",&a,&b,&c);
add(h,a,b),add(rh,b,a);
if(c == 2)
add(h,b,a),add(rh,a,b);
}
spfa(h,dmin,0);
spfa(rh,dmax,1);
for(int i=1;i<=n;i++)
dp[i]=max(dp[i],dmax[i]-dmin[i]);
int res=0;
for(int i=1;i<=n;i++)
res=max(res,dp[i]);
cout<<res<<endl;
return 0;
}
总结: spfa求点权最大/最小(dp)+反图
分层图解法
(1)你可以在图上任意走动
(2)最终答案只与你的买入与卖出价格有关(我们就把买入卖出价值作为边权)
(3)如果你买入了一个水晶球,你是没有不卖它的道理的(显然咯,买了不卖血亏…)
而此题的难点在与你如何知道你是否能够到达买入,卖出,终点,和你能否把所有可能的情况考虑在内。
分层图可以很好的解决这个问题。
- 由于可以任意走动,所以我们可以建一张图,令图上的边全都是0,表示我的走动对我最终的结果没有影响。
考虑某个点 i ,它买入或者卖出水晶球的花费是v[i] 。 - 那么当我们进行买入操作,我们就建立一条有向边转移到一张新图上,边的大小为-v[i],指向点i所能到达的点(在第二层图上)而这张新图就是我们的第二层图。
它表示:假如我选择走了这条边,就是我在这个点买了这个水晶球,我不会反悔,并且我接下来考虑在某个点卖它。 - 当我们进行卖出操作,我们建立一条有向边转移到第三层图上,边的大小为v[i],指向i所能到达的点(在第三层图上)。
它表示:假如我选择走了这条边,就是我在这个点卖了这个水晶球,我不会反悔,并且我接下来考虑走向终点。
可以发现,从第一层图走到第二层图走到第三层图走到终点,这就是一个合法的选择,而且分层图把所有可能的决策都考虑到了。
最后走向终点,我们有两种合法的操作:
* 不买卖直接走向终点
直接在第一层图的n号节点建立边权为0的有向边接入一个“超级终点”
* 买卖一次后走向终点
在第三层图的n号节点建立边权为0的有向边接入“超级终点”
最后解释一下为什么我们要分层:
因为当你分了层,你就可以从还未买入这个状态,转移到已经买入准备卖出这个状态,然后在转移到从卖出点走向终点的状态。由于有向边的建立,你不能从第二/三层走回第一层图,这保证了你只做一次买卖,而不是无限做买卖,符合了题目的要求
而我们最终的答案,就是求从第一层图的1号点,经过三层图走到“超级终点”的最长路,如图所示。
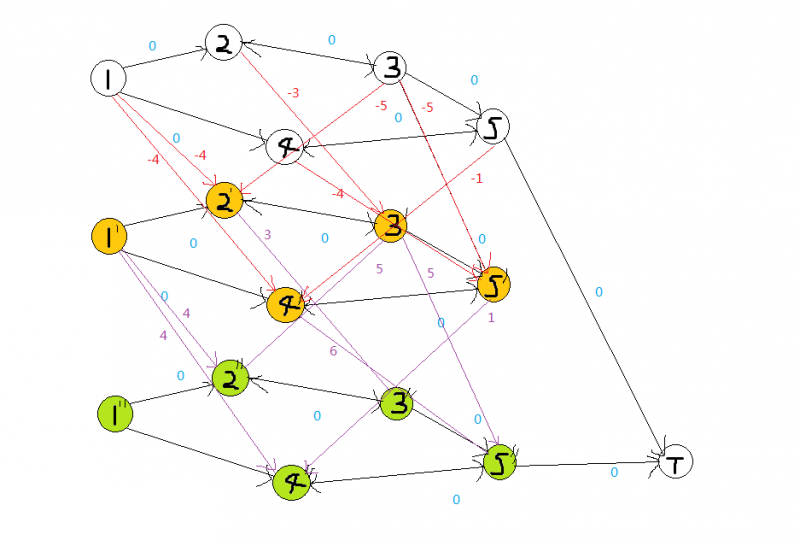
有负权,所以用 SPFA
#include<bits/stdc++.h>
using namespace std;
const int N=300010,M=50000010;
int h[N],e[M],ne[M],w[M],idx;
int q[N];
int dis[N],val[N];
bool v[N];
int n,m;
void add(int a,int b,int c)
{
e[idx]=b,w[idx]=c,ne[idx]=h[a],h[a]=idx++;
}
void spfa()
{
memset(dis,-0x3f,sizeof(dis));
memset(v,0,sizeof(v));
int hh=0,tt=1;
dis[1]=0;
v[1]=true;
q[0]=1;
while(hh != tt)
{
int x=q[hh++];
v[x]=0;
for(int i=h[x];~i;i=ne[i])
{
int j=e[i];
if(dis[j]<dis[x]+w[i])
{
dis[j]=dis[x]+w[i];
if(!v[j]) q[tt++]=j,v[j]=1;
}
}
}
}
int main()
{
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++) scanf("%d",&val[i]);
memset(h,-1,sizeof h);
for(int i=1,x,y,z;i<=m;i++)
{
scanf("%d%d%d",&x,&y,&z);
if(z==1)
{
add(x,y,0);
add(x,y+n,-val[x]);
//第一层
add(x+n,y+n,0);
add(x+n,y+2*n,val[x]);
//第二层
add(x+n*2,y+n*2,0);
//第三层
}
else
{
add(x,y,0); add(y,x,0);
add(x,y+n,-val[x]);add(y,x+n,-val[y]);
//第一层
add(x+n,y+n,0); add(y+n,x+n,0);
add(x+n,y+2*n,val[x]);add(y+n,x+2*n,val[y]);
//第二层
add(x+n*2,y+n*2,0); add(y+n*2,x+n*2,0);
//第三层
}
}
spfa();
if(dis[n*3]>0) printf("%d",dis[n*3]);
else printf("0");
return 0;
}
强连通分量解法(缩点+DAGdp)

也就是把状态分解成继承前面的状态(当前点不售出)和当前点售出,两者取较大值。
原图不一定为DAG,考虑使用tarjan缩点。
那么转移方程也得变成考虑一个连通分量的贡献。
这个最大利润可能出自同一个连通分量,也可能出自不同。

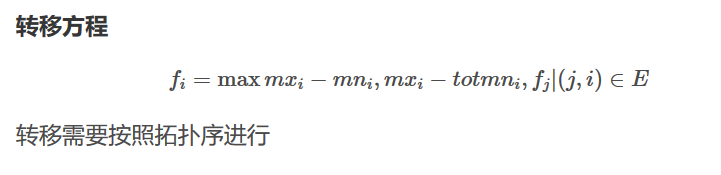
#include<iostream>
#include<cstring>
#include<cstdio>
#include<vector>
using namespace std;
const int N=100010,M=1000010,INF=0x3f3f3f3f;
int h[N],hs[N],e[M],ne[M],w[M],idx;
int n,m;
int id[N];
int p[N];
int minv[N],maxv[N],totmin[N],f[N];
int dfn[N], low[N], timestamp;
int stk[N], top;
bool ins[N];
int scc_cnt;
void add(int h[],int a, int b)
{
e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}
void tarjan(int u)
{
dfn[u]=low[u]=++timestamp;
stk[++top]=u,ins[u]=true;
for(int i=h[u];~i;i=ne[i])
{
int j=e[i];
if(!dfn[j])
{
tarjan(j);
low[u]=min(low[u],low[j]);
}
else if(ins[j])
low[u]=min(low[u],dfn[j]);
}
if(dfn[u] == low[u])
{
++scc_cnt;
minv[scc_cnt]=INF;
maxv[scc_cnt]=-INF;
int y;
do{
y=stk[top--];
ins[y]=false;
id[y]=scc_cnt;
minv[scc_cnt]=min(minv[scc_cnt],p[y]);
maxv[scc_cnt]=max(maxv[scc_cnt],p[y]);
}while(y != u);
}
}
int main()
{
// freopen("test.in.txt","r",stdin);
// freopen("test.out","w",stdout);
cin>>n>>m;
memset(h,-1,sizeof h);
memset(hs,-1,sizeof hs);
for(int i=1;i<=n;i++)
cin>>p[i];
while(m--)
{
int a,b,c;
scanf("%d%d%d",&a,&b,&c);
if(c == 1)
add(h,a,b);
else
add(h,a,b),add(h,b,a);
}
for(int i=1;i<=n;i++)
if(!dfn[i])
tarjan(i);
for(int i=1;i<=n;i++)
for(int j=h[i];~j;j=ne[j])
{
int k=e[j];
int a=id[i],b=id[k];
//cout<<a << ' '<<b<<endl;
if(a != b)
add(hs,a,b);
}
for(int i=scc_cnt;i;i--)
{
totmin[i]=minv[i];
}
for(int i=scc_cnt;i;i--)
{
for(int j=hs[i];~j;j=ne[j])
{
int k=e[j];
totmin[k]=min(totmin[k],minv[i]);
f[k]=max(max(f[k],f[i]),max(maxv[k]-minv[k],maxv[k]-totmin[k]));
//cout<<i<<' '<<k<<' '<<totmin[k]<<' '<<f[k]<<endl;
}
}
cout<<f[id[n]]<<endl;
return 0;
}
最短路的扩展
题解
求可以任选起点的情况下,到达任意一个终点的路径最小值。方法:建立虚拟源点。当然,本题也可在反图上从终点向起点跑最短路。
//可以任选起点的情况下,到达任意一个终点的路径最小值
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1010, M = 21010, INF = 0x3f3f3f3f;
int n, m, T;
int h[N], e[M], w[M], ne[M], idx;
int dist[N], q[N];
bool st[N];
void add(int a, int b, int c)
{
e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++ ;
}
int spfa()
{
memset(dist, 0x3f, sizeof dist);
int hh = 0, tt = 1;
q[0]=0;
dist[0]=0;
while (hh != tt)
{
int t = q[hh ++ ];
if (hh == N) hh = 0;
st[t] = false;
for (int i = h[t]; ~i; i = ne[i])
{
int j = e[i];
if (dist[j] > dist[t] + w[i])
{
dist[j] = dist[t] + w[i];
if (!st[j])
{
q[tt ++ ] = j;
if (tt == N) tt = 0;
st[j] = true;
}
}
}
}
}
int main()
{
while(~scanf("%d%d%d",&n,&m,&T))
{
memset(h, -1, sizeof h);
idx = 0;
while (m -- )
{
int a, b, c;
scanf("%d%d%d", &a, &b, &c);
add(a, b, c);
}
int p;
scanf("%d",&p);
while(p--)
{
int a;
scanf("%d",&a);
add(0,a,0);
}
spfa();
if(dist[T] == INF)
cout<<-1<<endl;
else
cout<<dist[T]<<endl;
}
return 0;
}
acwing1131

状态转移时有两种方式。填表法和刷表法。
填表法就是当前状态可由哪些自己转移过来。
刷表法就是当前的状态可以更新哪些状态。(最短路里的状态用刷表法较直观,和最短路模型更接近)
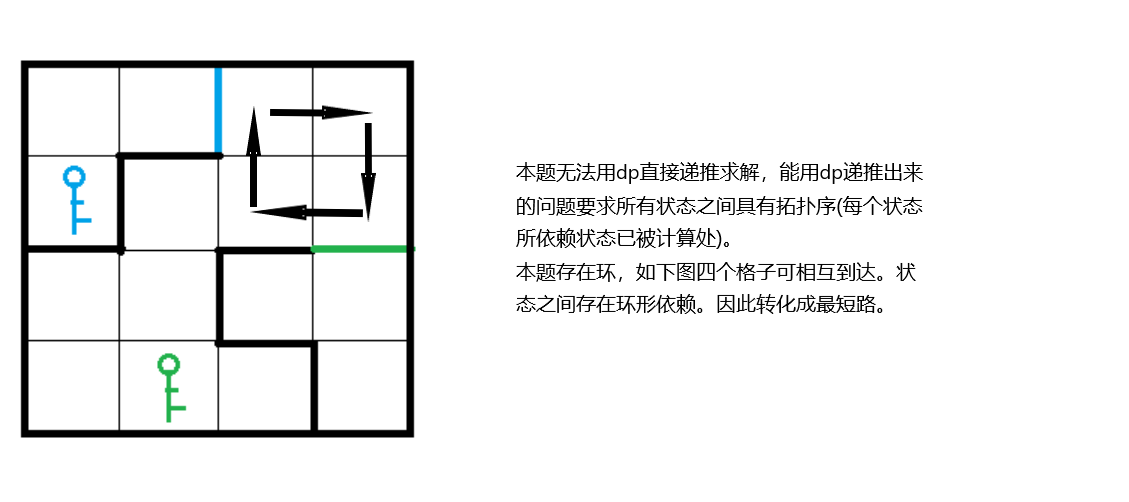
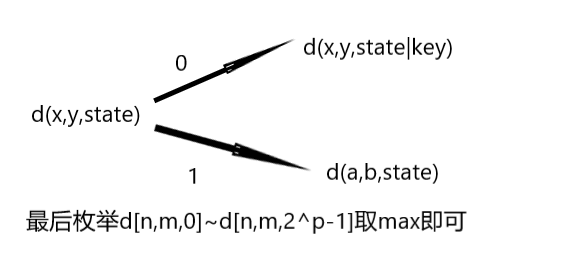
最短路->dp->最短路
#include<iostream>
#include<deque>
#include<cstring>
#include<set>
#define x first
#define y second
using namespace std;
const int N=11,M=N*N,E=400,P=1<<10;//边数2*2*n(n-1)
int n,m,k,p;
int h[M],e[E],ne[E],w[E],idx;
int g[N][N];
int dist[P][M];//dist[S][i]:走到i号点时钥匙的使用情况为S
bool st[P][M];
typedef pair<int,int> PII;
int dx[4]={-1,0,1,0},dy[4]={0,1,0,-1};
set<int> edges;
void add(int a, int b, int c)
{
e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++ ;
}
void build()
{
for(int i=0;i<n;i++)
for(int j=0;j<m;j++)
for(int k=0;k<4;k++)
{
int x=i+dx[k],y=j+dy[k];
if(x<0 || x>=n || y<0 || y>=m)
continue;
int a=i*m+j,b=x*m+y;
int hash1=a*100+b;
if(!edges.count(hash1))
add(a,b,0);//0表示无障碍
}
}
int bfs()
{
memset(dist,0x3f,sizeof dist);
dist[0][0]=0;//从0号点出发,所拥有钥匙状态为0
deque<PII> q;
q.push_back({0,0});
while(q.size())
{
PII t=q.front();
q.pop_front();
int x=t.y/m,y=t.y%m;
if (st[t.x][t.y])
continue;
st[t.x][t.y] = true;
if(t.y == n*m-1)
return dist[t.x][t.y];
if(g[x][y])//若该位置有钥匙,则将钥匙全部拿走
{
int state = t.x | g[x][y];
if(dist[state][t.y] > dist[t.x][t.y])
{
dist[state][t.y] = dist[t.x][t.y];
q.push_front({state, t.y});
}
}
for(int i=h[t.y];~i;i=ne[i])
{
int j=e[i];
if(w[i] && !(t.x>>w[i]-1 & 1))
continue;
if(dist[t.x][j] > dist[t.x][t.y] + 1)
{
dist[t.x][j] = dist[t.x][t.y] + 1;
q.push_back({t.x, j});
}
}
}
return -1;
}
int main()
{
cin>>n>>m>>p>>k;
memset(h,-1,sizeof h);
while(k--)
{
int x1,y1,x2,y2,c;
cin>>x1>>y1>>x2>>y2>>c;
int a=(x1-1)*m+y1-1,b=(x2-1)*m+y2-1;
int hash1=a*100+b,hash2=b*100+a;
edges.insert(hash1),edges.insert(hash2);
if(c)//c为0表示墙,不可逾越,不为0表示钥匙种类
add(a,b,c),add(b,a,c);
}
build();//建立剩下的可直达的边
int s;
cin>>s;
while(s--)
{
int a,b,id;
cin>>a>>b>>id;
g[a-1][b-1] |= 1<<id-1;
}
// for(int i=1;i<=n;i++)
// {
// for(int j=1;j<=m;j++)
// cout<<g[i][j]<<' ';
// cout<<endl;
// }
cout<<bfs()<<endl;
return 0;
}
acwing1134
最短路问题如何有拓扑序?
最短路树:记录每个点由哪个点更新得来的,得到一根树。(要求图上不存在权值和为0的环,一般求条数问题不存在长度为0的环)。
树天生具有拓扑序。
BFS 只入队一次,出队一次。可以抽象成拓扑图
dijkstra 每个点只出队一次。也可以抽象成拓扑图。
spfa 本身不具备拓扑序,但如果图中存在负权边只能用该算法做。先跑一般spfa,再检查每个边是否满足dist[j]=dist[t]+w[i],若满足说明该边存在于最短路树上。再在最短路树上做一般DAG dp即可。
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 100010, M = 400010, mod = 100003;
int n, m;
int h[N], e[M], ne[M], idx;
int dist[N], cnt[N];
int q[N];
void add(int a, int b)
{
e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}
void bfs()
{
memset(dist, 0x3f, sizeof dist);
dist[1] = 0;
cnt[1] = 1;
int hh = 0, tt = 0;
q[0] = 1;
while (hh <= tt)
{
int t = q[hh ++ ];
for (int i = h[t]; ~i; i = ne[i])
{
int j = e[i];
if (dist[j] > dist[t] + 1)
{
dist[j] = dist[t] + 1;
cnt[j] = cnt[t];
q[ ++ tt] = j;
}
else if (dist[j] == dist[t] + 1)
{
cnt[j] = (cnt[j] + cnt[t]) % mod;
}
}
}
}
int main()
{
scanf("%d%d", &n, &m);
memset(h, -1, sizeof h);
while (m -- )
{
int a, b;
scanf("%d%d", &a, &b);
add(a, b), add(b, a);
}
bfs();
for (int i = 1; i <= n; i ++ ) printf("%d\n", cnt[i]);
return 0;
}
acwing383
d[v][0]存最短路值,d[v][1]存次短路值
1.d[v][0]>minx+w 更新最短距离(但是记得更新次短距离,次短距离一定大于d[v][0],当d[v][0]更新成minx+w时,次短距离更新成原来的d[v][0])
2.d[v][0]==minx+w 找到相同最短距离,更新最短条数
3.d[v][1]>minx+w 更新次短距离
3.d[v][1]==minx+w 找到相同次短距离,更新次短条数
#include<iostream>
#include<cstring>
#include<queue>
using namespace std;
const int N=1010,M=100010;
int n, m, S, T;
int h[N], e[M], w[M], ne[M], idx;
int dist[N][2], cnt[N][2];
bool st[N][2];
struct Ver
{
int ver, type, dist;
bool operator> (const Ver &W) const
{
return dist > W.dist;
}
};
void add(int a, int b, int c)
{
e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++ ;
}
int dijkstra()
{
memset(st,0,sizeof st);
memset(dist,0x3f,sizeof dist);
memset(cnt,0,sizeof cnt);
dist[S][0]=0,cnt[S][0]=1;
priority_queue<Ver, vector<Ver>, greater<Ver>> heap;
heap.push({S,0,0});
while(heap.size())
{
Ver t=heap.top();
heap.pop();
int ver=t.ver,type=t.type,distance=t.dist,count=cnt[ver][type];
if(st[ver][type])
continue;
st[ver][type]=true;
for(int i=h[ver];~i;i=ne[i])
{
int j=e[i];
if(dist[j][0] > distance + w[i])
{
dist[j][1] = dist[j][0],cnt[j][1]=cnt[j][0];
heap.push({j,1,dist[j][1]});
dist[j][0]=distance + w[i],cnt[j][0]=count;
heap.push({j,0,dist[j][0]});
}
else if(dist[j][0] == distance + w[i])
cnt[j][0] += count;
else if (dist[j][1] > distance + w[i])
{
dist[j][1] = distance + w[i], cnt[j][1] = count;
heap.push({j,1,dist[j][1]});
}
else if (dist[j][1] == distance + w[i])
cnt[j][1] += count;
}
}
int res=cnt[T][0];
if (dist[T][0] + 1 == dist[T][1])
res += cnt[T][1];
return res;
}
int main()
{
int T;
cin>>T;
while(T--)
{
scanf("%d%d",&n,&m);
memset(h,-1,sizeof h);
idx=0;
while(m--)
{
int a,b,c;
scanf("%d%d%d",&a,&b,&c);
add(a,b,c);
}
scanf("%d%d",&S,&T);
printf("%d\n",dijkstra());
}
return 0;
}
分层图
分层图最短路是指在可以进行分层图的图上解决最短路问题。分层图:可以理解为有多个平行的图。
一般模型是:在一个正常的图上可以进行 k次决策,对于每次决策,不影响图的结构,只影响目前的状态或代价。一般将决策前的状态和决策后的状态之间连接一条权值为决策代价的边,表示付出该代价后就可以转换状态了。
一般有两种方法解决分层图最短路问题:
(1)建图时直接建成k+1层。
(2)多开一维记录机会信息。
第一种方法:
我们建k+1层图。然后有边的两个点,多建一条到下一层边权为0的单向边,如果走了这条边就表示用了一次机会。
有N个点时,1~n表示第一层,(n+1)~(n+n)代表第二层,(1+2n)~(n+2n)代表第三层,(1+i*n)~(n+i*n)代表第i+1层。因为要建K+1层图,数组要开到n * ( k + 1),点的个数也为n * ( k + 1 ) 。
对于数据:
n = 4,m = 3, k = 2
0 1 100
1 2 100
2 3 100
建成图之后大概是这样的:
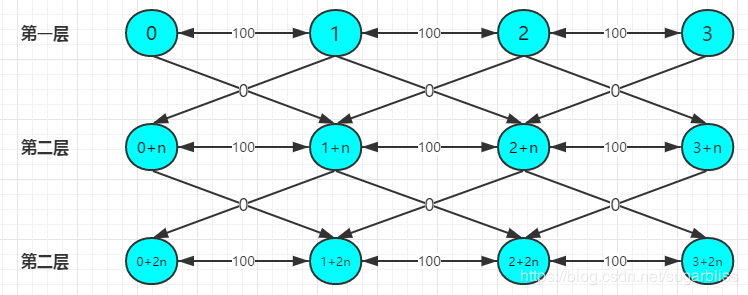
对于上面的数据:答案就是3,3+n,3+2n,中的最小值。
第一种模板:
#include <iostream>
#include<queue>
#include<cstring>
#include<cstdio>
using namespace std;
int n, m, s, t, k;
const int N=110010,M=2200010,INF=0x3f3f3f3f;
int h[N],e[M],ne[M],w[M],idx;
typedef pair<int,int> PII;
int dis[N];
bool vis[N];
void add(int a,int b,int c)
{
e[idx]=b;
w[idx]=c;
ne[idx]=h[a];
h[a]=idx++;
}
void dijkstra()
{
priority_queue<PII,vector<PII>,greater<PII> > heap;
memset(dis,0x3f,sizeof(dis));
memset(vis,0,sizeof(vis));
dis[s]=0;
heap.push({dis[s],s});
while(!heap.empty())
{
int t = heap.top().second;
heap.pop();
if(vis[t]) continue;
vis[t] = true;
for(int i = h[t]; ~i; i = ne[i])
{
int j = e[i];
if(vis[j])
continue;
if(dis[j] > dis[t] + w[i])
{
dis[j] = dis[t] + w[i];
heap.push({dis[j],j});
}
}
}
}
int main()
{
scanf("%d%d%d", &n, &m, &k);
scanf("%d%d",&s,&t);
memset(h,-1,sizeof h);
while(m--)
{
int u, v, w;
scanf("%d%d%d",&u, &v, &w);
for(int i = 0; i <= k; i++)
{
add(u + i * n, v + i * n, w);
add(v + i * n, u + i * n, w);
if(i != k)
{
add(u + i * n, v + (i + 1) * n, 0);
add(v + i * n, u + (i + 1) * n, 0);
}
}
}
dijkstra();
int ans = INF;
for(int i = 0; i <= k; i++)
ans = min(ans, dis[t + i * n]);
printf("%d\n",ans);
}
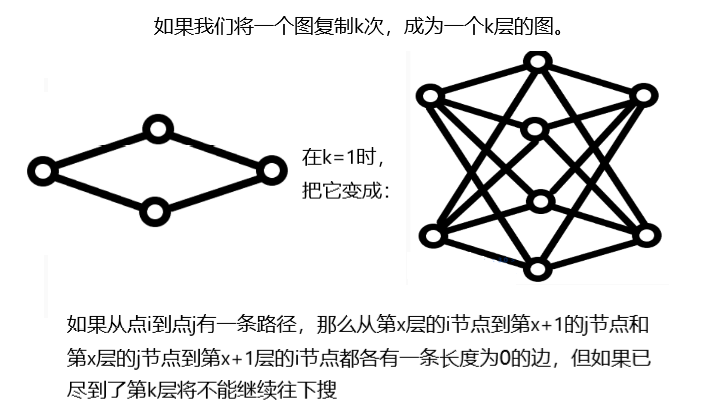
这是一道很经典的分层图最短路题
考虑把图分成 k层(就是每个点复制 k 次),第 i 层表示当前已经使用了 i 次免费机会。图片转自 銘权 大佬题解。

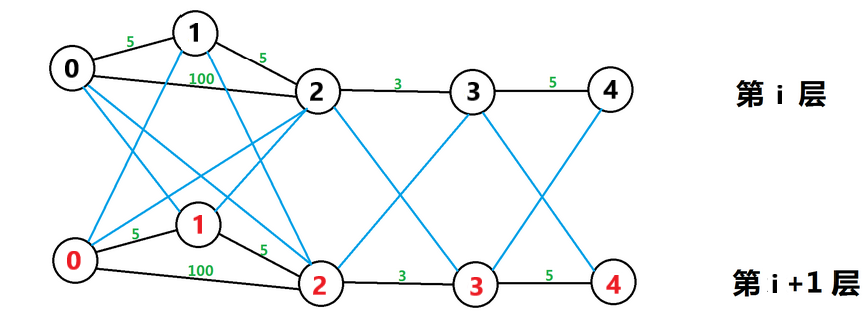
蓝边就是零边
总结:
分层图最短路就可以有效解决这种带有 「阶段性」的最短路。
我们把整个图分成k+1层(0∼k),第i+1层表示已经将i条道路免费的图,也就是说,每一层的道路和普通的最短路没有什么区别,只是多了一些从第i层到第i+1层的道路。这些道路的权值为0,这样就有效解决了免费的情况,因为如果最短路跑到了第k+1层说明使k条道路免费了。最终把每一层的终点连向一个超级汇点,权值为0,最短路就是第0层源点到超级汇点的最短路。
第二种方法:
我们把dis数组和vis数组多开一维记录k次机会的信息。
(1) dis[ i ][ j ] 代表到达 i 用了 j 次免费机会的最小花费.
(2) vis[ i ][ j ] 代表到达 i 用了 j 次免费机会的情况是否出现过.
更新的时候先更新同层之间(即花费免费机会相同)的最短路,然后更新从该层到下一层(即再花费一次免费机会)的最短路。
(1)不使用机会 dis[v][c] = min(dis[v][c],dis[u][c] + w(u,v));
(2) 使用机会 dis[v][c+1] = min(dis[v][c+1],dis[u][c]);
第二种模板
#include <iostream>
#include<queue>
#include<cstring>
#include<cstdio>
using namespace std;
int n, m, s, t, k;
const int N=110010,M=2100010,INF=0x3f3f3f3f;
int h[N],e[M],ne[M],w[M],idx;
typedef pair<int,int> PII;
int dis[N][15];
bool vis[N][15];
void add(int a,int b,int c)
{
e[idx]=b;
w[idx]=c;
ne[idx]=h[a];
h[a]=idx++;
}
void dijkstra()
{
// dis[ i ][ j ] 代表到达 i 用了 j 次免费机会的最小花费.
// vis[ i ][ j ] 代表到达 i 用了 j 次免费机会的情况是否出现过.
priority_queue<PII,vector<PII>,greater<PII> > heap;
memset(dis,0x3f,sizeof(dis));
memset(vis,0,sizeof(vis));
dis[s][0]=0;
heap.push({0,s});
while(!heap.empty())
{
int t = heap.top().second;
int c=t/n;//层数
t%=n;//当前层节点
heap.pop();
if(vis[t][c]) continue;
vis[t][c] = true;
for(int i = h[t]; ~i; i = ne[i])
{
int j = e[i];
if(vis[j][c])
continue;
if(dis[j][c] > dis[t][c] + w[i])
{
dis[j][c] = dis[t][c] + w[i];
heap.push({dis[j][c],j+c*n});
}
if(c<k)
{
if(dis[j][c+1] > dis[t][c])
{
dis[j][c+1] = dis[t][c];
heap.push({dis[j][c+1],j+(c+1)*n});
}
}
}
}
}
int main()
{
scanf("%d%d%d", &n, &m, &k);
scanf("%d%d",&s,&t);
memset(h,-1,sizeof h);
while(m--)
{
int u, v, w;
scanf("%d%d%d",&u, &v, &w);
for(int i = 0; i <= k; i++)
{
add(u , v, w);
add(v , u, w);
}
}
dijkstra();
int ans = INF;
for(int i = 0; i <= k; i++)
ans = min(ans, dis[t][i]);
printf("%d\n",ans);
}
推荐博客:
https://www.cnblogs.com/Yz81128/archive/2012/08/15/2640940.html
https://blog.csdn.net/ll365594480/article/details/6792096
https://www.cnblogs.com/GumpYan/p/5540549.html




收了,感谢巨巨