最小生成树性质

prim
模板题acwing1140
#include<iostream>
#include<cstring>
using namespace std;
const int N=110;
int g[N][N];
int n;
int dist[N];
bool st[N];
int prim()
{
int res=0;
memset(dist,0x3f,sizeof dist);
dist[1]=0;
for(int i=0;i<n;i++)
{
int t=-1;
for(int j=1;j<=n;j++)
if(!st[j] && (t==-1 || dist[t] > dist[j]))
t=j;
res+=dist[t];
st[t]=true;
for(int j=1;j<=n;j++)
dist[j]=min(dist[j],g[t][j]);
}
return res;
}
int main()
{
cin>>n;
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
cin>>g[i][j];
cout<<prim()<<endl;
return 0;
}
hdu1102
将已经有路的两个村庄之间的距离处理为0,然后用prim算法即可。
#include<iostream>
#include<cstring>
using namespace std;
const int N=110;
int g[N][N];
int n,m;
int dist[N];
bool st[N];
int prim()
{
int res=0;
memset(dist,0x3f,sizeof dist);
memset(st,0,sizeof st);
dist[1]=0;
for(int i=0;i<n;i++)
{
int t=-1;
for(int j=1;j<=n;j++)
if(!st[j] && (t==-1 || dist[t] > dist[j]))
t=j;
res+=dist[t];
st[t]=true;
for(int j=1;j<=n;j++)
dist[j]=min(dist[j],g[t][j]);
}
return res;
}
int main()
{
while(~scanf("%d",&n))
{
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
cin>>g[i][j];
cin>>m;
while(m--)
{
int a,b;
cin>>a>>b;
g[a][b]=g[b][a]=0;
}
cout<<prim()<<endl;
}
return 0;
}
acwing1141
删除若干条边,使得剩下的点两两联通,且删除的边的边权和最大,输出这个最大值.
#include<iostream>
#include<algorithm>
using namespace std;
const int N=110,M=210;
int n,m;
struct Edge
{
int a,b,w;
bool operator<(const Edge &W) const
{
return w<W.w;
}
}e[M];
int p[N];
int find(int x)
{
if(p[x] != x)
p[x]=find(p[x]);
return p[x];
}
int main()
{
cin>>n>>m;
for(int i=1;i<=n;i++)
p[i]=i;
for(int i=0;i<m;i++)
{
int a,b,c;
cin>>a>>b>>c;
e[i]={a,b,c};
}
sort(e,e+m);
int res=0;
for(int i=0;i<m;i++)
{
int a=find(e[i].a),b=find(e[i].b),w=e[i].w;
if(a != b)
p[a]=b;
else
res+=w;
}
cout<<res<<endl;
return 0;
}
二分
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N=310,M=8010;
int h[N],e[M],ne[M],w[M],idx;
int n,m;
int p[N];
struct edge
{
int a,b,c;
bool operator<(const edge &W)const
{
return c<W.c;
}
}edges[M];
bool st[N];
void add(int a,int b,int c)
{
e[idx]=b;
w[idx]=c;
ne[idx]=h[a];
h[a]=idx++;
}
int find(int x)
{
if(p[x] != x)
p[x]=find(p[x]);
return p[x];
}
void dfs(int u,int x)
{
st[u]=true;
for(int i=h[u];~i;i=ne[i])
{
int j=e[i];
if(w[i] > x)
continue;
if(!st[j])
dfs(j,x);
}
}
bool check(int x)
{
for(int i=0;i<m;i++)
{
int a=edges[i].a,b=edges[i].b,c=edges[i].c;
if(c>x)
continue;
int pa=find(a);
int pa=find(b);
p[pa]=pb;
}
}
int main()
{
cin>>n>>m;
memset(h,-1,sizeof h);
for(int i=1;i<=n;i++)
p[i]=i;
for(int i=0;i<m;i++)
{
int a,b,c;
cin>>a>>b>>c;
add(a,b,c);
add(b,a,c);
edges[i]={a,b,c};
}
sort(edges,edges+m);
int l=0,r=m-1;
while(l<r)
{
int mid=l+r>>1;
if(check(edges[mid].c))
r=mid;
else
l=mid+1;
}
cout<<n-1<<' '<<edges[l].c<<endl;
return 0;
}
krustral
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 310, M = 10010;
int n, m;
struct Edge
{
int a, b, w;
bool operator< (const Edge &t) const
{
return w < t.w;
}
}e[M];
int p[N];
int find(int x)
{
if (p[x] != x) p[x] = find(p[x]);
return p[x];
}
int main()
{
cin >> n >> m;
for (int i = 1; i <= n; i ++ ) p[i] = i;
for (int i = 0; i < m; i ++ )
{
int a, b, w;
cin >> a >> b >> w;
e[i] = {a, b, w};
}
sort(e, e + m);
int res = 0;
for (int i = 0; i < m; i ++ )
{
int a = find(e[i].a), b = find(e[i].b), w = e[i].w;
if (a != b)
{
p[a] = b;
res = w;
}
}
cout << n - 1 << ' ' << res << endl;
return 0;
}
acwign1143
缩点+最小生成树

//缩点
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 2010, M = 10010;
int n, m;
struct Edge
{
int a, b, w;
bool operator< (const Edge &t) const
{
return w < t.w;
}
}e[M];
int p[N];
int find(int x)
{
if (p[x] != x) p[x] = find(p[x]);
return p[x];
}
int main()
{
cin >> n >> m;
for (int i = 1; i <= n; i ++ ) p[i] = i;
int res = 0, k = 0;
for (int i = 0; i < m; i ++ )
{
int t, a, b, w;
cin >> t >> a >> b >> w;
if (t == 1)
{
res += w;
p[find(a)] = find(b);
}
else e[k ++ ] = {a, b, w};
}
sort(e, e + k);
for (int i = 0; i < k; i ++ )
{
int a = find(e[i].a), b = find(e[i].b), w = e[i].w;
if (a != b)
{
p[a] = b;
res += w;
}
}
cout << res << endl;
return 0;
}
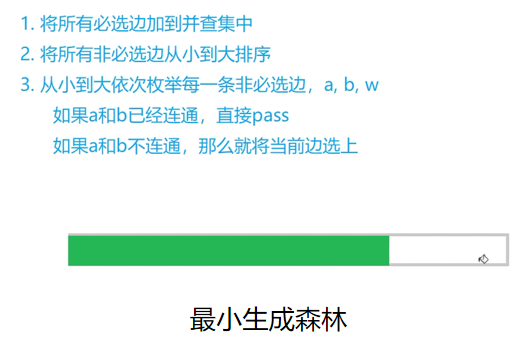
acwing1144
先枚举长度为1的边,在枚举长度为2的边,可省略一步排序。
已经选中的边也可放进边集舒数组,krustral执行到该边时会忽略该边。(该边所连的两点已在同一个连通块)
#include <cstdio>
#include <iostream>
using namespace std;
const int N = 1005;
int n, m, f[N * N], res = 0;
int get(int x)
{
return x == f[x] ? x : f[x] = get(f[x]);
}
// void get_edges()
// {
// int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1}, dw[4] = {1, 2, 1, 2};
// for (int z = 0; z < 2; z ++ )
// for (int i = 1; i <= n; i ++ )
// for (int j = 1; j <= m; j ++ )
// for (int u = 0; u < 4; u ++ )
// if (u % 2 == z)
// {
// int x = i + dx[u], y = j + dy[u], w = dw[u];
// if (x && x <= n && y && y <= m)
// {
// int a = ids[i][j], b = ids[x][y];
// if (a < b) e[k ++ ] = {a, b, w};
// }
// }
// }
int main()
{
scanf("%d%d", &n, &m);
for (int i = 1; i <= n * m; i++) f[i] = i;
int x1, y1, x2, y2;
while(~scanf("%d%d%d%d", &x1, &y1, &x2, &y2))
{
int a = (x1 - 1) * m + y1, b = (x2 - 1) * m + y2;
f[get(a)] = get(b);
}
for (int i = 1; i < n; i++)
{
for (int j = 1; j <= m; j++)
{
int a = (i - 1) * m + j, b = i * m + j;
a = get(a), b = get(b);
if(a != b) res++, f[a] = b;
}
}
for (int i = 1; i <= n; i++)
{
for (int j = 1; j < m; j++)
{
int a = (i - 1) * m + j, b = (i - 1) * m + j + 1;
a = get(a), b = get(b);
if(a != b) res += 2, f[a] = b;
}
}
printf("%d\n", res);
return 0;
}

acwing1146
为了供应电力,要么在当前位置 i 建发电站,要么与另外的已经有电力供应的矿井 j 之间建立电网
1、在当前位置i建发电站的费用是vi,建立虚拟结点S,相当于i号点到S号点的费用是vi
2、如图所示,求n个矿井电力供应的最小花费,等价于求n + 1个点的最小生成树
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 310;
int n;
int w[N][N];
int dist[N];
bool st[N];
int prim()
{
memset(dist, 0x3f, sizeof dist);
dist[0] = 0;
int res = 0;
for (int i = 0; i < n + 1; i ++ )
{
int t = -1;
for (int j = 0; j <= n; j ++ )
if (!st[j] && (t == -1 || dist[t] > dist[j]))
t = j;
st[t] = true;
res += dist[t];
for (int j = 0; j <= n; j ++ ) dist[j] = min(dist[j], w[t][j]);
}
return res;
}
int main()
{
scanf("%d", &n);
for (int i = 1; i <= n; i ++ )
{
scanf("%d", &w[0][i]);
w[i][0] = w[0][i];
}
for (int i = 1; i <= n; i ++ )
for (int j = 1; j <= n; j ++ )
scanf("%d", &w[i][j]);
printf("%d\n", prim());
return 0;
}
acwing1145
有k个点可以通过卫星相连,就不用花费什么代价,那么可以考虑边最大的时候才使用卫星相连。
假设有给定一个d值,任意两个长度小于等于d的点,按照最小生成树的方式进行集合合并,形成m个连通块(m 棵最小生成树),则需要m个卫星设备
* 即找一个最小的d值,使得将所有权值大于d的边删去,之后,整个图形的连通块的个数等于k
#include <cstring>
#include <iostream>
#include <algorithm>
#include <cmath>
#define x first
#define y second
using namespace std;
typedef pair<int, int> PII;
const int N = 510, M = N * N / 2;
int n, k, m;
struct Edge
{
int a, b;
double w;
bool operator< (const Edge &t) const
{
return w < t.w;
}
}e[M];
PII q[M];
int p[N];
double get_dist(PII a, PII b)
{
int dx = a.x - b.x;
int dy = a.y - b.y;
return sqrt(dx * dx + dy * dy);
}
int find(int x)
{
if (p[x] != x) p[x] = find(p[x]);
return p[x];
}
int main()
{
cin >> n >> k;
for (int i = 0; i < n; i ++ ) cin >> q[i].x >> q[i].y;
for (int i = 0; i < n; i ++ )
for (int j = 0; j < i; j ++ )
e[m ++ ] = {i, j, get_dist(q[i], q[j])};
sort(e, e + m);
for (int i = 0; i < n; i ++ ) p[i] = i;
int cnt = n;
double res = 0;
for (int i = 0; i < m; i ++ )
{
if (cnt <= k) break;
int a = find(e[i].a), b = find(e[i].b);
double w = e[i].w;
if (a != b)
{
p[a] = b;
cnt -- ;
res = w;
}
}
printf("%.2f\n", res);
return 0;
}
这是一题求瓶颈生成树的题目。
瓶颈生成树 :无向图G的一颗瓶颈生成树是这样的一颗生成树,它最大的边权值在G的所有生成树中是最小的。
无向图的最小生成树一定是瓶颈生成树,但瓶颈生成树不一定是最小生成树。
命题:无向图的最小生成树一定是瓶颈生成树。
证明:可以采用反证法予以证明。
假设最小生成树不是瓶颈树,设最小生成树T的最大权边为e,则存在一棵瓶颈树Tb,其所有的边的权值小于w(e)。删除T中的e,形成两棵数T’, T’‘,用Tb中连接T’, T’‘的边连接这两棵树,得到新的生成树,其权值小于T,与T是最小生成树矛盾。
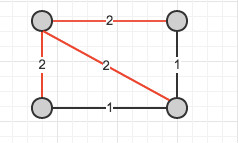
命题:瓶颈生成树不一定是最小生成树。
下面是一个反例:
POJ2395
给出n个农场和m条边,农场按1到n编号,现在有一人要从编号为1的农场出发到其他的农场去,求在这途中他最多需要携带的水的重量,注意他每到达一个农场,可以对水进行补给,且要使总共的路径长度最小。就是求最小生成树中的最长边。kruskal算法即可解决。
#include<iostream>
#include<cstdio>
#include<algorithm>
using namespace std;
#define N 2005
#define M 10005
struct Edge{
int u,v,w;
bool operator< (const Edge &W) const
{
return w<W.w;
}
}edge[M];
int mst=0,n,m,father[N],ans;
int find(int x)
{
return(father[x]==x?x:father[x]=find(father[x]));
}
void kruskal()
{
for(int i=1;i<=n;++i)
father[i]=i;
sort(edge+1,edge+m+1);
for(int i=1;i<=m;++i)
{
int f1=find(edge[i].u);
int f2=find(edge[i].v);
if(f1==f2) continue;
father[f1]=f2;
mst++;
if(mst==n-1)
{
ans=edge[i].w;
return;
}
}
}
int main()
{
scanf("%d%d",&n,&m);
for(int i=1;i<=m;++i)
scanf("%d%d%d",&edge[i].u,&edge[i].v,&edge[i].w);
kruskal();
printf("%d",ans);
return 0;
}
hdu4750
给无向边,q个查询。查询内容为: 给一个值 t ,询问符合要求的点对的总数。
对(u,v)的符合要求为:从u到v的每一种走法中,肯定有 一条或者多条 长度最长的边,每种走法的最长边必须大于等于 t。
而每种走法的最长边要大于等于t,那么就要找所有走法中最长的边中的最短>=t就可以了,此时要用到最小生成树!
首先(u,v)和(v,u)是不同的点对,所以最后答案一定是偶数。
那么对于图上任意点对,一定是在最小生成树(MST)上的,所以只要考虑(u,v)在MST上,(u,v)之间的最长一小段>=t就OK。
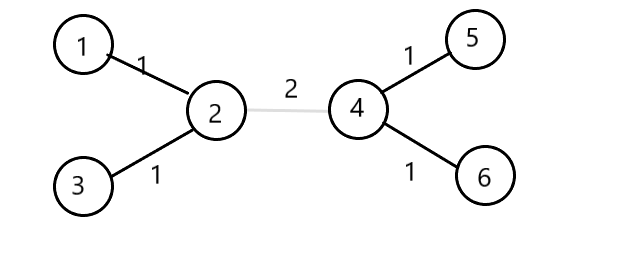
如图为这些点的最小生成树,虚线是kruskal连的最后一条边,那么如果有一个查询的t是 2 ,那么满足的点对一定是左边三个×右边三个 (1,2,3) × (4,5,6)一共有9对,由于(u,v)可以再对称一对(v,u),所以对于查询 t=2 ,答案是18;
而对于查询 t=1来说,查询t=2的答案一定也是查询t=1的一部分,也就是说,查询t=2的答案可以再加到查询t=1上;
这里我们就发现,可以对查询进行离线操作,将其排好序;
假设查询数目为6,分别为(2,3,6,7,7,10),
kruskal的加入的边为(1,2,4,5,6,8,10,11),
一共有八条边,我们一条一条来考虑:
第一条:1 它连上面的查询中最小的都不能满足,ans[第一个查询]=0;
第二条:2 它满足 2 的查询,于是这条边两边连的连通块的点对加到ans[第二个查询];
第三条:4 它满足查询2和3,但是我们此时只把答案给3,因为可以把3的答案加到2上;
第四条:5 它满足查询2和3,和上一条边一样,此时要把这条边的答案加到3上,最后答案都会给前面的2上的。
第五条:6 它满足查询2,3,6,同上,答案只给6;
第六条:8 同上,满足的有5条,但只把答案给7,发现有两个7,也没关系,把答案给后面那个7,那么前面的7的答案就是0。之后可以把后面的7的答案加到前面的7上,两个7的答案最后是一样的。
第七条:10 满足查询10;
第八条:11 满足所有查询,和第四条边一样,加到查询10;
由此发现,每条边的答案都是加给最后那个小于等于该条边长度的查询;
最后!后面的查询的答案是可以加到前面的查询上的!
#include <bits/stdc++.h>
using namespace std;
const int N=100010,M=500010;
struct Edge
{
int u,v,w;
bool operator< (const Edge &W) const
{
return w<W.w;
}
}e[M];
int p[N],num[N],len[N],pre[N],presum[N];
int n,m,q;
int cnt;
int find(int x)
{
if(x != p[x])
p[x]=find(p[x]);
return p[x];
}
int main()
{
while(~scanf("%d%d",&n,&m))
{
memset(pre,0,sizeof pre);
for(int i=1;i<=m;i++)
{
scanf("%d%d%d",&e[i].u,&e[i].v,&e[i].w);
}
sort(e+1,e+m+1);
for(int i=0;i<n;i++)
{
p[i]=i;
num[i]=1;
}
cnt=0;
for(int i=1;i<=m;i++)
{
int fu,fv,sum;
fu=find(e[i].u);
fv=find(e[i].v);
if(fu!=fv)
{
p[fv]=fu;
sum=num[fu]*num[fv];
num[fu]+=num[fv];
cnt++;
len[cnt]=e[i].w;
pre[cnt]=sum;
}
if(cnt==n-1) break;
}
for(int i=cnt-1;i>=1;i--)
{
pre[i]+=pre[i+1];
}
scanf("%d",&q);
while(q--)
{
int x;
scanf("%d",&x);
int t=lower_bound(len+1,len+cnt+1,x)-len;
printf("%d\n",pre[t]*2);
}
}
return 0;
}
hdu3938
所谓“离线”,就是把所有的数据都输入之后再计算,“在线”就是边输入边计算。
用在这题中,是因为输入中的“询问部分”,有Q 个问,每个L可以有多少种不同路径。由于大的L必定会包含到小的L, 所以把所有问题都输入,再从大到小排序,再计算,可以减少很多计算量。
这题还需要用到的是并查集中的“权值”, 用size数组表示,也就是某个棵树k有size[k]个结点。同一个树之间的点都是连通的,任何点都可以通往其它的任意点, 那么当两颗树合并成一棵树时, 将会增加size[a]*size[b]条路径。
#include<iostream>
#include<cstdio>
#include<algorithm>
using namespace std;
#define N 10005
int f[N], size[N], ans[N], n, m, Q;
struct Edge{
int u, v, val;
bool operator< (const Edge &W) const
{
return val<W.val;
}
}arr[N*5];
struct Query
{
int id, L;
bool operator< (const Query &W) const
{
return L<W.L;
}
}q[N];
int find(int x)
{
if(x != f[x])
f[x]=find(f[x]);
return f[x];
}
int main(){
while(~scanf("%d%d%d",&n,&m,&Q))
{
for(int i=0; i<m; ++i)
scanf("%d%d%d",&arr[i].u,&arr[i].v,&arr[i].val);
for(int i=0; i<Q; ++i)
{
scanf("%d",&q[i].L);
q[i].id=i;
}
sort(arr,arr+m);
sort(q,q+Q);
int cnt=0, j=0;
for(int i=1; i<=n; ++i)
f[i]=i, size[i]=1;
for(int i=0; i<Q; ++i)
{
while(j<m && arr[j].val<=q[i].L)
{
int a=find(arr[j].u), b=find(arr[j].v);
//cout<<"------"<<a<<' '<<b<<endl;
if(a != b)
{
cnt += size[a]*size[b];
size[b] += size[a];
f[a] = b;
}
j++;
}
ans[q[i].id] = cnt;
}
for(int i=0; i<Q; ++i)
printf("%d\n", ans[i]);
}
return 0;
}
krusral重构树求最小瓶颈路
最小瓶颈路:给定加权无向图的两个节点u和v,求出从u到v的一条路径,使得路劲上的最长边尽量短(最小生成树的最长边)或最小边尽量长(最大生成树的最小边)。
最大生成树最小边权
思路
1.kruskal建最大生成树
2.bfs维护两个数组,一个fa[i][k]存最近公共祖先,一个dist[i][k]存路径最小值
3.lca
第一步
首先,为什么要用kruskal建最大生成树呢? 因为题目让我们求
每辆车在不超过车辆限重的情况下,最多能运多重的货物
简化题意就是:让路径上最小值最大。
且因为题目输入给出的可能是图,所以我们可以存图并用kruskal构造最大生成树
第二步
因为我们已经用kruskal得到了最大生成树,这时点到点的距离是唯一的,所以我们可以跑dfs维护所需信息,为之后的lca做准备
平时我们做lca之需要维护fa数组,fa[i][j]存放 i位置的2^j祖先。现在因为我们要保存路径上的最小值,所以还需要维护dist数组,dist[i][j]存放 i到i的2^j祖先间的路径权值最小值。
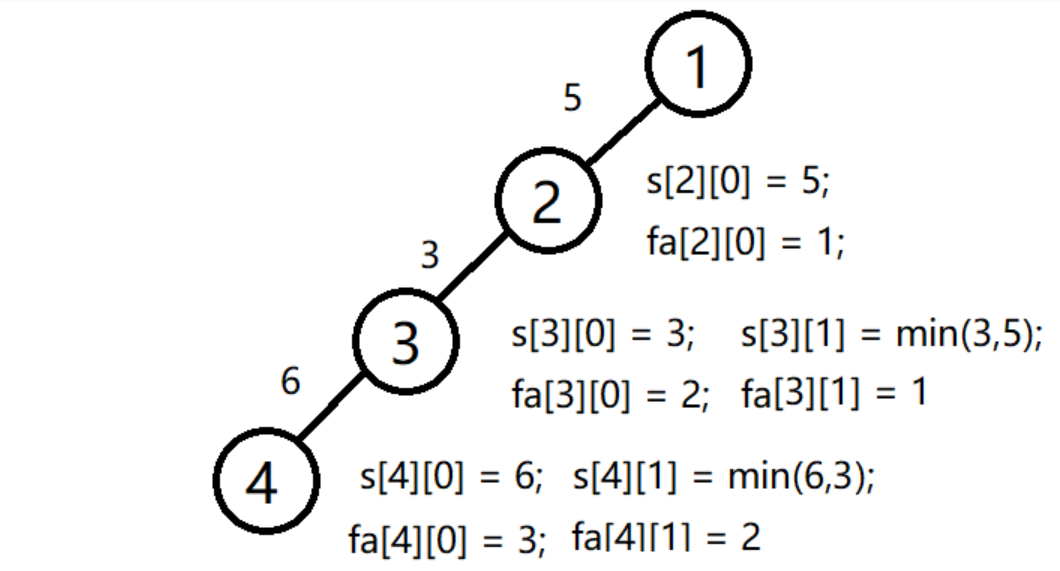
第三步
咱们已经通过bfs存储了fa数组和dist数组,先一步就是我们的lca了,我们可以通过求两点间的最近公共祖先来求 路径上的最小值
这里要注意,不管在什么时候移动,都要修改最小值。
我们发现x和y不在同一层上,所以我们要将x想上移动,同时更新最小值
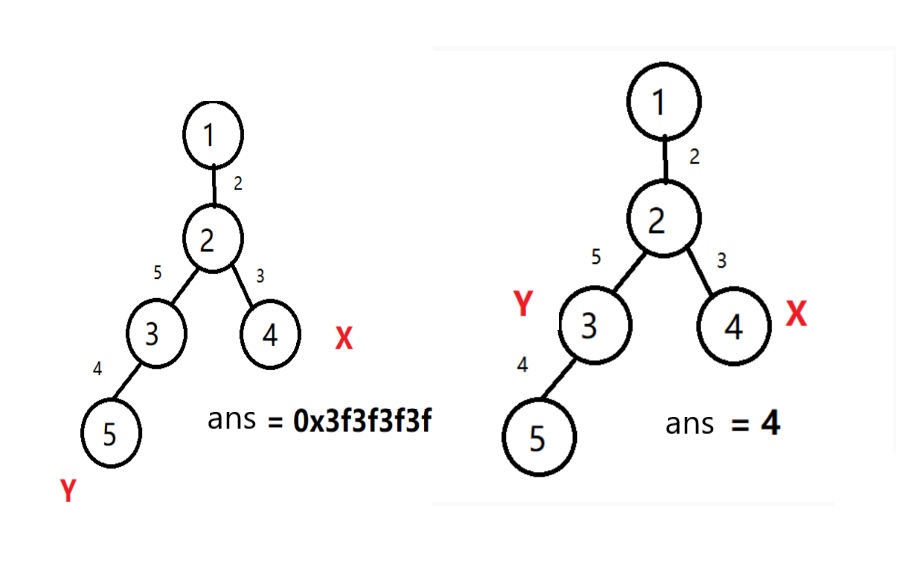
x和y在同一层上之后,我们将x和y同时向上移动,更新最小值
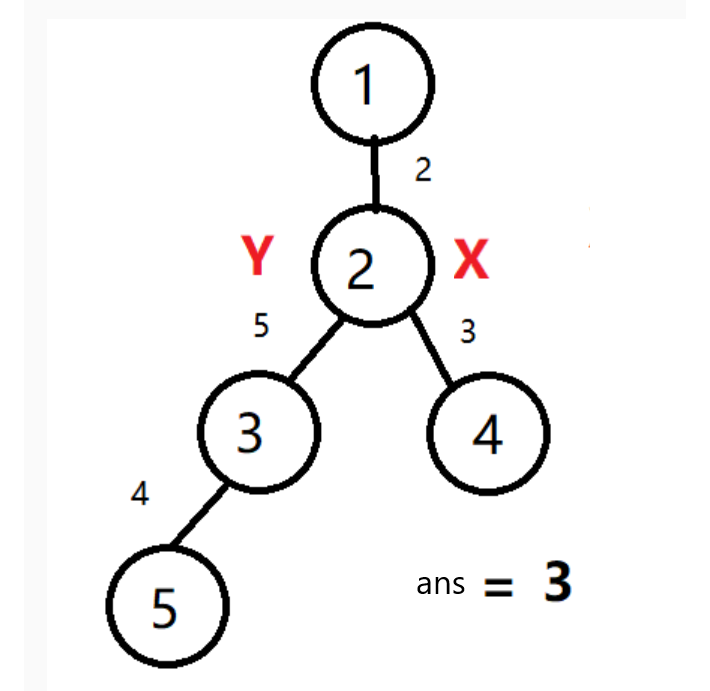
#include<iostream>
#include<algorithm>
#include<cstring>
#include<cmath>
#include<cstdio>
using namespace std;
const int N=10010,M=50010,INF=0x3f3f3f3f;
int h[N],e[N<<1],ne[N<<1],w[N<<1],idx;
struct Edge
{
int a,b,w;
bool operator< (const Edge &W) const
{
return w>W.w;
}
}edge[M];
int n,m,Q,d;
int p[N];
bool st[N];
int depth[N];
int fa[N][15];
int dist[N][15];
int q[N];
int find(int x)
{
if(x != p[x])
p[x]=find(p[x]);
return p[x];
}
void add(int a,int b,int c)
{
e[idx]=b,w[idx]=c,ne[idx]=h[a],h[a]=idx++;
}
void krustral()
{
sort(edge+1,edge+m+1);
for(int i=1;i<=n;i++)
p[i]=i;
for(int i=1;i<=m;i++)
{
int a=find(edge[i].a),b=find(edge[i].b);
if(a != b)
{
p[a]=b;
add(edge[i].a,edge[i].b,edge[i].w);
add(edge[i].b,edge[i].a,edge[i].w);
}
}
}
void bfs(int root)//初始化
{
depth[0]=0;
depth[root]=1;
st[root]=true;
int hh=0,tt=0;
q[0]=root;
while(hh <= tt)
{
int t=q[hh++];
for(int i=h[t];~i;i=ne[i])
{
int j=e[i];
if(depth[j] > depth[t] + 1)
{
depth[j]=depth[t] + 1;
st[j]=true;
q[++tt]=j;
fa[j][0]=t;
dist[j][0]=w[i];
for(int k=1;k<=d;k++)
{
fa[j][k]=fa[fa[j][k-1]][k-1];
dist[j][k]=min(dist[j][k-1],dist[fa[j][k-1]][k-1]);
//cout<<"---"<<j<<' '<<k<<' '<<dist[j][k]<<endl;
}
}
}
}
}
int lca(int x,int y)
{
if(find(x) != find(y))
return -1;
int ans=INF;
if(depth[x] > depth[y])
swap(x,y);
for(int i=d;i>=0;i--)
if(depth[fa[y][i]] >= depth[x])
{
ans=min(ans,dist[y][i]);
// cout<<"---"<<y<<' '<<i<<' '<<ans<<endl;
y=fa[y][i];
}
if(x == y)
return ans;
for(int i=d;i>=0;i--)
if(fa[x][i] != fa[y][i])
{
ans=min(ans,min(dist[x][i],dist[y][i]));
x=fa[x][i];
y=fa[y][i];
}
ans=min(ans,min(dist[x][0],dist[y][0]));
return ans;
}
int main()
{
// freopen("test.in.txt","r",stdin);
// freopen("test.out","w",stdout);
cin>>n>>m;
d=log2(n)+1;
memset(h,-1,sizeof h);
memset(depth,0x3f,sizeof depth);
memset(dist,0x3f,sizeof dist);
for(int i=1;i<=m;i++)
{
int a,b,c;
scanf("%d%d%d",&a,&b,&c);
edge[i]={a,b,c};
}
krustral();
for(int i=1;i<=n;i++)
if(!st[i])
bfs(i);
cin>>Q;
while(Q--)
{
int a,b;
scanf("%d%d",&a,&b);
printf("%d\n",lca(a,b));
}
return 0;
}
最小生成树的最大边权
最小瓶颈路+最短路
UVA10186
我们发现这道题有两个限制温度和长度,不好处理,所以我们要去消除一层限制。
因为要首先保证最高温度尽量小,所以先考虑温度,求最小瓶颈路,跑出s到t的最高温度的最小值ans。
然后把温度不大于ans的边加入图中,跑最短路记录路径即可。
#include<iostream>
#include<algorithm>
#include<cstring>
#include<cmath>
#include<cstdio>
#include<queue>
using namespace std;
typedef pair<double,int> PII;
const int N=110,M=10010,INF=0x3f3f3f3f;
int h[N],e[M<<1],ne[M<<1],idx;
double w[M<<1];
struct Edge
{
int a,b;
double tem,w;
bool operator< (const Edge &W) const
{
return tem<W.tem;
}
}edge[M];
int n,m,s,t;
int p[N];
bool st[N];
double ans;
double dist[N];
int pre[N];
int find(int x)
{
if(x != p[x])
p[x]=find(p[x]);
return p[x];
}
void add(int a,int b,double c)
{
e[idx]=b,w[idx]=c,ne[idx]=h[a],h[a]=idx++;
}
void krustral()
{
sort(edge+1,edge+m+1);
for(int i=1;i<=n;i++)
p[i]=i;
for(int i=1;i<=m;i++)
{
int a=find(edge[i].a),b=find(edge[i].b);
if(a != b)
{
p[a]=b;
if(find(s) == find(t))
{
ans=edge[i].tem;
return;
}
}
}
}
void dijkstra()
{
for(int i=1;i<=n;i++)
dist[i]=INF;
memset(st,0,sizeof st);
dist[s]=0;
priority_queue<PII,vector<PII>,greater<PII> > heap;
heap.push({0,s});
while(heap.size())
{
PII t=heap.top();
heap.pop();
int ver=t.second;
if(st[ver])
continue;
st[ver]=true;
for(int i=h[ver];i!=-1;i=ne[i])
{
int j=e[i];
if(st[j])
continue;
if(dist[j]>dist[ver]+w[i])
{
dist[j]=dist[ver]+w[i];
heap.push({dist[j],j});
pre[j]=ver;
}
}
}
}
void print_path(int s,int t)
{
if(s == t)
{
printf("%d",s);
return;
}
print_path(s,pre[t]);
printf(" %d",t);
}
int main()
{
while(~scanf("%d%d",&n,&m))
{
memset(h,-1,sizeof h);
idx=0;
cin>>s>>t;
for(int i=1;i<=m;i++)
{
int a,b;
double c,tem;
scanf("%d%d%lf%lf",&a,&b,&tem,&c);
edge[i]={a,b,tem,c};
}
krustral();
for(int i=1;i<=m;i++)
if(edge[i].tem <= ans)
{
add(edge[i].a,edge[i].b,edge[i].w);
add(edge[i].b,edge[i].a,edge[i].w);
}
dijkstra();
print_path(s,t);
cout<<endl;
//printf("%.1f\n",dist[t]);
printf("%.1f %.1f\n",dist[t],ans);
}
return 0;
}
acwing346
将一个最小生成树的图,添加一些边,使得这张图成为一个完全图.
但是我们这张图的最小生成树,必须还是原来那张图的最小生成树.
也就是说两张图的最小生成树表示是一模一样的.



#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 6010;
int n;
struct Edge
{
int a, b, w;
bool operator< (const Edge &t) const
{
return w < t.w;
}
}e[N];
int p[N], Size[N];
int find(int x)
{
if (p[x] != x) p[x] = find(p[x]);
return p[x];
}
int main()
{
int T;
cin >> T;
while (T -- )
{
cin >> n;
for (int i = 0; i < n - 1; i ++ )
{
int a, b, w;
cin >> a >> b >> w;
e[i] = {a, b, w};
}
sort(e, e + n - 1);
for (int i = 1; i <= n; i ++ ) p[i] = i, Size[i] = 1;
int res = 0;
for (int i = 0; i < n - 1; i ++ )
{
int a = find(e[i].a), b = find(e[i].b), w = e[i].w;
if (a != b)
{
res += (Size[a] * Size[b] - 1) * (w + 1);
Size[b] += Size[a];
p[a] = b;
}
}
cout << res << endl;
}
return 0;
}
次小生成树

如果要求的是非严格次小生成树,只需枚举每条非树边,替换该非树边所形成的环上的最大边权。
如果要求的是严格次小生成树,不仅要求最大边权,还要处理次大边权(因为当最大树边和当前枚举的非树边长度相同时,就不能替换了,但此时却可以替换长度次大的树边。因此还需同时预处理出长度次大的树边。)。
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
typedef long long LL;
const int N = 510, M = 10010;
int n, m;
struct Edge
{
int a, b, w;
bool f;
bool operator< (const Edge &t) const
{
return w < t.w;
}
}edge[M];
int p[N];
int dist1[N][N], dist2[N][N];
int h[N], e[N * 2], w[N * 2], ne[N * 2], idx;
void add(int a, int b, int c)
{
e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++ ;
}
int find(int x)
{
if (p[x] != x) p[x] = find(p[x]);
return p[x];
}
void dfs(int u, int fa, int maxd1, int maxd2, int d1[], int d2[])
{//maxd1为从根节点出发向下遍历的边权最大值,maxd2为次大值
d1[u] = maxd1, d2[u] = maxd2;
for (int i = h[u]; ~i; i = ne[i])
{
int j = e[i];
if (j != fa)
{
int td1 = maxd1, td2 = maxd2;
if (w[i] > td1) td2 = td1, td1 = w[i];
else if (w[i] < td1 && w[i] > td2) td2 = w[i];
dfs(j, u, td1, td2, d1, d2);
}
}
}
int main()
{
scanf("%d%d", &n, &m);
memset(h, -1, sizeof h);
for (int i = 0; i < m; i ++ )
{
int a, b, w;
scanf("%d%d%d", &a, &b, &w);
edge[i] = {a, b, w};
}
sort(edge, edge + m);
for (int i = 1; i <= n; i ++ ) p[i] = i;
LL sum = 0;
for (int i = 0; i < m; i ++ )
{
int a = edge[i].a, b = edge[i].b, w = edge[i].w;
int pa = find(a), pb = find(b);
if (pa != pb)
{
p[pa] = pb;
sum += w;
add(a, b, w), add(b, a, w);
edge[i].f = true;
}
}
for (int i = 1; i <= n; i ++ ) dfs(i, -1, 0, 0, dist1[i], dist2[i]);
LL res = 1e18;
for (int i = 0; i < m; i ++ )
if (!edge[i].f)
{
int a = edge[i].a, b = edge[i].b, w = edge[i].w;
LL t;
if (w > dist1[a][b])
t = sum + w - dist1[a][b];
else if (w > dist2[a][b])
t = sum + w - dist2[a][b];
res = min(res, t);
}
printf("%lld\n", res);
return 0;
}
增量最小生成树
所谓最小增量生成树问题,即:给定包含 n 个点的空图,依次加入 m 条带权边,每次加入一条边,就输出当前图中最小生成树的权值,如果没有生成树,则输出无解
求解最小增量生成树的方法是:根据最小生成树的回路性质,在原有最小生成树的基础上,每次增加一条边就会构成一个回路,那么去掉这个回路上权值最大的边,得到的就是新的最小生成树。
简单来说,每一次加边之前先跑一遍 Kruskal 找最小生成树,若已经有最小生成树,则新加入的边肯定会让其形成环,这时候开始进行删边操作,删去那个多余的边即可。


这篇使我目前见过最长的orz