原文有发在洛谷上,如果图片咕掉了可以去翻一翻那篇博文
前言:
$ $
$\quad\quad$ 不得不说,树真是一种神奇的数据结构呢。
$\quad\quad$ 即使是在图论的某些经典问题中,也可以看到它的身影。
$\quad\quad$ 比如说:解决最短路问题的最短路树。
$\quad\quad$ 比如说:解决瓶颈路问题的克鲁斯卡尔重构树。
$\quad\quad$ 以及下面要介绍的:解决最小割问题的最小割树。
$\quad\quad$ 什么?你说你完全没听说过上面那三个玩意?
$ $
$\quad$ 前置芝士:
-
$\quad\quad$ 最大流算法(至少要会Dinic)
-
$\quad\quad$ 最小割的概念与最小割最大流定理(最小割等于最大流)
-
$\quad\quad$ 树上倍增基础(这个应该都会吧)
-
$\quad\quad$ 简单的分治思想(提高组水平的样子)
$ $
$\quad$ 注:本文为了便于理解,并没有使用标准的数学语言进行表达和证明。
$ $
目录:
$\quad\quad$ $1-1:$ 问题引入
$\quad\quad$ $1-2:$ 问题探究
$\quad\quad$ $2-2:$ 定理证明
$\quad\quad$ $2-1:$ 引理证明
$\quad\quad$ $3-1:$ 最小割树定义
$\quad\quad$ $3-2:$ 最小割树构建
$\quad\quad$ $3-3:$ 最小割树性质
$\quad\quad$ $4:$ 代码与练习
$ $
正文:
$ $
$\quad$ $1-1:$问题引入:给定一张$n$个点,$m$条边的无向图,求 任意两点间 的最小割。
$\quad\quad$ 题意很显然,以下图为例,就是求(1,2)之间,(1,3)之间,(1,4)之间,(2,3)之间,(2,4)之间,(3,4)之间的最小割。
$\quad\quad$ 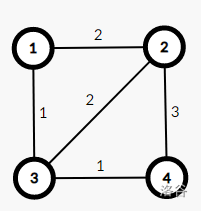
$\quad\quad$ 也就是说,我们要求 $\frac{n*(n-1)}{2}$ 组最小割。
$ $
$\quad$ $1-2:$问题探究:
$\quad\quad$ 本题朴素做法是跑 $\frac{n*(n-1)}{2}$ 遍 Dinic,复杂度是 $O(n^2m*n^2)=O(n^4m)$。
$\quad\quad$ 即使最大流算法的复杂度很难达到上界,这个复杂度也显然不可接受。
$\quad\quad$ 能否获得更优的复杂度?(当然可以,不然我写这个干嘛)
$\quad\quad$ 对我们的复杂度进行分析:前面的 $O(n^2m)$ 是Dinic的复杂度,存在优化空间,但不大(ISAP/HLPP 并不比 Dinic 快特别多)。
$\quad\quad$ 后面的 $O(n^2)$ 是枚举点对的复杂度,我们考虑对这一部分进行优化。
$\quad\quad$ 如果我们打表观察上图各个点之间的最小割的数值(如下图)。
| $P_1$ | $P_2$ | $P_3$ | $P_4$ | |
|---|---|---|---|---|
| $P_1$ | 0 | 3 | 3 | 3 |
| $P_2$ | 3 | 0 | 4 | 4 |
| $P_3$ | 3 | 4 | 0 | 4 |
| $P_4$ | 3 | 4 | 4 | 0 |
$\quad\quad$ 我们会发现,表中仅有 $3,4$ 两个数。
$\quad\quad$ 是否能够猜想:对于一张 $n$ 个点的图来说,点对间最小割的数值其实远小于 $n^2$ 种?
$\quad\quad$ 这就涉及到了一个定理:给定一张 $n$ 个点的无向图,最多只有 $n-1$ 种本质不同(也可理解成值不同)的最小割。
$\quad\quad$ 如何证明这个定理?(当然是归纳法呐)
$\quad\quad$ 又如何利用该定理优化算法复杂度?
$ $
$ $
$\quad$ $2-1:$定理证明(建议跳过):
$\quad\quad$ 定理表述:给定一张 $n$ 个点的无向图,最多只有 $n-1$ 种本质不同的最小割。
$\quad\quad$ 以下图为例加以证明:
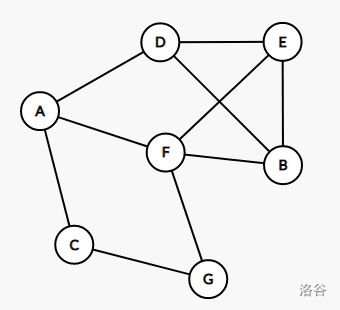
$\quad\quad$ 我们令 $\operatorname{Cut}(A,B)$ 表示在原图内 $A,B$ 之间最小割所包含边的集合(在公式中出现时表示这些边的权值和)。
$\quad\quad$ 注意:$\operatorname{Cut}(A,B)$ 在本文的任何地方,
都代表 原图 中 $A,B$ 之间的最小割所包含的边集。
$\quad\quad$ 显然, 割去 $\operatorname{Cut}(A,B)$ 后,整张图分成两个联通部分,就像下面这样:
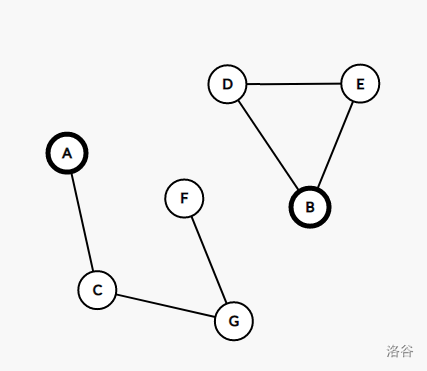
$\quad\quad$ 根据引理三(引理表述及证明在定理的后面),对于 $A$ 所在连通块中的任一点 $X$,都有 $\operatorname{Cut}(B,X) = \min(\operatorname{Cut}(A,B),\operatorname{Cut}(A,X))$。
$\quad\quad$ 我们不妨再尝试在原图中割掉 $\operatorname{Cut}(A,C)$。
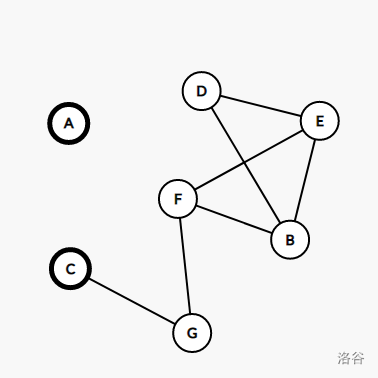
$\quad\quad$ 同样根据引理三,对于 $C$ 所在连通块中的任一点 $Y$,都有 $\operatorname{Cut}(A,Y) = \min(\operatorname{Cut}(A,C),\operatorname{Cut}(C,Y))$。
$\quad\quad$ 看出什么了吗?如果把这里的 $Y$ 和之前的 $X$ 取为同一个点(当然,要求这个点同时满足上面两式中 $X$ 与 $Y$ 所满足的的条件),就可以把这两个式子整合成一个式子。
$\quad\quad$ 比如说,取 $X=Y=G$,有$\operatorname{Cut}(B,G) = \min(\operatorname{Cut}(A,B),\operatorname{Cut}(A,G))$,$\operatorname{Cut}(A,G) = \min(\operatorname{Cut}(A,C),\operatorname{Cut}(C,G))$。
$\quad\quad$ 带入得$\operatorname{Cut}(B,G) = \min(\operatorname{Cut}(A,B),\operatorname{Cut}(A,C),\operatorname{Cut}(C,G))$。
$\quad\quad$ 我们不妨再尝试分别割掉 $\operatorname{Cut}(C,G)$ 和 $\operatorname{Cut}(F,G)$,看看还会得到哪些式子。
$\quad\quad$ 这里列举割去上述几组 $cut$ 并进行转化后,只关于 $A,C,G,F$ 四点的式子:
$\quad\quad$ $\operatorname{Cut}(A,C),\operatorname{Cut}(C,G),\operatorname{Cut}(F,G)$
$\quad\quad$ $\operatorname{Cut}(A,G) = \min(\operatorname{Cut}(A,C),\operatorname{Cut}(C,G))$
$\quad\quad$ $\operatorname{Cut}(A,F) = \min(\operatorname{Cut}(A,C),\operatorname{Cut}(C,G),\operatorname{Cut}(G,F))$
$\quad\quad$ $\operatorname{Cut}(C,F) = \min(\operatorname{Cut}(C,G),\operatorname{Cut}(G,F))$
$\quad\quad$ 至此,我们可以看出,给出一些诸如 $\operatorname{Cut}(A,C),\operatorname{Cut}(C,G),\operatorname{Cut}(G,F)$之类的“单位元”,我们就可以表示出 $A,C,G,F$ 中任意两点间的最小割。
$\quad\quad$ 这些“单位元”到底是什么?很容易看出来,这些“单位元”就是我们所割去的边集。
$\quad\quad$ 当然,我们不是任意割边的,这里割边要求其实与最小割树构造时的割边要求是相同的。
$\quad\quad$ 也就是说,我们所选择割掉的 $Cut(X,Y)$ 中的 $X$ 与 $Y$ 必须在之前所选择的边被割掉之后任然连通。
$\quad\quad$ (如果想知道割边的具体选择过程,可以参考下文中的 最小割树的构建 内容,此处不详解)
$\quad\quad$ 考虑连通性:我们每次割的过程会把某两个连通的点变得不连通。
$\quad\quad$ 因此,我们每一次“割”的过程,都会把一个原有的连通块分成两个新的连通块,即连通块个数 $+1$,又因为我们最多有 $n$ 个连通块(每个点各算一个),所以我们最多割 $n-1$ 次,故最多有 $n-1$ 个单位元。
$\quad\quad$ 因为某两个点之间的最小割的值本质上就是对某一些“单位元”进行 $\min$ 操作,所以给定一张 $n$ 个点的无向图,最多只有 $n-1$ 种本质不同的最小割。
$\quad\quad$ (总感觉这里没讲清楚,如果没有看懂证明可以先通读全文,尤其是下文关于 最小割树 的干货,然后再回来看定理证明 [虽然我个人觉得不会有人在意这个的证明])
$ $
$\quad$ $2-2:$引理证明(建议跳过):
$\quad\quad$ 注:以下大小写字母等价,小写字母表示原图操作后的情况。
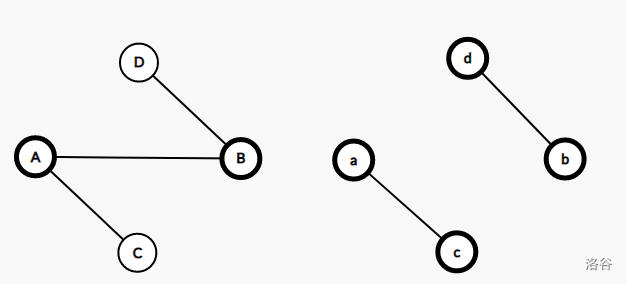
- $\quad\quad$ 引理一:任取连通两点 $A,B$,割去 $\operatorname{Cut}(A,B)$ 之后,图分为两个连通块,取 $C$ 为 $A$ 所在连通块中的任一点, $D$ 为 $B$ 所在连通块中的任一点,有 $\operatorname{Cut}(A,B) \ge \operatorname{Cut}(C,D)$
。
$\quad\quad$ 证明一:假设 $\operatorname{Cut}(A,B) < \operatorname{Cut}(C,D)$,那么,割断 $\operatorname{Cut}(A,B)$ 后,$\operatorname{Cut}(C,D)$ 并没有被割断,$C$ 与 $D$ 连通,而 $A$ 与 $C$ 在同一连通块内,故 $A$ 与 $C$ 连通,同理,$B$ 与 $D$ 连通,所以 $A,B$ 任然连通,与 $A,B$ 被割断这一事实矛盾,引理得证(这个引理很好感性理解来着)。
$ $
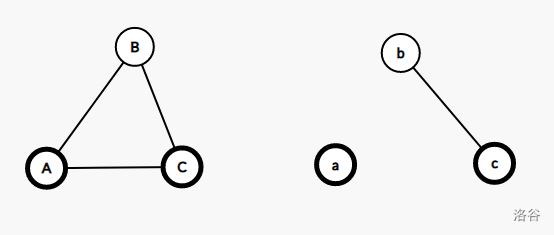
- $\quad\quad$ 引理二:任取不同的三点 $A,B,C$,有 $\operatorname{Cut}(A,C) \ge \min(\operatorname{Cut}(A,B),\operatorname{Cut}(B,C))$。
$\quad\quad$ 证明二:割去 $\operatorname{Cut}(A,C) $,不妨假设割断后$B , C$ 两点任然连通(若 $B,C$ 不连通,那么 $A,B$ 一定连通,故同理即可)。由引理一得:$\operatorname{Cut}(A,C) \ge \operatorname{Cut}(A,B)$,故$\operatorname{Cut}(A,C) \ge \min(\operatorname{Cut}(A,B),\operatorname{Cut}(B,C))$(大于 $\min$ 中的任意一个值,就必定恒大于 $\min$),引理得证(这玩意可以类比三角形两边之和大于第三边,不过这里不是和,而是最小值)。
$ $
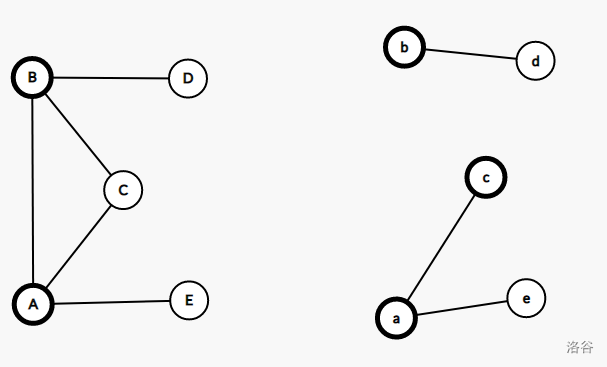
- $\quad\quad$ 引理三:任取连通两点 $A,B$,割去 $\operatorname{Cut}(A,B)$ 之后,图分为两个连通块,若 $C$ 与 $A$ 连通,则有 $\operatorname{Cut}(B,C) = \min(\operatorname{Cut}(A,B),\operatorname{Cut}(A,C))$。
$\quad\quad$ 证明三:根据引理一,有: $\operatorname{Cut}(A,B) \ge \operatorname{Cut}(B,C)$,根据引理二,又有 $\operatorname{Cut}(B,C) \ge \min(\operatorname{Cut}(A,B),\operatorname{Cut}(A,C))$。
$\quad\quad$ 下面分情况讨论:
$\quad\quad$ 假如 $\operatorname{Cut}(A,B)\le\operatorname{Cut}(A,C)$,那么$\operatorname{Cut}(B,C) \ge \min(\operatorname{Cut}(A,B),\operatorname{Cut}(A,C))=\operatorname{Cut}(A,B)$,又$\operatorname{Cut}(A,B) \ge \operatorname{Cut}(B,C)$,故$ \operatorname{Cut}(B,C)=\operatorname{Cut}(A,B)=\min(\operatorname{Cut}(A,B),\operatorname{Cut}(A,C))$,所证等式成立。
$\quad\quad$ 假如 $\operatorname{Cut}(A,B)>\operatorname{Cut}(A,C)$,那么考虑在原图中割断 $\operatorname{Cut}(A,C)$。
$\quad\quad$ $\quad\quad$ 假若割断后 $A,B$ 不连通,那么 $\operatorname{Cut}(A,B)$ 显然不是割断 $A,B$ 的最优解,与条件矛盾。
$\quad\quad$ $\quad\quad$ 假若割断后 $A,B$ 连通,那么根据引理一,有 $\operatorname{Cut}(A,C)\ge\operatorname{Cut}(B,C)$,又因为$\operatorname{Cut}(B,C) \ge \min(\operatorname{Cut}(A,B),\operatorname{Cut}(A,C)) = \operatorname{Cut}(A,C)$,故假设与条件矛盾。
$\quad\quad$ 因此,当 $\operatorname{Cut}(A,B)\le\operatorname{Cut}(A,C)$ 时,等式成立,而 $\operatorname{Cut}(A,B)>\operatorname{Cut}(A,C)$ 的情况不可能出现。引理得证(这个引理其实可以看做引理二在割边后的特殊形式,在式子上不过是把引理二的大于等于换成了等于)。
$ $
$ $
$\quad$ $3-1:$最小割树定义:
$\quad\quad$ 最小割树(Gomory-Hu Tree)主要用来解决点对之间最小割问题。
$\quad\quad$ 它利用 给定一张 $n$ 个点的无向图,任意两点间的最小割数值最多只有 $n-1$ 种 这一定理,把图上跑的最小割问题,转化为了树上某一路径上边权的最小值的问题,以降低多次询问某两点间最小割的复杂度。
$\quad\quad$ 其定义是:定义一棵树 $T$ 为最小割树,当且仅当对于树上的所有边$(s,t)$,树上去掉$(s,t)$后产生的两个连通块中的点的集合,恰好是原图上$(s,t)$的最小割把原图分成的两个连通块中的点的集合,且边$(u,v)$的权值等于原图上$(u,v)$的最小割。
$ $
$\quad$ $3-2:$最小割树构建:
$\quad\quad$ 1.于当前连通块中任取两个点 $x,y$ ,求出两点在原图中的最小割 $cut$(注意是原图)。
$\quad\quad$ 2.于最小割树中建立连接 $x,y$ 的边,边权为 $cut$。
$\quad\quad$ 3.在当前连通块内也割去 $cut$,于割去 $cut$ 后分裂成的两个新连通块内分别重复 1,2 ,3 过程,直到当前连通块仅剩一个点。
$\quad\quad$ 示例(大写字母组成的是图,小写字母组成的是最小割树,加粗的大写字母是接下来要割的节点,每个块内接下来要割的节点可任意选定):
$\quad\quad$ 选中点 $A,B$。
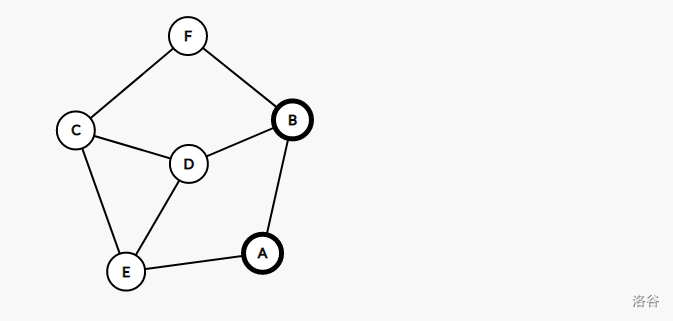
$\quad\quad$ 割开 $A,B$。于最小割树中建边,在两个新的连通块内分别选中 $B,C$ 节点和 $A,E$ 节点。
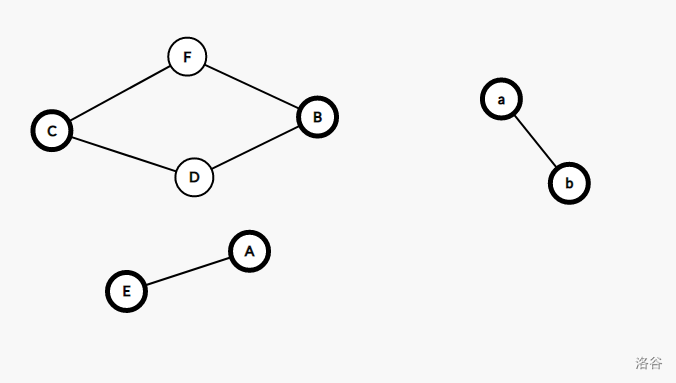
$\quad\quad$ 割开,建边,再选中。
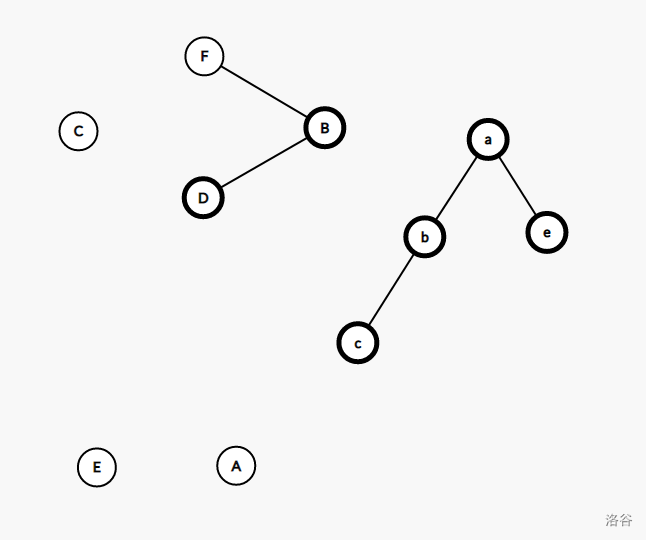
$\quad\quad$ 重复过程,直到最后(这里直接跳到最后),得到最小割树。
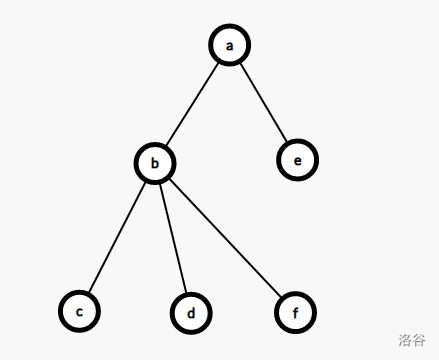
$\quad\quad$ 看上去,最小割树的构造过程很麻烦,其实在代码层面上并非如此。
$\quad\quad$ 我们可以利用分治思想,简单地构造最小割树,代码放于算法讲解之后,如有兴趣可以提前查看。
$ $
$\quad$ $3-3:$最小割树性质:
$\quad\quad$ 最小割树有一个神奇的性质:原图中任意两点间的最小割等价于最小割树上这两点路径上的边权的最小值。
$\quad\quad$ 构造演示的图中并未标出边权权值,这里给出一张样例图和其最小割树,建议读者自己也动手试一试。
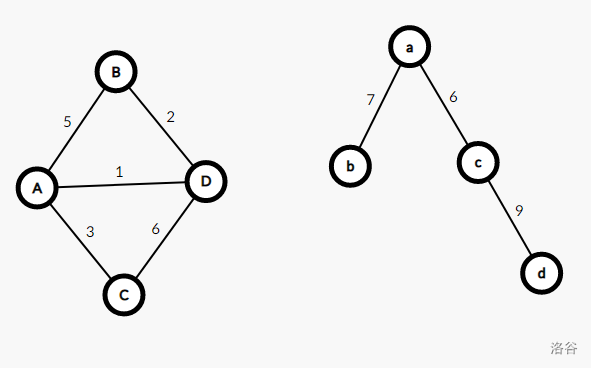
$\quad\quad$ 利用这一性质,所有对原图中两点间最小割的询问都可以被转化为树上最小值的问题,倍增算法即可解决。
$\quad\quad$ 假设原图有 $n$ 个点,$m$ 条边,询问 $Q$ 次最小割,那么朴素做法复杂度是 $O(n^2m*Q)$,储存已经计算过的值可以使复杂度降至 $O(n^2m*\min(Q,n^2))$,可看做 $O(n^4m)$。
$\quad\quad$ 而最小割树复杂度是 $O(n^2m*n+Q*logn)$,可以看做 $O(n^3m)$。
$\quad\quad$ 关于最小割树性质的证明,其实已经在之前的证明(尤其是引理三)中出现了大半了,这里就不赘述了。
$ $
$ $
$\quad$ $4:$代码与练习(代码以洛谷P4897 【模板】最小割树为例):
$\quad\quad$ 最小割树最麻烦的地方在于构建,这里分析构建的实现:
$\quad\quad$ 我们知道,最小割树构建的时候是要处理连通块的分裂(割去某些边,变成两个连通块,然后分别递归处理)的,难道我们真的作一个图然后一次次的分裂吗?
$\quad\quad$ 不,我们可以直接用线段模拟这一过程。
$\quad\quad$ 最开始时,所有点都在同一个连通块内,表现在线段上,就是所有点都在连续的一条线段上。
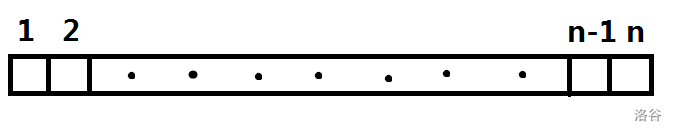
$\quad\quad$ 割断某一组割边后,原本的一个连通块会变成两个。我们把其中某一组连通块的点全部染成红色,另一组染成绿色。

$\quad\quad$ 我们不妨把所有涂成红色的点移到左边,把所有涂成绿色的点移到右边,变成这样:

$\quad\quad$ 这样一来,左边的所有点属于某一个连通块,右边的点属于另一个连通块,根据最小割树的构造原则,我们可以直接将左右两段递归处理,而不需要真的构图和分裂。
$\quad\quad$ 代码如下:
void build(int l, int r)
{
if(l == r) return ;
Dinic::S = pla[l], Dinic::E = pla[r];
int flow = Dinic::Dinic();
link[pla[l]].push_back(node(pla[r], flow));
link[pla[r]].push_back(node(pla[l], flow));
int L = l, R = r;
for(int k = l; k <= r; k++)
if(Dinic::deep[pla[k]] != 0x3f3f3f3f)
tem[L++] = pla[k];
else
tem[R--] = pla[k];
for(int k = l; k <= r; k++)
pla[k] = tem[k];
build(l, L - 1), build(L, r);
}
$\quad\quad$ 首先是变量的定义,$S,E,deep$是 Dinic 算法中的量,含义显然,$link$ 是最小割树上的边。
$\quad\quad$ 函数的两个参数 $l,r$ 代表当前处理的连通块在线段上的左右端点,$pla$ 代表在线段当前位置的节点的编号是多少(我们在线段上移动了节点,所以线段的 $i $ 位置并不一定是 $i$ 号点),$tem$ 是移动线段时的辅助数组。
$\quad\quad$ 分析代码:首先 if(l == r) return ; 代表递归的边界,即在线段左右端点重合(连通块内仅一个点)的时候跳出。
$\quad\quad$ Dinic::S = pla[l], Dinic::E = pla[r]; 代表从区间中选取两个点的过程,本质上任取两个不重复的点就可以了,这里取左右端点仅仅是为了方便。
$\quad\quad$ 下面这三句是算出最小割并往最小割树里加边的过程,不要忘了在每一次跑最大流之前还原每条边的流量。
int flow = Dinic::Dinic();
link[pla[l]].push_back(node(pla[r], flow));
link[pla[r]].push_back(node(pla[l], flow));
$\quad\quad$ 下面这一段是找出红绿两色点的过程,建立左右指针,红点插左指针,绿点插右指针,为了防止原数组被破坏,我们需要把它们插到一个辅助数组里,并在最后把辅助数组赋值给位置数组。
$\quad\quad$ 如何找出红绿两色点?在 Dinic 过程中,最后一次 bfs 触碰到的点的 $deep $ 不是初始值,而触碰到的点恰好是 $S$ 所在连通块内的点,可以看做同一种颜色,剩下的点自然是另一种颜色了。
int L = l, R = r;
for(int k = l; k <= r; k++)
if(Dinic::deep[pla[k]] != 0x3f3f3f3f)
tem[L++] = pla[k];
else
tem[R--] = pla[k];
for(int k = l; k <= r; k++)
pla[k] = tem[k];
$\quad\quad$ 最后递归下去就好了。
build(l, L - 1), build(L, r);
$\quad\quad$ 其它部分的代码难度不大,不过要注意细节。
#include <bits/stdc++.h>
using namespace std;
inline int read()
{
int x = 0, ch = '~';
while(!isdigit(ch)) ch = getchar();
while(isdigit(ch)) x = (x << 3) + (x << 1), x += ch - '0', ch = getchar();
return x;
}
const int N = 900 * 2;
const int M = 40000;
int n, m ;
namespace Dinic
{
int tot = 1, S, E, max_flow;
struct node
{
int to, flow;
} edge[M];
int ori_flow[M];
vector <int > link[N];
void add_edge(int u, int v, int w)
{
link[u].push_back(++tot), edge[tot].to = v, edge[tot].flow = w;
link[v].push_back(++tot), edge[tot].to = u, edge[tot].flow = w;
}
int deep[N], cur[N], vis[N];
queue <int > q;
bool bfs()
{
memset(cur, 0, sizeof(cur));
memset(vis, 0, sizeof(vis));
memset(deep, 0x3f, sizeof(deep));
q.push(S), vis[S] = 1, deep[S] = 0;
while(!q.empty())
{
int pla = q.front();
q.pop();
for(int k = 0; k < (int )link[pla].size(); k++)
{
int num = link[pla][k], to = edge[num].to;
if(!vis[to] && edge[num].flow)
vis[to] = 1, deep[to] = deep[pla] + 1, q.push(to);
}
}
return deep[E] != 0x3f3f3f3f;
}
int dfs(int pla, int flow)
{
if(pla == E)
{
max_flow += flow;
return flow;
}
int used = 0;
for(int k = cur[pla]; k < (int )link[pla].size(); k++, cur[pla] = k)
{
int num = link[pla][k], to = edge[num].to, Flow;
if(deep[to] == deep[pla] + 1 && edge[num].flow && (Flow = dfs(to, min(edge[num].flow, flow - used))))
edge[num].flow -= Flow, edge[num ^ 1].flow += Flow, used += Flow;
if(flow == used) break;
}
return used;
}
void init()
{
for(register int k = 2; k <= tot; k++)
ori_flow[k] = edge[k].flow;
}
int Dinic()
{
max_flow = 0;
for(register int k = 2; k <= tot; k++)
edge[k].flow = ori_flow[k];
while(bfs())
dfs(S, 0x3f3f3f3f);
return max_flow;
}
}
namespace GHT//Gomory_Hu_Tree
{
int pla[N], tem[N], deep[N];
int f[N][10], g[N][10];
struct node
{
int to, len;
node (int a, int b)
{
to = a, len = b;
}
node () { }
};
vector <node > link[N];
void build(int l, int r)
{
if(l == r) return ;
Dinic::S = pla[l], Dinic::E = pla[r];
int flow = Dinic::Dinic();
link[pla[l]].push_back(node(pla[r], flow));
link[pla[r]].push_back(node(pla[l], flow));
int L = l, R = r;
for(int k = l; k <= r; k++)
if(Dinic::deep[pla[k]] != 0x3f3f3f3f)
tem[L++] = pla[k];
else
tem[R--] = pla[k];
for(int k = l; k <= r; k++)
pla[k] = tem[k];
build(l, L - 1), build(L, r);
}
void dfs(int pla, int fa)
{
deep[pla] = deep[fa] + 1;
for(int k = 1; k < 10; k++) f[pla][k] = f[f[pla][k - 1]][k - 1];
for(int k = 1; k < 10; k++) g[pla][k] = min(g[pla][k - 1], g[f[pla][k - 1]][k - 1]);
for(int k = 0; k < (int )link[pla].size(); k++)
{
int to = link[pla][k].to;
int len = link[pla][k].len;
if(to != fa)
g[to][0] = len, f[to][0] = pla, dfs(to, pla);
}
}
int min(int u, int v)
{
int ans = 0x3f3f3f3f;
if(deep[u] < deep[v]) swap(u, v);
for(int k = 9; k >= 0; k--)
if(deep[u] - (1 << k) >= deep[v])
ans = std::min(ans, g[u][k]), u = f[u][k];
if(u == v) return ans;
for(int k = 9; k >= 0; k--)
if(f[u][k] != f[v][k])
ans = std::min(ans, g[u][k]), ans = std::min(ans, g[v][k]), u = f[u][k], v = f[v][k];
return std::min(std::min(ans, g[u][0]), g[v][0]);
}
}
int main()
{
memset(GHT::g, 0x3f, sizeof(GHT::g));
n = read() + 1, m = read();
for(register int k = 1; k <= m; k++)
{
int u = read(), v = read(), w = read();
Dinic::add_edge(u + 1, v + 1, w);
}
Dinic::init();
for(register int k = 1; k <= n; k++)
GHT::pla[k] = k;
GHT::build(1, n);
GHT::dfs(1, 0);
int Q = read();
for(register int k = 1; k <= Q; k++)
{
int u = read(), v = read();
printf("%d\n", GHT::min(u + 1, v + 1));
}
return 0;
}
$ $
$\quad\quad$ 例题:洛谷P4123 [CQOI2016]不同的最小割。
$\quad\quad$ 没啥好说的,因为只需要处理有多少种权值,甚至连最小割树都不需要建出来。
$\quad\quad$ 代码:
#include <bits/stdc++.h>
using namespace std;
inline int read()
{
int x = 0, ch = '~';
while(!isdigit(ch)) ch = getchar();
while(isdigit(ch)) x = (x << 3) + (x << 1), x += ch - '0', ch = getchar();
return x;
}
const int N = 900 * 2;
const int M = 40000;
int n, m ;
namespace Dinic
{
int tot = 1, S, E, max_flow;
struct node
{
int to, flow;
} edge[M];
int ori_flow[M];
vector <int > link[N];
void add_edge(int u, int v, int w)
{
link[u].push_back(++tot), edge[tot].to = v, edge[tot].flow = w;
link[v].push_back(++tot), edge[tot].to = u, edge[tot].flow = w;
}
int deep[N], cur[N], vis[N];
queue <int > q;
bool bfs()
{
memset(cur, 0, sizeof(cur));
memset(vis, 0, sizeof(vis));
memset(deep, 0x3f, sizeof(deep));
q.push(S), vis[S] = 1, deep[S] = 0;
while(!q.empty())
{
int pla = q.front();
q.pop();
for(int k = 0; k < (int )link[pla].size(); k++)
{
int num = link[pla][k], to = edge[num].to;
if(!vis[to] && edge[num].flow)
vis[to] = 1, deep[to] = deep[pla] + 1, q.push(to);
}
}
return deep[E] != 0x3f3f3f3f;
}
int dfs(int pla, int flow)
{
if(pla == E)
{
max_flow += flow;
return flow;
}
int used = 0;
for(int k = cur[pla]; k < (int )link[pla].size(); k++, cur[pla] = k)
{
int num = link[pla][k], to = edge[num].to, Flow;
if(deep[to] == deep[pla] + 1 && edge[num].flow && (Flow = dfs(to, min(edge[num].flow, flow - used))))
edge[num].flow -= Flow, edge[num ^ 1].flow += Flow, used += Flow;
if(flow == used) break;
}
return used;
}
void init()
{
for(register int k = 2; k <= tot; k++)
ori_flow[k] = edge[k].flow;
}
int Dinic()
{
max_flow = 0;
for(register int k = 2; k <= tot; k++)
edge[k].flow = ori_flow[k];
while(bfs())
dfs(S, 0x3f3f3f3f);
return max_flow;
}
}
set <int > s;
namespace GHT//Gomory_Hu_Tree
{
int pla[N], tem[N];
void build(int l, int r)
{
if(l == r) return ;
Dinic::S = pla[l], Dinic::E = pla[r];
int flow = Dinic::Dinic();
s.insert(flow);
int L = l, R = r;
for(int k = l; k <= r; k++)
if(Dinic::deep[pla[k]] != 0x3f3f3f3f)
tem[L++] = pla[k];
else
tem[R--] = pla[k];
for(int k = l; k <= r; k++)
pla[k] = tem[k];
build(l, L - 1), build(L, r);
}
}
int main()
{
n = read(), m = read();
for(register int k = 1; k <= m; k++)
{
int u = read(), v = read(), w = read();
Dinic::add_edge(u, v, w);
}
Dinic::init();
for(register int k = 1; k <= n; k++)
GHT::pla[k] = k;
GHT::build(1, n);
printf("%d", (int )s.size());
return 0;
}
$\quad\quad$ 练习:UVA11594 All Pairs Maximum Flow,代码就不放了,基本上还是模板。
$ $
结语:
$\quad\quad$ 最小割树的用处其实是不大的,但其算法的思想值得学习。
$\quad\quad$ 而且它是一个并不难,但是评级高的算法,黑模板题它的不香吗?
$\quad\quad$ 另外,证明过程并不保证正确(毕竟都是作者口胡出来的),若有误请联系作者Orz。
$ $
$$\large {E \ N \ D}$$


%%%