前言：

$ $

$\quad\quad$ 图片咕了可以去 洛谷博客 看。

$\quad\quad$ 最近复习了一下主席树，然后刷了刷主席树的训练场。

$\quad\quad$ 刷了第一题后发现不会做第二题：P3157 [CQOI2011]动态逆序对。

$\quad\quad$ 翻了翻题解，发现这题要求写一个带修的主席树…

$\quad\quad$ 看了半天，云里雾里，还以为是什么神奇的算法…

$\quad\quad$ 结果突然就发现：这玩意不是树套树么？

$\quad\quad$ AC 后写下本文加以巩固。

$ $

正文：

$ $

$\quad\quad$ 在介绍树状数组套动态开点线段树之前，我先大致提一提主席树。

$\quad\quad$ 主席树，顾名思义，就是某 hjt 提出的树。（雾

$\quad\quad$ 其学名为可持久化线段树，一般也可指动态开点线段树。

$\quad\quad$ 主要用来解决需要维护序列中某一段关于值的信息的题目。

$\quad\quad$ 什么叫 需要维护序列中某一段关于值的信息的题目 ？

$\quad\quad$ 众所周知，查询与值域有关的题目，有时可以用权值线段树解决。

$\quad\quad$ 比如说：查询整个序列中的 $\operatorname{Kth}$。

$\quad\quad$ 又众所周知：查询与原序列中的某个区间有关的题目，若是维护的数组具有可减性，就可以使前缀和解决。

$\quad\quad$ 比如说：查询区间 $[L,R]$ 内的所有数的和。

$\quad\quad$ 而把这两种题目合并起来，就成了 需要维护序列中某一段关于值的信息的题目 了。

$\quad\quad$ 比如说：查询区间 $[L,R]$ 内的 $\operatorname{Kth}$。

$\quad\quad$ 既然题目可以合并为一个，那么我们的算法是否也可以合并为一个？

$\quad\quad$ 答案是肯定的，我们可以开 $n$ 棵权值线段树，分别维护区间 $[1,1],[1,2],[1,3]......[1,n]$ 内的信息，查询时，我们利用信息的可减性即可求出答案。

$\quad\quad$ 但是 $\operatorname{Kth}$ 显然是不具有可减性的，所以我们不可能直接维护 $\operatorname{Kth}$。

$\quad\quad$ 我们可以维护 $size$（权值线段树中某一段区间内有多少个元素） 信息，而 $size$ 显然是具有可减性的。

$\quad\quad$ 这里举个栗子（黑色数字代表当前线段的维护值域区间，有颜色的数字代表当前区间的元素个数（size））：

$\quad\quad$ 我们提取出维护 $[1,L-1]$ 区间信息的权值线段树（假设是左边这颗），提取出维护 $[1,R]$ 区间信息的权值线段树（右边这棵）。

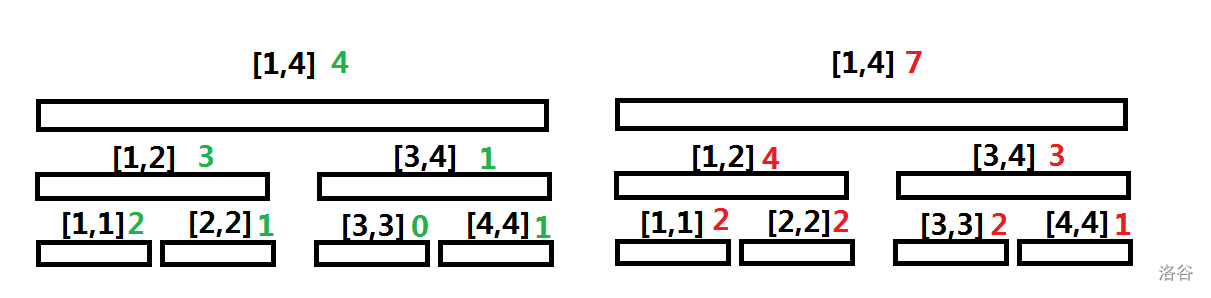
$\quad\quad$ 我们把这两颗线段树的每一个区间中 $size$ 的值对应相减，就得到了一颗维护 $[L,R]$ 区间信息的权值线段树。

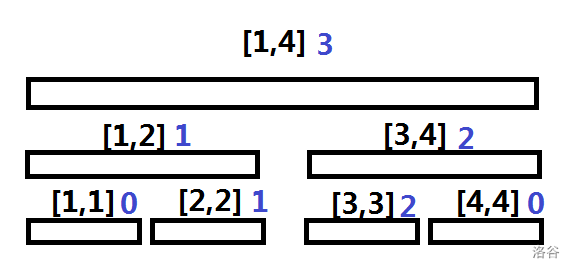
$\quad\quad$ 然后我们就可以在新的这颗线段树中简单的查找 $\operatorname {Kth}$了。

$\quad\quad$ 然而，虽然这个算法查询的时间复杂度是优秀的 $O(logn)$，但其空间复杂度以及建树时间复杂度达到了 $O(n^2)$（开了 $n$ 棵权值线段树），显然无法承受。

$\quad\quad$ 主席树就是在上面方法的基础上，对其空间复杂度进行优化而产生的数据结构。

$ $

$ $

$\quad\quad$ 如何优化空间复杂度？我们比较维护 $[1,x-1]$ 区间的权值线段树和维护 $[1,x]$ 区间的权值线段树（以下面两棵树为例，假设插入的值为 $1$）。

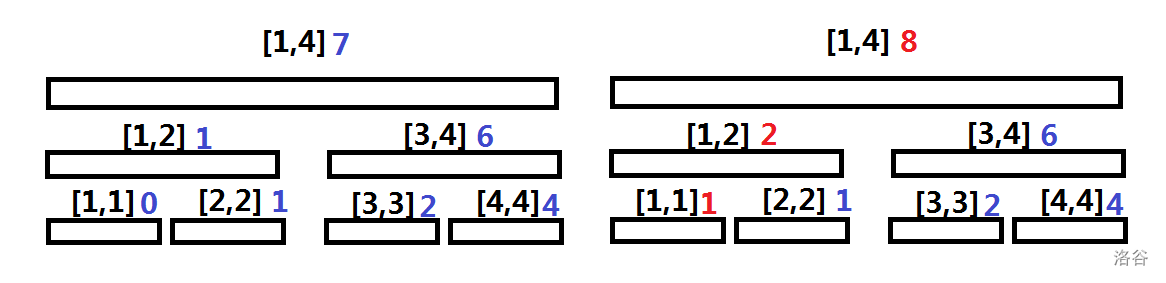
$\quad\quad$ 不难发现，插入新元素前的线段树与插入后的线段树仅仅只有一条链上的节点有区别，即 $logn$ 个节点有区别。

$\quad\quad$ 那我们为什么还要重复建立那些没有改变的节点？直接把原有树的该节点 “递” 给新树不就行了？

$\quad\quad$ 就像这样（绿色/棕红色的边代表线段树中的父子关系）：

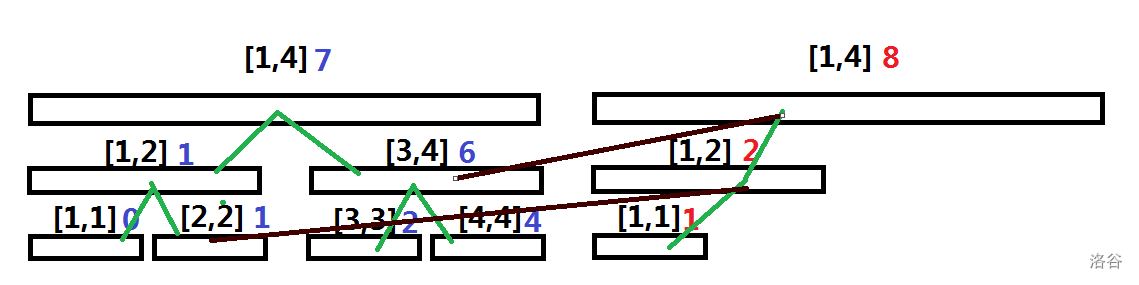
$\quad\quad$ 显然，这样操作后，任然可以从两颗线段树的根节点开始，顺着儿子访问这棵完整的线段树，但因为两棵树共用了一部分区域的关系，新建树的节点数仅仅只有改变了的 $logn$，因此，这样处理后，该数据结构的空间复杂度仅 $O(n+(n-1)logn)=O(nlogn)$。

$\quad\quad$ 这玩意就是所谓的主席树，即可持久化线段树。

$\quad\quad$ 为什么说它可持久化？因为如果我们对于任意的一次修改，新建修改路径上的所有节点，并按照上述方式建边，那么，我们就可以以 $O(nlogn)$ 的空间代价保存所有的历史状态，甚至回退到某一历史状态。

$\quad\quad$ 这里放一下板子和代码，然后就可以预备进入正题了。

$\quad\quad$ 板子：P3834 【模板】可持久化线段树 1（主席树）。

$\quad\quad$ 代码：

#include <bits/stdc++.h>

using namespace std;

inline int read()
{
    int x = 0, ch = '~';

    while(!isdigit(ch)) ch = getchar();
    while(isdigit(ch)) x = (x << 3) + (x << 1), x += ch - '0', ch = getchar();

    return x;
}

const int N = 200010;
const int M = N << 5;

int n, m, cnt, tot;
int d[N], ys[N], Root[N];
pair <int , int > a[N];

#define mid ((l+r)>>1)
#define ls (tree[root].lc)
#define rs (tree[root].rc)

struct node
{
    int lc, rc;
    int size;
} tree[M];

void creat(int & root, int l, int r)
{
    root = ++tot;
    if(l != r) creat(ls, l, mid), creat(rs, mid + 1, r);
}

int update(int pre, int l, int r, int x)
{
    int root = ++tot;

    ls = tree[pre].lc, rs = tree[pre].rc, tree[root].size = tree[pre].size + 1;

    if(l == r) return root;

    if(x <= mid) ls = update(tree[pre].lc, l, mid, x);
    else rs = update(tree[pre].rc, mid + 1, r, x);

    return root;
}

int Kth(int root1, int root2, int l, int r, int rank)
{
    if(l == r) return ys[l];

    int x = tree[tree[root2].lc].size - tree[tree[root1].lc].size;
    if(rank <= x) return Kth(tree[root1].lc, tree[root2].lc, l, mid, rank);
    else return Kth(tree[root1].rc, tree[root2].rc, mid + 1, r, rank - x);
}

int main()
{
    n = read(), m = read();
    for(register int k = 1; k <= n; k++)
        a[k] = make_pair(read(), k);

    sort(a + 1, a + 1 + n);
    for(register int k = 1; k <= n; k++)
    {
        if(a[k].first != a[k - 1].first || k == 1)
            ys[++cnt] = a[k].first;
        d[a[k].second] = cnt;
    }

    creat(Root[0], 1, cnt);
    for(register int k = 1; k <= n; k++)
        Root[k] = update(Root[k - 1], 1, cnt, d[k]);

    for(register int k = 1; k <= m; k++)
    {
        int l = read(), r = read(), x = read();
        printf("%d\n", Kth(Root[l - 1], Root[r], 1, cnt, x));
    }

    return 0;
}

$ $

$ $

$ $

$\quad\quad$ 下面进入正题。

$\quad\quad$ 我们知道，静态区间 $\operatorname{Kth}$ 可以用主席树维护解决，那么动态的区间 $\operatorname{Kth}$ 怎么解决呢？

$\quad\quad$ 比如说这道题：P2617 Dynamic Rankings。

$\quad\quad$ 题意很简单：维护一种数据结构，支持单点修改，区间 $\operatorname{Kth}$。

$\quad\quad$ 能否直接上主席树暴力修改？

$\quad\quad$ 众所周知，主席树本质上维护的是前缀和信息，如果我们要修改 $i$ 处的点值，我们就要修改 $i - n$ 中每一棵权值线段树内的信息，而每一棵权值线段树都有 $log$ 个节点需要修改，所以我们单次修改的复杂度会达到恐怖的 $O(nlogn)$。

$\quad\quad$ 当然，我们在主席树中是共用了一些点的，所以对于某些点的修改可能会重复，我们可以把那些已修改的节点打上标记，再次访问到它的时候就不用修改了。

$\quad\quad$ 这似乎可以降低暴力修改的时间复杂度，但因为 $n$ 棵树中，每一棵树的根节点都是新建的，而我们对于每一棵树的修改一定会从根节点开始，所以我们每次修改都会至少修改 $n$ 个节点（各棵树的根节点），单次修改复杂度下界也还是 $O(n)$。

$\quad\quad$ 因此，暴力不可接受。

$\quad\quad$ 如何对暴力进行优化？我们把问题简化考虑。

$\quad\quad$ 假设我们要维护的信息与值域无关，也就是说我们不用维护权值线段树，那么我们应该怎么做？

$\quad\quad$ 比如说题目简化为这样：维护一种数据结构，支持单点修改，区间 $\operatorname{Sum}$。

$\quad\quad$ 我们原先的暴力主席树，类比过来就相当于跑了一个前缀和。

$\quad\quad$ 但是单点修改区间求值为啥要跑前缀和？树状数组跑一下不就完了吗？

$\quad\quad$ 使用树状数组，显然可以把前缀和的 $O(n)$ 修改， $O(1)$ 查询优化到 $O(logn)$ 修改和查询。

$\quad\quad$ 对于更复杂一些的本题是否也是如此？

$\quad\quad$ 如果用树状数组代替前缀和维护权值线段树（主席树本质上就是用前缀和维护权值线段树），我们是否可以把之前的 $O(nlogn)$ 修改，$O(logn)$ 查询，优化到 $O(nlog^2n)$ 修改和查询？

$\quad\quad$ 显然是可以的。

$\quad\quad$ 具体而言如何实现？

$\quad\quad$ 我们考虑树状数组是怎么实现单点修改，区间查询的（下面介绍的很简略，但要是你连树状数组都不会，你看树套树干嘛）：

$\quad\quad$ 树状数组构造时，建立了 $n$ 个节点，分别维护$[1,1],[1,2],[3,3],[1,4]…[n-lowbit(n)+1,n]$ 区间内信息。

$\quad\quad$ 修改时，修改 $x,x+lowbit(x)......$ 等节点，直到达到 $n$ 之外。

$\quad\quad$ 查询时，分别查询 $[1,l-1]$ 和 $[1,r]$ 内的信息，然后相减。

$\quad\quad$ 类比到树套树上，就是构造 $n$ 棵权值线段树，分别维护 $[1,1],[1,2],[3,3],[1,4]…[n-lowbit(n)+1,n]$ 区间内信息。

$\quad\quad$ 修改时，修改以 $x,x+lowbit(x)......$ 等节点为根的权值线段树，直到达到 $n$ 之外。

$\quad\quad$ 查询时，分别构造 $[1,l-1]$ 和 $[1,r]$ 的权值线段树，然后相减得到 $[l,r]$ 的权值线段树。

$\quad\quad$ 其实，这里的操作只不过是把树状数组中的 “节点” 换成了 “权值线段树” 而已，了解思路之后自己就可以口胡出来。

$\quad\quad$ 下面放一下上面那例题 P2617 Dynamic Rankings 的代码：

#include <bits/stdc++.h>
#define lowbit(x) (x&(-x))

using namespace std;

inline int read()
{
    int x = 0, ch = '~', fh = 1;

    while(!isdigit(ch)) fh = ch == '-' ? -1 : 1, ch = getchar();
    while(isdigit(ch)) x = (x << 3) + (x << 1), x += ch - '0', ch = getchar();

    return x * fh;
}

const int N = 200010;

int a[N], ys[N], Root[N];
int n, m , num, tot, cnt;

struct Node
{
    int opt, a, b, c;
} ques[N];
struct NODE
{
    int type, wz, key;

    bool operator < (const NODE & other) const
    {
        return key < other.key;
    }
} cl[N * 2];

struct node
{
    int lc, rc, size;
} tree[N << 6];

#define mid ((l+r)>>1)
#define ls (tree[root].lc)
#define rs (tree[root].rc)

void update(int & root, int l, int r, int key, int val)
{
    if(!root) root = ++tot;
    tree[root].size += val;

    if(l == r) return ;
    if(key <= mid) update(ls, l, mid, key, val);
    else update(rs, mid + 1, r, key, val);
}

void Change(int wz, int key, int val)
{
    for(int k = wz; k <= n; k += lowbit(k))
        update(Root[k], 1, cnt, key, val);
}

vector <int > L, R;

int query(int l, int r, int Kth)
{
    if(l == r) return ys[l];

    int l_sum = 0, r_sum = 0;
    for(int k = 0; k < (int )L.size(); k++) l_sum += tree[tree[L[k]].lc].size;
    for(int k = 0; k < (int )R.size(); k++) r_sum += tree[tree[R[k]].lc].size;

    int Size = r_sum - l_sum;
    if(Kth <= Size)
    {
        for(int k = 0; k < (int )L.size(); k++) L[k] = tree[L[k]].lc;
        for(int k = 0; k < (int )R.size(); k++) R[k] = tree[R[k]].lc;
        return query(l, mid, Kth);
    }
    else
    {
        for(int k = 0; k < (int )L.size(); k++) L[k] = tree[L[k]].rc;
        for(int k = 0; k < (int )R.size(); k++) R[k] = tree[R[k]].rc;
        return query(mid + 1, r, Kth - Size);
    }
}

int Query(int l, int r, int Kth)
{
    L.clear(), R.clear();
    for(int k = l; k > 0; k -= lowbit(k)) L.push_back(Root[k]);
    for(int k = r; k > 0; k -= lowbit(k)) R.push_back(Root[k]);
    return query(1, cnt, Kth);
}

int main()
{
    n = read(), m = read();
    for(register int k = 1; k <= n; k++)
        a[k] = read(), cl[++num].type = 1, cl[num].wz = k, cl[num].key = a[k];
    for(register int k = 1; k <= m; k++)
    {
        char opt[2];
        scanf("%s", opt);

        if(opt[0] == 'Q') ques[k].opt = 0, ques[k].a = read(), ques[k].b = read(), ques[k].c = read();
        else
        {
            ques[k].opt = 1, ques[k].a = read(), ques[k].b = read();
            cl[++num].type = 2, cl[num].wz = k, cl[num].key = ques[k].b;
        }
    }

    sort(cl + 1, cl + 1 + num);
    int last = 0xefefefef;
    for(register int k = 1; k <= num; k++)
    {
        if(cl[k].key != last)
            last = cl[k].key, cnt++, ys[cnt] = cl[k].key;
        if(cl[k].type == 1) a[cl[k].wz] = cnt;
        else ques[cl[k].wz].b = cnt;
    }

    for(register int k = 1; k <= n; k++)
        Change(k, a[k], 1);

    for(register int k = 1; k <= m; k++)
    {
        if(ques[k].opt)
        {
            Change(ques[k].a, a[ques[k].a], -1);
            a[ques[k].a] = ques[k].b;
            Change(ques[k].a, a[ques[k].a], 1);
        }
        else
            printf("%d\n", Query(ques[k].a - 1, ques[k].b, ques[k].c));
    }

    return 0;
}

$\quad\quad$ 上面提到，主席树是用来解决需要维护序列中某一段关于值的信息的题目的东西。

$\quad\quad$ 而树状数组套动态开点线段树就是用来解决需要维护序列中某一段关于值的信息并支持修改的题目的东西了。

$\quad\quad$ （有的人说这是树状数组套主席树，我觉得这么说是很不科学的，毕竟主席树本身就是用前缀和维护的权值线段树，而这里是用树状数组维护权值线段树，把它称作树状数组套线段树才对吧，或者说是带修主席树也说得过去......不过话说回来，主席树 到底是指啥，本身也是有争议的吧，要是把它理解为动态开点线段树，貌似说这个树套树是树状数组套主席树也没错）

$\quad\quad$ 再一道练习：P3157 [CQOI2011]动态逆序对

$\quad\quad$ 代码：

#include <bits/stdc++.h>

using namespace std;

const int N = 200010;

inline int read()
{
    int x = 0, ch = '~', fh = 1;

    while(!isdigit(ch)) fh = ch == '-' ? -1 : 1, ch = getchar();
    while(isdigit(ch)) x = (x << 3) + (x << 1), x += ch - '0', ch = getchar();

    return x * fh;
}

long long ans;
int n, m, tot;
int a[N], wz[N], Root[N];

struct node
{
    int lc, rc, size;
} tree[N << 6];

#define ls (tree[root].lc)
#define rs (tree[root].rc)
#define mid ((l + r) >> 1)
#define lowbit(x) (x & (-x))

void update(int & root, int l, int r, int key, int val)
{
    if(!root) root = ++tot;
    tree[root].size += val;

    if(l == r) return ;
    if(key <= mid) update(ls, l, mid, key, val);
    else update(rs, mid + 1, r, key, val);
}

void Change(int wz, int key, int val)
{
    for(int k = wz; k <= n; k += lowbit(k))
        update(Root[k], 1, n, key, val);
}

vector <int > L, R;

int query(int l, int r, int x)
{
    if(x <= mid)
    {
        if(l == r) return 0;

        for(int k = 0; k < (int )L.size(); k++) L[k] = tree[L[k]].lc;
        for(int k = 0; k < (int )R.size(); k++) R[k] = tree[R[k]].lc;
        return query(l, mid, x);
    }
    if(l == r)
    {
        int l_size = 0, r_size = 0;
        for(int k = 0; k < (int )L.size(); k++) l_size += tree[L[k]].size;
        for(int k = 0; k < (int )R.size(); k++) r_size += tree[R[k]].size;
        return r_size - l_size;
    }

    int l_size = 0, r_size = 0;
    for(int k = 0; k < (int )L.size(); k++) l_size += tree[tree[L[k]].lc].size;
    for(int k = 0; k < (int )R.size(); k++) r_size += tree[tree[R[k]].lc].size;
    for(int k = 0; k < (int )L.size(); k++) L[k] = tree[L[k]].rc;
    for(int k = 0; k < (int )R.size(); k++) R[k] = tree[R[k]].rc;
    return r_size - l_size + query(mid + 1, r, x);
}

int Query(int l, int r, int x)
{
    L.clear(), R.clear();
    for(int k = l; k > 0; k -= lowbit(k)) L.push_back(Root[k]);
    for(int k = r; k > 0; k -= lowbit(k)) R.push_back(Root[k]);
    return query(1, n, x);
}

signed main()
{
    n = read(), m = read();
    for(register int k = 1; k <= n; k++)
    {
        a[k] = read(), wz[a[k]] = k;
        if(k > 1) ans += k - 1 - Query(0, k - 1, a[k]);
        Change(k, a[k], 1);
    }

    for(register int k = 1; k <= m; k++)
    {
        printf("%lld\n", ans);

        int x = read();
        Change(wz[x], x, -1);
        ans -= Query(wz[x], n, x);
        ans -= Query(0, wz[x] - 1, 0x3f3f3f3f) - Query(0, wz[x] - 1, x);
    }

    return 0;
}

$ $

结语：

$\quad\quad$ 个人感觉树套树的结构并没有什么条条框框，大多数时候都是靠自己口胡来着。

$\quad\quad$ 到这里还记模板貌似没啥大用啊…要是你记了个树状数组套动态开点线段树，哪天考一个线段树套平衡树，那不就 GG 了么......

$ $