1) 数位dp
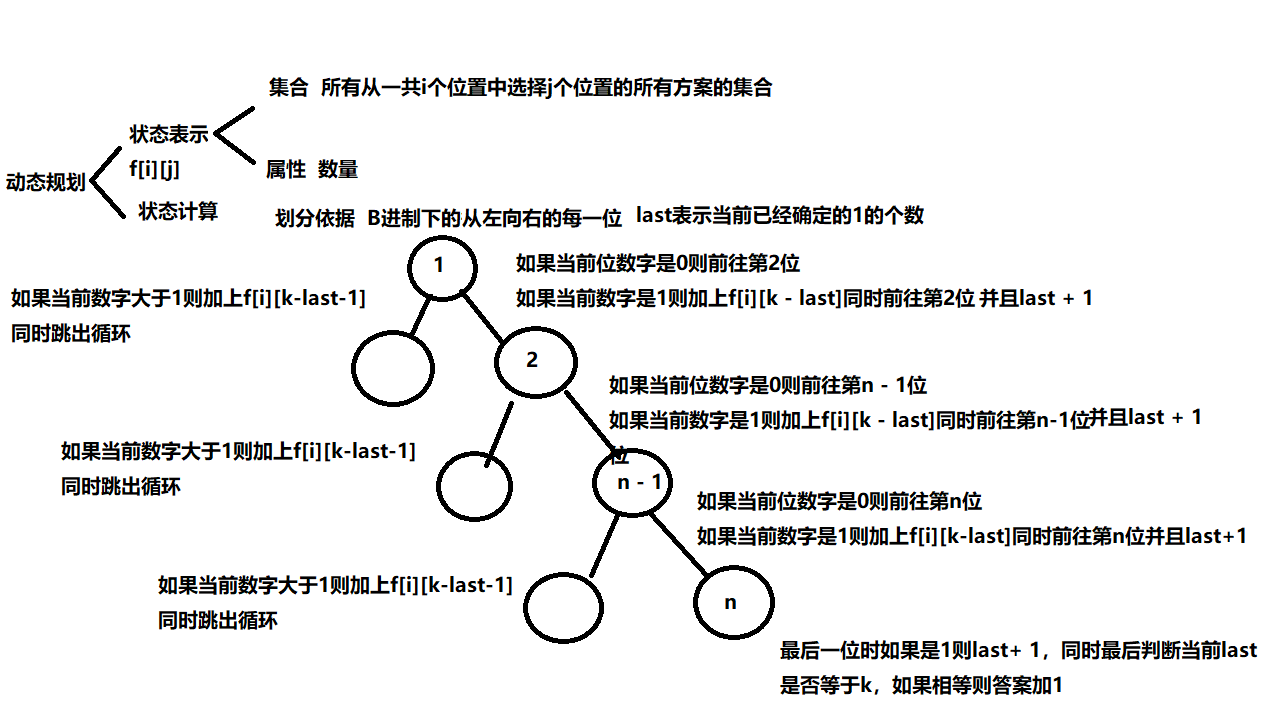
本题的 F[i][j] 数组表示在 i 个位置中选择 j 个位置填上 1 的所有方案的数量
last 表示当前已经确定的 1 的个数
$$ F[i][j] = F[i - 1][j] + F[i - 1][j - 1] $$


#include<iostream>
#include<cstring>
#include<cstdio>
#include<algorithm>
#include<vector>
using namespace std;
const int N = 35;
int f[N][N], K, B, l, r;
void init()
{
for(int i = 0; i < N; i ++)
for(int j = 0; j <= i; j ++)
if(!j) f[i][j] = 1;
else f[i][j] = f[i - 1][j] + f[i - 1][j - 1];
}
int dp(int n)
{
if(!n) return 0;
vector < int > nums;
while(n) nums.push_back(n % B), n /= B;
// for(int i = nums.size() - 1; i >= 0; i --) cout << nums[i] << " ";
// cout << endl;
int res = 0;
int last = 0;
for(int i = nums.size() - 1; i >= 0; i --){
int x = nums[i];
if(x){// 如果当前数大于0,也就是后面的位数可以全取1
res += f[i][K - last];// 当前位取0,也就是后面的i位数加一个组合计数
if(x > 1){// 当前位的数大于1,也就是当前位加后面的i位数都可以取1
if(K - last - 1 >= 0) res += f[i][K - last - 1];// 加上当前位取1的组合计数
break;
}else{// 当前位是1,后面的i位的数字大小无法确定,也就不是组合计数
last ++;// 但已经可以确定数是1
if(last > K) break;
}
}
if(!i && last == K) res ++;
}
return res;
}
int main()
{
cin >> l >> r >> K >> B;
init();
// for(int i = l; i <= r; i ++)
// dp(i);
cout << dp(r) - dp(l - 1) << endl;
return 0;
}
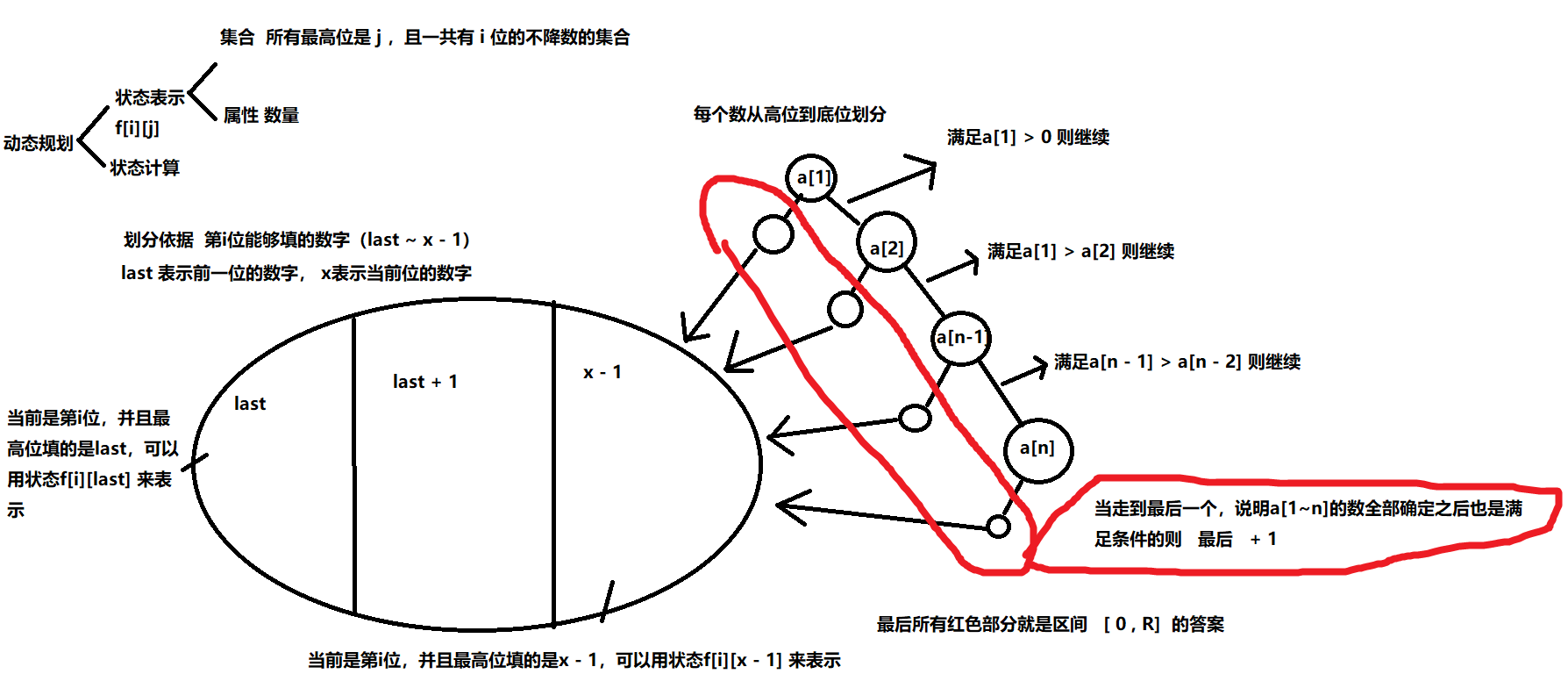
首先题目要求的是从左到右各位数字呈非下降关系,如 123,446。
然后题目要求的是一段区间[L,R]中的数量
所以还是可以用前缀和的思想,先求出[0,L-1] 和 [0,R]两个区间的数量然后区间[0,R] - 区间[0,L-1]就是答案
然后就是本题的 F[i][j] 数组表示的是一共有 i 位数字,并且最高位是 j 的所有数的集合
last 表示当前遍历到第 i 位, last就是第 i - 1 位的数字大小
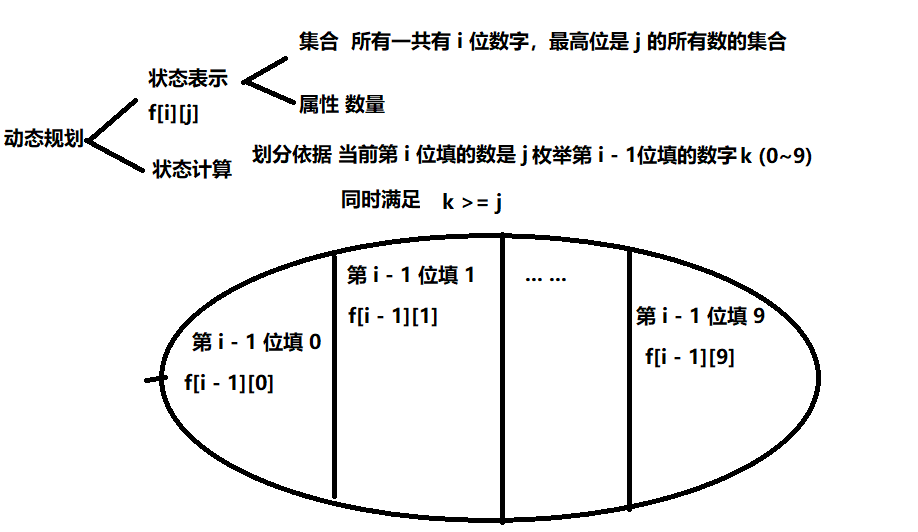
$$
F[i][j] = \sum_{k=0}^{9}{F[i - 1][k]} (k>=j)
$$

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<vector>
using namespace std;
const int N = 15;
int f[N][N], l, r;
void init()
{
for(int i = 0; i <= 9; i ++) f[1][i] = 1;
for(int i = 2; i < N; i ++)
for(int j = 0; j <= 9; j ++)
for(int k = j; k <= 9; k ++)
f[i][j] += f[i - 1][k];
}
int dp(int n)
{
if(!n) return 1;
vector < int > num;
while(n) num.push_back(n % 10), n /= 10;
int res = 0, last = 0;
for(int i = num.size() - 1; i >= 0; i --){// 遍历每一位(树一样的那部分)
int x = num[i];
for(int j = last; j < x; j ++)// 集合的划分部分
res += f[i + 1][j];
if(last > x) break;// 判断是否继续
last = x;// 计算完当前位,将当前位的数赋值给last,
if(!i) res ++;// 判断是否进行到最后一位
}
return res;
}
int main()
{
init();
while(cin >> l >> r) cout << dp(r) - dp(l - 1) << endl;
return 0;
}
首先题目要求的是不含前导零且相邻两个数字之差至少为 2 的正整数 比如 25 26 31 135
然后题目要求的是一段区间[L,R]中的数量
所以还是可以用前缀和的思想,先求出[0,L-1] 和 [0,R]两个区间的数量然后区间[0,R] - 区间[0,L-1]就是答案
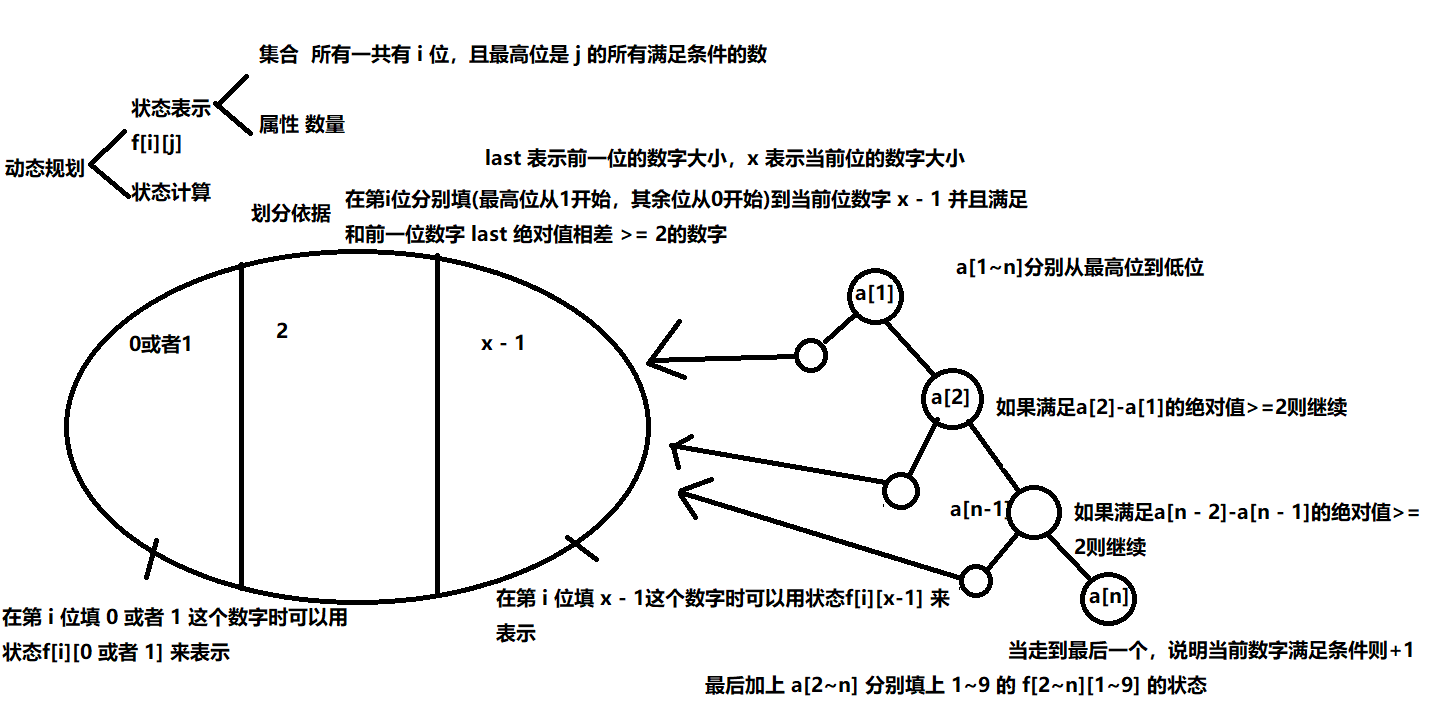
然后就是本题的 F[i][j] 数组表示的是一共有 i 位数字,并且最高位是 j 的所有数的集合
last 表示当前遍历到第 i 位, last就是第 i - 1 位的数字大小
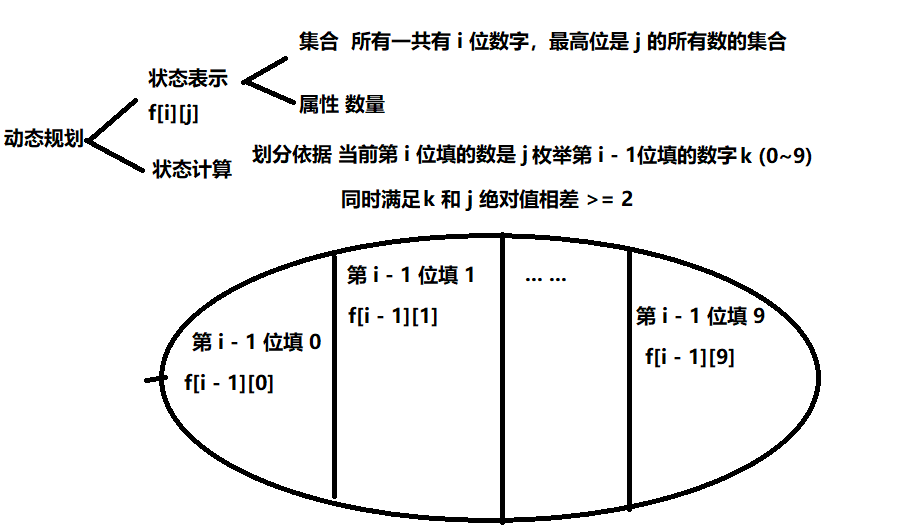
$$
F[i][j] = \sum_{k = 0}^{9} F[i - 1][k] (|k - j| >= 2)
$$
然后这个就是有一个前导0需要注意的,也就是我们不能够在最高位填0这个数字
比如 321 我们不能在 3 这个位置填上 0 因为根据f[i][j]数组的定义这个地方填 0 会丢失 013 014 等等很多数据
所以我们需要单独的处理前导 0 这个问题,就是在除最高位的所有其他位置可以分别填上 1~9
上面那个题目(数字游戏)可以包含前导 0
比如 321 在最高位 3 上填 0 依然不会丢失 003 012(这样也是满足条件) 这样的数据
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<vector>
using namespace std;
const int N = 15;
int f[N][N], l, r;
void init()
{
for(int i = 0; i <= 9; i ++) f[1][i] = 1;
for(int i = 2; i < N; i ++)
for(int j = 0; j <= 9; j ++)
for(int k = 0; k <= 9; k ++)
if(abs(k - j) >= 2)
f[i][j] += f[i - 1][k];
}
int dp(int n)
{
if(!n) return 0;
vector < int > nums;
while(n) nums.push_back(n % 10), n /= 10;
int res = 0, last = -2;
for(int i = nums.size() - 1; i >= 0; i --){
int x = nums[i];
for(int j = i == nums.size() - 1; j < x; j ++)// 集合划分从 0(1) 到 x - 1
if(abs(last - j) >= 2)
res += f[i + 1][j];
if(abs(last - x) < 2) break;// 判断是否满足条件
last = x;
if(!i) res ++;// 遍历到最后一位
}
for(int i = 1; i < nums.size(); i ++)// 最高位取0时的情况
for(int j = 1; j <= 9; j ++)
res += f[i][j];
return res;
}
int main()
{
init();
cin >> l >> r;
cout << dp(r) - dp(l - 1) << endl;
return 0;
}
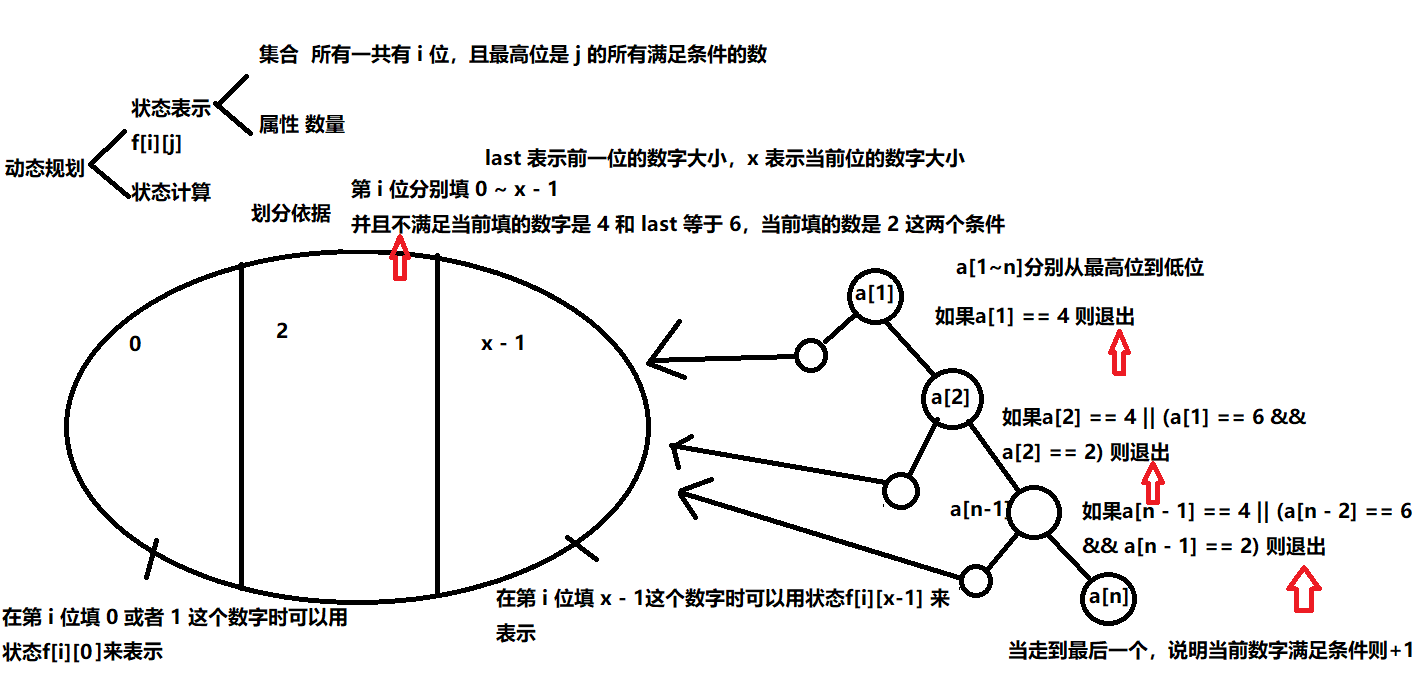
首先题目要求的是数字中不包含4且不包含连续的62的数字 比如24 162都是不满足条件的
然后题目要求的是一段区间[L,R]中的数量
所以还是可以用前缀和的思想,先求出[0,L-1] 和 [0,R]两个区间的数量然后区间[0,R] - 区间[0,L-1]就是答案
然后就是本题的 F[i][j] 数组表示的是一共有 i 位数字,并且最高位是 j 的所有数的集合
last 表示当前遍历到第 i 位, last就是第 i - 1 位的数字大小
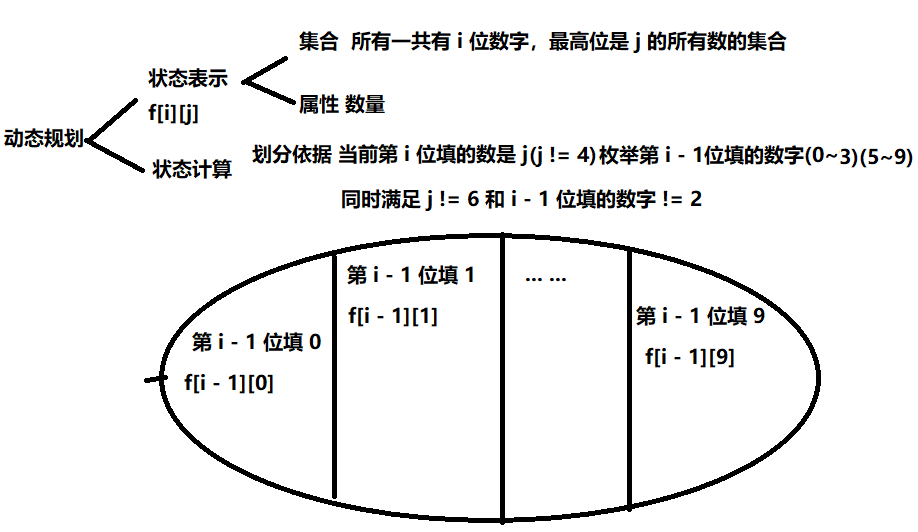
$$
F[i][j] = \sum_{k=0}^{9} F[i - 1][k] (j != 4)(k != 4)(j != 6 同时 k != 2)
$$
然后这个题目时可以填上前导0的,因为 023 是满足条件的
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<vector>
using namespace std;
const int N = 15;
int f[N][N], l, r;
void init()
{
for(int i = 0; i <= 9; i ++){
if(i == 4) continue;
f[1][i] = 1;
}
for(int i = 2; i < N; i ++)
for(int j = 0; j <= 9; j ++){
if(j == 4) continue;
for(int k = 0; k <= 9; k ++){
if(k == 4 || (j == 6 && k == 2)) continue;
f[i][j] += f[i - 1][k];
}
}
}
int dp(int n)
{
if(!n) return 1;
vector < int > nums;
while(n) nums.push_back(n % 10), n /= 10;
int res = 0, last = 0;
for(int i = nums.size() - 1; i >= 0; i --){// 遍历每一位
int x = nums[i];
for(int j = 0; j < x; j ++){ // 集合划分的部分
if(j == 4 || (last == 6 && j == 2)) continue;
res += f[i + 1][j];
}
if(x == 4 || (last == 6 && x == 2)) break;// 如果出现4 或者连续的62则退出
last = x;// last 表示前一位的数字
if(!i) res ++;
}
return res;
}
int main()
{
init();
while(cin >> l >> r , l || r)
cout << dp(r) - dp(l - 1) << endl;
return 0;
}
首先题目要求的是一个数中每个数字加起来模 N 等于 0 的数 比如 N = 9 时,9,18,27 都是满足条件的
然后题目要求的是一段区间[L,R]中的数量
所以还是可以用前缀和的思想,先求出[0,L-1] 和 [0,R]两个区间的数量然后区间[0,R] - 区间[0,L-1]就是答案
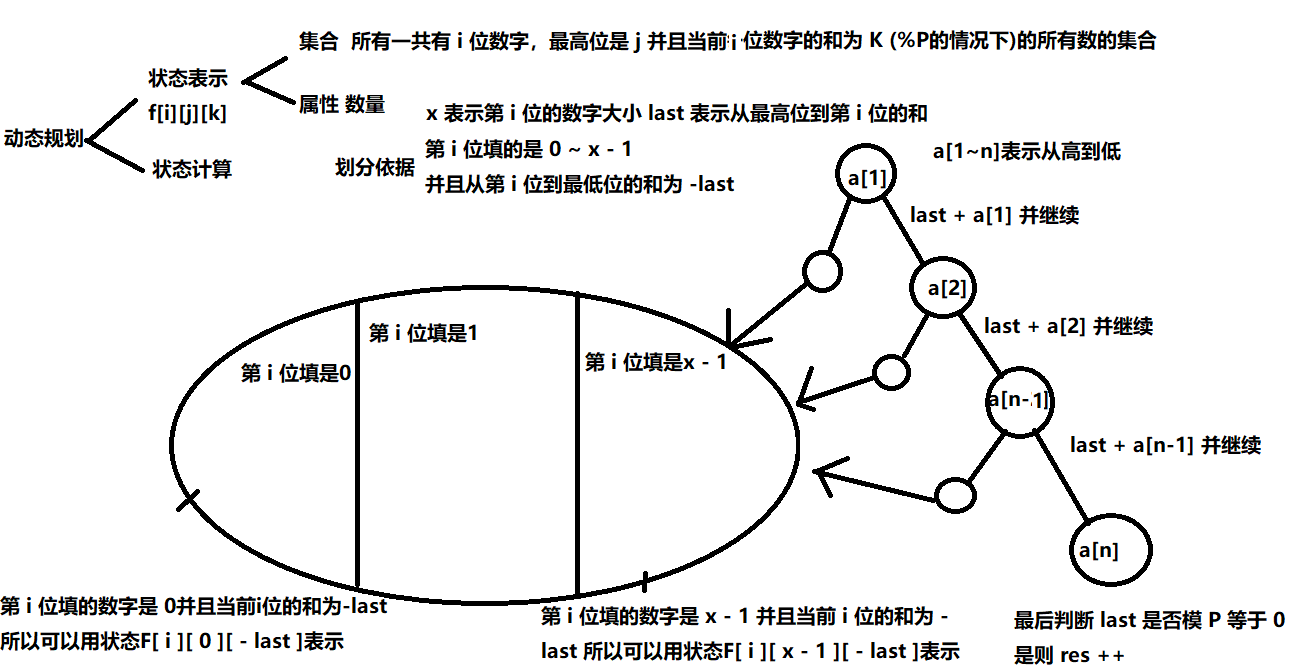
然后就是本题的 F[i][j][k] 数组表示的是一共有 i 位数字,最高位是 j 并且当前 i 位数字的和为 K (%P的情况下)的所有数的集合
last 表示当前遍历到第 i 位, last就是前 i - 1 位的数字的和
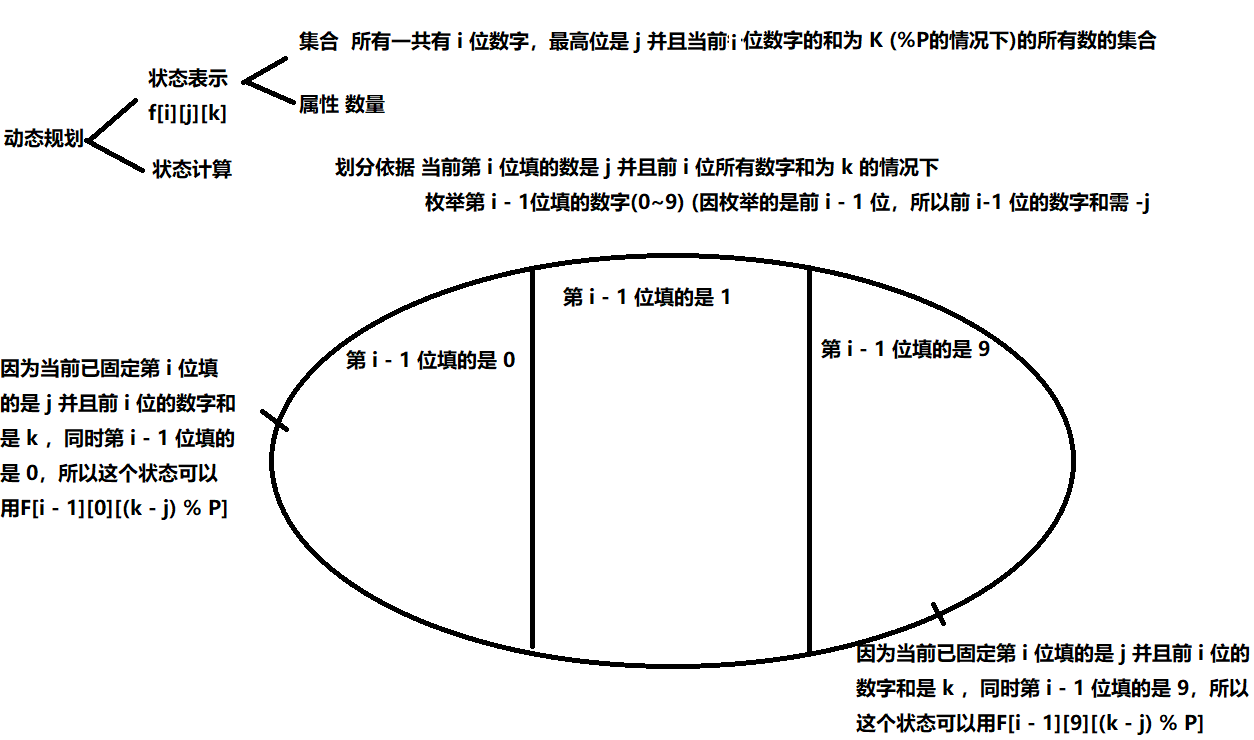
$$
F[i][j][k] = \sum_{x=0}^{9} F[i - 1][x][(k - j) \% P] (0 <= j <= 9) (0 <= k < P)
$$
首先就是 a + b ≡ 0(mod N),同余等式两边是可以移项的,所以就有 a ≡ −b(mod N)。
然后就是从高到低枚举每一位时
当我在第 i 位填数字时,如何才能保证我们填上数字之后,所有的数字之和加起来(此时并不确定后面填的啥数字) % P == 0
这个时候 last(表示当前遍历到第 i 位,last就是前 i - 1 位的数字的和)就能用上,首先我们假设第 i 位到最低位的和是 X
此时的 last + x 就是所有位的数字和
然后就是 last + x ≡ 0(mod P),同余等式两边是可以移项的,所以就有 x ≡ −last(mod P)。
此时我们就可以用 -last 来表示 x (此时我们不确定后面填的啥数字,但我们确定了后面填的数字的和)
也即我们就可以用我们的状态 F[ i ][ j ][ - last ] 一共有 i 位数字,最高位是 j 并且当前 i 位数字的和为 -last (%P的情况下)的所有数的集合
#include<iostream>
#include<cstring>
#include<cstdio>
#include<algorithm>
#include<vector>
using namespace std;
const int N = 15, M = 110;
int f[N][N][M], l, r, p;
int mod(int x, int y)
{
return ((x % y) + y) % y;
}
void init()
{
memset(f, 0, sizeof f);
for(int i = 0; i <= 9; i ++) f[1][i][i % p] ++;
for(int i = 2; i < N; i ++)
for(int j = 0; j <= 9; j ++)
for(int k = 0; k < p; k ++)
for(int x = 0; x <= 9; x ++)
f[i][j][k] += f[i - 1][x][mod(k - j, p)];
}
int dp(int n)
{
if(!n) return 1;
vector < int > nums;
while(n) nums.push_back(n % 10), n /= 10;
int res = 0, last = 0;
for(int i = nums.size() - 1; i >= 0; i --){
int x = nums[i];
for(int j = 0; j < x; j ++)
res += f[i + 1][j][mod(-last, p)];
last += x;
if(!i && (last % p == 0)) res ++;
}
return res;
}
int main()
{
while(cin >> l >> r >> p){
init();
cout << dp(r) - dp(l - 1) << endl;
}
return 0;
}
emmm… 下次补把


tql