A. Add Odd or Subtract Even
You are given two positive integers $a$ and $b$.
In one move, you can change $a$ in the following way:
- Choose any positive odd integer $x(x > 0)$ and replace a with $a + x$;
- choose any positive even integer $y(y > 0)$ and replace a with $a − y$.
You can perform as many such operations as you want. You can choose the same numbers $x$ and $y$ in different moves.
Your task is to find the minimum number of moves required to obtain $b$ from $a$. It is guaranteed that you can always obtain $b$ from $a$.
You have to answer $t$ independent test cases.
Input
The first line of the input contains one integer $t(1$ $\leq$ $t$ $\leq$ $10^4)$ — the number of test cases.
Then $t$ test cases follow. Each test case is given as two space-separated integers $a$ and $b(1$ $\leq$ $a, b$ $\leq$ $10^9)$.
Output
For each test case, print the answer — the minimum number of moves required to obtain $b$ from $a$ if you can perform any number of moves described in the problem statement. It is guaranteed that you can always obtain $b$ from $a$.
Example
input
5
2 3
10 10
2 4
7 4
9 3
output
1
0
2
2
1
Note
In the first test case, you can just add $1$.
In the second test case, you don’t need to do anything.
In the third test case, you can add $1$ two times.
In the fourth test case, you can subtract $4$ and add $1$.
In the fifth test case, you can just subtract $6$.
题解
用小学知识可以知道,一个奇数如果加上一个奇数它会变成一个偶数,一个奇数如果加上一个偶数它依然是一个奇数;一个偶数如果加上一个奇数它会变成奇数,一个偶数如果加上一个偶数它依然是偶数;减法同理。
因此,当输入的 $a > b$ 的时候,将 $a$ 变成 $b$ 必须要做减法,而题目规定被减数只能是偶数,此时,若 $a, b$ 的差为偶数,则只需要做一次操作,直接减去这个差值,就可以使得 $a = b$;若很不幸 $a, b$ 的差为奇数,又因为奇数加奇数会变成一个偶数,所以此时可以简单考虑为,先减去 $(差值 + 1)$,此时 $a = b - 1$,只需要再把这个 $1$ 加回来即可,而题目规定加法操作正好可以加一个奇数,至此操作了 $2$ 次,不难发现当 $a > b$ 的时候,分成这两种情况讨论就可以得到答案,若 $a < b$ 时也同理可得到类似的结论,当然,如果输入的两个数已经相等,就不需要做任何操作。
代码如下,也就是简单的 if else 判断语句的操作。
# include <iostream>
using namespace std;
int main()
{
int T;
cin >> T;
while (T--) {
int a, b;
cin >> a >> b;
if (a == b)
cout << 0 << endl;
else if (a > b)
if (a - b & 1)
cout << 2 << endl;
else
cout << 1 << endl;
else
if (b - a & 1)
cout << 1 << endl;
else
cout << 2 << endl;
}
return 0;
}
B. WeirdSort
You are given an array $a$ of length $n$.
You are also given a set of distinct positions $p_1, p_2, … , p_m$, where $1 \leq p_i < n$. The position $p_i$ means that you can swap elements $a[p_i]$ and $a[p_i + 1]$. You can apply this operation any number of times for each of the given positions.
Your task is to determine if it is possible to sort the initial array in non-decreasing order $(a_1 \leq a_2 \leq … \leq a_n)$ using only allowed swaps.
For example, if $a=[3,2,1]$ and $p=[1,2]$, then we can first swap elements $a[2]$ and $a[3]$ $($because position $2$ is contained in the given set $p)$. We get the array $a=[3,1,2]$. Then we swap $a[1]$ and $a[2]$ $($position $1$ is also contained in $p)$. We get the array $a=[1,3,2]$. Finally, we swap $a[2]$ and $a[3]$ again and get the array $a=[1,2,3]$, sorted in non-decreasing order.
You can see that if $a=[4,1,2,3]$ and $p=[3,2]$ then you cannot sort the array.
You have to answer $t$ independent test cases.
Input
The first line of the input contains one integer $t (1 \leq t \leq 100)$ — the number of test cases.
Then $t$ test cases follow. The first line of each test case contains two integers $n$ and $m$ $(1 \leq m < n \leq 100)$ — the number of elements in $a$ and the number of elements in $p$. The second line of the test case contains $n$ integers $a_1, a_2, …, a_n (1 \leq a_i \leq 100)$. The third line of the test case contains $m$ integers $p_1, p_2, …, p_m (1 \leq p_i < n$, all $p_i$ are distinct$)$ — the set of positions described in the problem statement.
Output
For each test case, print the answer — “$YES$” (without quotes) if you can sort the initial array in non-decreasing order $(a_1, a_2, …, a_n)$ using only allowed swaps. Otherwise, print “$NO$”.
Example
input
6
3 2
3 2 1
1 2
4 2
4 1 2 3
3 2
5 1
1 2 3 4 5
1
4 2
2 1 4 3
1 3
4 2
4 3 2 1
1 3
5 2
2 1 2 3 3
1 4
output
YES
NO
YES
YES
NO
YES
题解
我们先来考虑一种简单的情况,在 $p$ 的集合中有 $n - 2$ 个数,即:给定的数组 $a$ 当中,只有一个位置不能和它的后一个位置交换。
不妨设这个位置为 $i$ ,即 $a_1$ ~ $a_i$ 中的数字可以任意交换(因为总存在一种进行若干次相邻的交换的方式,使其达到任意交换的效果),同理,$a_{i + 1}$ ~ $a_n$ 中的数字也可以任意交换,此时,若不能够将整个序列交换成一个非降序序列的唯一条件就是:在原序列 $a_1$ ~ $a_i$ 中存在某个数,它在将整个序列排列成非降序之后的位置在 $i$ 之后,当然也可以反过来理解,就是在排序之后出现在第 $1$ ~ $i$ 位置上的数,在原序列 $a$ 中的位置在 $i$ 之后。
如果设 $ b$ 为排序之后的序列,则上述不满足题意的条件可以表示为:
$$
\exists{x}(x\in\lbrace{b_1, b_2, …, b_i}\rbrace \wedge x\in\lbrace{a_{i + 1}, a_{i + 1}, …, a_n}\rbrace \wedge x\notin\lbrace{a_1, a_2, …, a_i}\rbrace)
$$
当然,如果序列中存在两个数的数值相等,这两个数也应该独立处理,当做不同的数来看待。
可以发现,如果存在多个位置,这些位置都不能和其后一个位置进行交换的话,只需要多次判断是否满足上述条件,只要有一处满足,整个序列就不能按题意要求排列成非降序,直接输出 $NO$ 即可,反之,输出 $YES$.
这题的数据范围很小,就算每次枚举到一个上述位置,再从最左侧到该位置循环一遍判断,也不会 $TLE$, 该方法判断一组序列的时间复杂度是 $O(n^2)$ 的,再加上 $t$ 组测试数据,所以整体时间复杂度是 $O(t\cdot n^2)$.这里的 $t$ 和 $n$ 都是 $100$,所以也只有 $10^6$,所以暴力判断也可以顺利 $AC$.
当然,这里也有一个很明显的优化,对于上述的每一个不能交换的位置而言,我们关心的只有这个位置左侧的数中,出现在原序列 $a$ 的位置的最大值是多少。因为如果这个最大值都没有满足上述条件,则该位置左侧任何一个数都不可能满足条件,因此,只需要在循环每个位置是否能和下一个位置交换的同时,记录一下左侧的数在原序列中出现的位置的最大值即可。
优化后的做法在判断上述条件的时间复杂度只有 $O(n)$,由于之前需要排序,所以最终需要 $O(nlogn)$ 的时间来处理一组数据,所以这题在优化后时间复杂度可以达到 $O(t\cdot nlogn)$.
# include <iostream>
# include <cstring>
# include <algorithm>
using namespace std;
typedef pair<int, int> PII;
const int N = 110;
int n, m;
PII a[N];
bool p[N];
int main()
{
int T;
cin >> T;
while (T--) {
memset(p, false, sizeof p);
cin >> n >> m;
for (int i = 1; i <= n; i++) {
cin >> a[i].first;
a[i].second = i;
}
for (int i = 1; i <= m; i++) {
int pos;
cin >> pos;
p[pos] = true;
}
sort(a + 1, a + n + 1);
bool success = true;
int max_idx = 0;
for (int i = 1, j = 1; i < n; i++)
if (!p[i]) {
while (j <= i)
max_idx = max(max_idx, a[j++].second);
if (max_idx > i) {
success = false;
break;
}
}
cout << (success ? "YES" : "NO") << endl;
}
return 0;
}
C. Perform the Combo
You want to perform the combo on your opponent in one popular fighting game. The combo is the string $s$ consisting of $n$ lowercase Latin letters. To perform the combo, you have to press all buttons in the order they appear in $s$. I.e. if $s=$”abca” then you have to press ‘a’, then ‘b’, ‘c’ and ‘a’ again.
You know that you will spend $m$ wrong tries to perform the combo and during the $i$-th try you will make a mistake right after $p_i$-th button $(1 \leq p_i < n)$ $($i.e. you will press first $p_i$ buttons right and start performing the combo from the beginning$)$. It is guaranteed that during the $m+1$-th try you press all buttons right and finally perform the combo.
I.e. if $s=$”abca”, $m=2$ and $p=[1,3]$ then the sequence of pressed buttons will be ‘a’ (here you’re making a mistake and start performing the combo from the beginning), ‘a’, ‘b’, ‘c’, (here you’re making a mistake and start performing the combo from the beginning), ‘a’ (note that at this point you will not perform the combo because of the mistake), ‘b’, ‘c’, ‘a’.
Your task is to calculate for each button (letter) the number of times you’ll press it.
You have to answer $t$ independent test cases.
Input
The first line of the input contains one integer $t (1 \leq t \leq 10^4)$ — the number of test cases.
Then $t$ test cases follow.
The first line of each test case contains two integers $n$ and $m (2 \leq n \leq 2 \cdot 10^5, 1 \leq m \leq 2 \cdot 10^5)$ — the length of $s$ and the number of tries correspondingly.
The second line of each test case contains the string $s$ consisting of $n$ lowercase Latin letters.
The third line of each test case contains $m$ integers $p_1, p_2, …, p_m (1 \leq p_i < n)$ — the number of characters pressed right during the $i$-th try.
It is guaranteed that the sum of $n$ and the sum of $m$ both does not exceed $2 \cdot 10^5 (\sum{n} \leq 2 \cdot 10^5, \sum{m} \leq 2 \cdot 10^5)$
It is guaranteed that the answer for each letter does not exceed $2 \cdot 10^9$.
Output
For each test case, print the answer — $26$ integers: the number of times you press the button ‘a’, the number of times you press the button ‘b’, ……, the number of times you press the button ‘z’.
Example
input
3
4 2
abca
1 3
10 5
codeforces
2 8 3 2 9
26 10
qwertyuioplkjhgfdsazxcvbnm
20 10 1 2 3 5 10 5 9 4
output
4 2 2 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 9 4 5 3 0 0 0 0 0 0 0 0 9 0 0 3 1 0 0 0 0 0 0 0
2 1 1 2 9 2 2 2 5 2 2 2 1 1 5 4 11 8 2 7 5 1 10 1 5 2
Note
The first test case is described in the problem statement. Wrong tries are “a”, “abc” and the final try is “abca”. The number of times you press ‘a’ is $4$, ‘b’ is $2$ and ‘c’ is $2$.
In the second test case, there are five wrong tries: “co”, “codeforc”, “cod”, “co”, “codeforce” and the final try is “codeforces”. The number of times you press ‘c’ is $9$, ‘d’ is $4$, ‘e’ is $5$, ‘f’ is $3$, ‘o’ is $9$, ‘r’ is $3$ and ‘s’ is $1$.
题解
一个长度为 $n$ 的字符串,按顺序敲击键盘,一共出现了 $m$ 次失误,出现失误后从头开始敲,第 $m + 1$ 次完整将字符串中的字符都在键盘上以此敲击一遍。问 $26$ 个字母分别被敲了多少次。
数据范围很显然,暴力会 $TLE$,那么,我们来考虑如何优化。
对于每一次失误,我们需要计算的是在该次失误的位置 $p_i$ 以及之前的位置中各个字母出现的次数,求一段前缀的和,这也很明显可以用前缀和来进行优化。线性处理一遍前缀和数组之后,对于每一次失误,就只需要用 $O(26)$ 的时间复杂度将每个字母的按键次数累加进答案里。
综上,总的时间复杂度为 $O(26 \cdot n)$,能够完美解决此题。
# include <iostream>
# include <cstdio>
# include <cstring>
# include <algorithm>
using namespace std;
const int N = 2e5 + 5;
int n, m;
int sum[N][30], cnt[30];
char str[N];
int main()
{
int T;
scanf("%d", &T);
while (T--) {
scanf("%d %d", &n, &m);
for (int i = 1; i <= n; i++)
for (int j = 0; j < 26; j++)
sum[i][j] = 0;
scanf("%s", str + 1);
for (int i = 1; i <= n; i++) {
sum[i][str[i] - 'a']++;
for (int j = 0; j < 26; j++)
sum[i][j] += sum[i - 1][j];
}
for (int i = 0; i < 26; i++)
cnt[i] = sum[n][i];
while (m--) {
int pos;
cin >> pos;
for (int i = 0; i < 26; i++)
cnt[i] += sum[pos][i];
}
for (int i = 0; i < 26; i++)
printf("%d%c", cnt[i], " \n"[i + 1 == 26]);
}
return 0;
}
D. Three Integers
You are given three integers $a \leq b \leq c$.
In one move, you can add $+1$ or $−1$ to any of these integers (i.e. increase or decrease any number by one). You can perform such operation any (possibly, zero) number of times, you can even perform this operation several times with one number. Note that you cannot make non-positive numbers using such operations.
You have to perform the minimum number of such operations in order to obtain three integers $A \leq B \leq C$ such that $B$ is divisible by $A$ and $C$ is divisible by $B$.
You have to answer $t$ independent test cases.
Input
The first line of the input contains one integer $t (1 \leq t \leq 100)$ — the number of test cases.
The next $t$ lines describe test cases. Each test case is given on a separate line as three space-separated integers $a, b$ and $c (1 \leq a \leq b \leq c \leq 10^4)$.
Output
For each test case, print the answer. In the first line print $res$ — the minimum number of operations you have to perform to obtain three integers $A \leq B \leq C$ such that $B$ is divisible by $A$ and $C$ is divisible by $B$. On the second line print any suitable triple $A, B$ and $C$.
Example
input
8
1 2 3
123 321 456
5 10 15
15 18 21
100 100 101
1 22 29
3 19 38
6 30 46
output
1
1 1 3
102
114 228 456
4
4 8 16
6
18 18 18
1
100 100 100
7
1 22 22
2
1 19 38
8
6 24 48
题解
给你正整数 $a, b, c$,每次操作可以使一个数 $+1$ 或者 $-1$,假设操作后的数分别为 $A, B, C$,问最少需要操作多少次使得 $A \mid B$ 同时 $B \mid C$.
不难发现,如果满足上述条件的话,就一定有 $A \leq B \leq C $,否则整除关系就不可能成立。
同时也可以发现,如果 $A, B$ 确定了的话,那么 $C$ 的取值就只有两种情况:
- $\lfloor \frac{c}{B}\rfloor \cdot B$
- $\lceil \frac{c}{B}\rceil \cdot B = \lfloor \frac{c + B - 1}{B}\rfloor \cdot B$
也就是距离输入的整数 $c$ 最近的能够整除 $B$ 的两个数。此时就能用 $ |a - A| + |b - B| + |c - C| $ 来更新之前的答案。
聪明的小伙伴已经发现,这个做法对于每读入一组 $a, b, c$,都需要两重循环求解,而数据范围为 $1 \leq t \leq 100, 1 \leq a \leq b \leq c \leq 10^4$,那么会不会 $TLE$ 呐?下面就简单证明一下此方法并不会超时:
首先 $a$ 的取值一定在 $1$ ~ $10^4$ 之间,所以第一重循环需要枚举 $10^4$,也就是第一重循环确定了 $A$,此时由于需要满足 $A \mid B$ 这个条件,所以第二重循环只需要枚举 $A$ 的倍数,即:$A, 2A, 3A, …$,也就是第二重循环的枚举次数是跟 $A$ 相关的,假设第二重循环的数字的上限为 $n$,那么对于每一个确定的 $A$,都只需要枚举 $\frac{n}{A}$ 次,当 $A$ 增大,第二重循环的枚举次数会逐步降低。
综上,这两重循环的实际计算量为:
$$
\frac{n}{1} + \frac{n}{2} + \frac{n}{3} + … = n(1 + \frac{1}{2} + \frac{1}{3} + …)
$$
右侧括号内那一串为调和级数,它的极限为 $\ln (n + 1) + c$ ,这里的 $c$ 为欧拉常数,大概只有 $0.577$ 左右,所以对于每组 $a, b, c$,通过上述过程寻找答案的过程的时间复杂度为 $O(n \ln n)$,再加之 $t$ 组测试数据,所以时间复杂度为 $O(t \cdot n\ln n)$.能够完美在时限内出解。
剩下的问题就是第二重循环的上限是多少?
由于在计算 $C$ 的过程中有一个向上取整的操作,所以是有可能取到超过 $10000$ 的数的,所以一种简单的想法是不管三七二十一,直接将第二层循环设成 $20000$,而不去精确计算具体上限,因为写算法题的目的就是在时间限制内运行出结果,而此方法的时间复杂度完全可以胜任。(好吧,其实还有一点原因是盲猜取成 $10000$ 的两倍就能过,也不想花时间再算一个精确一点的上限,而且交上去直接就 $AC$ 了
# include <iostream>
# include <cmath>
# include <algorithm>
using namespace std;
int update(int c, int j, int& k)
{
int down = c - c / j * j, up = (c + j - 1) / j * j - c;
if (down <= up && down < c) {
k = c - down;
return down;
}
k = c + up;
return up;
}
int main()
{
int T;
cin >> T;
while (T--) {
int a, b, c;
cin >> a >> b >> c;
int A, B, C, res = 0x3f3f3f3f;
for (int i = 1; i <= 10000; i++)
for (int j = i; j <= 20000; j += i) {
int k, dis = abs(a - i) + abs(b - j) + update(c, j, k);
if (res > dis) {
res = dis;
A = i;
B = j;
C = k;
}
}
cout << res << endl << A << ' ' << B << ' ' << C << endl;
}
return 0;
}
E. Construct the Binary Tree
You are given two integers $n$ and $d$. You need to construct a rooted binary tree consisting of $n$ vertices with a root at the vertex $1$ and the sum of depths of all vertices equals to $d$.
A tree is a connected graph without cycles. A rooted tree has a special vertex called the root. A parent of a vertex $v$ is the last different from $v$ vertex on the path from the root to the vertex $v$. The depth of the vertex $v$ is the length of the path from the root to the vertex $v$. Children of vertex $v$ are all vertices for which $v$ is the parent. The binary tree is such a tree that no vertex has more than $2$ children.
You have to answer $t$ independent test cases.
Input
The first line of the input contains one integer $t (1 \leq t \leq 1000)$ — the number of test cases.
The only line of each test case contains two integers $n$ and $d (2 \leq n, d \leq 5000)$ — the number of vertices in the tree and the required sum of depths of all vertices.
It is guaranteed that the sum of $n$ and the sum of $d$ both does not exceed $5000 (\sum{n} \leq 5000, \sum{d} \leq 5000)$.
Output
For each test case, print the answer.
If it is impossible to construct such a tree, print “$NO$” (without quotes) in the first line. Otherwise, print “$YES$” in the first line. Then print $n−1$ integers $p_2, p_3, …, p_n$ in the second line, where $p_i$ is the parent of the vertex $i$. Note that the sequence of parents you print should describe some binary tree.
Example
input
3
5 7
10 19
10 18
output
YES
1 2 1 3
YES
1 2 3 3 9 9 2 1 6
NO
Note
Pictures corresponding to the first and the second test cases of the example:
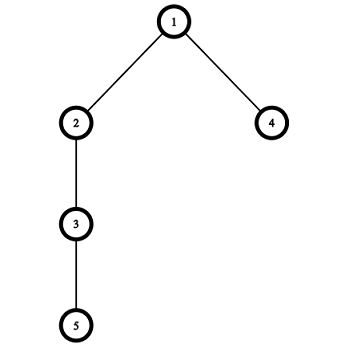
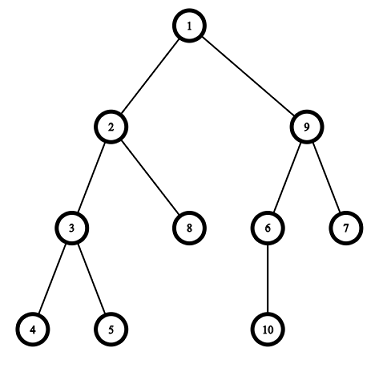
题解
一句话题意很简单,就是构造一棵 $n$ 个节点的二叉树,使其所有节点的深度之和(所有点到根节点的距离之和)恰好为 $d$.
可以先来考虑肯定无解的情况,即:要求的深度之和 $d$,小于 $n$ 个节点的二叉树所能构造成的最小深度和或者大于能够构造成的最大深度和。
那么最小深度之和怎么构造?也就是说每个节点都要尽可能靠近根节点,也就是将这 $n$ 个节点构造成一棵完全二叉树的样子;相反,最大深度之和,就是让每个节点都尽可能远离根节点,也就是构造成一条链的形式。
那么,如果在上述范围内,是否不论 $d$ 取何值都能构造出一棵二叉树满足条件?
我们先来看一种构造方式:
先将 $n$ 个节点构造成完全二叉树的形式,若此时的深度之和都比 $d$ 要大,说明无解;
否则,固定最左侧的这条链,取除了最左侧这条链之外的深度最深的点,将它放到最左侧链的末尾,然后如此循环,如果最终全都转移到了最左侧这条链上,则也无解。
当然,有解的情况是在向最左侧链上转移的时候产生的,那么如何判定呐?
我们来考虑有解的转折点,也就是,当取走右边的一个节点之后,设剩余 $n - 1$ 个节点的深度之和为 $deep$,此时若 $ d - deep <= maxdeep + 1$$(maxdeep$ 为剩余所有点最深的深度$)$,则可以将取走的这个结点,直接接到相应的深度上,此时,就构造出了一棵满足题意的二叉树。
现在就来证明一下上述构造方式一定能成功:
首先,如果 $d - deep = maxdeep + 1$,只需要将取下的这个结点直接接到最左侧这条链的末尾即可;
其次,由于当前的这个节点是第一次发生 $d - deep <= maxdeep + 1$ 这种情况,所以在比这个节点原位置的深度更深的深度,一定在最左侧这条链上可以分叉出一个右儿子来接取出的这个点。而如果 $d - deep$ 恰好等于该节点原位置的深度,则至少这个原位置可以容纳这个点使满足题意。
至此,就只剩下 $d - deep$ 小于该节点原位置深度的情况,配上一张插图来说明这种情况不可能发生:
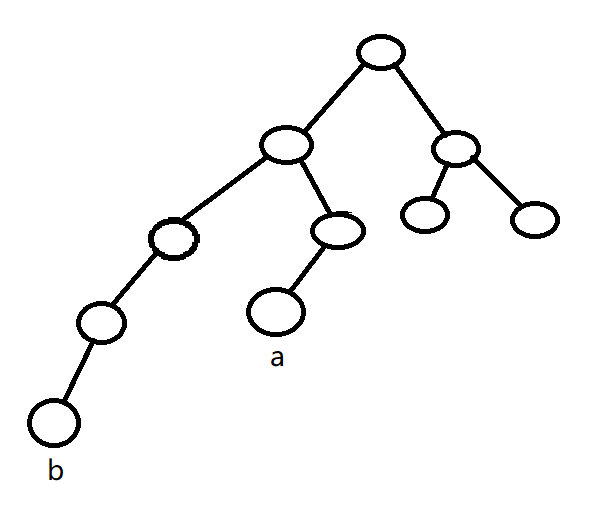
此时需要改变位置的为 $a$ 这个点,上一次更换到最左侧这条链的是 $b$ 这个点。
此时,先将 $a$ 移出去,依旧设剩余节点的深度之和为 $deep$,若 $d - deep < 3$, 如果能够证明 $b$ 这个点的位置一定放置错误,且正确放置后一定能构造出一棵满足条件的二叉树,则此问题就能够完美解决,接下来就来证明一下这一点。
易知,$a$ 处于原位置时,节点的深度之和为 $deep + 3$,此时将 $b$ 这个点也移回原位,如果严格按照上文描述的实现方式的话,$b$ 这个点的原位置应该为 $a$ 的兄弟节点,即:恢复原位之后的所有节点的深度之和为 $deep + 3 - 4 + 3 = deep + 2$.
至此,重新考虑将 $b$ 移动至新节点的操作,先删除 $b$, 则剩余点的深度之和为 $deep - 1$,此时结合 $d - deep < 3$, 可知 $d - deep + 1 \leq 3$,若 $d - deep + 1 = 3$,则可以转化为上文的一种情况,若该式依旧 $d - deep + 1 < 3$, 则可以继续重复恢复节点重新放置的操作。
我们也不难发现,在恢复节点时,从最左侧这条链准备恢复的节点的深度一定是大于该节点原位置的深度的,否则的话就与我们事先构造的是一棵完全二叉树矛盾;也就说明恢复重置节点的这个操作一定会结束,而且最终结束的条件只有满足下述两条之一:找到一个相应的位置使满足题意,或者直至重置成最初构造的完全二叉树。而一旦重置成最初的完全二叉树后若任不满足条件,则可知一定无解。
综上所述,该构造方法一定能够成立。
构造完全二叉树只需要进行一遍 $DFS$,同时记录下每个节点的深度,儿子结点有几个,父亲节点是谁以及最大深度等信息,可以方便后续对这棵二叉树的修改。
如果直接将某一个节点接到最左侧这条链的末尾,则只需要相应改动上述记录的信息即可;而如果找到了 $d - deep <= maxdeep + 1$ 的情况,也只要简单的 $DFS$ 将该节点插入到相应的深度即可,当然,加上该节点后,父节点的子节点个数不能超过 $2$ 个。
由于每组测试数据都只需要 $DFS$ 一次节点记录信息以及最后 $DFS$ 一次修改信息,中间枚举右侧每个节点是否转移的过程也是线性的,所以总体时间复杂度为 $O(t \cdot n)$.
# include <iostream>
# include <cstring>
# include <algorithm>
using namespace std;
const int N = 5010;
int n, d;
int max_depth, ver, deep;
int depth[N], son[N], ans[N];
bool vis[N], st[N];
void init()
{
for (int i = 1; i < N; i <<= 1)
vis[i] = true;
return;
}
void dfs(int u)
{
if (max_depth < depth[u]) {
max_depth = depth[u];
ver = u;
}
deep += depth[u];
if (u << 1 <= n) {
depth[u << 1] = depth[u] + 1;
ans[u << 1] = u;
son[u]++;
dfs(u << 1);
}
if ((u << 1 | 1) <= n) {
depth[u << 1 | 1] = depth[u] + 1;
ans[u << 1 | 1] = u;
son[u]++;
dfs(u << 1 | 1);
}
return;
}
bool insert(int u, int p, int deep)
{
if (depth[u] + 1 == deep) {
if (son[u] < 2) {
ans[p] = u;
return true;
}
return false;
}
if (u << 1 <= n && insert(u << 1, p, deep))
return true;
if ((u << 1 | 1) <= n && insert(u << 1 | 1, p, deep))
return true;
return false;
}
int main()
{
init();
int T;
cin >> T;
while (T--) {
max_depth = deep = 0;
memset(son, 0, sizeof son);
cin >> n >> d;
dfs(1);
if (d < deep) {
cout << "NO" << endl;
continue;
}
bool success = false;
for (int i = n; i; i--)
if (!vis[i]) {
int dp = depth[i];
deep -= dp;
int need = d - deep;
if (need > max_depth + 1) {
depth[i] = max_depth + 1;
son[ans[i]]--;
ans[i] = ver;
son[ver]++;
ver = i;
deep += depth[i];
max_depth++;
}
else {
depth[i] = need;
insert(1, i, need);
success = true;
break;
}
}
if (success) {
cout << "YES" << endl;
memset(st, false, sizeof st);
for (int i = 2; i <= n; i++)
cout << ans[i] << ' ';
cout << endl;
}
else
cout << "NO" << endl;
}
return 0;
}
F. Moving Points
There are $n$ points on a coordinate axis $OX$. The $i$-th point is located at the integer point $x_i$ and has a speed $v_i$. It is guaranteed that no two points occupy the same coordinate. All $n$ points move with the constant speed, the coordinate of the $i$-th point at the moment $t (t$ can be non-integer $)$ is calculated as $x_i + t \cdot v_i$.
Consider two points $i$ and $j$. Let $d(i,j)$ be the minimum possible distance between these two points over any possible moments of time (even non-integer). It means that if two points $i$ and $j$ coincide at some moment, the value $d(i,j)$ will be $0$.
Your task is to calculate the value $\sum_{1 \leq i < j \leq n} d(i, j) ($the sum of minimum distances over all pairs of points$)$.
Input
The first line of the input contains one integer $n (2 \leq n \leq 2 \cdot 10^5)$ — the number of points.
The second line of the input contains $n$ integers $x_1, x_2, …, x_n (1 \leq x_i \leq 10^8)$, where $x_i$ is the initial coordinate of the $i$-th point. It is guaranteed that all $x_i$ are distinct.
The third line of the input contains $n$ integers $v_1, v_2, …, v_n (-10^8 \leq v_i \leq 10^8)$, where $v_i$ is the speed of the $i$-th point.
Output
Print one integer — the value $\sum_{1 \leq i < j \leq n} d(i, j) ($the sum of minimum distances over all pairs of points$)$.
Example
input
3
1 3 2
-100 2 3
output
3
input
5
2 1 4 3 5
2 2 2 3 4
output
19
input
2
2 1
-3 0
output
0
题解
根据题意可以发现,如果两个点相向而行的话,那么总有一个时间点,这两个点会走到同一个位置,显然这两个点的 $dis = 0$.
如果两个点背道而驰,那么随着时间的不断推移,它们之间的距离只会不断增加,此时 $dis$ 应该为这两个点的初始位置的距离差。
如果两个点具有同方向的速度的话,则取决于初始位置落后的点是否能追上初始位置靠前的点,如果能追上,它们的 $dis = 0$,否则,随着时间流逝,它们之间的距离也只会越拉越大,此时,它们之间的 $dis$ 也应该为这两个点的初始位置的距离差。
根据以上分析可以得到,我们可以将此问题分为三个部分:
-
所有相向而行的点:此类点都会在某一个时刻相遇,所以对我们最终的答案没有任何贡献,所以实际上我们可以不用管这种情况。
-
所有背道而驰的点:它们中肯定一个点的速度向左,另一个的速度向右。所以我们可以实现根据速度的方向,将这 $n$ 个点分为两个部分,一部分的速度全部向左,记为 $L$,而另一部分的速度全部向右,记为 $R$。那么对于 $L$ 中的任意一个点,与之背道而驰的点就是在 $R$ 中初始位置位于该点右侧的点的数量,而它们之间的 $dis$ 之和可以简单计算为:$右侧所有满足该条件的点的距离之和 - 该点的初始位置 \cdot 右侧满足条件的点的数量。$现在的问题就转化为:对于 $L$ 中的每一个点,如何快速求出答案。
在 $R$ 中找出满足条件的点的数量,也就是找出 $R$ 中所有点根据初始位置排序后第一个满足条件的点,然后就能直接计算出所有满足条件的点的数量。那么在有序的数组中找出某一个位置,显然可以用二分来找。
那么,找到第一个满足条件的点之后,如何快速计算在该点之后的所有点的和呐?可以类似于前缀和,我们事先处理一个后缀和,这样,也能直接得到 $右侧所有满足该条件的距离之和$。
至此,对于 $L$ 中的每一个点,我们都可以通过上述方法,在 $log$ 的时间复杂度内求出答案。 -
两个点具有相同方向的速度:由于相同方向又可以分为负方向和正方向,而这两种情况的计算方式是类似的,我们这里只讨论两个点都具有负方向速度的情况:
假设现在有两个点 $a, b$,且 $a$ 在 $b$ 的左侧同时它们都具有负方向的速度,分别用 $a_v, b_v$ 表示。那么,如果 $b$ 要追上 $a$,那么当且仅当 $|b_v| > |a_v|$,即:$b_v < a_v$
上述思想启发我们,可以先将所有点$($该部分讨论的所有点均指具有负方向速度的点$)$根据初始位置排序,那么,其中某一个点 $p$,它对答案的贡献,就只需要考虑该点追不上的所有点与该点的距离差之和,即:在 $p$ 的左侧,所有速度小于等于 $p$ 的点与 $p$ 点的初始位置的距离差之和。那么现在的问题就转化为,对于每一个点,如何快速求出这个值。
我们先来考虑对于一个点 $p$,需要求出哪些值才能计算该点对答案的贡献。用类似第二部分的公式可以得出:$该点对答案的贡献 = 该点的初始距离 \cdot 左侧所有满足条件的点的数量 - 左侧所有满足条件的点的初始距离之和$
有了第二部分的讨论我们很自然可以想到前缀和是否能处理此问题,但是在计算完 $p$ 点对答案的贡献之后,需要将 $p$ 的信息也添加到后续的查询之中。也就是我们多了一步修改操作,这个操作前缀和是不支持的。
又要求前缀的和又要支持单点修改,那么也能很自然的想到用树状数组这一数据结构来维护,将每个点的速度作为下标,初始位置作为值,累加到树状数组中,每次修改和查询都是 $log$ 的时间复杂度,所以能够很完美解决此问题。
当然,由于速度的范围跨度比较大,所以先需要对所有点的速度进行离散化;而满足条件的点的数量,只需要再开一个树状数组同时维护即可。
同理,对于所有速度为正方向的点如何用树状数组维护,这里就不再啰嗦了,和上述思考方法类似,就留给读者自己推导了。
你以为这就完了嘛?当然没有,还有一种很特殊情况没有考虑,$v = 0$ (别问我为什么知道的,这个坑东西害我调了好久才 $AC$
先来考虑什么情况下这个点才会对答案产生贡献,不难发现,$对答案的贡献 = 该点左侧所有非正方向速度的点到该点的距离之和 + 该点右侧所有非负方向速的点度到该点的距离之和$
如果将该点加入到上文的 $L$ 中,那么在进行上文第二种情况的操作时,会将 $该点右侧所有正方向速度的点到该点的距离之和$ 累加进答案。
再来看上文第三种情况,如果当前枚举的点的速度为 $0$,那么,由于左侧所有点的速度都是非正的,所以就可以将 $该点左侧所有非正方向速度的点到该点的距离之和$ 累加到答案里。
聪明的小朋友可能会发现,不是还有一种情况没包含嘛,就是该点右侧所有速度为 $0$ 的点到该点的距离之和?
其实这种情况第三种操作中已经包含进去了,因为该点到右侧速度为 $0$ 的点的距离就等于右侧速度为 $0$ 的点往左边找,找到该点的距离。
至此,就能完美解决此题。
总结一下,就是:$排序 + 前缀和 + 二分 + 离散化 + 树状数组$ 即可顺利 $AC$,时间复杂度为 $O(nlogn)$.
# include <iostream>
# include <cstdio>
# include <cstring>
# include <vector>
# include <algorithm>
using namespace std;
typedef long long LL;
typedef pair<int, int> PII;
const int N = 2e5 + 5;
int n, X[N];
int l_cnt, r_cnt;
PII L[N], R[N];
vector<int> nums;
int cnt[N];
LL sum[N];
LL dis;
int get_pos(int p)
{
int l = 1, r = r_cnt;
while (l < r) {
int mid = l + r >> 1;
if (R[mid].first > p)
r = mid;
else
l = mid + 1;
}
if (R[l].first <= p)
l = -1;
return l;
}
void get_differ()
{
for (int i = r_cnt; i; i--)
sum[i] = sum[i + 1] + R[i].first;
for (int i = 1; i <= l_cnt; i++) {
int pos = get_pos(L[i].first);
if (pos == -1)
break;
dis += sum[pos] - 1ll * (r_cnt - pos + 1) * L[i].first;
}
return;
}
int get_idx(int x)
{
return lower_bound(nums.begin(), nums.end(), x) - nums.begin() + 1;
}
int lowbit(int x)
{
return x & -x;
}
void add(int pos, int c)
{
for (int i = pos; i <= nums.size(); i += lowbit(i)) {
sum[i] += c;
cnt[i]++;
}
return;
}
LL get_sum(int pos)
{
LL s = 0;
for (int i = pos; i; i -= lowbit(i))
s += sum[i];
return s;
}
int get_cnt(int pos)
{
int c = 0;
for (int i = pos; i; i -= lowbit(i))
c += cnt[i];
return c;
}
int main()
{
scanf("%d", &n);
for (int i = 1; i <= n; i++)
scanf("%d", X + i);
for (int i = 1; i <= n; i++) {
int v;
scanf("%d", &v);
if (v > 0)
R[++r_cnt] = { X[i], v };
else
L[++l_cnt] = { X[i], v };
nums.push_back(v);
}
sort(L + 1, L + l_cnt + 1);
sort(R + 1, R + r_cnt + 1);
get_differ();
sort(nums.begin(), nums.end());
nums.erase(unique(nums.begin(), nums.end()), nums.end());
memset(sum, 0, sizeof sum);
for (int i = 1; i <= l_cnt; i++) {
int pos = get_idx(L[i].second), c = get_cnt(pos);
dis += 1ll * c * L[i].first - get_sum(pos);
add(pos, L[i].first);
}
memset(sum, 0, sizeof sum);
memset(cnt, 0, sizeof cnt);
for (int i = r_cnt; i; i--) {
int pos = get_idx(R[i].second), c = get_cnt(nums.size()) - get_cnt(pos - 1);
dis += get_sum(nums.size()) - get_sum(pos - 1) - 1ll * c * R[i].first;
add(pos, R[i].first);
}
printf("%lld\n", dis);
return 0;
}
2020/02/27 Update:
在 @Patrick_Star 的启发下,$C$ 题可以从后往前加,记录一下当前位置及以后的位置一共出错的次数,那么 $该次数 + 1(最后一次完整敲击)$ 就是这个位置的字母的按键次数。
# include <iostream>
# include <cstring>
# include <algorithm>
using namespace std;
const int N = 2e5 + 5;
int n, m;
int wrong[N], res[30];
char str[N];
int main()
{
int T;
cin >> T;
while (T--) {
for (int i = 1; i < n; i++)
wrong[i] = 0;
memset(res, 0, sizeof res);
cin >> n >> m >> str + 1;
for (int i = 0; i < m; i++) {
int p;
cin >> p;
wrong[p]++;
}
int cnt = 1;
for (int i = n; i; i--) {
cnt += wrong[i];
res[str[i] - 'a'] += cnt;
}
for (int i = 0; i < 26; i++)
cout << res[i] << ' ';
cout << endl;
}
return 0;
}


逆乾太强了
C题其实可以用一个前缀和来处理的 然后从后往前加 一维数组就够了hh 不过老哥这个思路tql
对哦hh,从后往前扫一遍,记录一下这个位置以后的位置一共失误的次数,然后加上去就行了(๑•̀ㅂ•́)و✧
是的 乾坤大佬
tql
tql!
感谢捧场hh,第一次写这么长的题解
加油!