拓扑排序

如何输出字典序最小的拓扑排序？
将队列换成优先队列，优先队列取出的元素是当前字典序最小的编号，在出队的时候记录出队的编号即为当前字典序最小的拓扑序，此方法的时间复杂度是$O(logn∗(n+m))$
acwing1191

#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

const int N = 110, M = N * N / 2;

int n;
int h[N], e[M], ne[M], idx;
int q[N];
int d[N];

void add (int a, int b)
{
    e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}

void topsort()
{
    int hh = 0, tt = -1;
    for (int i = 1; i <= n; i ++ )
        if (!d[i])
            q[ ++ tt] = i;

    while (hh <= tt)
    {
        int t = q[hh ++ ];
        for (int i = h[t]; ~i; i = ne[i])
        {
            int j = e[i];
            if ( -- d[j] == 0)
                q[ ++ tt] = j;
        }
    }
}

int main()
{
    cin >> n;
    memset(h, -1, sizeof h);

    for (int i = 1; i <= n; i ++ )
    {
        int son;
        while (cin >> son, son)
        {
            add(i, son);
            d[son] ++ ;
        }
    }

    topsort();

    for (int i = 0; i < n; i ++ ) printf("%d ", q[i]);

    return 0;
}

拓扑排序+最长路

acwing1192
在差分约束问题中，以求最长路为例

• 边权无限制，则只能使用spfa
• 边权非负，使用tarjan缩点，缩点后每一个强连通分量内部只要有一个边权大于0，则无解（只要存在一条边权大于0的边，则该强连通分量内存在正环），换句话说，若问题有解，则任何一个SCC里所有边权都是0，
• 边权大于0，若有解则不能有环，即原图为DAG（拓扑图），对原图求一遍拓扑排序，再递推出每一个点距起点的最大值。
• 题目要求奖金总和最小，则每个人奖金最小时总和一定最小。反之，总和最小，每个点不一定最小。

#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

const int N = 10010, M = 20010;

int n, m;
int h[N], e[M], ne[M], idx;
int q[N];
int d[N];
int dist[N];

void add(int a, int b)
{
    e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}

bool topsort()
{
    int hh = 0, tt = -1;
    for (int i = 1; i <= n; i ++ )
        if (!d[i])
            q[ ++ tt] = i;

    while (hh <= tt)
    {
        int t = q[hh ++ ];
        for (int i = h[t]; ~i; i = ne[i])
        {
            int j = e[i];
            if ( -- d[j] == 0)
                q[ ++ tt] = j;
        }
    }

    return tt == n - 1;
}

int main()
{
    scanf("%d%d", &n, &m);
    memset(h, -1, sizeof h);
    while (m -- )
    {
        int a, b;
        scanf("%d%d", &a, &b);
        add(b, a);
        d[a] ++ ;
    }

    if (!topsort()) puts("Poor Xed");
    else
    {
        for (int i = 1; i <= n; i ++ ) dist[i] = 100;
        for (int i = 0; i < n; i ++ )
        {
            int j = q[i];
            for (int k = h[j]; ~k; k = ne[k])
                dist[e[k]] = max(dist[e[k]], dist[j] + 1);
        }

        int res = 0;
        for (int i = 1; i <= n; i ++ ) res += dist[i];

        printf("%d\n", res);
    }

    return 0;
}

acwing164
设从点 x 出发能够到达的点构成的集合是 f(x)，从点 x 出发能够到达的点，是从 x 的各个后继节点 y 出发能够到达的点的并集，再加上点 x 自身 。
先按照拓扑排序算法求出拓扑序，然后按照拓扑序的倒叙进行计算------因为在拓扑序中，任意一条边 (x , y)，x 都排在 y 之前。

std :: bitset 是标准库中的一个固定大小序列，其储存的数据只包含 0/1
众所周知，由于内存地址是按字节即 byte 寻址，而非比特 bit ,
我们一个 bool 类型的变量，虽然只能表示 0/1 , 但是也占了 1byte 的内存
bitset 就是通过固定的优化，使得一个字节的八个比特能分别储存 8 位的 0/1
对于一个 4 字节的 int 变量，在只存 0/1 的意义下， bitset 占用空间只是其
在某些情况下通过 bitset 可以使你的复杂度除以 32

#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
#include <bitset>
#include<vector>
using namespace std;

const int N = 30010, M = 30010;

int n, m;
int h[N], e[M], ne[M], idx;
int d[N], q[N];
bitset<N> f[N];
vector<int> G[N];

void add(int a, int b)
{
    e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}

void topsort()
{
    int hh = 0, tt = -1;
    for (int i = 1; i <= n; i ++ )
        if (!d[i])
            q[ ++ tt] = i;

    while (hh <= tt)
    {
        int t = q[hh ++ ];
        for (int i = h[t]; ~i; i = ne[i])
        {
            int j = e[i];
            if ( -- d[j] == 0)
                q[ ++ tt] = j;
        }
    }
}

int main()
{
    scanf("%d%d", &n, &m);
    memset(h, -1, sizeof h);
    for (int i = 0; i < m; i ++ )
    {
        int a, b;
        scanf("%d%d", &a, &b);
        add(a, b);
        d[b] ++ ;
    }

    topsort();
    for (int i = n - 1; i >= 0; i -- )
    {
        int j = q[i];
        f[j][j] = 1;
        for (int k = h[j]; ~k; k = ne[k])
            f[j] |= f[e[k]];
    }

    for (int i = 1; i <= n; i ++ ) printf("%d\n", f[i].count());

    return 0;
}

acwing456
停靠过的车站的等级一定严格大于为停靠过的车站的等级，因此车站的等级均有严格的大小关系，则不存在环，因此可以用拓扑排序每个车站在图中的大小关系，使用动态规划求出车站等级最大的最小值(和奖金一题类似，均为差分约束问题)
在建边的时候，最坏情况下是有1000趟火车，每趟有1000个点，每趟上限有500个点停站，则有(1000 - 500)个点不停站，不停站的点都向停站的点连有向边，则总共有500 * 500 * 1000 = 2.5 * 10^8,则会超内存，如果用邻接矩阵存储，需要遍历所有的边，遍历的次数也是2.5 * 10^8，因此会超时，所以在每趟火车所有不停站的点向所有停站的点连有向边时，中间添加一个ver辅助结点，如下图连接方式（转自小呆呆同学题解）

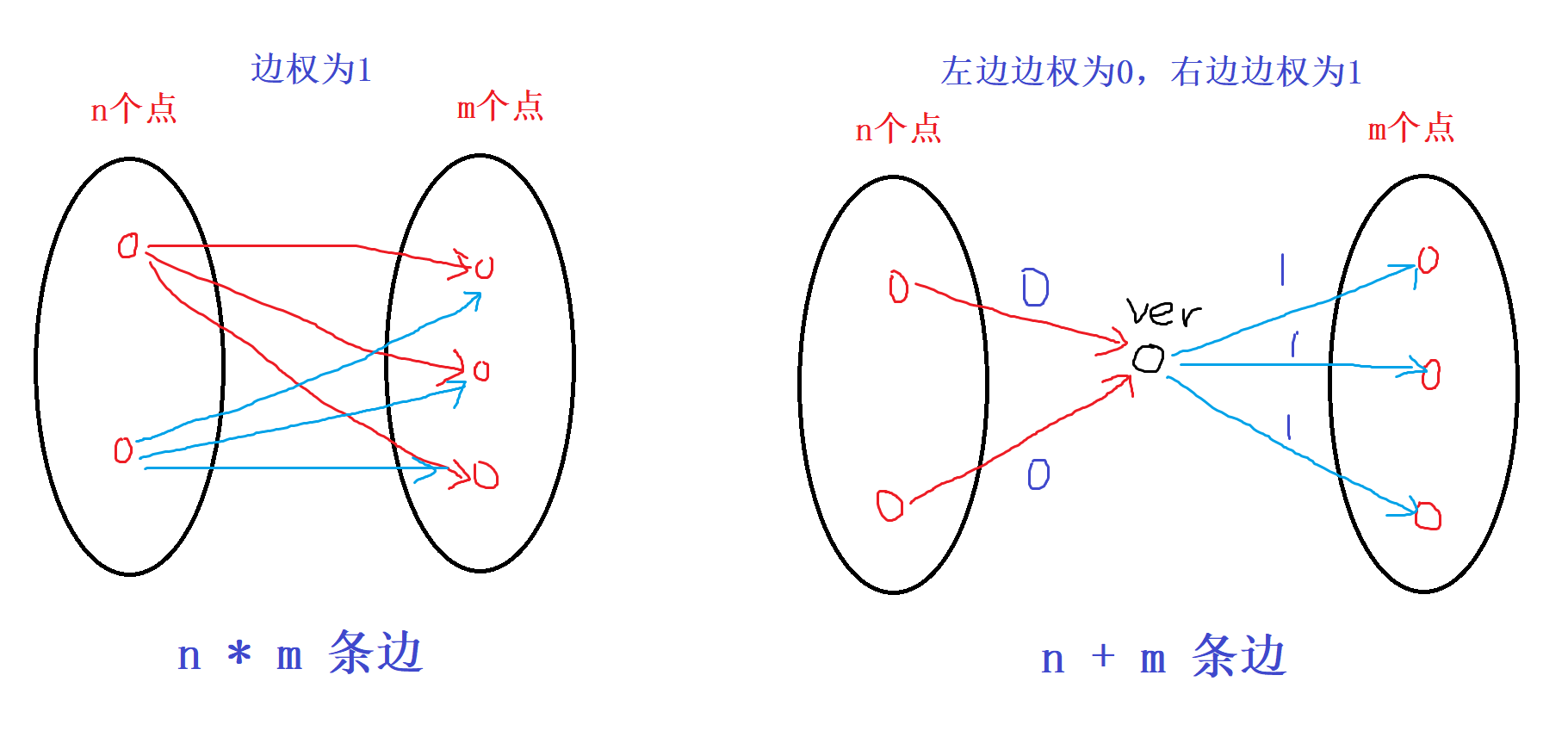
dist[i]：表示i点在拓扑图中离起点的最远距离(可能存在多起点)，dist[起点] == 1,边的权值为1

#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

const int N = 2010, M = 1000010;

int n, m;
int h[N], e[M], ne[M], w[M], idx;
int q[N], d[N];
int dist[N];
bool st[N];

void add(int a, int b, int c)
{
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++ ;
    d[b] ++ ;
}

void topsort()
{
    int hh = 0, tt = -1;
    for (int i = 1; i <= n + m; i ++ )
        if (!d[i])
            q[ ++ tt] = i;

    while (hh <= tt)
    {
        int t = q[hh ++ ];
        for (int i = h[t]; ~i; i = ne[i])
        {
            int j = e[i];
            if ( -- d[j] == 0)
                q[ ++ tt] = j;
        }
    }
}

int main()
{
    scanf("%d%d", &n, &m);
    memset(h, -1, sizeof h);
    for (int i = 1; i <= m; i ++ )
    {
        memset(st, 0, sizeof st);
        int cnt;
        scanf("%d", &cnt);
        int start , end;
        for(int i=1;i<=cnt;i++)
        {
            int stop;
            scanf("%d",&stop);
            if(i == 1)
                start = stop;
            if(i == cnt)
                end = stop;
            st[stop]=true;
        }

        int ver = n + i;
        for (int j = start; j <= end; j ++ )
            if (!st[j]) add(j, ver, 0);
            else add(ver, j, 1);
    }

    topsort();

    for (int i = 1; i <= n; i ++ ) dist[i] = 1;
    for (int i = 0; i < n + m; i ++ )
    {
        int j = q[i];
        for (int k = h[j]; ~k; k = ne[k])
            dist[e[k]] = max(dist[e[k]], dist[j] + w[k]);
    }

    int res = 0;
    for (int i = 1; i <= n; i ++ ) res = max(res, dist[i]);

    printf("%d\n", res);

    return 0;
}

acwing343

#include<iostream>
#include<cstring>
using namespace std;
const int N=30;
int g[N][N],d[N],temp[N];
int n,m,flag;//flag=1:有序 flag=-1:不确定
int q[N];

int TopoSort() //拓扑排序
{
    flag=1;
    int hh=0,tt=-1;
    for(int i=1;i<=n;i++)
    {
        temp[i]=d[i];//一边输入一边拓扑排序，所有入度数组不能改变    
    }  
    int m=0,cnt=0;
    for(int i=1;i<=n;i++)//查找入度为零的顶点个数，若>1，拓扑序不确定 
        if(temp[i]==0)
        {
            q[++tt]=i;
            cnt++;
        }
    if(cnt==0) return 0; //有环
    if(cnt>1) flag=-1; //不确定
    while(hh <= tt)
    {
        cnt=0;
        int t=q[hh++];
        for(int i=1;i<=n;i++)
            if(g[t][i])
            {
                temp[i]--;
                if(!temp[i])
                {
                    q[++tt]=i;
                    cnt++;
                }
            }
        if(cnt>1) flag=-1; //不确定        
    }
    if(tt < n-1)
        return 0;
    return flag;
}

int main()
{
    int sign;  //当sign=1时，已得出结果
    string str;
    while(cin>>n>>m)
    {
        if(m==0&&n==0) break;
        memset(g,0,sizeof g);
        memset(d,0,sizeof d);
        sign=0;
        for(int i=1;i<=m;i++)
        {
            cin>>str;
            if(sign) continue; //一旦得出结果，对后续的输入不做处理
            int x=str[0]-'A'+1;
            int y=str[2]-'A'+1;
            g[x][y]=1;
            d[y]++;
            int s=TopoSort();
            if(s==0) //有环
            {
                printf("Inconsistency found after %d relations.\n",i);
                sign=1;
            }
            if(s==1) //有序
            {
                printf("Sorted sequence determined after %d relations: ",i);
                for(int j=0;j<n;j++)
                    cout<<char(q[j]+'A'-1);
                printf(".\n");
                sign=1;
            }
        }
        if(!sign) //不确定
            printf("Sorted sequence cannot be determined.\n");
    }
    return 0;
}

poj3687
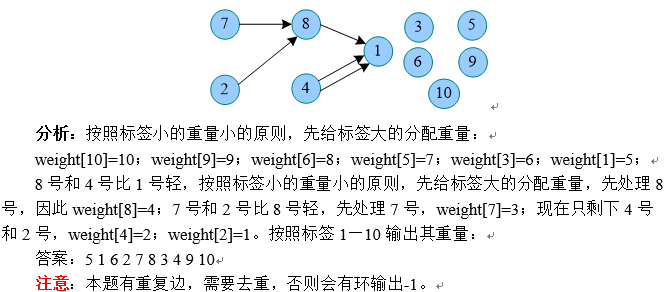
题意:给你N个球,编号从1到N.且这N个球的重量各不相同,且他们的重量正好是从1到N个单位.现在还给出了M个关系,每个关系描述了两个不同编号球之间的重量关系.现在要你输出这N个球可能的重量,从1号球到N号球.如果存在多解,则输出1号球最轻的解.如果1号球最轻时依然有多解,那么输出2号球最轻的解.依此类推.
分析:
其实这道题目我们可以理解成有1到N个孔,我们要把N个球放进去.如果2号球房间了5号孔,那么2号球重5个单位.现在我们要找出一个放球的方法,使得球序列满足M条约束且球序列的字典序最小.(球序列的字典序最小就保证了1号球最轻,2号球最轻等等)
以上分析是错误的.字典序最小的序列,并不能保证1号球最轻.
比如下面实例:

1
6 4
1 6
3 1
2 4
4 5

输出应为:23 1 4 5 6

拓扑排序字典序最小的序列是:2 3 1 4 5 6,转换成重量输出结果是3 1 2 4 5 6. 其中字典序最小的序列使得1号球的重量变成了3.
但是正确结果的拓扑排序应该是:3 1 2 4 5 6,转换成重量是:2 3 1 4 5 6.

这个序列使得1号球的重量变成了2,明显这个序列更优,但是字典序不一定最小.

其实上面的错误解法的思想是我们每次都优先选入度为0的最小序号的球放当前最小可用的格子.这样不能保证得到的解是1号球最轻的.比如23<1我们第一步肯定先放2,然后放3,再是1.但其实我们可以先放3,再1,再2的.这样1号球只重2个单位.

但是如果我们每次都是优先选出度为0的最大序号球放在当前可能的最大格子里,那么我们得到的解能保证1号球是最轻的.我们要放i号球的时候,一定要保证当前还没有被放的所有球中,只有明确比i号球轻的球或是序号<i的球.如果与i号球无关的球且序号大于i的话,那么明显我应该先放这个大序号的球到大编号格子上去.

#include<iostream>
#include<cstring>
#include<queue>
#include<cstdio>
using namespace std;
const int N=210;
int n,m;
int g[N][N];
int d[N];
int q[N];
int dist[N];
priority_queue<int> heap;
int cnt;
int w[N];

bool toposort()
{
    for(int i=1;i<=n;i++)
        if(!d[i])
            heap.push(i);

    while(heap.size())
    {
        int t=heap.top();
        heap.pop();
        q[cnt++]=t;
        //cout<<"--"<<t;
        for(int i=1;i<=n;i++)
            if(g[t][i] && --d[i] == 0)
                    heap.push(i);

     } 
     return cnt == n;
}

int main()
{
    int t;
    cin>>t;
    while(t--)
    {
        memset(g,0,sizeof g);
        memset(d,0,sizeof d);
        cnt=0;
        scanf("%d%d",&n,&m);
        while(m--)
        {
            int a,b;
            scanf("%d%d",&a,&b);
            if(!g[b][a])
            {
                g[b][a]=1;
                d[a]++;
            }
        }

        if(!toposort())
            cout<<-1<<endl;
        else 
        {
            int val=n;
            for(int i=0;i<n;i++)
            {
                w[q[i]]=val--;
            }

            for(int i=1;i<=n;i++)
                cout<<w[i]<<' ';
            cout<<endl;
        }
    }
}

poj1270

#include<iostream>
#include<string>
#include<cstring>
using namespace std;
const int maxn=50;
int g[maxn][maxn],d[maxn],s[maxn];//邻接矩阵，入度，标记出现 
int ans[maxn];
string str,ord;//字符串，秩序 
int len,num;//字符串长度，秩序长度 

void dfs(int t) //回溯法找所有的拓扑序 
{
    if(t == len)
    {
        for(int i=0;i<len;i++)
            cout<<char(ans[i]+'a');
        cout<<endl;
        return; 
    }
    for(int i=0;i<26;i++)
    {
        if(!d[i] && s[i])
        {
            s[i]--;
            for(int j=0;j<26;j++)
                if(g[i][j])
                    d[j]--;
            ans[t]=i;
            dfs(t+1);
            for(int j=0;j<26;j++)//回溯还原现场 
                if(g[i][j])
                    d[j]++;
            s[i]++;
        }   
    }
}

int main()
{
    while(getline(cin,str))
    {
        memset(g,0,sizeof g);
        memset(d,0,sizeof d);
        memset(s,0,sizeof s);
        len=str.length();
        int i,j=0;
        for(i=0;i<len;i++)
        {
            if(str[i]!=' ')
            {
                s[str[i]-'a']++;
                j++;
            }
        }
        len=j;
        getline(cin,ord);
        num=ord.length();
        for(i=0;i<num;i+=2)
        {
            int u=ord[i]-'a';
            i+=2;
            int v=ord[i]-'a';
            g[u][v]=1;
            d[v]++;
        }
        dfs(0);
        cout<<endl;
    }
    return 0;
}

P2883
题意很简单，求每一条边被几条从入度为0的点到n号点的路径覆盖过。

画一下图，再结合数学思想，可以发现对于一条边 x—>y，它的答案 = 从每个入度为0的点到x的路径数 * y到n号点的路径数。

那么怎么算入度为0的点到x的路径数呢？

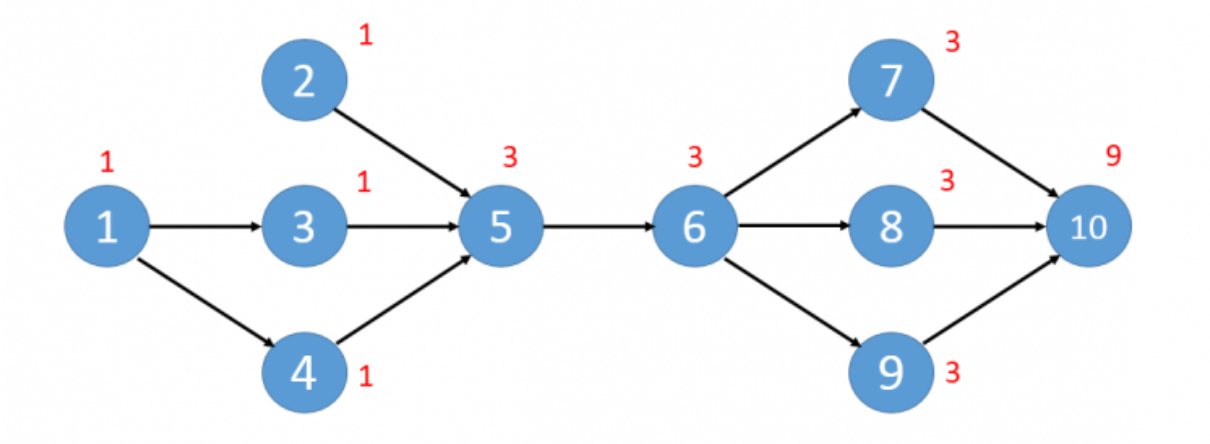
观察这张图，其中红色数字表示的是从入度为0的点到该点的路径数。

若设为v[i]，可以发现对于一个点i，它的答案是∑v[j]，其中j是i的前驱节点。

同理可以得到y到n号点的路径数的计算方法。

这样我们就可以建两张图，一张正图一张反图。

这样对于一条边x—>y (x<y)，它的答案就是v[正图][x] * v[反图][y]。统计并输出即可。

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<vector>
using namespace std;
const int N=5010;
vector<int> g[N],rg[N];
int din[N],dout[N];
int q[N];
int fin[N],fout[N];
vector<pair<int,int> > edge;
int n,m;

void toposort1()
{
    int hh=0,tt=-1;
    for(int i=1;i<=n;i++)
        if(!din[i])
        {
            fin[i]=1;
            q[++tt]=i;
        }

    while(hh<=tt)
    {
        int t=q[hh++];
        for(int i=0;i<g[t].size();i++)
        {
            int j=g[t][i];
            fin[j]+=fin[t];
            if(--din[j] == 0)
                q[++tt]=j;
        }
    }
}

void toposort2()
{
    int hh=0,tt=-1;
    for(int i=1;i<=n;i++)
        if(!dout[i])
        {
            fout[i]=1;
            q[++tt]=i;
        }

    while(hh<=tt)
    {
        int t=q[hh++];
        for(int i=0;i<rg[t].size();i++)
        {
            int j=rg[t][i];
            fout[j]+=fout[t];
            if(--dout[j] == 0)
                q[++tt]=j;
        }
    }
}

int main()
{
    cin>>n>>m;
    for(int i=0;i<m;i++)
    {
        int a,b;
        scanf("%d%d",&a,&b);
        g[a].push_back(b);
        rg[b].push_back(a);
        dout[a]++,din[b]++;
        edge.push_back({a,b});
    }

    toposort1();
    toposort2();

    int ans=0;
    for(int i=0;i<m;i++)
        ans=max(ans,fin[edge[i].first]*fout[edge[i].second]);

    cout<<ans<<endl;

    return 0;
}