并查集是一种处理集合关系的数据结构，顾名思义，并查集能合并、查询集合。
支持的操作如下：
查询某个元素在哪个集合中
合并两个集合
时间复杂度：均摊O(1) ，是一个非常优秀的数据结构

带权并查集

概念：在并查集的边上加上一些信息进行维护就是带权并查集
原理：并查集的边上存储与父亲结点有关的信息，一般需要满足可以向上合并，这样在路径
压缩时就可以合并信息到新的边上，至于合并操作，一般会给出要合并的两个结点之间的相
对关系，合并集合时根据以下关系实现

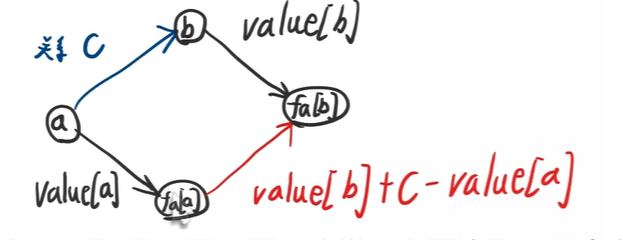
如图所示，给出关系c后，可以画出这样一个四边形，图中有2条路径可以从a到fa[b]而他们路径上的权值和（此处以求和为例）应该是相等的，这样就可以列出方程
value[a]+x=value[b]+c
移项后得到的就是合并时边权的取值x

如何统计连通块个数？

int res=0;
for(int i=1;i<=n;i++)
    if(p[i] == i)
        res++;

acwing1250
并查集解决的是连通性（无向图联通分量）和传递性（家谱关系）问题，并且可以动态的维护。抛开格子不看，任意一个图中，增加一条边形成环当且仅当这条边连接的两点已经联通，于是可以将点分为若干个集合，每个集合对应图中的一个连通块。
(二维坐标映射到一维)

#include<iostream>
using namespace std;
const int N=40010;
int p[N];
int n,m;

int get(int x,int y)
{
    return x*n+y;
}

int find(int x)
{
    if(x!=p[x])
        p[x]=find(p[x]);
    return p[x];
}

int main()
{
    cin>>n>>m;

    for(int i=0;i<n*n;i++)
        p[i]=i;

    int res=0;
    for(int i=1;i<=m;i++)
    {
        int x,y;
        char op;
        cin>>x>>y>>op;
        x--,y--;
        int d1=get(x,y);
        int d2;
        if(op=='D')
            d2=get(x+1,y);
        else 
            d2=get(x,y+1);
        int pa=find(d1);
        int pb=find(d2);
        if(pa==pb)
        {
            res=i;
            break;
        }
        else
            p[pa]=pb;
    }

    if(!res)
        cout<<"draw"<<endl;
    else    
        cout<<res<<endl;
    return 0;
}

acwing1252
并查集+01背包，把组团购买的物品看为一个商品

#include<iostream>
using namespace std;
const int N=10010;
int f[N];
int p[N];
int n,m,vol;
int v[N],w[N];

int find(int x)
{
    if(p[x]!=x) 
        p[x]=find(p[x]);    
    return p[x];
}

int main()
{
    cin>>n>>m>>vol;

    for(int i=1;i<=n;i++)
        cin>>v[i]>>w[i];

    for(int i=1;i<=n;i++)   
        p[i]=i;

    for(int i=1;i<=m;i++)   
    {
        int a,b;
        cin>>a>>b;
        int pa=find(a);
        int pb=find(b);
        if(pa != pb)
        {
            p[pa]=pb;
            v[pb]+=v[pa];
            w[pb]+=w[pa];
        }
    }

    for(int i=1;i<=n;i++)   
        if(p[i] == i)
            for(int j=vol;j>=v[i];j--)  
                f[j]=max(f[j],f[j-v[i]]+w[i]);

    cout<<f[vol]<<endl;
    return 0;
}

acwing237
先排序，把所有e==1的操作放在前面，然后再进行e==0的操作，在进行e==1的操作的时候，我们只要把它约束的两个变量放在同一个集合里面即可。在e==0，即存在一条不相等的约束条件，对于它约束的两个变量，如果在一个集合里面，那就不可能满足！如不相等的约束条件都满足，那就YES。
还有，我们要关注一下数据范围，是有10的9次方那么大，如果开一个10的9次方大的fa数组的话，空间肯定超限，所以，，我们需要用到离散化。

离散化是什么：一些数字，他们的范围很大（0-1e9），但是个数不算多（1-1e5），并且这些数本身的数字大小不重要，重要的是这些数字之间的相对大小（比如说某个数字是这些数字中的第几小，而与这个数字本身大小没有关系，要的是相对大小）（6 8 9 4 离散化后即为 2 3 4 1）（要理解相对大小的意思）（6在这4个数字中排第二小，那么就把6离散化成2，与数字6本身没有关系， 8,9,4亦是如此）

离散化分为保序的离散化（排序判重二分）和不要求保序的离散化(hash)。

#include<iostream>
#include<cstdio>
#include<unordered_map>
using namespace std;
const int N=2e6+10;
unordered_map<int,int> S;
int p[N];
int cnt;

struct Query
{
    int x,y,e;
}query[N];

int get(int x)
{
    if(S.count(x) == 0)
     {
         S[x]=++cnt;
     }
    return S[x];
}

int find(int x)
{
    if(p[x]!=x)
        p[x]=find(p[x]);
    return p[x];
}

int main()
{
    int t;
    scanf("%d",&t);
    while(t--)
    {
        int n;
        scanf("%d",&n);
        cnt=0;
        S.clear();

        for(int i=0;i<n;i++)
        {
            int x,y,e;
            scanf("%d%d%d",&x,&y,&e);
            query[i]={get(x),get(y),e};
        }

        for(int i=1;i<=cnt;i++)
        {
            p[i]=i;
        }

        bool flag=true;
        for(int i=0;i<n;i++)
            if(query[i].e == 1)
            {
                int pi=find(query[i].x);
                int pj=find(query[i].y);
                p[pi]=pj;
            }

        for(int i=0;i<n;i++)
            if(query[i].e == 0)
            {
                int pi=find(query[i].x);
                int pj=find(query[i].y);
                if(pi == pj)
                {
                    flag=false;
                    break;
                }
            }
        if(!flag)
            puts("NO");
        else
            puts("YES");
    }
    return 0;
}

poj1988

#include<cstdio>
#include<cstring>
using namespace std;
const int N=30010;
int n,p[N],d[N],cnt[N];

int find(int x)
{
    int fx=p[x];
    if(x!=p[x])
    {
        p[x]=find(p[x]);
        d[x]+=d[fx];
    }   
    return p[x];
}

int main()
{
    while(~scanf("%d",&n))
    {
        for(int i=1;i<N;i++)
        {
            p[i]=i;
            d[i]=0;
            cnt[i]=1;
        }
        while(n--)
        {
            char op[2];
            scanf("%s",op);
            if(op[0]=='C')
            {
                int x;
                scanf("%d",&x);
                int px=find(x);
                printf("%d\n",d[x]);
            }
            else
            {
                int x,y;
                scanf("%d%d",&x,&y);
                int px=find(x),py=find(y);
                p[px]=py;
                d[px]=cnt[py];
                cnt[py]+=cnt[px];
            }
        }
    }
    return 0;
}

类似题: acwing238

acwing240

边带权并查集

#include<cstdio>
#include<cstring>
using namespace std;
const int N=50010;
int n,m,p[N],d[N];
int res;

int find(int x)
{
    int fx=p[x];
    if(x!=p[x])
    {
        p[x]=find(p[x]);
        d[x]=(d[x]+d[fx])%3;
    }   
    return p[x];
}

int main()
{
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++)
    {
        p[i]=i;
        d[i]=0;
    }
    while(m--)
    {
        int c,x,y;
        scanf("%d%d%d",&c,&x,&y);
        if(x>n||y>n||(c==2&&x==y))
            res++;
        else
        {
            int px=find(x),py=find(y);
            if(c == 1)
            {
                if(px == py)
                {
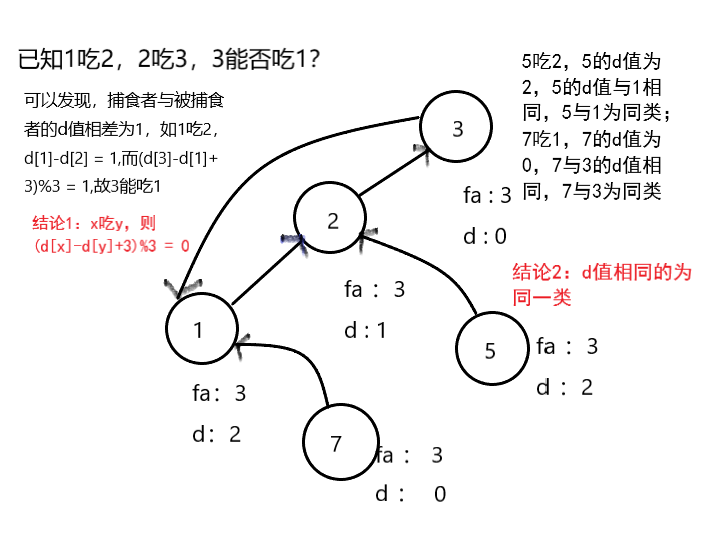
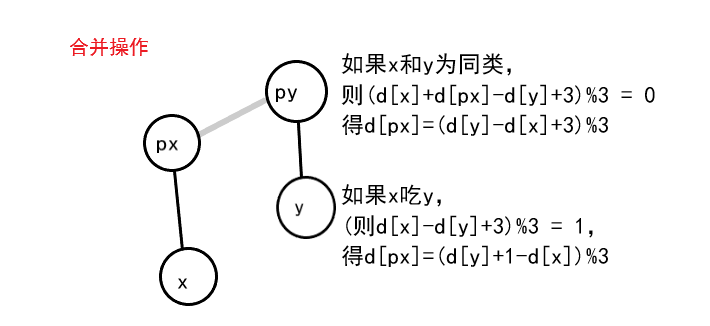
                    if((d[x] - d[y] + 3)%3)//x，y同类，则x，y的d值应该相同，该式值不为0说明有矛盾
                        res++;
                }
                else 
                {
                    p[px]=py;
                    d[px] = (d[y]-d[x]+3)%3;
                }
            }
            else 
            {
                if(px == py)
                {
                    if((d[x] - d[y] +3)%3 != 1)//x吃y，x，y的d值差为1，若不为1说明有矛盾
                        res++;
                }
                else 
                {
                    p[px]=py;
                    d[px] =  (d[y]+1-d[x])%3;
                }
            }
        }
    }
    printf("%d\n",res);
    return 0;
}

扩展域并查集

拓展域并查集解决了一种多个有相互关系的并查集，放在一起考虑的问题。一般的并查集应用一般就是判断在不在一个集合，拓展域并查集讲的是多个集合之间有相互关系，一般为相互排斥关系，判断是否在一个集合等。

首先对与最简单的并查集来说，如果两个是同一类，那么就 p[pa]=pb对吧，但是对于两个相互排斥类的怎么办呢，这就涉及到拓展与并查集了，首先想法就是建立两个并查集，但是怎么把两个并查集联系起来呢------拓展个体。

这里的拓展个体是什么意思呢，一个个体我们要拆成多个，比方说两个集合存在队立关系，那么对于一个个体a，我们假设存在一个个体 a+n ，a和a+n这两个是处于对立关系的，所以当我们说 a 和 b对立的时候，意思就是在说，a + n 和 b在同一并查集，b+n和a在同一并查集，当我们说，a和b是同类的时候，那么也就是说 a和b属于一个并查集，且a+n和b+n属于一个并查集。

这样就建出了多个并查集，解决了多个集合的相互关系。

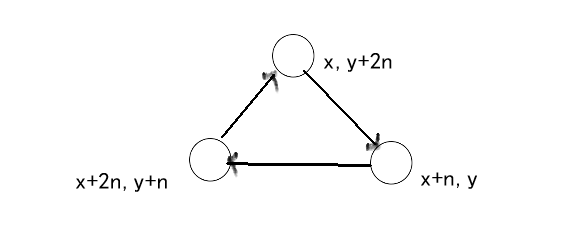
这道算是最经典的拓展域并查集题目了，A吃B，B吃C，C吃A，那么我们就需要三个并查集，也就是原数组扩展3倍。

A和B是同类说明了：

• A和B在同一并查集 。
• A+n和B+n在同一并查集 。
• A+2n和B+2n在同一并查集。

A吃B说明了：

• A+n和B是同类。
• A+2*n和B+n是同类。
• A和B+2*n是同类。

我们将一个动物拆成3个来存储，一个代表自身，第二个代表它的猎物，第三个代表它
的天敌。
例如：x和y是同类，那么x的猎物和y的猎物也应该是同类，x的天敌和y的天敌也应该是同类，那么这些同类应该在并查集中是连通的。
再例如：x吃y，那么x的猎物和y是同类，y的猎物和x的天敌应该是同类，这些同类都应该连通在同一个连通块中。
对于每一个输入，通过已有的连通信息判断是否错误，如果不是错误的，那么就可以作为新的信息来使用了。

#include<iostream>
#include<stdio.h>
using namespace std;
const int N=150010;
int p[N];//对于每种生物：设 x 为本身，x+n 为猎物，x+2*n 为天敌

int find(int x)
{
    if(x != p[x])
        p[x]=find(p[x]);
    return p[x];
}

void merge(int x,int y)
{
    if(find(x)!=find(y))p[find(x)]=find(y);
}

int main()
{
    int n,k;
    scanf("%d%d",&n,&k);
    int ans=0;
    int d,x,y;
    for(int i=1;i<=3*n;i++)
    {
        p[i]=i;
    }
    while(k--)
    {
        scanf("%d%d%d",&d,&x,&y);
        if(x>n||y>n)
        {
            ans++;continue;
        }
        if(d==1)
        {
            if( find(x+n) == find(y) || find(y+n) == find(x)) ans++;//x吃y或y吃x均与x与y是同类相矛盾
            else merge(x,y),merge(x+n,y+n),merge(x+2*n,y+2*n);
        }
        else
        {
            if( find(x) == find(y) || find(y+n) == find(x)) ans++;//x和y同类或y吃x与x吃y相矛盾
            else merge(x+n,y),merge(x,y+2*n),merge(y+n,x+2*n);
        }
    }
   printf("%d\n",ans);
}

acwing239
转自xxh同学题解

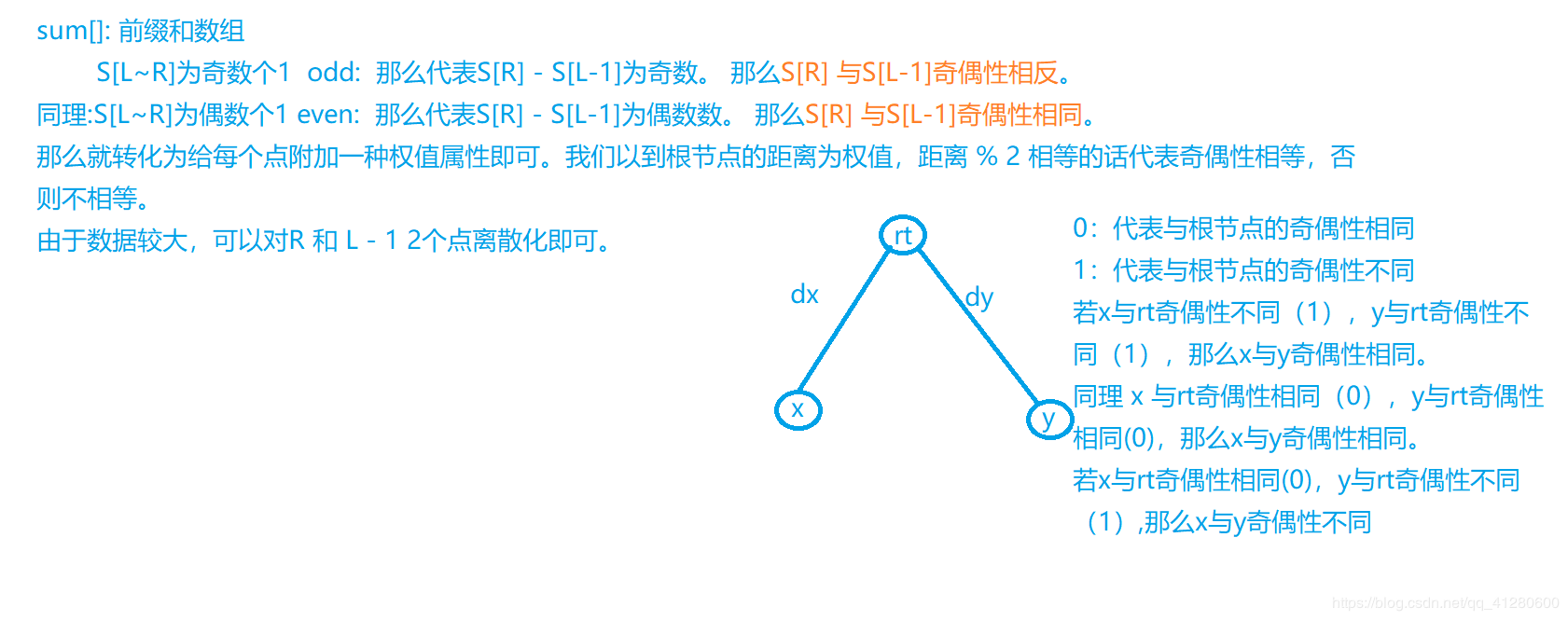
边带权并查集

边权d[x] = 0便是x与fa[x]奇偶性相同，为1表示x与fa[x]奇偶性不同。（模2意义下的加法相当于异或运算）

#include <cstring>
#include <iostream>
#include <algorithm>
#include <unordered_map>

using namespace std;

const int N = 20010;

int n, m;
int p[N], d[N];
unordered_map<int, int> S;

int get(int x)
{
    if (S.count(x) == 0) S[x] = ++ n;
    return S[x];
}

int find(int x)
{
    int px=p[x];
    if (p[x] != x)
    {
        p[x] = find(p[x]);
        d[x] ^= d[px];
    }
    return p[x];
}

int main()
{
    cin >> n >> m;
    n = 0;

    for (int i = 0; i < N; i ++ ) p[i] = i;

    int res = m;
    for (int i = 1; i <= m; i ++ )
    {
        int a, b;
        string type;
        cin >> a >> b >> type;
        a = get(a - 1), b = get(b);//前缀和思想

        int t = 0;
        if (type == "odd") t = 1;

        int pa = find(a), pb = find(b);
        if (pa == pb)
        {
            if (((d[a] ^ d[b]) != t))
            {
                res = i - 1;
                break;
            }
        }
        else
        {
            p[pa] = pb;
            d[pa] = d[a] ^ d[b] ^ t;
        }
    }

    cout << res << endl;

    return 0;
}

扩展域写法

#include <cstring>
#include <iostream>
#include <algorithm>
#include <unordered_map>

using namespace std;

const int N = 40010, Base = N / 2;

int n, m;
int p[N];
unordered_map<int, int> S;

int get(int x)
{
    if (S.count(x) == 0) S[x] = ++ n;
    return S[x];
}

int find(int x)
{
    if (p[x] != x) p[x] = find(p[x]);
    return p[x];
}

int main()
{
    cin >> n >> m;
    n = 0;

    for (int i = 0; i < N; i ++ ) p[i] = i;

    int res = m;
    for (int i = 1; i <= m; i ++ )
    {
        int a, b;
        string type;
        cin >> a >> b >> type;
        a = get(a - 1), b = get(b);

        if (type == "even")
        {
            if (find(a + Base) == find(b))//a，b奇偶性不同
            {
                res = i - 1;
                break;
            }
            p[find(a)] = find(b);
            p[find(a + Base)] = find(b + Base);
        }
        else
        {
            if (find(a) == find(b))//a，b奇偶性相同
            {
                res = i - 1;
                break;
            }

            p[find(a + Base)] = find(b);
            p[find(a)] = find(b + Base);
        }
    }

    cout << res << endl;

    return 0;
}

hdu3038
题目大意：
有一个数列长度为n，然后给出m个描述，每个给出一个区间上的和，要求这m个描述中有多少个是会和前面的描述冲突的
题解：
对于这个题目，我们是不知道数列的具体内容的，只知道若干区间上的和是多少，然而如果区间是相邻的，那么他们可以组合成一个更大的区间，也就是通过已有区间能推理出更多的区间和。
这道题使用带权并查集的做法很好处理，每一个结点表示一个区间的起点，
它的父亲结点表示这个左闭右开区间的右端点，边上的权值就存这个左闭右开区间上的和。
对于给出的每一个描述，都判断是否连通，如果是，就判断给出的数据和推得的数据是否吻合，如果不连通，就通过并查集的合并操作使其连通。

很明显，这题主要维护序列上每个节点之间的连通关系，以及节点之间的偏移量。我们定义 d[x]=x→root=sum[root]−sum[x]d[x]=x→root=sum[root]−sum[x]，即区间 [x+1,root] 的和。这里有一个需要注意的地方，我们不能令 d[x]=x→root=[x,root]区间和，因为 d[x] 初始化时为 0，而如果是 [x,root]的区间和，那么初始化时 d[x]=a[x]=[x,x] 区间和，而不是0，因此会发生错误。所以我们维护的是 d[x]=x→root=sum[root]−sum[x]

code

poj1703

并查集维护不同集合间的关系

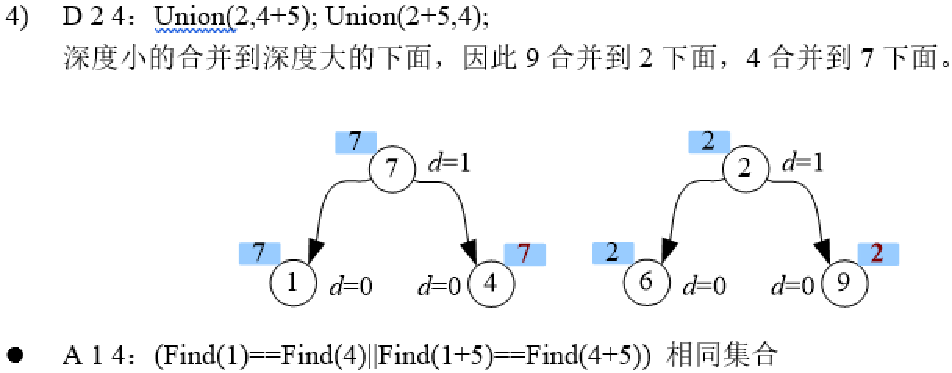
#include<cstdio>
#include<cstring>
#define MAXN 100010
using namespace std;
int n,m;
int fa[MAXN*2],d[MAXN*2]; //d用来区分树的高度，但其不存储树的具体高度

void Init()
{
    for(int i=1;i<=2*n;i++)
    {
        fa[i]=i;
        d[i]=0;
    }   
}

int Find(int x)
{
    if(x!=fa[x])
        fa[x]=Find(fa[x]);  
    return fa[x];
}

void Union(int x,int y)
{
    int a=Find(x);
    int b=Find(y);
    if(a==b) return;
    if(d[a]>d[b]) //启发式合并，就是把矮的树合并到高的树之下
        fa[b]=a;
    else
    {
        fa[a]=b;
        if(fa[a]==fa[b])//若树的高度一样，合并后作为父亲的树d+1
            d[b]++;
    }
}

int main()
{
    int T;
    scanf("%d", &T);
    while(T--)
    {
        scanf("%d%d",&n,&m);
        Init();
        while(m--)
        {
            char ch[2];
            int x,y;
            scanf("%s%d%d",ch,&x,&y);
            if(ch[0]=='D')
            {
                Union(x,y+n);
                Union(x+n,y);
            }
            else{
                if(Find(x+n)==Find(y))
                    printf("In different gangs.\n");
                else if(Find(x)==Find(y))
                        printf("In the same gang.\n");
                    else
                        printf("Not sure yet.\n");
            }
        }
    }
    return 0;
}

acwing257
首先开结构体存储每一条关系，并将结构体按照仇恨值由大到小排序。对循环读入的每一组关系来说，如果一个人还没有仇人，就把他的仇人设为那个人；如果这个人有仇人了，因为排序是从大到小的，所以我们将他们的仇人关在一起。对于另一个人也是试用的。如果读入的某组数据里两个人在同一个并查集内，这个时候直接输出当前的仇恨值就好了（从大到小排的序嘛）。由于记录敌人可能比较麻烦，那我们不妨将并查集开到2*n，定义某个人+n就是他的敌人，这样可以直接进行自己与敌人的敌人的合并操作。

我们要使怒气值大的一对人尽量不在同一间监狱里，先排个序。
建立两个集合，按照“敌人的敌人是朋友”这样的关系分组
接下来每次操作取出一个关系，看矛盾的两个人x和y是否已经分配到同一个集合中，那么还分如下两种情况：

• 如果在一起那么一定会矛盾那么直接输出当前的矛盾之即可，排序保证当前一定最小。
• 如果不在同一组，则按照“敌人的敌人就是朋友”的原则，把x与y的其他敌人分在同一组，y与x的其他敌人分在同一组
  不断进行以上操作最终可以得到答案

#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cstdlib>
#include<cstring>
using namespace std;
const int maxn=50010;
const int maxm=100010;
int n,m;
int fa[maxn];
struct crime
{
    int x,y,c;
}a[maxm];
int find(int x)
{
    if(fa[x]!=x) fa[x]=find(fa[x]);
    return fa[x];
}

void merge(int x,int y)
{
    if(find(x)!=find(y))
    {
        fa[find(x)]=find(y);
    }
}

bool check(int x,int y)
{
    if(find(x)==find(y)) return true;
    else return false;
}

bool cmp(const crime &a,const crime &b)
{
    return a.c>b.c;
}
int main()
{
    cin>>n>>m;
    for(int i=1;i<=m;i++)
    {
        cin>>a[i].x>>a[i].y>>a[i].c;
    }
    for(int i=1;i<=2*n;i++)
    {
        fa[i]=i;
    }
    sort(a+1,a+m+1,cmp);
    for(int i=1;i<=m;i++)
    {
        if(check(a[i].x,a[i].y))
        {
            cout<<a[i].c<<endl;
            return 0;
        }
        merge(a[i].x,a[i].y+n);//俗话说得好，敌人之敌亦吾之友，这道题就利用这个思路来解决。
        merge(a[i].y,a[i].x+n);
    }
    cout<<"0"<<endl;
    return 0;
}

POJ2492
Hopper教授正在研究一种罕见的虫子，这种虫子有两种性别。他猜想，这种虫子的交配行为总会由两只性别不同的虫子来完成。
为了验证他的假说，Hopper教授养了 𝑛 只虫子，共观察到 𝑚 次发生在它们之间的交配行为。他想知道，他的假说是否会被推翻，即是否一定发生了同性虫子间的交配行为。

例如，下面的数据即可推翻教授的假设（n=3,m=3）：
1 2
2 3
3 1

原本的并查集只能处理朋友关系，而在这道题里需要处理的是对立关系。于是，本题利用的中心思想是敌人的敌人就是朋友（异性的异性就是同性）。
虚构元素𝑥 + 𝑛表示𝑥的相反性别，将元素总数扩大二倍。得到𝑥与𝑦之间的一对关系的时候，就将𝑥与𝑦 + 𝑛，𝑦与𝑥 + 𝑛所处集合合并。

别解：二分图染色

还可以和普通的并查集一样，用一个集合来维护建立了相互关系的虫子。一个集合中的虫子分为两种性别。我们不妨给并查集中每一个元素𝑖记录权值di，表示𝑖与其在并查集中的父亲的关系。di = 0表示𝑖和父亲性别相同，di = 1表示性别不同。
路径压缩时，需要注意di也要更新为𝑖与根节点的关系。
code

P2661
有 n (n≤200000)个同学（编号为 1 到 n ）正在玩一个信息传递的游戏。在游戏里每人都有一个固定的信息传递对象，其中，编号为 i 的同学的信息传递对象是编号为 Ti 的同学。
游戏开始时，每人都只知道自己的生日。之后每一轮中，所有人会同时将自己当前所知的生日信息告诉各自的信息传递对象（注意：可能有人可以从若干人那里获取信息， 但是每人只会把信息告诉一个人，即自己的信息传递对象）。当有人从别人口中得知自 己的生日时，

输入格式
共2行。
第1行包含1个正整数 n ，表示 n 个人。
第2行包含 n 个用空格隔开的正整数 T1,T2,⋯⋯ ,Tn，其中第 i个整数 Ti 表示编号为 i 的同学的信
息传递对象是编号为 Ti 的同学， Ti≤n且 Ti≠i 。

输出格式
1个整数，表示游戏一共可以进行多少轮。
游戏结束。请问该游戏一共可以进行几轮

输入样例
5
2 4 2 3 1
输出样例
3

题目大意：找出有向图的最小环
题解：使用并查集判断是否构成环，如果构成就求出它的大小，环的长度为到父亲结点上的点数（边数+1）
code

poj2236
题意：
　　有一个计算机网络的所有线路都坏了，网络中有n台计算机，现在你可以做两种操作，修理（O）和检测两台计算机是否连通（S），只有修理好的计算机才能连通。连通有个规则，两台计算机的距离不能超过给定的最大距离D（一开始会给你n台计算机的坐标）。检测的时候输出两台计算机是否能连通。

思路：
　　每次修理好一台计算机的时候就遍历一下所有修好的计算机，看距离是否<=D，如果符合说明可以连通，将两台计算机所在集合合并。
　　每次检查的时候判断一下这两台计算机是否在同一集合中即可。

#include<iostream>
#include<cstdio>
using namespace std;
const int N=1010;
int p[N],x[N],y[N];
bool g[N][N];
int city[N],cnt;
int n,m;

inline bool check(int a,int b,int c,int d)
{
    return (a-c)*(a-c)+(b-d)*(b-d) <= m*m;
}

inline int find(int x)
{
    if(x != p[x])
        p[x]=find(p[x]);
    return p[x];
}

int main()
{
    cin>>n>>m;

    for(int i=1;i<=n;i++)
    {
        scanf("%d%d",x+i,y+i);
        p[i]=i;
    }

    for(int i=1;i<=n;i++)   
        for(int j=i+1;j<=n;j++)
            if(check(x[i],y[i],x[j],y[j]))
                g[i][j]=g[j][i]=1;

    char op[2];
    while(~scanf("%s",op))
    {
        if(*op == 'O') 
        {
            int x;
            scanf("%d",&x);
            city[cnt++]=x;

            for(int i=0;i<cnt-1;i++)
                if(g[city[i]][x])
                {
                    int pa=find(x);
                    int pb=find(city[i]);
                    if(pa != pb)
                        p[pa]=pb;
                }
        }
        else 
        {
            int a,b;
            scanf("%d%d",&a,&b);
            int pa=find(a);
            int pb=find(b);
            if(pa == pb)
                puts("SUCCESS");
            else 
                puts("FAIL");
        }
    }

    return 0;

}

两点之间的距离预处理g[i][j]表示是否能够通信。

hdu3635
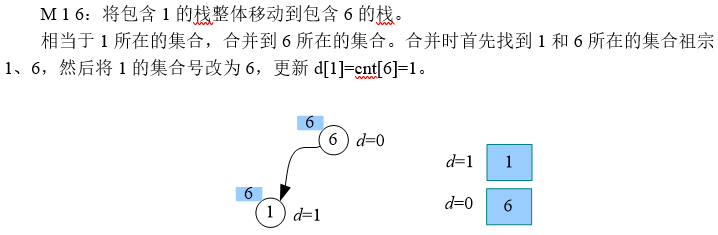
题意：有n个龙珠，n个城市。初始状态第i个龙珠在第i个城市里。接下来有两个操作：

T A B：把A号龙珠所在的城市的所有龙珠全部转移到B城市中。

Q A：查询A龙珠，要求：A龙珠所在城市，该城市龙珠数量，A移动的次数。

思路：用并查集可以轻松解决Q的前两个问题。关键在于如何统计A的移动次数，因为在T的时候是要将A所在城市的所有龙珠都要转移到B，那就要A集合里所有龙珠的移动次数都+1。假如我们在每一次转移前都去遍历一遍集合，显然是会TLE的，于是想了一个懒惰更新的方法。就是每次移动的时候只更新当前根节点的移动次数+1，合并的时候并在另一个树的根节点上。下一次移动这一个整棵树的时候必然要路径压缩，在路径压缩的时候将之前未更新的值更新即可。

#include<iostream>
#include<cstdio>
using namespace std;
const int N=10010;
int p[N];
int num[N];
int step[N];
int n,m;

inline int find(int x)
{
    int px=p[x];
    if(x != p[x])
    {
        p[x]=find(p[x]);
        step[x]+=step[px];
    }
    return p[x];
}

int main()
{
    int T;
    cin>>T;
    int kas=1;
    while(T--)
    {
        printf("Case %d:\n",kas++);
        scanf("%d%d",&n,&m);

        for(int i=1;i<=n;i++) p[i]=i,num[i]=1,step[i]=0;

        while(m--)
        {
            char op[2];
            scanf("%s",op);
            if(*op == 'T')
            {
                int a,b;
                scanf("%d%d",&a,&b);
                int pa=find(a);
                int pb=find(b);
                if(pa != pb)
                {
                    p[pa]=pb;
                    num[pb]+=num[pa];
                    step[pa]++; 
                }   
            }
            else 
            {
                int x;
                scanf("%d",&x);
                int px=find(x);
                printf("%d %d %d\n",px,num[px],step[x]);
            }
        }   
    }
}

hdu6109
本题中仅有相等关系满足传递性，不等关系是不满足传递性的，所以不能完全用并查集维护。

考虑这样：用set记录每个集合一定不相等的元素集合的集合，每次合并相同节点的时候将两个结点的set合并放到根节点处。每次对输入的相等关系，判断两个变量的根节点所维护的set是否含有对方的根节点，若没有则允许合并；对输入的不等关系，只需要判断两个元素是否在同一个集合中，若不在则将各自的根节点加入对方根节点的set中。

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<set>
using namespace std;
const int N=1e5+10;
int p[N];
set<int> s[N];
int ans[N],cnt;
int n;

void init()
{
    for(int i=0;i<=n;i++) p[i]=i,s[i].clear();
}

int find(int x)
{
    if(x != p[x])
        p[x]=find(p[x]);
    return p[x];
}

void merge(int a,int b)
{
    int pa=find(a),pb=find(b);
    if(pa == pb) return;
    p[pa]=pb;
    set<int>::iterator it;
    for(it = s[pa].begin();it != s[pa].end();it++)
        s[pb].insert(*it);
}

int main()
{
    scanf("%d",&n);
    init();

    int tim=0;
    for(int i=0;i<n;i++)
    {
        tim++;
        int u,v,e;
        scanf("%d%d%d",&u,&v,&e);
        int pu=find(u);
        int pv=find(v);
        if(e == 1)
        {
            if(pu == pv) continue;
            if(s[pu].find(pv) == s[pu].end() && s[pv].find(pu) == s[pv].end())
                merge(pu,pv);
            else 
            {
                ans[cnt++]=tim;
                tim=0;
                init();
            }
        }
        else 
        {
            if(pu == pv)
            {
                ans[cnt++]=tim;
                tim=0;
                init();
            }
            else
            {
                s[pu].insert(pv);
                s[pv].insert(pu);
            }
        }
    }

    cout<<cnt<<endl;

    for(int i=0;i<cnt;i++)
        cout<<ans[i]<<endl;
    return 0;
}