树状数组复习

作者： 作者的头像   二助 ,  2020-03-03 00:50:20 ,  所有人可见 ,  阅读 1005

5


7

树状数组

1.PNG
2.png
3.png
4.png
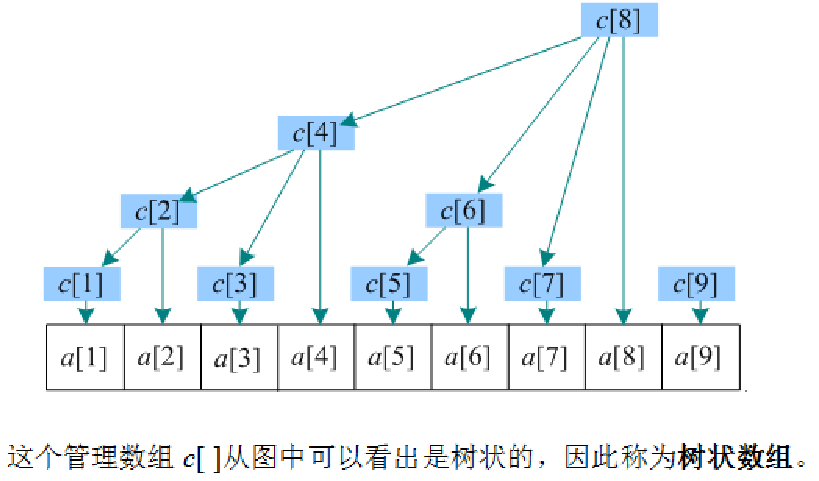
sum[9]=c[9]+c[8];
6.png

7.png
8.png
9.png
10.png

11.png
12.png
13.png
14.png

15.png
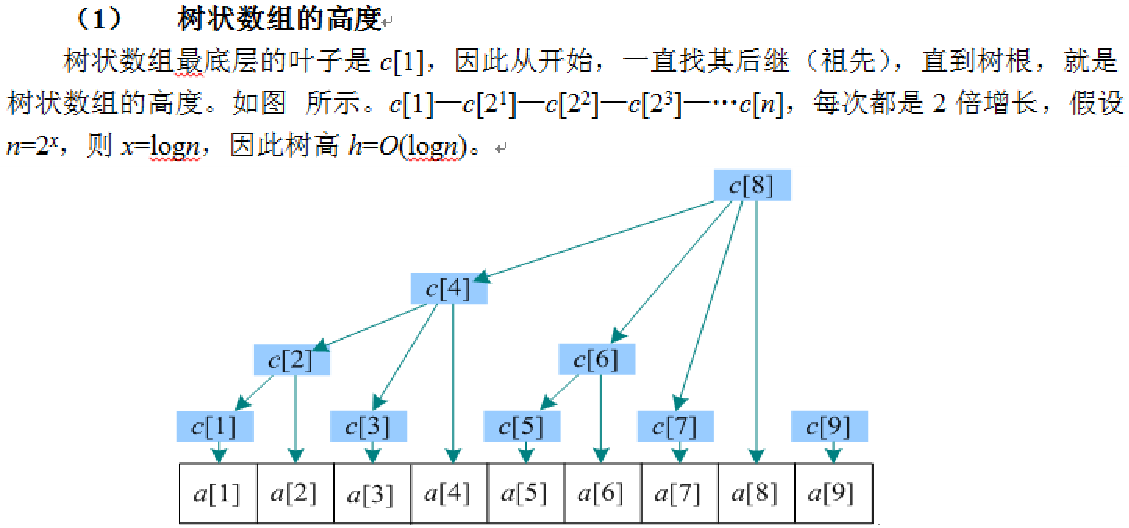
16.png
17.png 

#include<iostream>
#include<cstring>
using namespace std;
const int maxn=10000;
int n,a[maxn],c[maxn],s[maxn];

int lowbit(int i)//c[i]的区间长度 
{
    return (-i)&i;
}

void add(int i,int z)//a[i]加上z
{
    for(;i<=n;i+=lowbit(i))//直接后继，即父亲i+=lowbit(i)
        c[i]+=z;    
} 

int sum(int i)//求前缀和a[1]..a[i] 
{
    int s=0;
    for(;i>0;i-=lowbit(i))//直接前驱 i-=lowbit(i);
        s+=c[i];
    return s; 
}

int sum(int i,int j)//求区间和a[i]..a[j] 
{
    return sum(j)-sum(i-1); 
}

int main()
{
    memset(c,0,sizeof(c));
    cin>>n;
    for(int i=1;i<=n;i++)
    {
        cin>>a[i];
        add(i,a[i]);//加入树状数组 
    } 
    int x1,x2;
    cin>>x1;
    cout<<sum(x1)<<endl;
    cin>>x1>>x2;
    cout<<sum(x1,x2)<<endl;
    return 0;
}

18.png
19.png
20.png
21.png
22.png 

#include<iostream>
#include<cstring>
using namespace std;
const int maxn=10000;
int n,a[maxn][maxn],c[maxn][maxn];//二维树状数组 

int lowbit(int i)//区间长度 
{
    return (-i)&i;
}

void add(int x,int y,int z)//a[x][y]加上z
{
    for(int i=x;i<=n;i+=lowbit(i))
        for(int j=y;j<=n;j+=lowbit(j))
            c[i][j]+=z;
} 

int sum(int x,int y)//求左上角(1,1)到右下角(x,y)矩阵区间和 
{
    int s=0;
    for(int i=x;i>0;i-=lowbit(i))
        for(int j=y;j>0;j-=lowbit(j))
            s+=c[i][j];
    return s; 
}

int sum(int x1,int y1,int x2,int y2)//求左上角(x1,y1)到右下角(x2,y2)子矩阵区间和 
{
    return sum(x2,y2)-sum(x1-1,y2)-sum(x2,y1-1)+sum(x1-1,y1-1); 
}

int main()
{
    for(int i=1;i<=n;i++)
        memset(c[i],0,sizeof(c[i]));
    cin>>n;
    for(int i=1;i<=n;i++)
        for(int j=1;j<=n;j++)
        {
            cin>>a[i][j];
            add(i,j,a[i][j]);//加入树状数组 
        } 
    int x1,y1,x2,y2;
    cin>>x1>>y1;
    cout<<sum(x1,y1)<<endl;
    cin>>x1>>y1>>x2>>y2;
    cout<<sum(x1,y1,x2,y2)<<endl;
    return 0;
}

poj2352
统计x前面比它小的星星的个数。注意的是：给的点的坐标是从0开始的，树状数组下标为0的位置不可用，所以我们需要在输入x坐标时+1。

因为本题给出的数据就是已经按照y从小到大排好序的,也就是说，当前读到一个点的时候，当前点的y坐标肯定比已经读入的大，或者等于。就算是等于的话，也是x坐标比我当前点的x坐标小，所以我们每次只要算x坐标比我们小的就行了 。
23.png
24.png 

#include<cstdio>
using namespace std;
#define maxn 32010
int ans[maxn],tr[maxn];//等级统计，每个值的数量 
int n;

int lowbit(int x)
{
    return x&-x;
}

void add(int x,int c)//将第i个元素增加val，其后继也要增加
{
    for(int i=x;i<=maxn;i+=lowbit(i))//是x点的范围，注意不是星星的个数n 
        tr[i]+=c;//i的后继（父结点） 
}

int sum(int x)//前缀和 
{
    int res=0;
    for(int i=x;i;i-=lowbit(i))
        res+=tr[i];//i的前驱
    return res;
}

int main()
{
    scanf("%d",&n);
    int x,y;
    for(int i=0;i<n;i++)
    {
        scanf("%d%d",&x,&y);
        x++;
        ans[sum(x)]++;
        add(x,1);//x的数量c[x]增1,若是统计小于等于x的数量，则先执行add操作再查询 
    }
    for(int i=0;i<n;i++)
        printf("%d\n",ans[i]);
    return 0;
}

树状数组求逆序对

1）逆序数问题定义
给一个1~n的排列，求满足$i < j$且$a[i]>a[j]$的二元组对数，比如[4,2,1,5,3]这个序列，满足条件的二元组为{<4,2>, <4,1>, <4,3>, <2,1>, <5,3>}，故逆序数是5

2）树状数组求逆序数的原理
首先明确树状数组在此问题中维护信息是某个区间中数字出现的个数，sum(a[i])可求得[1, a[i]]的区间和，这恰好代表第i个数字前小于它的个数，，那么大于它的显然就有sum(n)-sum(a[i])个,然后将源数据按其原本顺序插入树状数组，第i个数字插入的方式为将树状数组的第a[i]位设为1，同时更新覆盖到它的父区间。

for (int i = 1; i <= n; i++) 
{
    ans += sum(n) - sum(a[i]);
    add(a[i], 1);
}

累加每步的结果后可得逆序数为5，用树状数组的好处在于add操作和sum的操作时间复杂度都为O(logn)，非常的巧妙

poj3067
由于x是从小到大排序的，假设当前我们在处理第k条边，那么第1~k-1条边的x必然是小于（等于时候暂且不讨论）第k条边的 x 的，那么前k-1条边中，与第k条边相交的边的y值必然大于yk的，所以此时我们只需要求出在前k-1条边中有多少条边的y值在区间[yk, M]即可,也就是求yk的逆序数，M为西岸城市个数，即y的最大值。

所以就将问题转化成区间求和的问题，树状数组解决。当两条边的x相同时，我们记这两条边的y值分别为ya，yb（ya<yb),我们先处理（x，ya），再处理（x，yb），原因很明显，因为当x相同时，这两条边是认为没有交点的，若先处理（x，yb），那么下次处理（x，ya）时，（x，ya）就会给（x，yb）增加一个逆序，也就是将这两条边做相交处理了。

#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int N=1010,M=1000010;
int tr[N];
int n,m,k;
struct Edge 
{
    int x, y;
    bool operator< (const Edge &W) const 
    {
        if(x == W.x)
            return y<W.y;
        else
            return x<W.x;
    }
}e[M];
typedef long long LL;

int lowbit(int x)
{
    return x&-x;
}

void add(int x)//加1操作，参数省略
{
    for(int i=x;i<=m;i+=lowbit(i))//y点有m个
        tr[i]++;
}

int sum(int x)
{
    int res=0;
    for(int i=x;i;i-=lowbit(i))
        res+=tr[i];
    return res;
}

int main()
{
    int T;
    scanf("%d",&T);
    for(int kase=1;kase<=T;kase++)
    {
        memset(tr,0,sizeof tr);
        scanf("%d%d%d",&n,&m,&k);
        for(int i=1;i<=k;i++)
            scanf("%d%d",&e[i].x,&e[i].y);
        sort(e+1,e+k+1);
        LL ans=0;
        for(int i=1;i<=k;i++)
        {
            ans+=sum(m)-sum(e[i].y);
            add(e[i].y);
        }
        printf("Test case %d: %lld\n",kase,ans);
    }
    return 0;
}

acwing241
25.PNG 

#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
typedef long long LL;
const int N = 200010;
int n;
int a[N];
int tr[N];
int bigger[N], lower[N];

int lowbit(int x)
{
    return x & -x;
}

void add(int x, int c)
{
    for (int i = x; i <= n; i += lowbit(i)) tr[i] += c;
}

int sum(int x)
{
    int res = 0;
    for (int i = x; i; i -= lowbit(i)) res += tr[i];
    return res;
}

int main()
{
    scanf("%d", &n);

    for (int i = 1; i <= n; i ++ ) scanf("%d", &a[i]);

    for (int i = 1; i <= n; i ++ )//从左向右扫
    {
        bigger[i] = sum(n) - sum(a[i]);//1~i-1有多少数大于y（y+1~n）
        lower[i] = sum(a[i]);//1~i-1有多少数小于y（1~y-1）
        add(a[i], 1);
    }

    memset(tr, 0, sizeof tr);
    LL res1 = 0, res2 = 0;
    for (int i = n; i; i -- )//从右向左扫
    {
        res1 += bigger[i] * (LL)(sum(n) - sum(a[i]));//i+1~n有多少数大于y
        res2 += lower[i] * (LL)(sum(a[i]));//i+1~n有多少数小于y
        add(a[i], 1);
    }

    printf("%lld %lld\n", res1, res2);

    return 0;
}

拓展应用

1.树状数组基本应用. 单点修改 + 区间查询

2.区间修改 + 单点查询

26.PNG
acwing242

#include<iostream>
using namespace std;
const int N=100010;
int a[N];
int n,m;
int tr[N];
typedef long long LL;

int lowbit(int x)
{
    return x&-x;
}

void add(int x,int c)
{
    for(int i=x;i<=n;i+=lowbit(i))
        tr[i]+=c;
}

int sum(int x)
{
    int res=0;
    for(int i=x;i;i-=lowbit(i))
        res+=tr[i];
    return res;
}

int main()
{
    cin>>n>>m;

    for(int i=1;i<=n;i++)
    {
        scanf("%d",&a[i]);
        add(i,a[i]-a[i-1]);
    }

    while(m--)
    {
        char op[2];
        scanf("%s",op);
        if(*op == 'C')
        {
            int l,r,d;
            scanf("%d%d%d",&l,&r,&d);
            add(l,d);
            add(r+1,-d);
        }
        else
        {
            int x;
            scanf("%d",&x);
            printf("%d\n",sum(x));
        }
    }
    return 0;
 }

3.区间修改 + 区间查询

acwing243
27.PNG
28.PNG 

//区间加
//区间和
#include<iostream>
using namespace std;
typedef long long LL;
const int N=100010;
int n,m;
int a[N];
LL tr1[N];//维护b[i]的前缀和
LL tr2[N];//维护b[i]*i的前缀和

int lowbit(int x)
{
    return x&-x;
}

void add(LL tr[],int x,LL c)
{
    for(int i=x;i<=n;i+=lowbit(i))
        tr[i]+=c;
}

LL sum(LL tr[],int x)
{
    LL res=0;
    for(int i=x;i;i-=lowbit(i))
        res+=tr[i];
    return res;
}

LL prefix_sum(int x)
{
    return sum(tr1,x)*(x+1)-sum(tr2,x);
}

int main()
{
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++)
        scanf("%d",&a[i]);
    for(int i=1;i<=n;i++)
    {
        int b=a[i]-a[i-1];//最大为1e9
        add(tr1,i,b);
        add(tr2,i,(LL)i*b);
    }

    while(m--)
    {
        char op[2];
        int l,r,d;
        scanf("%s%d%d",op,&l,&r);
        if(*op == 'Q')
            printf("%lld\n",prefix_sum(r)-prefix_sum(l-1));
        else
        {
            scanf("%d",&d);
            add(tr1,l,d);
            add(tr1,r+1,-d);
            add(tr2,l,l*d);
            add(tr2,r+1,(r+1)*-d);
        }
    }
    return 0;
}

acwing244
我们发现,如果说第K头牛的前面有Ak头牛比它矮,那么它的身高Hk就是数值1 n中第Ak+1小的没有在$H_{k+1},H_{k+2},…,H_{n}$中出现过的数
所以说,我们需要建立一个长度为n的01序列b,刚开始都是1,然后n到1倒序扫描每一个$A_i$,对于每个$A_i$
执行查询和修改操作.
也就是说这道题目的题意就是让我们,动态维护一个01序列,支持查询第k个1所在的位置,以及修改序列中的一个数值

#include<iostream>
using namespace std;
const int N=100010;
int h[N];
int n;
int tr[N];
int ans[N];

int lowbit(int x)
{
    return x&-x;
}

void add(int x,int c)
{
    for(int i=x;i<=n;i+=lowbit(i))
        tr[i]+=c;
}

int sum(int x)
{
    int res=0;
    for(int i=x;i;i-=lowbit(i))  
        res+=tr[i];
    return res;
}

int main()
{
    cin>>n;
    for(int i=2;i<=n;i++)
        cin>>h[i];

    for(int i=1;i<=n;i++)   
        tr[i]=lowbit(i);//相当于add(i,1);

    for(int i=n;i;i--)
    {
        int k=h[i]+1;
        int l=1,r=n;
        while(l<r)
        {
            int mid=l+r>>1;
            if(sum(mid) >= k)
                r=mid;
            else
                l=mid+1;
        }
        ans[i]=l;
        add(l,-1);
    }

    for(int i=1;i<=n;i++)
        cout<<ans[i]<<endl;
    return 0;
}

poj1195
29.PNG 

#include<cstdio>
#include<cstring>
#define maxn 1050
#define lowbit(x) (x)&(-x)
int c[maxn][maxn],n;

void add(int x,int y,int z)//单点更新 
{
    for(int i=x;i<=n;i+=lowbit(i))
        for(int j=y;j<=n;j+=lowbit(j))
            c[i][j]+=z;
}

int sum(int x,int y)//区间和：左上角(1,1)到右下角(x,y)矩阵区间和 
{
    int s=0;
    for(int i=x;i>0;i-=lowbit(i))
        for(int j=y;j>0;j-=lowbit(j))
            s+=c[i][j];
    return s;
}

int sum(int x1,int y1,int x2,int y2)//求左上角(x1,y1)到右下角(x2,y2)子矩阵区间和 
{
    return sum(x2,y2)-sum(x1-1,y2)-sum(x2,y1-1)+sum(x1-1,y1-1);
}

int main()
{
    int opt,x,y,a,l,b,r,t;
    while(scanf("%d",&opt)!=EOF)
    {
        if(opt==3) break;
        if(opt==0)
        {
            scanf("%d",&n);
            memset(c,0,sizeof(c));
        }
        else if(opt==1)
        {
            scanf("%d%d%d",&x,&y,&a);
            ++x;++y;
            add(x,y,a);
        }
        else
        {
            scanf("%d%d%d%d",&l,&b,&r,&t);
            ++l,++b,++r,++t;
            printf("%d\n",sum(l,b,r,t));
        }
    }
    return 0;
}

poj3321
30.png
31.png
32.png
33.png 

#include<stdio.h>
#include<iostream>
#include<algorithm>
#include<cstring>
#include<cmath>
using namespace std;
const int maxn=1e5+10;
int n,q;
int c[maxn];
int a[maxn];
int L[maxn],R[maxn];
int head[maxn];
int cnt;
int dfn;
struct edge{
    int u,v;
    int next;
}E[2*maxn];

void adde(int u,int v)
{
    E[++cnt].u=u;
    E[cnt].v=v;
    E[cnt].next=head[u];
    head[u]=cnt;
}

int lowbit(int x)
{
    return x&(-x);
}

void add(int x,int v)
{
    for(int i=x;i<=n;i+=lowbit(i))
        c[i]+=v;
}

int sum(int x)
{
    int ans=0;
    for(int i=x;i;i-=lowbit(i))
    {
        ans+=c[i];
    }
    return ans;
}


void dfs(int u,int fa)
{
    L[u]=++dfn;
    for(int i=head[u];i;i=E[i].next)
    {
        int v=E[i].v;
        if(v==fa) continue;
        dfs(v,u);
    }
    R[u]=dfn;
}

int main()
{
    scanf("%d",&n);
    int u,v;
    for(int i=1;i<=n;i++)
    {
        c[i]=lowbit(i);
        a[i]=1;
    }
    for(int i=1;i<n;i++)
    {
        scanf("%d%d",&u,&v);
        adde(u,v);
    }
    dfs(1,-1);
//  for(int i=1;i<=n;i++)//测试dfs序列 
//      printf("--%d %d\n",L[i],R[i]);
//      printf("\n");   
    scanf("%d",&q);
    char op[10];
    for(int i=1;i<=q;i++)
    {
        scanf("%s%d",op,&v);
        if(op[0]=='C')
        {
            int j=L[v];
            if(a[j])//由于每个节点的dfn编号就是它的左值，所以直接修改左节点
                add(j,-1);
            else
                add(j,1);
            a[j]^=1;
        }
        else
        {
            int s1=sum(R[v]);
            int s2=sum(L[v]-1);
            printf("%d\n",s1-s2);
        }
    }
    return 0;
}

2 评论

用户头像
妙WA种子_   2021-05-14 11:35         踩      回复

我想问一下 c[ i ] 前驱那里。 对于c[i]， c[ i - lowbit( i ) ] 不是 c[i] 的子结点， 不过它们都是 c[ i + lowbit( i ) ] 的子节点，然后这个前驱是 c[ i ] 左面紧邻的。是这个意思吗？

用户头像
妙WA种子_   2021-05-14 11:31         踩      回复

Orz。大佬的分享很整洁。