链表结构

• 1、单链表的定义
  ①类型和变量的说明

struct Node{
    int data;
    Node *next;
};
Node *p;

②申请存储单元

p=new Node;//动态申请、空间大小由指针变量的基本类型决定

③指针变量的赋值

指针变量名=NULL;//初始化，暂时不指向任何存储单元

• 2、单链表的结构、建立、输出
  
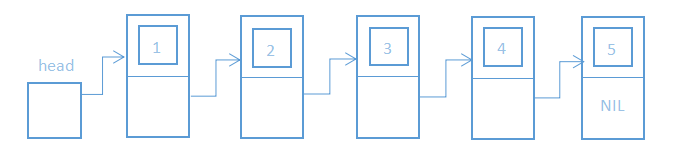
  下面是建立并输出单链表的程序。

#include<bits/stdc++.h>
using namespace std;

struct Node{
    int data;
    Node *next;
};
Node *head,*p,*r;

int x;

int main(){
    cin>>x;
    head=new Node;//申请头结点
    r=head;

    while(x!=-1){//读入的数非-1
        p=new Node;//否则，申请一个新节点

        p->data=x;
        p->next=NULL;
        r->next=p;//把新节点链接到前面的链表中，实际上r是p的直接前趋

        r=p;//尾指针后移一个
        cin>>x;
    }

    p=head->next;//头指针没有数据，只要从第一个结点开始就可以了

    while(p->next!=NULL){
        cout<<p->data<<" ";
        p=p->next;
    }
    cout<<p->data<<endl;//最后一格结点的数据单独输出，也可以改用do-while循环

    system("pause");
}

• 3、单链表的操作
  ①查找“数据域满足一定条件的结点”

p=head->next;
while((p->data!=x)&&(p->next!=NULL))
    p=p->next;//找到第一个就结束
if(p->data==x)
    找到了就处理;
else
    输出不存在;

如果想找到所有满足条件的结点，则修改如下：

p=head->next;
while(p->next!=NULL){//一个一个判断
    if(p->data==x)//找到一个处理一个
    p=p->next;
}

②取出单链表的第i个结点的数据域

void get(Node *head,int i){
    Node *p;int j;
    p=head->next;
    j=1;

    while((p!=NULL)&&(j<i)){
        p=p->next;
        j++;
    }

    if((p!=NULL)&&(j==i))
        cout<<p->data;
    else 
        cout<<"i not exsit!";
}

③插入一个结点在单链表中去

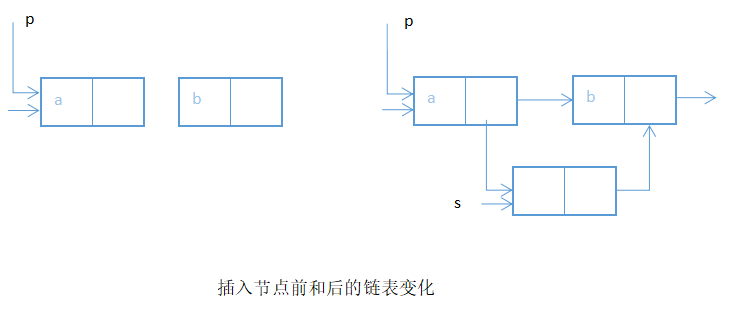
void insert(Node *head,int i,int x){//插入x到第i个元素之前
    Node *p,*s;int j;
    p=head;j=0;

    while((p!=NULL)&&(j<i-1)){//寻找i-1个结点，插在它的后面
        p=p->next;
        j++;
    }

    if(p==NULL)
        cout<<"no this position!";
    else{//插入
        s=new Node;

        s->data=x;
        s->next=p->next;
        p->next=s;
    }
}

④删除单链表中的第i个结点

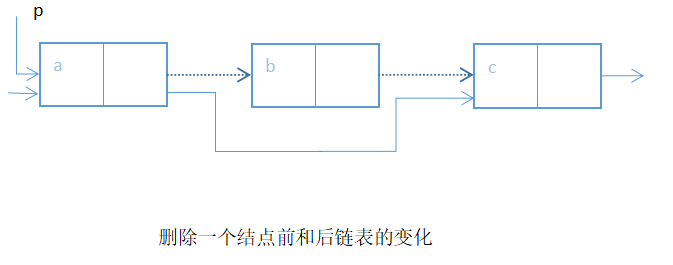
void delete(Node *head,int i){//删除第i个元素
    Node *p,*s;int j;
    p=head;j=0;

    while((p->next!=NULL)&&(j<i-1)){
        p=p->next;
        j++;
    } //p指向第i-1个结点

    if(p->next==NULL)
        cout<<"no this position!";
    else{
        s=p->next;
        p->next=p->next->next;//或p->next=s->next
        free(s);
    }
}

⑤求单链表的实际长度

int len(Node *head){
    int n=0;
    p=head;

    while(p!=NULL){
        n++;
        p=p->next;
    }

    return n;
}

• 4、双向链表
  【数据结构的定义】

struct node{
    int data;
    node *pre,*next;//pre指向前趋，next指向后继
}
node *head,*p,*q,*r;

下面是双向链表的插入和删除过程

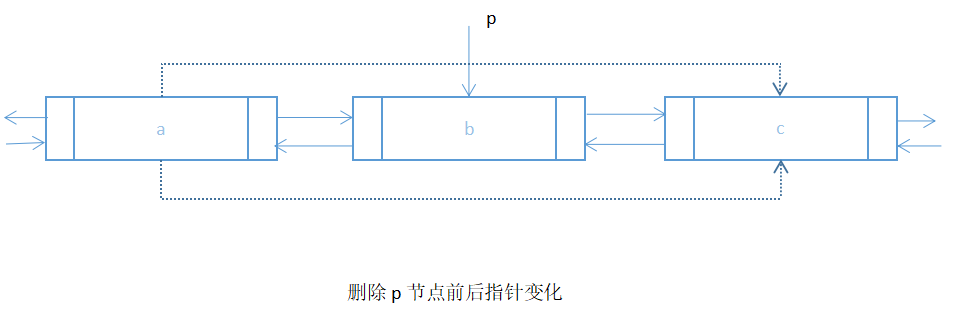
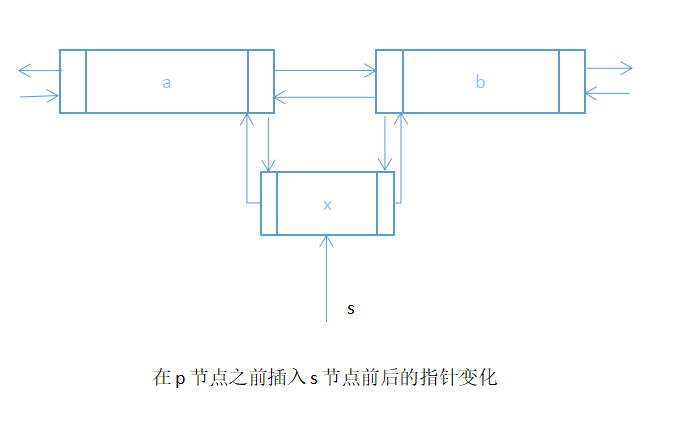
void insert(node *head,int i,int x){//在双向链表的第i个结点之前插入x
    node *s,*p;
    int j;

    s=new node;
    s->data=x;

    p=head;j=0;

    while((p->next!=NULL)&&(j<i)){
        p=p->next;
        j++;
    }//p指向第i个结点

    if(p==NULL)
        cout<<"no this position!";
    else{//将结点s插入到结点p之前
        s->pre=p->pre;//将s的前趋指向p的前趋
        p->pre=s;//将s作为p的新前趋
        s->next=p;//将s的后继指向p
        p->pre->next=s;//将p的本来前趋结点的后继指向s
    }
}

void delete(node *head,int i){//删除双向链表的第i个结点
    int j;node *p;
    p=head;j=0;

    while((p->next!=NULL)&&(j<i)){
        p=p->next;
        j++;
    }//p指向第i个结点

    if(p==NULL)
        cout<<"no this position!";
    else{//将结点p删除
        p->pre->next=p->next;//p的前趋结点的后继赋值为p的后继
        p->next->pre=p->pre;//p的后继结点的前趋赋值为p的前趋
    }
}

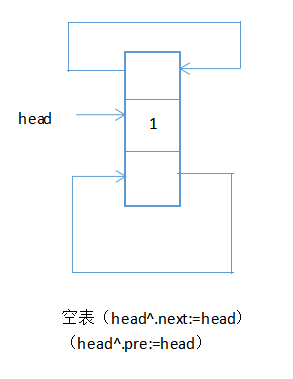
• 5、循环链表
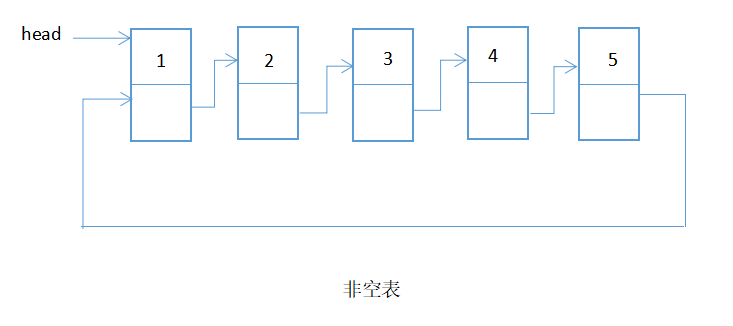
  单项循环链表：最后一个结点的指针指向头结点。
  
  
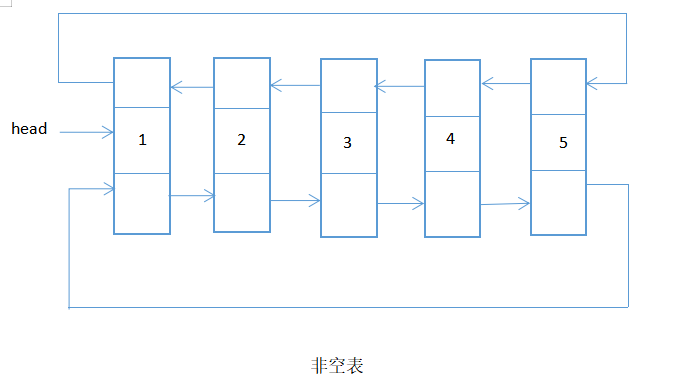
  双向循环链表：最后一个结点的指针指向头结点，且头结点的前趋指向最后一个结点。
  
  
• 6、循环链表的应用举例
  例：约瑟夫环问题

#include<bit/stdc++.h>
using namespace std;

struct node{
    int d;
    node *next;
};

int n,m;
node *head,*p,*r;

int main(){
    int i,j,k,l;
    cin>>n>>m;
    head=new node;
    hesd->d=1;head->next=NULL;r=head;

    for(i=2;i<=n;i++){
        p=new node;

        p->d=i;
        p->next=NULL;
        r->next=p;

        r=p;
    }

    r->next=head;r=head;

    for(i=1;i<=n;i++){
        for(j=1;j<=m-2;j++)
            r=r->next;

        cout<<r->next->d<<" ";

        r->next=r->next->next;
        r=r->next;
    }
}

输入：8 5
输出：5 2 8 7 1 4 6 3