带懒标记线段树

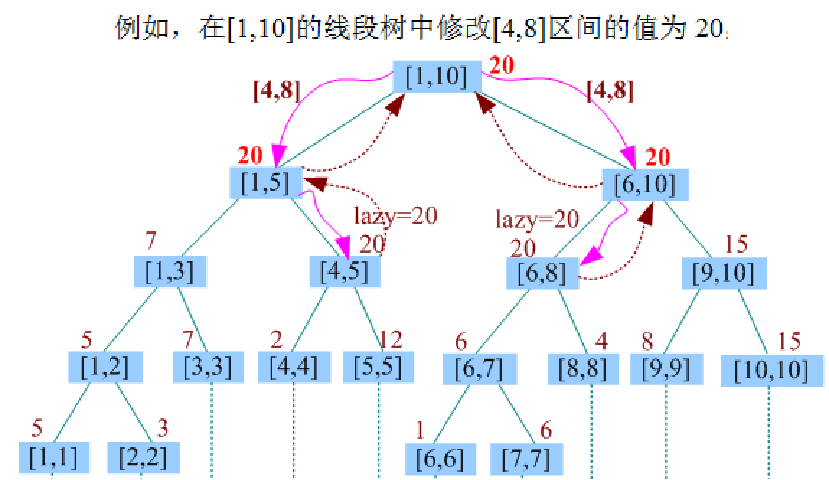
struct node//结点
{
int l,r,mx,lz;//l,r表示区间左右端点,mx表示区间[l,r]的最值,lz为懒标记
}tree[maxn*4]; //树结点存储数组
void lazy(int k,int v)
{
tree[k].mx=v;//更新最值
tree[k].lz=v;//做懒标记
}
void pushdown(int k)//向下传递懒标记
{
lazy(2*k,tree[k].lz);//传递给左孩子
lazy(2*k+1,tree[k].lz);//传递给右孩子
tree[k].lz=-1;//清除自己的懒标记
}
void update(int k,int l,int r,int v)//将区间[l..r]修改更新为v
{
if(tree[k].l>=l&&tree[k].r<=r)//找到该区间
return lazy(k,v);//更新并做懒标记
if(tree[k].lz!=-1)
pushdown(k);//懒标记下移
int mid,lc,rc;
mid=(tree[k].l+tree[k].r)/2;//划分点
lc=k*2; //左孩子存储下标
rc=k*2+1;//右孩子存储下标
if(l<=mid)
update(lc,l,r,v);//到左子树更新
if(r>mid)
update(rc,l,r,v);//到右子树更新
tree[k].mx=max(tree[lc].mx,tree[rc].mx);//返回时修改更新最值
}

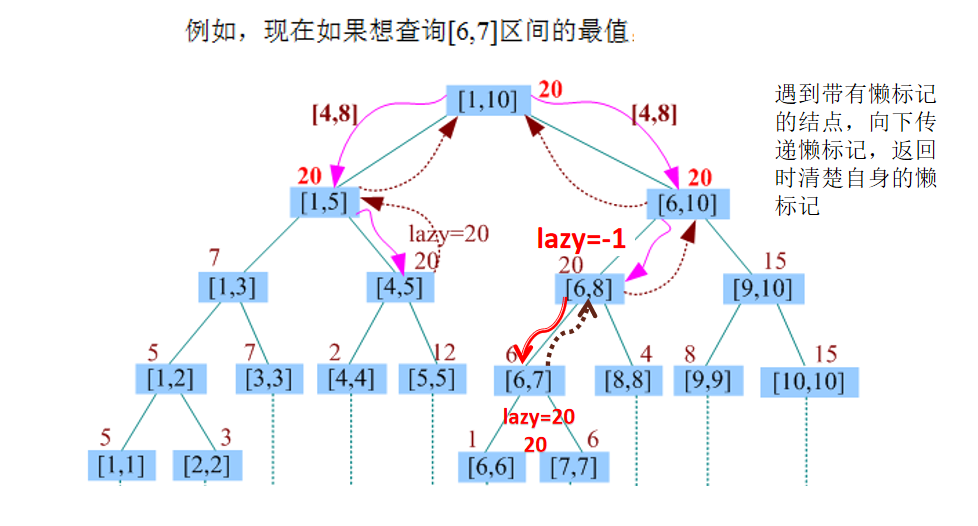
int query(int k,int l,int r)//求区间[l..r]的最值
{
int Max=-inf;
if(tree[k].l>=l&&tree[k].r<=r)//找到该区间
return tree[k].mx;
if(tree[k].lz!=-1)
pushdown(k);//懒标记下移
int mid,lc,rc;
mid=(tree[k].l+tree[k].r)/2;//划分点
lc=k*2; //左孩子存储下标
rc=k*2+1;//右孩子存储下标
if(l<=mid)
Max=max(Max,query(lc,l,r));//到左子树查询
if(r>mid)
Max=max(Max,query(rc,l,r));//到右子树查询
return Max;
}

打印线段树
void print(int k)
{
if(tree[k].mx)
{
cout<<k<<"\t"<<tree[k].l<<"\t"<<tree[k].r<<"\t"<<tree[k].mx<<"\t"<<endl;
print(k<<1);
print((k<<1)+1);
}
}
例题
问题1:(单点修改+区间和)
有一个长度为 n 的序列,a[1], a[2], …, a[n]。
现在执行 m 次操作,每次可以执行以下两种操作之一:
1. 将下标在区间 [l, r] 的数都修改为 v(v>0)。
2. 询问一个下标区间 [l, r] 中所有数的和。
如果把区间修改拆成 r - l + 1 个单点修改,甚至不如模拟。
我们希望区间修改和区间查询一样,先把区间分成线段树上的
若干个区间。然后分别修改这几个区间。
对于[l, mid]:tag[x * 2] = tag[x], sum[x * 2] = (mid - l + 1) * tag[x];
对于[mid+1, r]:tag[x * 2 + 1] = tag[x], sum[x * 2 + 1] = (r - mid) * tag[x]
然后把 tag[x] 置为 0,表示这个点上已经没有待下传的标记了。对于查询和修改操作,都需要检查当前节点是否需要下传标记
为了方便,我们定义 ls, rs 分别为左右子树的编号:
#define ls (x << 1)
#define rs (x << 1 | 1)
更新函数:
void update(int x){
sum[x] = sum[ls] + sum[rs];
}
标记下传函数:
void down(int l, int r, int x){
int mid = (l + r) >> 1;
if (tag[x] > 0){
tag[ls] = tag[rs] = tag[x];
sum[ls] = (mid - l + 1) * tag[x];
sum[rs] = (r - mid) * tag[x];
tag[x] = 0;
}
}
修改[A, B]区间改为 v:
void change(int A, int B, int v, int l, int r, int x) {
if (A <= l && r <= B) {
tag[x] = v;
sum[x] = v * (r - l + 1);
return;
}
down(l, r, x); // 在继续修改之前,先检查是否要下传标记
int mid = (l + r) >> 1;
if (A <= mid) change(A, B, v, l, mid, ls);
if (mid < B) change(A, B, v, mid + 1, r, rs);
update(x); // 回溯的时候要更新每个节点的sum,因为子节点的值改变了
}
查询[A, B]的区间和
int query(int A, int B, int l, int r, int x) {
if (A <= l && r <= B)
return sum[x];
down(l, r, x); // 在继续查询之前,先检查是否要下传标记
int mid = (l + r) >> 1, ret = 0;
if (A <= mid) ret += query(A, B, l, mid, ls);
if (mid < B) ret += query(A, B, mid + 1, r, rs);
return ret;
}
这种到需要的时候才进行标记下传的方法,使我们整体处
理的时间复杂度仍然维持在 O(log2n)
问题2:(区间修改+区间求和)
有一个长度为 n 的序列,a[1], a[2], …, a[n]。现在执行
m 次操作,每次可以执行以下两种操作之一:
1. 将下标在区间 [l, r] 的数都加上 v。
2. 询问一个下标区间 [l, r] 中所有数的和
和区间修改成一个数类似,我们只需要改变 tag 的定义:
tag 表示当前节点代表的区间每个数都要加上的值
标记下传函数:
void down(int l, int r, int x){
int mid = (l + r) >> 1;
if (tag[x] != 0) {
tag[ls] += tag[x];
tag[rs] += tag[x];
sum[ls] += (mid - l + 1) * tag[x];
sum[rs] += (r - mid) * tag[x];
tag[x] = 0;
}
}
对[A, B]中的每个数都加上 v
void add(int A, int B, int v, int l, int r, int x) {
if (A <= l && r <= B) {
tag[x] += v;
sum[x] += v * (r - l + 1);
return;
}
down(l, r, x); // 在继续修改之前,先检查是否要下传标记
int mid = (l + r) >> 1;
if (A <= mid) add(A, B, v, l, mid, ls);
if (mid < B) add(A, B, v, mid + 1, r, rs);
update(x); // 回溯的时候要更新每个节点的sum,因为子节点的值改变了
}
#include<iostream>
#include<algorithm>
#include<algorithm>
using namespace std;
const int N=1e5+10;
#define lc u<<1
#define rc u<<1|1
typedef long long LL;
struct Node
{
int l,r;
LL sum;
int tag;
}tr[N*4];
int w[N];
int n,m;
void pushup(int u)
{
tr[u].sum=tr[lc].sum+tr[rc].sum;
}
void build(int u,int l,int r)
{
if(l == r)
{
tr[u]={l,l,w[l],0};
return;
}
tr[u]={l,r};
int mid=l+r>>1;
build(lc,l,mid);
build(rc,mid+1,r);
pushup(u);
}
void pushdown(int u)
{
if(tr[u].tag)
{
tr[lc].sum+=(LL)(tr[lc].r-tr[lc].l+1)*tr[u].tag;
tr[lc].tag+=tr[u].tag;
tr[rc].sum+=(LL)(tr[rc].r-tr[rc].l+1)*tr[u].tag;
tr[rc].tag+=tr[u].tag;
tr[u].tag=0;
}
}
void modify(int u,int l,int r,int d)
{
if(l<= tr[u].l && tr[u].r <=r)
{
tr[u].sum+=(LL)(tr[u].r-tr[u].l+1)*d;
tr[u].tag+=d;
return;
}
pushdown(u);
int mid=tr[u].l+tr[u].r>>1;
if(l <= mid)
modify(lc,l,r,d);
if(r > mid)
modify(rc,l,r,d);
pushup(u);
}
LL query(int u,int l,int r)
{
if(tr[u].l >= l && tr[u].r <= r)
return tr[u].sum;
pushdown(u);
int mid=tr[u].l+tr[u].r>>1;
LL sum=0;
if(l <= mid)
sum+=query(lc,l,r);
if(r > mid)
sum+=query(rc,l,r);
return sum;
}
int main()
{
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)
scanf("%d",&w[i]);
build(1,1,n);
while(m--)
{
char op[2];
int l,r,d;
scanf("%s%d%d",op,&l,&r);
if(*op == 'C')
{
scanf("%d",&d);
modify(1,l,r,d);
}
else
printf("%lld\n",query(1,l,r));
}
return 0;
}
问题3:(区间修改+区间最值查询)
有一个长度为 n 的序列,a[1], a[2], …, a[n]。现在执行
m 次操作,每次可以执行以下两种操作之一:
1. 将下标在区间 [l, r] 的数都加上 v。
2. 询问一个下标区间 [l, r] 中所有数的最小值。
和区间修改成一个数类似,我们只需要改变 tag 的定义:
tag 表示当前节点代表的区间每个数都要加上的值。
Min 表示当前节点代表的区间的最小值。
更新信息函数:
void update(int x){
Min[x] = min(Min[ls], Min[rs]);
}
标记下传函数:
void down(int l, int r, int x){
int mid = (l + r) >> 1;
if (tag[x] != 0){
tag[ls] += tag[x];
tag[rs] += tag[x];
Min[ls] += tag[x];
Min[rs] += tag[x];
tag[x] = 0;
}
}
对[A, B]中的每个数都加上 v
void add(int A, int B, int v, int l, int r, int x) {
if (A <= l && r <= B) {
tag[x] += v;
Min[x] += v;
return;
}
down(l, r, x); // 在继续修改之前,先检查是否要下传标记
int mid = (l + r) >> 1;
if (A <= mid) add(A, B, v, l, mid, ls);
if (mid < B) add(A, B, v, mid + 1, r, rs);
update(x); // 回溯的时候要更新每个节点的sum,因为子节点的值改变了
}
查询[A, B]的最小值
int query(int A, int B, int l, int r, int x) {
if (A <= l && r <= B)
return Min[x];
down(l, r, x); // 在继续查询之前,先检查是否要下传标记
int mid = (l + r) >> 1, ret = 0x3F3F3F3F;
if (A <= mid) ret = min(ret, query(A, B, l, mid, ls));
if (mid < B) ret = min(ret, query(A, B, mid + 1, r, rs));
return ret;
}
问题4:(区间修改+区间最值个数)
有一个长度为 n 的序列,a[1], a[2], …, a[n]。现在执行
m 次操作,每次可以执行以下两种操作之一:
1. 将下标在区间 [l, r] 的数都加上 v。
2. 询问一个下标区间 [l, r] 中所有数的最小值的个数。
和区间修改成一个数类似,我们只需要改变 tag 的定义:
tag 表示当前节点代表的区间每个数都要加上的值。
Min 表示当前节点代表的区间的最小值。
cnt 表示当前节点代表的区间的最小值的个数
更新信息函数:
void update(int x){
if (Min[ls] == Min[rs]){
Min[x] = Min[ls];
cnt[x] = cnt[ls] + cnt[rs];
}
else {
if (Min[ls] < Min[rs])
Min[x] = Min[ls], cnt[x] = cnt[ls];
else
Min[x] = Min[rs], cnt[x] = cnt[rs];
} }
标记下传函数:
// 此处 cnt 不用改变
void down(int l, int r, int x){
int mid = (l + r) >> 1;
if (tag[x] != 0){
tag[ls] += tag[x];
tag[rs] += tag[x];
Min[ls] += tag[x];
Min[rs] += tag[x];
tag[x] = 0;
}
}
对[A, B]中的每个数都加上 v
void add(int A, int B, int v, int l, int r, int x) {
if (A <= l && r <= B) {
tag[x] += v;
Min[x] += v;
return;
}
down(l, r, x); // 在继续修改之前,先检查是否要下传标记
int mid = (l + r) >> 1;
if (A <= mid) add(A, B, v, l, mid, ls);
if (mid < B) add(A, B, v, mid + 1, r, rs);
update(x); // 回溯的时候要更新每个节点的sum,因为子节点的值改变了
}
查询[A, B]的最小值
pair<int,int> query(int A, int B, int l, int r, int x) {
if (A <= l && r <= B)
return make_pair(Min[x], cnt[x]);
down(l, r, x); // 在继续查询之前,先检查是否要下传标记
int mid = (l + r) >> 1, ret = make_pair(0x3F3F3F3F, 0);
if (A <= mid)
ret = min(ret, query(A, B, l, mid, ls));
if (mid < B){
pair<int,int> tmp = min(ret, query(A, B, mid + 1, r, rs));
if (tmp.first == ret.first)
ret.second += tmp.second;
else if(tmp.first < ret.first)
ret = tmp; }
return ret;
}
如果要用线段树维护一个数据结构,一定要想清楚怎么实现update函数和down函数。也就是如何合并两个子树的信息,如何解决标记下传。
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
#define lc u<<1
#define rc u<<1|1
const int N=100010;
struct Node
{
int l,r;
int mx,tag;
}tr[N<<2];
int w[N];
int n,m;
void pushup(int u)
{
tr[u].mx=max(tr[lc].mx,tr[rc].mx);
}
void pushdown(int u)
{
if(tr[u].tag)
{
tr[lc].mx=tr[u].mx;
tr[lc].tag=tr[u].tag;
tr[rc].mx=tr[u].mx;
tr[rc].tag=tr[u].tag;
tr[u].tag=0;
}
}
int gcd(int a,int b)
{
return b? gcd(b,a%b) : a;
}
void build(int u,int l,int r)
{
if(l == r)
{
tr[u]={l,r,w[l],w[l]};
return;
}
tr[u]={l,r};
int mid=l+r>>1;
build(lc,l,mid);
build(rc,mid+1,r);
pushup(u);
}
void modify1(int u,int l,int r,int v)
{
if(l <=tr[u].l && tr[u].r <= r)
{
tr[u].mx=v;
tr[u].tag=v;
return;
}
pushdown(u);
int mid=tr[u].l+tr[u].r>>1;
if(l <= mid)
modify1(lc,l,r,v);
if(r > mid)
modify1(rc,l,r,v);
pushup(u);
}
void modify2(int u,int l,int r,int v)
{
if(tr[u].mx <= v)
return;
if(l <= tr[u].l && tr[u].r <= r)
{
if(tr[u].tag)
{
tr[u].tag=gcd(tr[u].tag,v);
tr[u].mx=tr[u].tag;
return;
}
}
pushdown(u);
int mid=tr[u].l+tr[u].r>>1;
if(l <= mid)
modify2(lc,l,r,v);
if(r > mid)
modify2(rc,l,r,v);
pushup(u);
}
void print(int u,int l,int r)
{
if(l == r)
{
printf("%d ",tr[u].tag);
return;
}
pushdown(u);//打印叶子结点,懒标记要下传!
int mid=l+r>>1;
print(lc,l,mid);
print(rc,mid+1,r);
}
int main()
{
int t;
scanf("%d",&t);
while(t--)
{
scanf("%d",&n);
for(int i=1;i<=n;i++)
scanf("%d",&w[i]);
build(1,1,n);
scanf("%d",&m);
while(m--)
{
int t,a,b,c;
scanf("%d%d%d%d",&t,&a,&b,&c);
if(t == 1)
modify1(1,a,b,c);
else
modify2(1,a,b,c);
}
print(1,1,n);
printf("\n");
}
return 0;
}
#include<iostream>
#include<algorithm>
#include<cstring>
#include<cstdio>
using namespace std;
#define lc u<<1
#define rc u<<1|1
const int N=100010;
struct Node
{
int l,r;
int tag;
}tr[N<<2];
int n,m,k;
bool ans[35];
void pushup(int u)
{
if(tr[lc].tag == tr[rc].tag)
tr[u].tag=tr[lc].tag;
}
void pushdown(int u)
{
if(tr[u].tag)
{
tr[lc].tag=tr[rc].tag=tr[u].tag;
tr[u].tag=0;
}
}
void build(int u,int l,int r)
{
tr[u]={l,r};
if(l == r)
return ;
int mid=l+r>>1;
build(lc,l,mid);
build(rc,mid+1,r);
}
void modify(int u,int l,int r,int d)
{
if(l <= tr[u].l && tr[u].r <= r)
{
tr[u].tag=d;
return;
}
pushdown(u);
int mid=tr[u].l+tr[u].r>>1;
if(l <= mid)
modify(lc,l,r,d);
if(r > mid)
modify(rc,l,r,d);
pushup(u);
}
void query(int u,int l,int r)
{
if(tr[u].tag)
{
ans[tr[u].tag]=true;
return;
}
int mid=tr[u].l+tr[u].r>>1;
if(l <= mid)
query(lc,l,r);
if(r > mid)
query(rc,l,r);
}
void print(int u)
{
if(tr[u].tag)
{
cout<<"--"<<u<<' '<<tr[u].l<<' '<<tr[u].r<<' '<<tr[u].tag<<endl;
print(lc);
print(rc);
}
}
int main()
{
scanf("%d%d%d",&n,&k,&m);
build(1,1,n);
tr[1].tag=1;
while(m--)
{
char op[2];
int l,r,d;
scanf("%s%d%d",op,&l,&r);
if(*op == 'C')
{
scanf("%d",&d);
modify(1,l,r,d);
}
else
{
memset(ans,0,sizeof ans);
int tot=0;
query(1,l,r);
for(int i=1;i<=30;i++)
if(ans[i])
tot++;
printf("%d\n",tot);
}
//print(1);
}
return 0;
}
poj2528
有一面墙,这面墙被等分为了1e7个小区间。现在要按顺序往这面墙上贴𝑛张海报,编号为𝑖的海报会覆盖标号从𝑙𝑖到𝑟𝑖的一段连续区间。问最后有多少海报能被露出来。
首先为什么只有在两个相邻大于1的数之间插入一个值就能防止因为离散放缩后导致的区间覆盖问题?
我们拿
1 10
1 4
6 10
这个常例来说
因为我们在离散化的时候只关心相对大小,所以这个6就是4之后的一个数,但是我们显然知道这样覆盖了5这个区间
我们在相邻大于1的数之间插入一个数,不管这个数是多大,只要他比前面的数大比后面的数小。我们都能够在离散化后的区间中模拟出来真实区间的间隔,并且我们不关心这个间隙有多大
只需要存在间隙,我们就能模拟成真实的情况,因为离散后的区间一定会被间隔开,所以这个数可以是任何数,例如两个数的平均值,或者是大数-1
而相邻差1的数,他在真实的区间中本来也就是相邻的,所以无需这种操作
code
按道理我们这有个pushup操作,但是本题并不需要根据儿子节点来更新父亲节点也能做
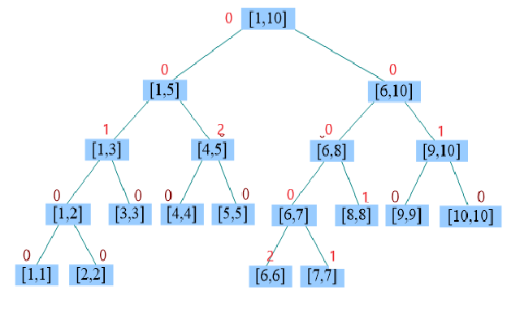
这个询问和普通线段树的询问略有不同 如果当前区间懒标记存在,说明这个区间是染色的,将染色的区间编号记录下来,若某段区间被覆盖的话,该区间的lazytag会更新为覆盖它的区间编号,统计答案时只需统计编号为true的区间即可。
扫描线
acwing247
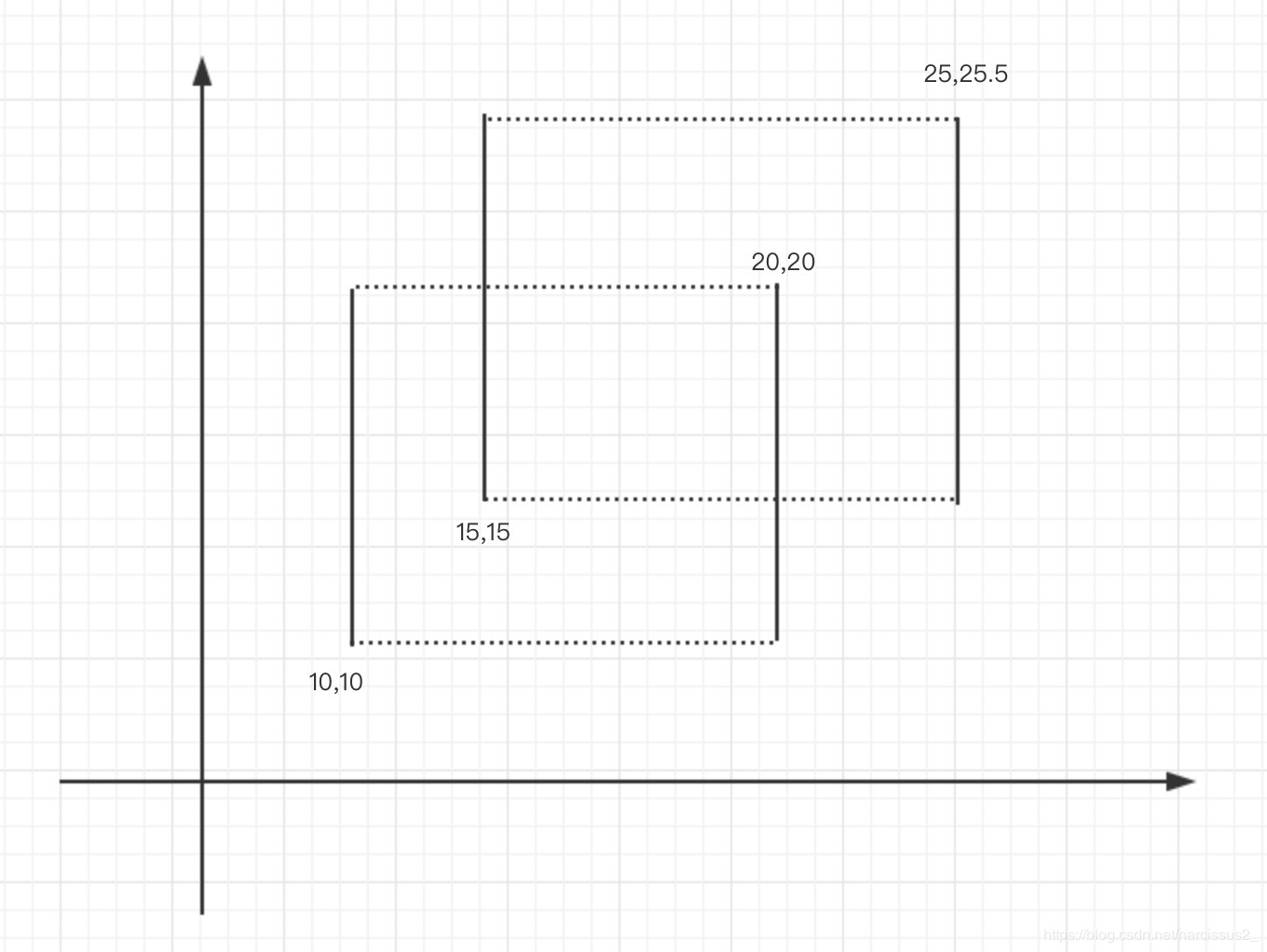
这道题最主要就是让我们求解矩形面积并,求解矩形面积并如果不用任何优化方式,那就是这么算的。
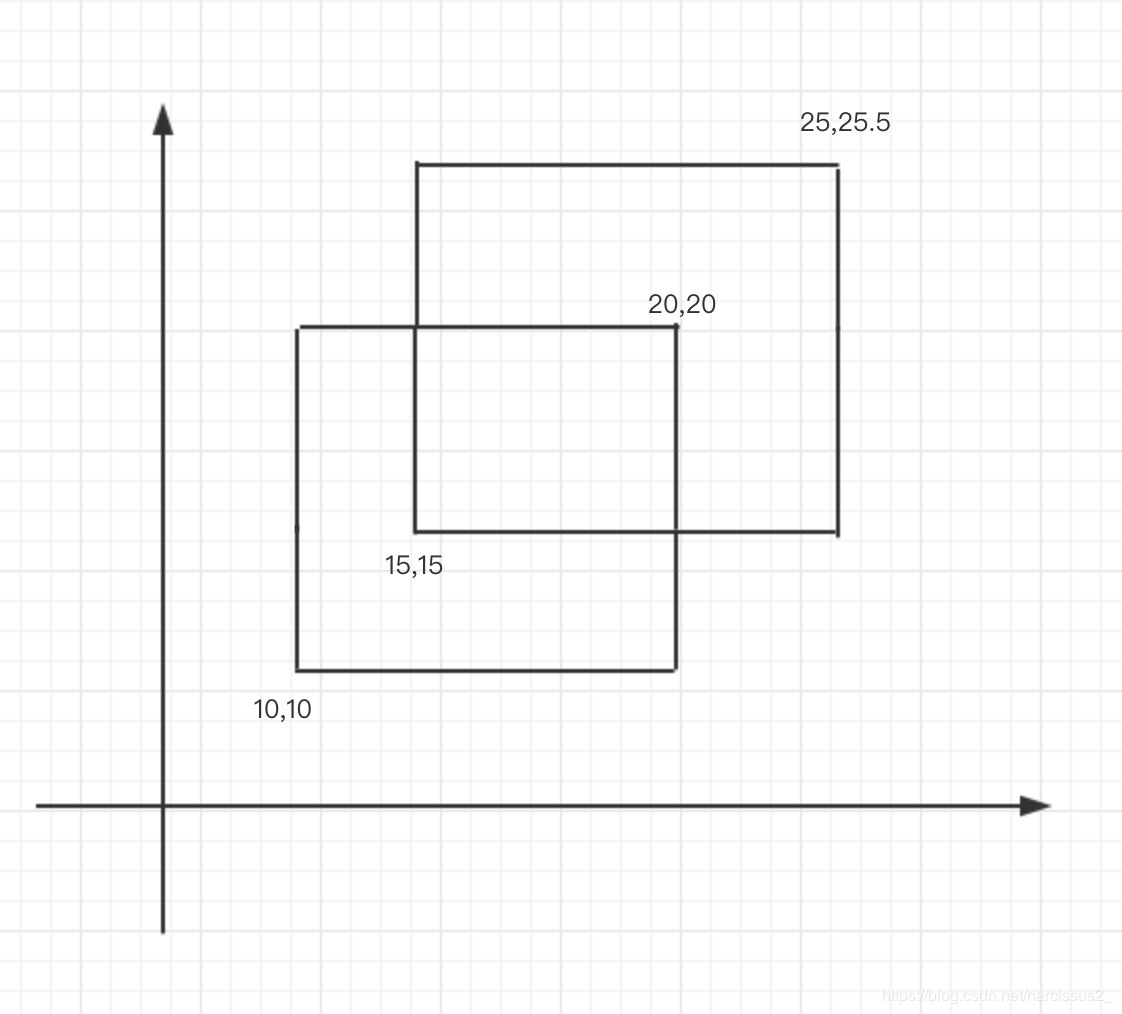
用矩形和减去矩形交集:
(20−10)∗(20−10)+(25−15)∗(25.5−15)−(20−15)∗(20−15)=180.0(20−10)∗(20−10)+(25−15)∗(25.5−15)−(20−15)∗(20−15)=180.0
这样算非常的耗费时间,因为每个矩形都需要两两配对,查看互相之间是否有交集。
优化方法
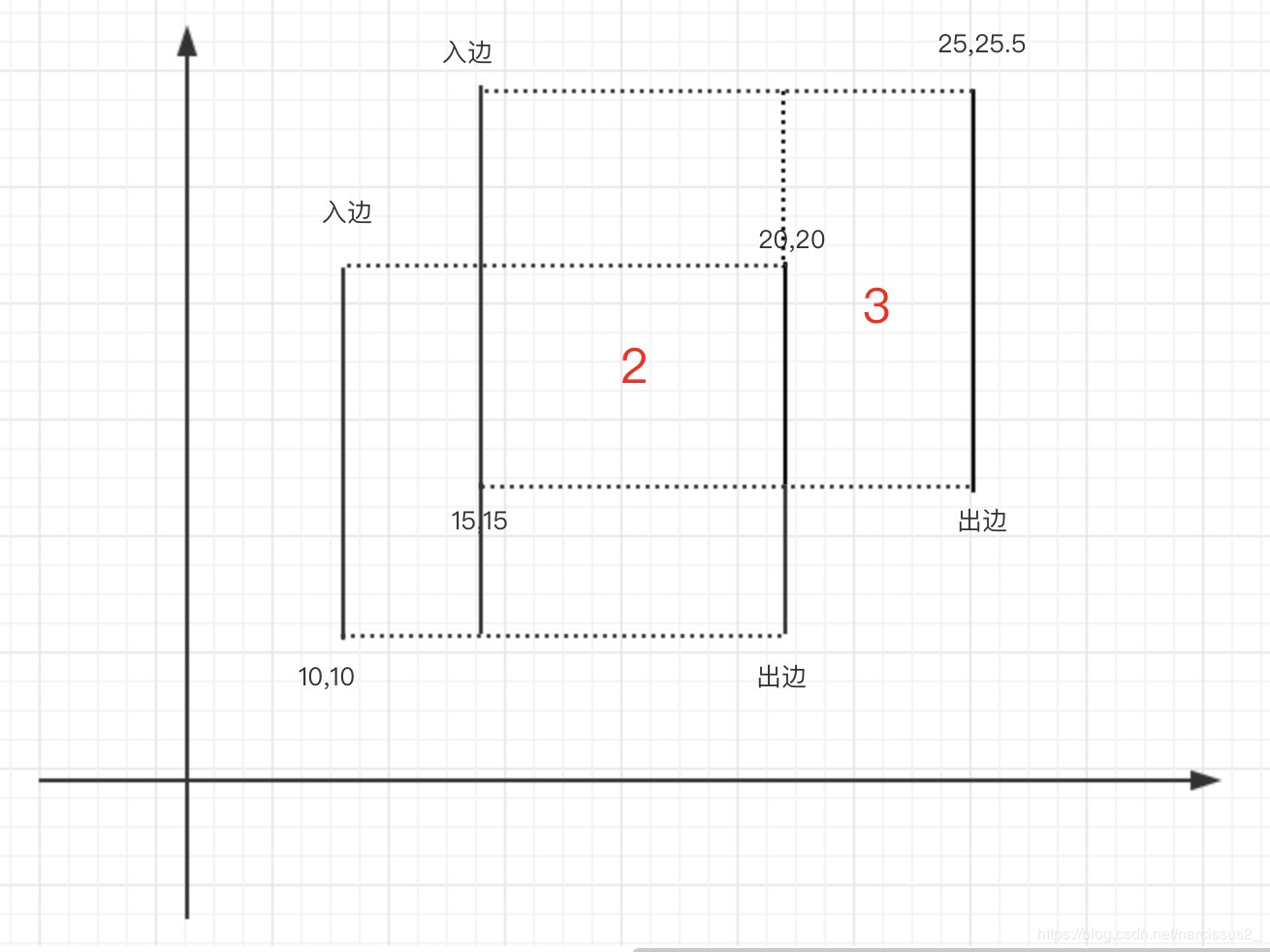
把这两个矩形分成三个
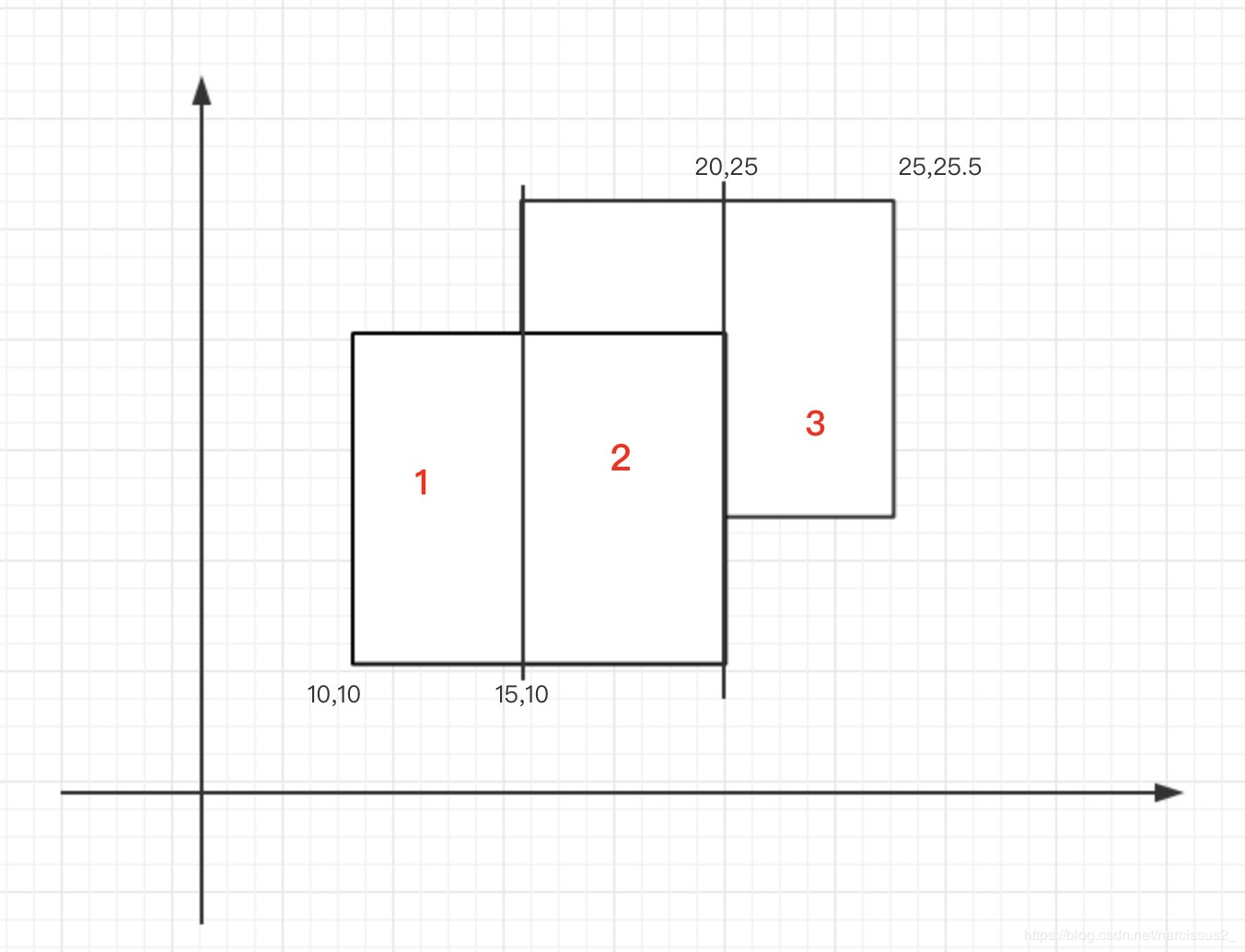
于是现在就变成了(20−10)∗(15−10)+(25.5−10)∗(20−15)+(25.5−15)∗(25−20)=180(20−10)∗(15−10)+(25.5−10)∗(20−15)+(25.5−15)∗(25−20)=180
采取这个方法的好处: 只需要从左往右扫,一步一更新即可
那这种方法需要有哪些信息呢?
- 每个新矩形的的高度。
- 每个新矩形的宽度。
那我们先从计算宽度说起
1.其实计算宽度特简单。我们把垂直于x的边单独挑出来。
然后按照x的大小排个序,隔位相减就可以得到。如width[0]=15−10;width[1]=20−15;....
那现在来计算矩形的高度,矩形高度怎么计算呢?这是整个扫描线最难理解的地方。
定义:在同一个矩形内,从左往右看,第一条看到的边为“入边”,第二条看到的边为“出边”
其实所谓的从左往右(也可以是从上往下),就是扫描线的方向。
当从左往右扫,遇到入边的线,则对入边区间扫到进行+1操作,遇到出边,那么对出边区间进行-1操作
步骤
(出入边赋值已完成)
1.第一条为入边,区间为[10,20],则区间[10,20] +1(此时区间[10,20] = 1)
2.查看整个区间,只有[10,20]有值,则width[0]10 = 50
3.第二条边为入边,区间为[15,25.5],则[15,25.5]+1(此时区间[10,15]=1,[15,20]=2,[20,25.5]=1)
4.查看整个域区间,从[10,25.5]有值,则width[1](25.5-10) = 77.5
5.第三条边为出边,区间从[10,20],则[10,20]-1(此时区间为[15,25.5] = 1)
6.查看整个区间,从[15,25.5]有值,则width[2]*(25.5-15) = 52.5
7.第四条边为出边,区间从[15,25.5],此时-1,整个区间没掉
8.整个区间没值,遍历结束。
将上述的区间模型转化成线段树(区间修改+区间查询)
问题1,离散化
先说离散化,这里面牵扯到小数,而线段树是维护一个整数区间,这是我们首先遇到的问题
(1)把y坐标离散化
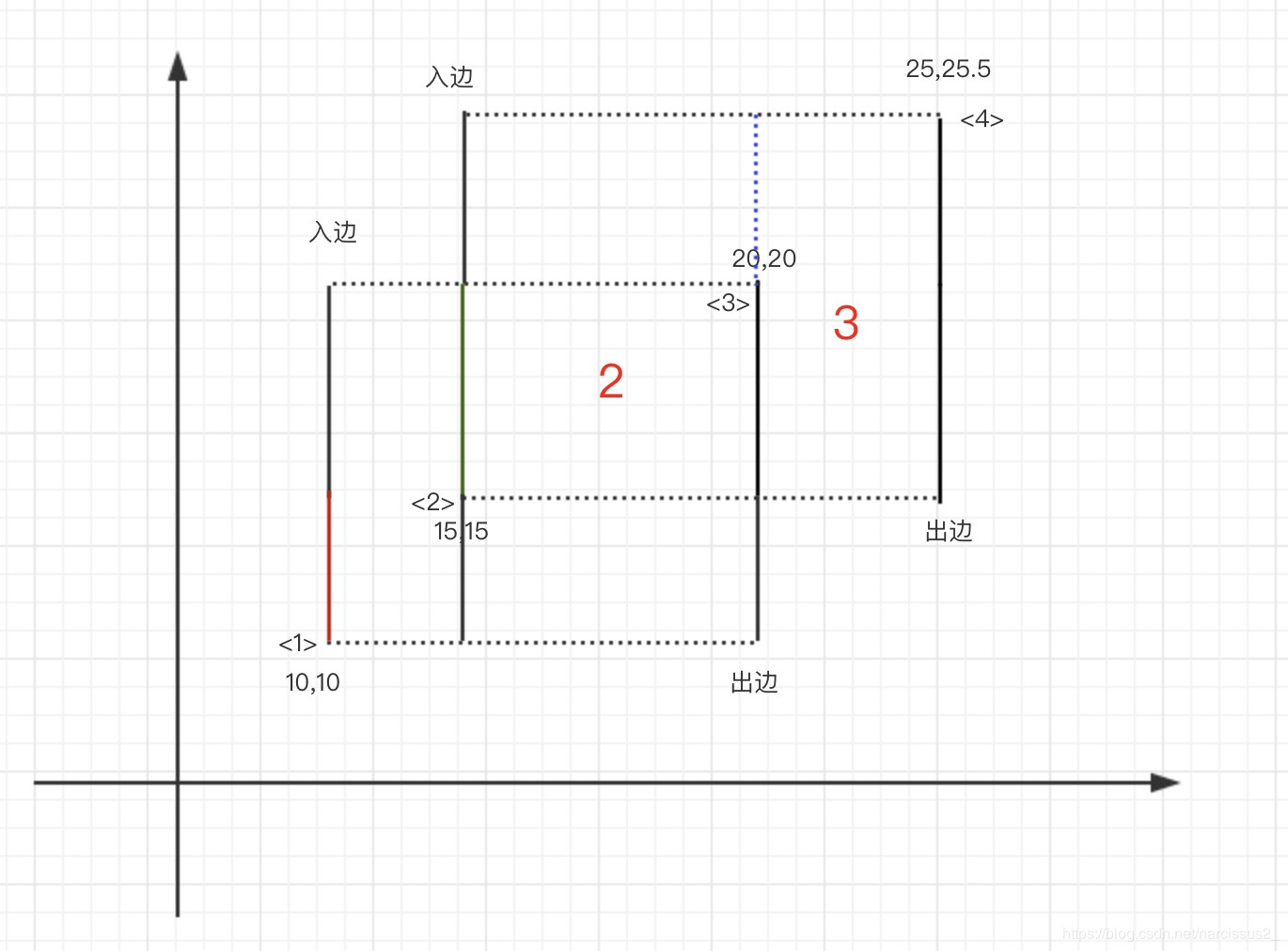
(2)用一个区间数组记录每个区间的值:于是现在[10,15]成为块1,[15,20]成为块2,[20,25.5]成为块3。
(3)则现在更新第一条入边[10,20]就变成更新[1,3],更新第二条边就变成更新[2,4],之后再查表全部乘起来即可
问题2:怎么维护区间信息,使得调用query()就可以返回总共存在值的区间长度?
这个和染色问题是一样的,用一个cover表示区间[left,right]被覆盖的次数,用len表示这个区间的合法长度,那query(1到n)的合法长度,自然就能返回 总共的区间长度了。
解题步骤
建树
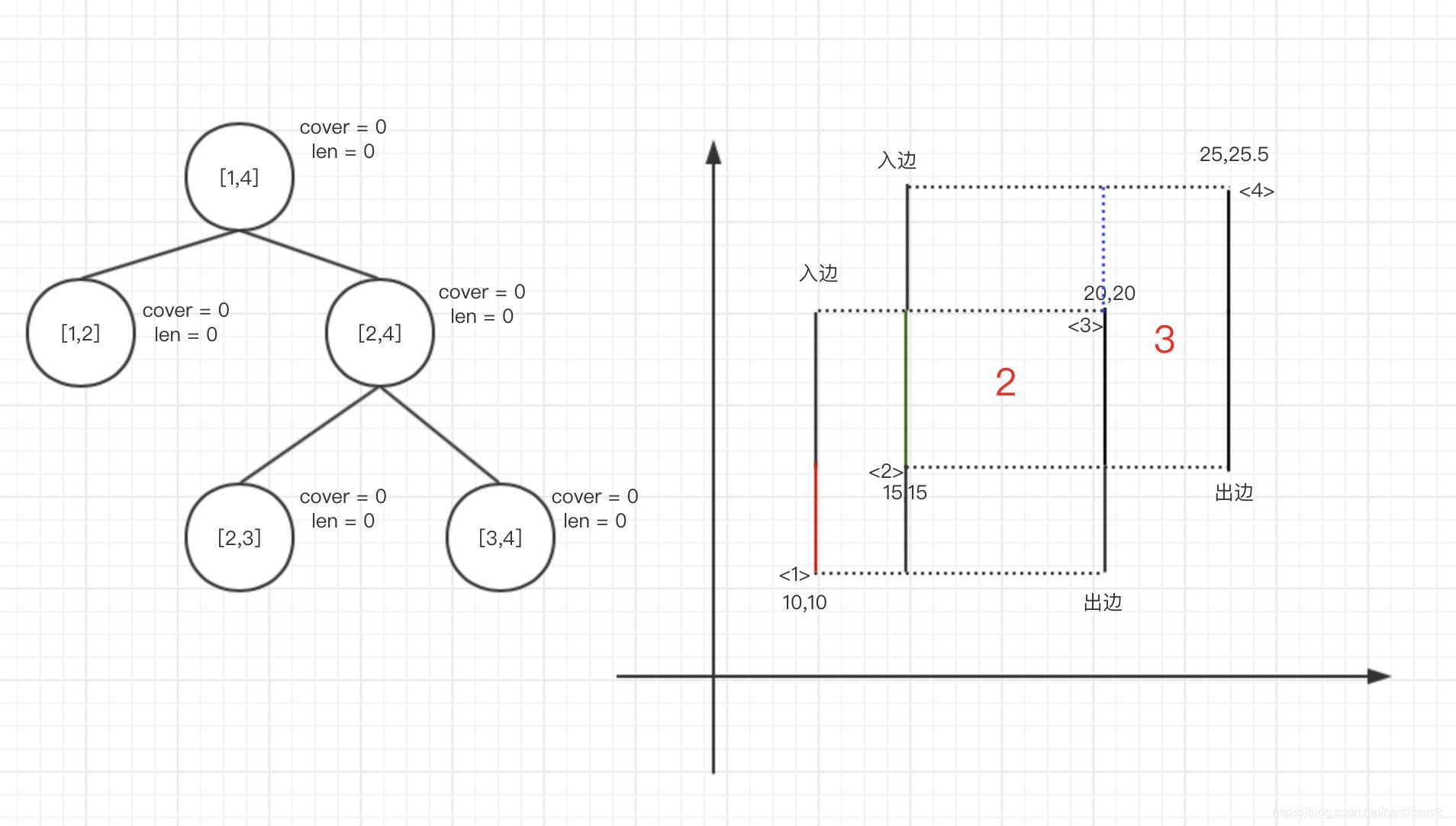
仔细观察,这棵树似乎和之前的线段树不一样,它的叶子节点的[l,r]不相等,而是差别为1,。
这是因为点对于求面积的题目毫无意义,我们最需要的是它每一个基础的“块”。
1.第一条为入边,区间为[1,3],则区间cover[1,3] +1(此时区间[1,3] = 1)
2.query整个域的区间,得到len=10,则width[0] * 10 = 50
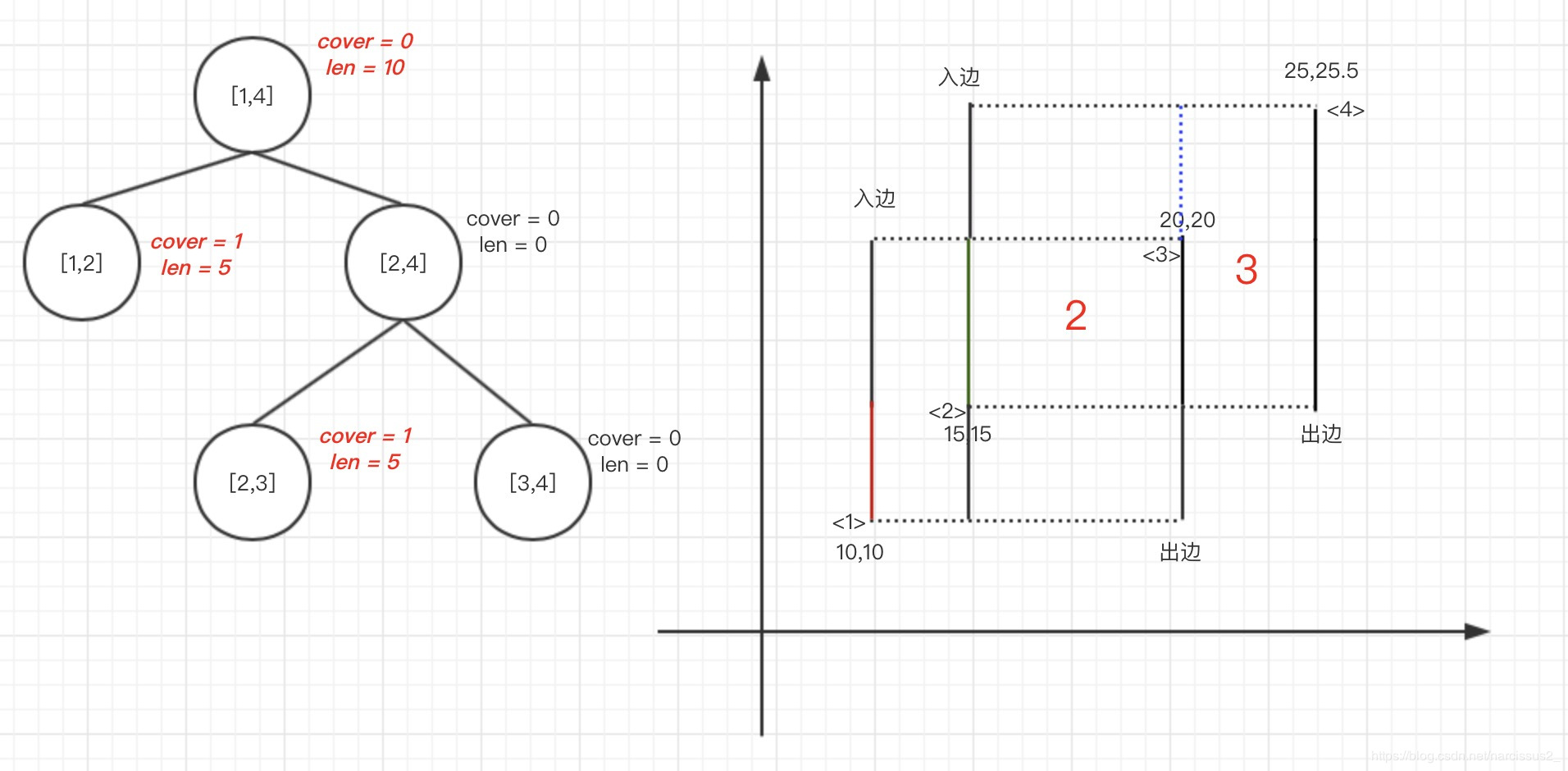
3.第二条边为入边,区间为[2,4],则cover[2,4]+1(此时如图所示)
4.query整个区间,得到len = 15.5,则width[1] * (25.5-10) = 77.5
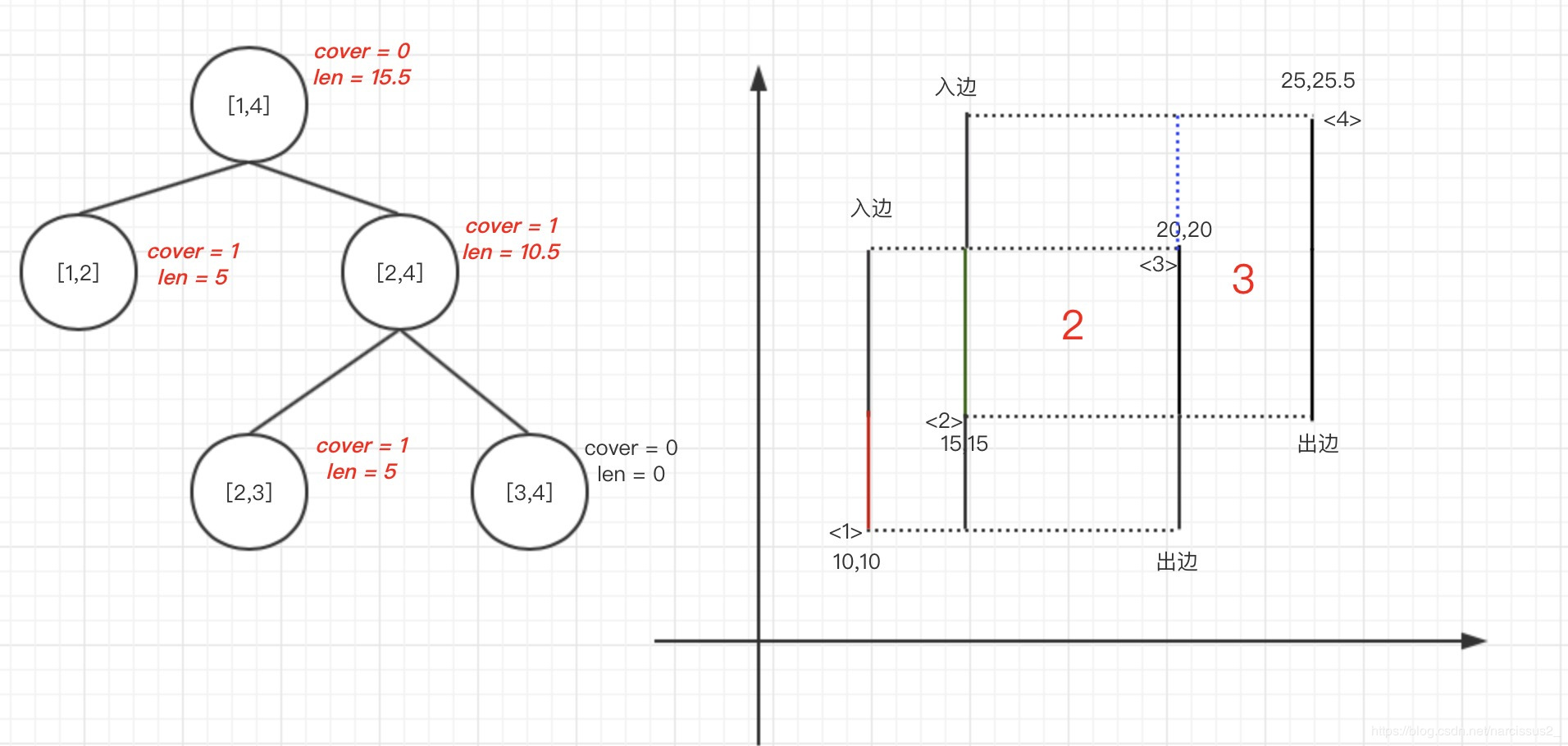
6.第三条边为出边,区间从[1,3],则[1,3]-1
7.query整个区间,得到10.5,则width[2] * 10.5 = 52.5
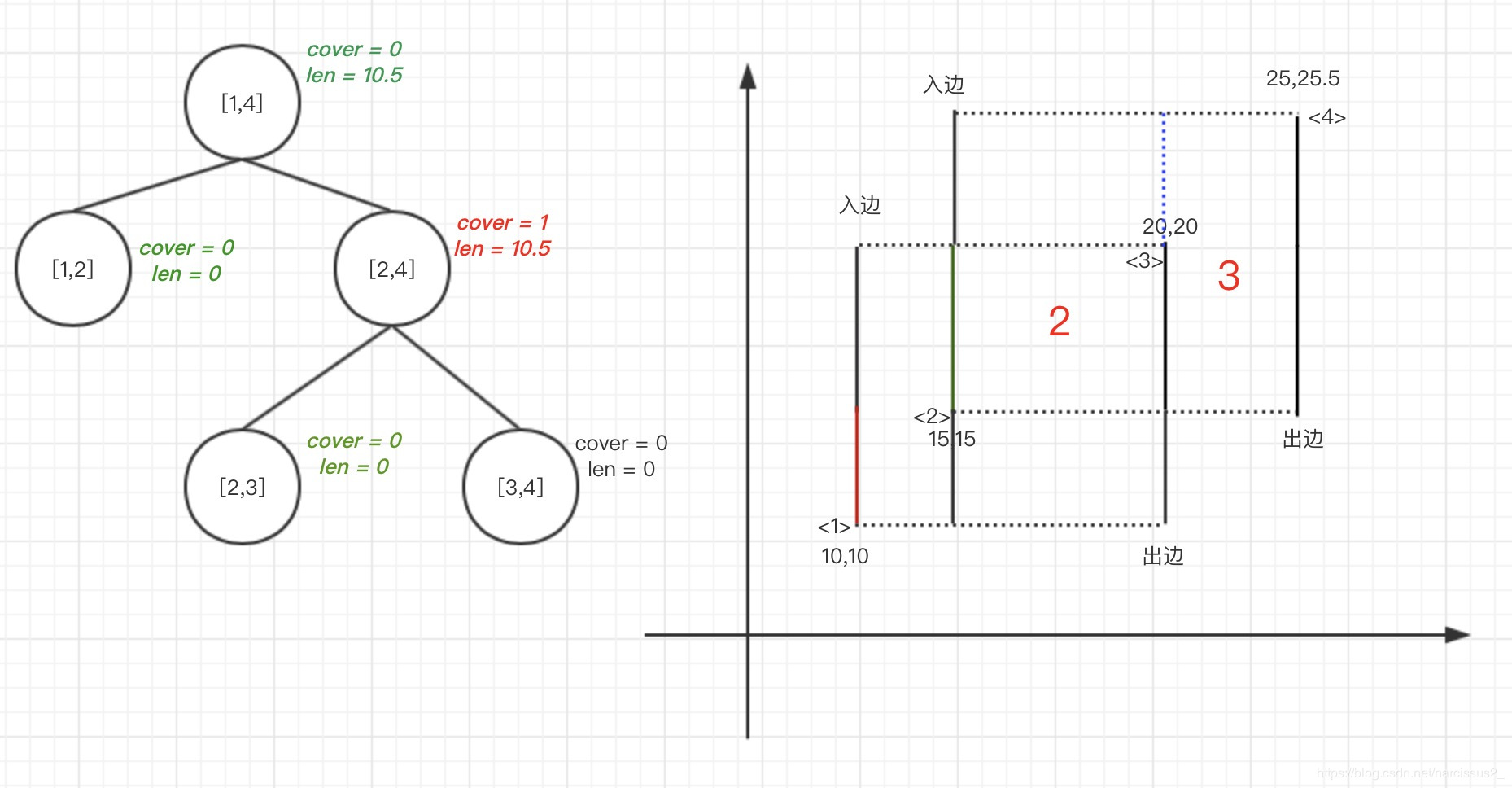
7.第四条边为出边,区间从[15,25.5],此时-1,整个区间没掉
8.query整个区间,值为0,遍历结束。
#include<iostream>
#include<algorithm>
#include<cstring>
#include<vector>
using namespace std;
#define lc u<<1
#define rc u<<1|1
const int N=10010;
struct Line
{
double x,y1,y2;
int k;
bool operator<(const Line &W) const
{
return x<W.x;
}
}line[N<<1];
struct Node
{
int l,r;
int cnt;
double len;
}tr[N<<3];
double ys[N<<1];
int n;
int cnt;
void pushup(int u)
{
if(tr[u].cnt)//若cnt>0,则为区间长度
tr[u].len=ys[tr[u].r]-ys[tr[u].l];
else if(tr[u].l + 1 == tr[u].r)//cnt=0,且为叶子结点,则当前区间长度为0
tr[u].len=0;
else //cnt=0,且不为叶子结点,用子节点更新父节点,
tr[u].len=tr[lc].len+tr[rc].len;
}
void build(int u,int l,int r)
{
tr[u]={l,r};
if(l+1 == r)
return;
int mid=l+r>>1;
build(lc,l,mid);
build(rc,mid,r);
}
void print(int u)
{
if(tr[u].l)
{
cout<<u<<' '<<tr[u].l<<' '<<tr[u].r<<endl;
print(lc);
print(rc);
}
}
void modify(int u,int l,int r,int v)
{
if(l <= tr[u].l && tr[u].r <= r)
{
tr[u].cnt+=v;
pushup(u);
return;
}
// if(tr[u].l + 1 == tr[u].r)//如果更新条件取等号要特判叶子结点
// return;
int mid=tr[u].l+tr[u].r>>1;
if(l < mid)
modify(lc,l,r,v);
if(r > mid)
modify(rc,l,r,v);
pushup(u);
}
int main()
{
int kase=1;
while(scanf("%d",&n) && n)
{
cnt=0;
for(int i=1;i<=n;i++)
{
double x1,x2,y1,y2;
scanf("%lf%lf%lf%lf",&x1,&y1,&x2,&y2);
line[++cnt]={x1,y1,y2,1};
ys[cnt]=y1;
line[++cnt]={x2,y1,y2,-1};
ys[cnt]=y2;
}
sort(ys+1,ys+cnt+1);
sort(line+1,line+cnt+1);
int len=unique(ys+1,ys+cnt+1)-(ys+1);
build(1,1,len);
//print(1);
double res=0;
for(int i=1;i<=n*2;i++)
{
res+=tr[1].len*(line[i].x-line[i-1].x);
int y1=lower_bound(ys+1,ys+len+1,line[i].y1)-ys;
int y2=lower_bound(ys+1,ys+len+1,line[i].y2)-ys;
int k=line[i].k;
modify(1,y1,y2,k);
}
printf("Test case #%d\n", kase++);
printf("Total explored area: %.2f\n\n", res);
}
}
思想有点像打lazy标记,这里如果询问到整个区间[l,r],那么就直接在代表这个区间的点上面cnt+1。。。
要保证的是每个点的len值都是正确的。(len表示这段区间的覆盖长度)
pushup的话,就是 若cnt>0 len就是区间长度,否则是孩子区间长度的和。(保证每个点的len都是对的,那么要回溯pushup)
还有就是这棵线段树表示连续区间,所以是[l,mid][mid,r]而不是[l,mid][mid+1,r]..
把每个节点看成是一条线段。
对于每个节点维护两个值:
cnt:这个点所代表的线段被覆盖了多少次。
len:以这个点为根的子树中被覆盖的区间一共有多长。
当一条线段进来的时候,在代表它的那若干个节点上cnt++,其它节点cnt不用加。
然后len维护的就是这个区间内那些cnt>0的节点所覆盖的区间总长。
做惯了叶子节点才有实际意义的线段树,思路太过狭隘,被卡了这么久,其实线段树上每个节点都可以有它的实际意义。
hdu1828
说完了矩形面积,矩形周长的方法自然是类似的,但是周长的计算却更复杂些
周长可以分成两部分计算,横线和竖线,如图将所有彩色的横线加起来就是横向的所有长度了
然后可以采用竖直方向的扫描线将竖线的所有长度求出来
那么怎么计算横线的长度呢?
横线的长度 = abs(现在这次修改后总区间被覆盖的长度和修改前区间总长度之差)下边–插入,上边–删除
acwing1277
题目要求有三种操作,两种是不同的在线修改,还有一种是在查询取模后的结果。而这两种操作又是区间乘法和区间.
面对这两种操作,可以联想到线段树的一个非常好的功能就是lazytag,只计算出确实需要访问的区间的真实值,其他的保存在lazytag里面,这样可以近似O(NlogN)的运行起来。在尝试着写了只有一个lazetag的程序之后我们发现一个lazytag是不能够解决问题的,那就上两个,分别表示乘法意义上的lazytag和加法意义上的lazytag。紧接着想到pushdown操作之后我们又发现必须在向下传递lazytag的时候人为地为这两个lazytag规定一个先后顺序,排列组合一下只有两种情况:
①加法优先,即规定好segtree[root2].value=((segtree[root2].value+segtree[root].add)*segtree[root].mul)%p,问题是这样的话非常不容易进行更新操作,假如改变一下add的数值,mul也要联动变成奇奇怪怪的分数小数损失精度;
②乘法优先,即规定好segtree[root2].value=(segtree[root2].valuesegtree[root].mul+segtree[root].add(本区间长度))%p,这样的话假如改变add的数值就只改变add,改变mul的时候把add也对应的乘一下就可以了,没有精度损失,看起来很不错。



#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
typedef long long LL;
const int N = 100010;
int n, p, m;
int w[N];
struct Node
{
int l, r;
int sum, add, mul;
}tr[N * 4];
void pushup(int u)
{
tr[u].sum = (tr[u << 1].sum + tr[u << 1 | 1].sum) % p;
}
void eval(Node &t, int mul, int add)
{
t.sum = ((LL)t.sum * mul + (LL)(t.r - t.l + 1) * add) % p;
t.mul = (LL)t.mul * mul % p;
t.add = ((LL)t.add * mul + add) % p;
}
void pushdown(int u)
{
eval(tr[u << 1], tr[u].mul, tr[u].add);
eval(tr[u << 1 | 1], tr[u].mul, tr[u].add);
tr[u].add = 0, tr[u].mul = 1;
}
void build(int u, int l, int r)
{
if (l == r) tr[u] = {l, r, w[r], 0, 1};
else
{
tr[u] = {l, r, 0, 0, 1};
int mid = l + r >> 1;
build(u << 1, l, mid), build(u << 1 | 1, mid + 1, r);
pushup(u);
}
}
void modify(int u, int l, int r, int mul, int add)
{
if (tr[u].l >= l && tr[u].r <= r) eval(tr[u], mul, add);
else
{
pushdown(u);
int mid = tr[u].l + tr[u].r >> 1;
if (l <= mid) modify(u << 1, l, r, mul, add);
if (r > mid) modify(u << 1 | 1, l, r, mul, add);
pushup(u);
}
}
int query(int u, int l, int r)
{
if (tr[u].l >= l && tr[u].r <= r) return tr[u].sum;
pushdown(u);
int mid = tr[u].l + tr[u].r >> 1;
int sum = 0;
if (l <= mid) sum = query(u << 1, l, r);
if (r > mid) sum = (sum + query(u << 1 | 1, l, r)) % p;
return sum;
}
int main()
{
scanf("%d%d", &n, &p);
for (int i = 1; i <= n; i ++ ) scanf("%d", &w[i]);
build(1, 1, n);
scanf("%d", &m);
while (m -- )
{
int t, l, r, d;
scanf("%d%d%d", &t, &l, &r);
if (t == 1)
{
scanf("%d", &d);
modify(1, l, r, d ,0);
}
else if (t == 2)
{
scanf("%d", &d);
modify(1, l, r, 1 ,d);
}
else printf("%d\n", query(1, l, r));
}
return 0;
}












tql!