最短路三大算法:
bfs(O(n + m)), dijkstra(O(mlogn)), spfa(O(m)), 双端队列bfs(O(n))
写在前面
n为点数 m为边数
邻接表涉及的数组大小全部开为M(边数) * 2(因为可能会爆掉)
啊哈算法有详解
1.
稠密图(m ~ n^2) -> 朴素dijkstra o(n^2); < 堆优化dijkstra o(n^2logn) -> 邻接数组存储
稀疏图(m ~ n) -> 堆优化dijkstra o(mlogn) -> 邻接表存储
2.
对经过的边数进行限制
1) 最多经过k条边的最短路:不能用SPFA, 只能用bellman-ford算法
2) 恰好经过k条边, 边可重复经过的最短路:bellmon-ford变形 / 倍增 + floyd变形 牛站
3.
有向图和无向图的最短路都是一样的解决方法(无向图是特殊的有向图)
4.
自环一定不会出现在最短路的路径中
重边里只用存最短的一条边
5.dijkstra 如果当一个点被拿出堆之后, 还能被其他点更新, dijkstra就不能用
因为dijkstra是基于贪心的一种算法, 如果局部最优不能使得整体最优的话, 也就是当前最优, 不是最后的最优解, 那么该算法则不能适用
而对于这种问题bellmon-ford和spfa算法则可以, 因为算法本来就不是用当前最优来代替最优解的, 而是通过不断的更新当最后的解才是最优解, 基于dp的一种思想, 解会不断被更新. 所以spfa算法的应用范围会相对来说广.
算法思想: 迭代一次的话, 求出边数为1的路径的花费最小值, 迭代2次, 求出边数为二的路径的花费最小值, 迭代n-1次求出所有边数为n-1的路径的花费最小值, 由于是求最短路径, 正环越走越多, 负环越走越少-∞, 所以都不需要考虑, 对于n个顶点的图, 无环路径边数最多为n-1条
6.spfa与dijkstra对比
spfa的应用比dijkstra广很多, 但是spfa容易被卡常数, O(km)的k, 而dijkstra的复杂度铁定mlogn
spfa很多问题都能用但不是很多问题都能快
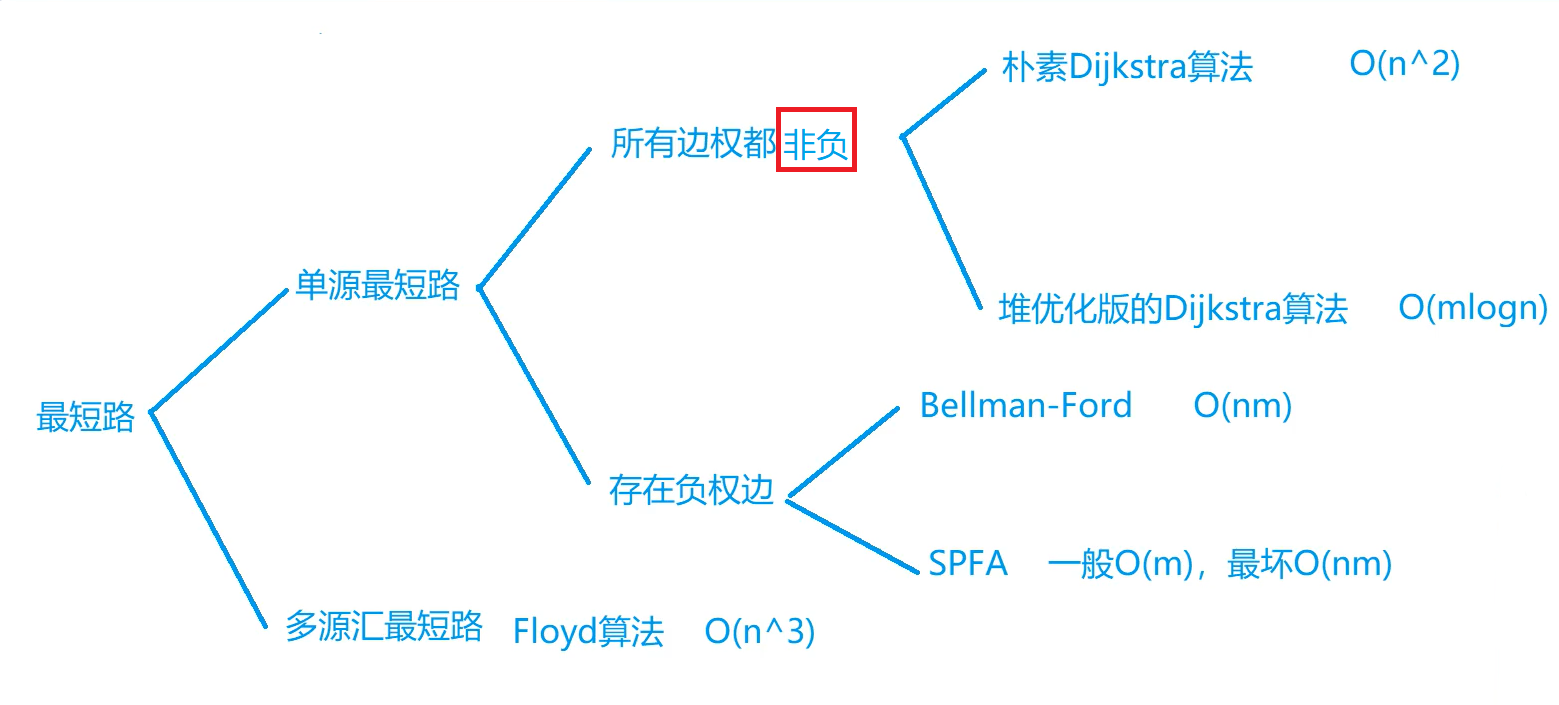
更正: SPFA 算法的时间复杂度是 O(km),其中 k 一般情况下是个很小的常数,最坏情况下是 n

