DFS
emmm…感谢 y总 和 lyd 大佬
深度优先遍历(DFS),就是在每个点 x 上面对多条分支时,任意选一条边走下去,执行递归,直至回溯到点 x 后,再考虑走向其他的边
void dfs(int x){
v[x] = 1; // 记录点 x 被访问过
for(int i = h[x]; ~i; i = ne[i]){
int y = e[i];
if(v[y]) continue;
dfs(y);
}
}
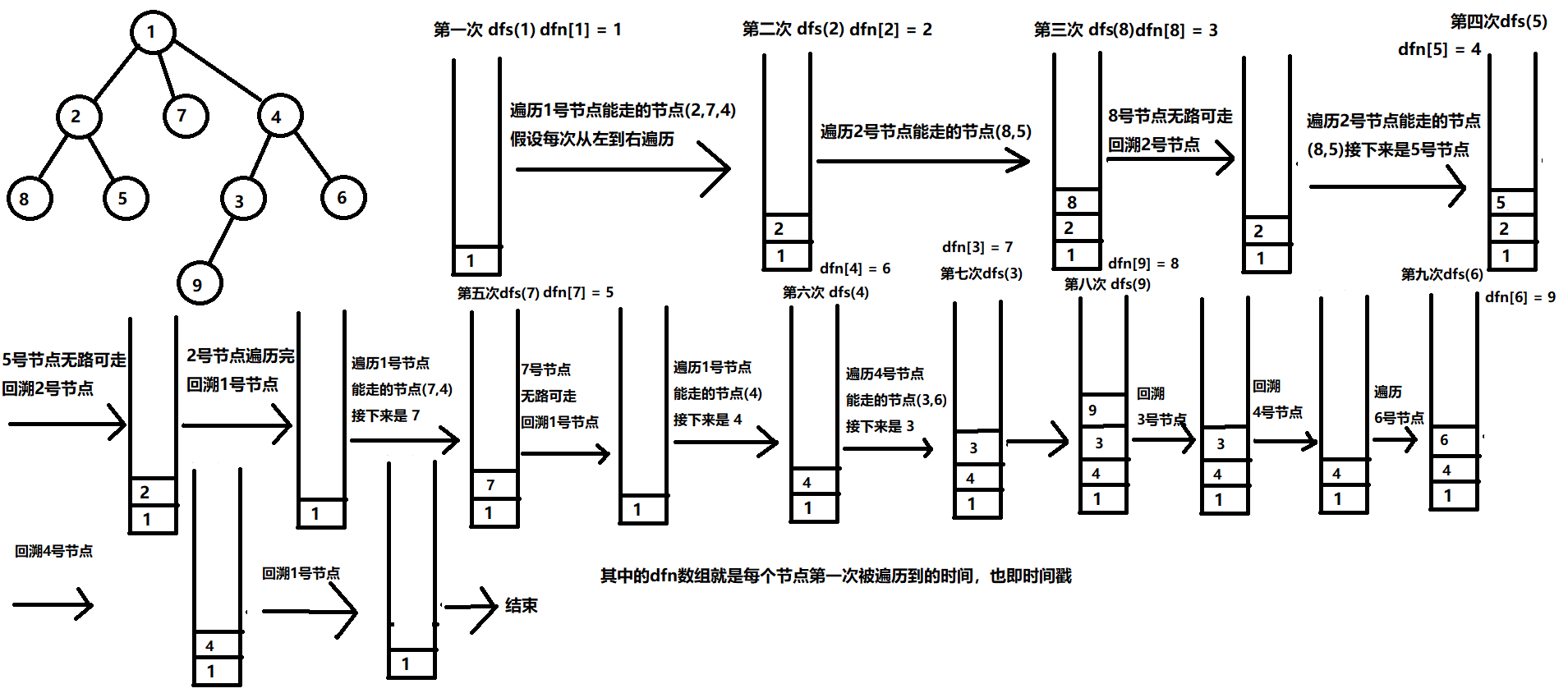
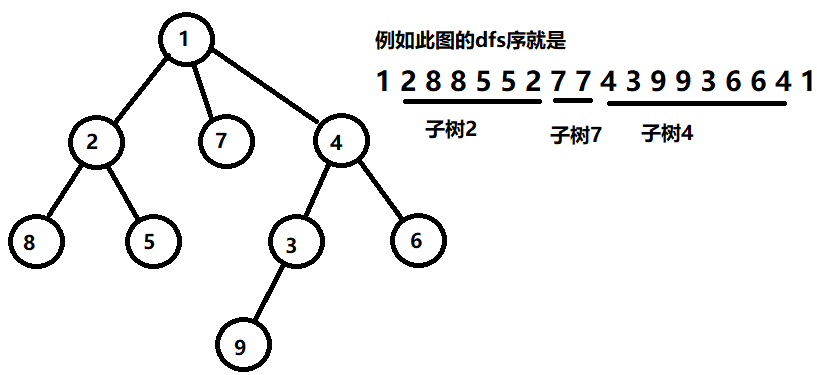
树的dfs序
我们在对树进行深度优先遍历时,对于每个节点,在刚进入递归后以及即将回溯前各记录一次该点的编号,最后产生长度为 2 * n 的节点序列称为 dfs 序
void dfs(int x){
a[ ++ m] = x;
v[x] = 1; // 记录点 x 被访问过
for(int i = h[x]; ~i; i = ne[i]){
int y = e[i];
if(v[y]) continue;
dfs(y);
}
a[ ++ m] = x;
}
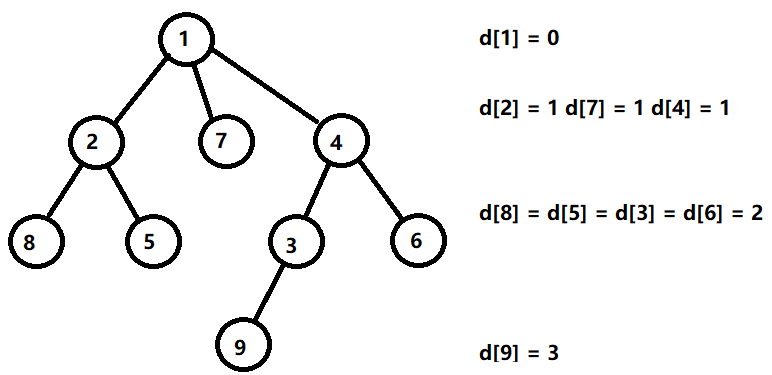
树的深度
void dfs(int x){
v[x] = 1; // 记录点 x 被访问过
for(int i = h[x]; ~i; i = ne[i]){
int y = e[i];
if(v[y]) continue;
d[y] = d[x] + 1;
dfs(y);
}
}
图的连通块划分
上面的代码每从 x 开始一次遍历,就会访问 x 能够到达的所有的点与边。因此通过多次深度优先遍历,可以划分出一张无向图中的各个连通块(若在无向图的一个子图中,任意两个节点之间都存在一条路径(可以互相到达),并且这个子图是”极大”的(不能再扩张),则称该子图为无向图的一个连通块。一张不连通的无向图由2个或2个以上连通块组成,而一张无向连通图整体是一个连通块)
void dfs(int x){
v[x] = cnt; // 记录点 x 被访问过
for(int i = h[x]; ~i; i = ne[i]){
int y = e[i];
if(v[y]) continue;
dfs(y);
}
}
for(int i = 1; i <= n; i ++)
if(!v[i]){
cnt ++;
dfs(i);
}
DFS 之连通性模型
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 110;
char g[N][N];
int n, T, sx, sy, ex, ey;
bool st[N][N];
int dx[] = {-1, 0, 1, 0}, dy[] = {0, 1, 0, -1};
bool dfs(int x, int y)
{
if(g[x][y] == '#') return false;// 当前路不能走
if(x == ex && y == ey) return true;// 走到终点
st[x][y] = 1;// 标记当前已经走过
for(int i = 0; i < 4; i ++){
int nx = x + dx[i], ny = y + dy[i];
if(nx < 0 || nx >= n || ny < 0 || ny >= n) continue; // 超出边界
if(st[nx][ny]) continue;// 已经被走过
if(dfs(nx, ny)) return true;
}
return false;
}
int main()
{
cin >> T;
while(T -- ){
cin >> n;
for(int i = 0; i < n; i ++) cin >> g[i];
memset(st, 0, sizeof st);
cin >> sx >> sy >> ex >> ey;
if(dfs(sx, sy)) puts("YES");
else puts("NO");
}
return 0;
}
这个题目就是进行有效(排除路不能走、已经被走过、超出边界 3 种情况下)的 dfs 的次数
#include<iostream>
#include<cstring>
#include<cstdio>
#include<algorithm>
using namespace std;
const int N = 25;
char g[N][N];
bool st[N][N];
int n, m;
int dx[] = {0, -1, 0, 1}, dy[] = {1, 0, -1, 0};
int res;
void dfs(int x, int y)
{
res ++ ;
st[x][y] = 1;
for(int i = 0; i < 4; i ++){
int nx = x + dx[i], ny = y + dy[i];
if(nx < 0 || nx >= n || ny < 0 || ny >= m) continue;
if(g[nx][ny] != '.') continue;
if(st[nx][ny]) continue;
dfs(nx, ny);
}
}
int main()
{
while(cin >> m >> n , n || m){
for(int i = 0; i < n; i ++) cin >> g[i];
int x, y;
for(int i = 0; i < n; i ++)
for(int j = 0; j < m; j ++)
if(g[i][j] == '@'){
x = i;
y = j;
}
res = 0;
memset(st, 0, sizeof st);
dfs(x, y);
cout << res << endl;
}
return 0;
}
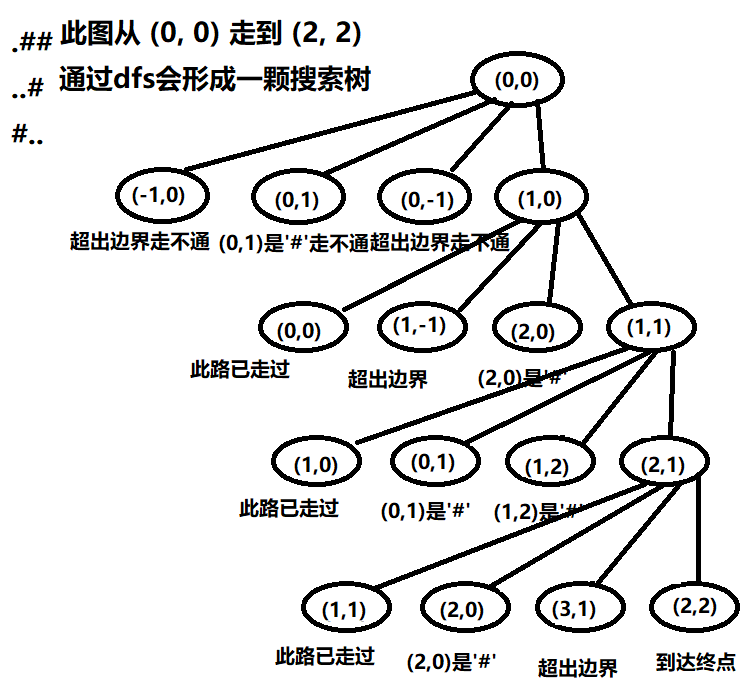
DFS之搜索顺序
这里我们就可以将”问题空间”类比为一张图,其中的状态类比为节点,状态之间的联系与可达性就用图中的边来表示,那么使用深度优先搜索算法求解问题,就相当于在一张图上进行深度优先遍历。
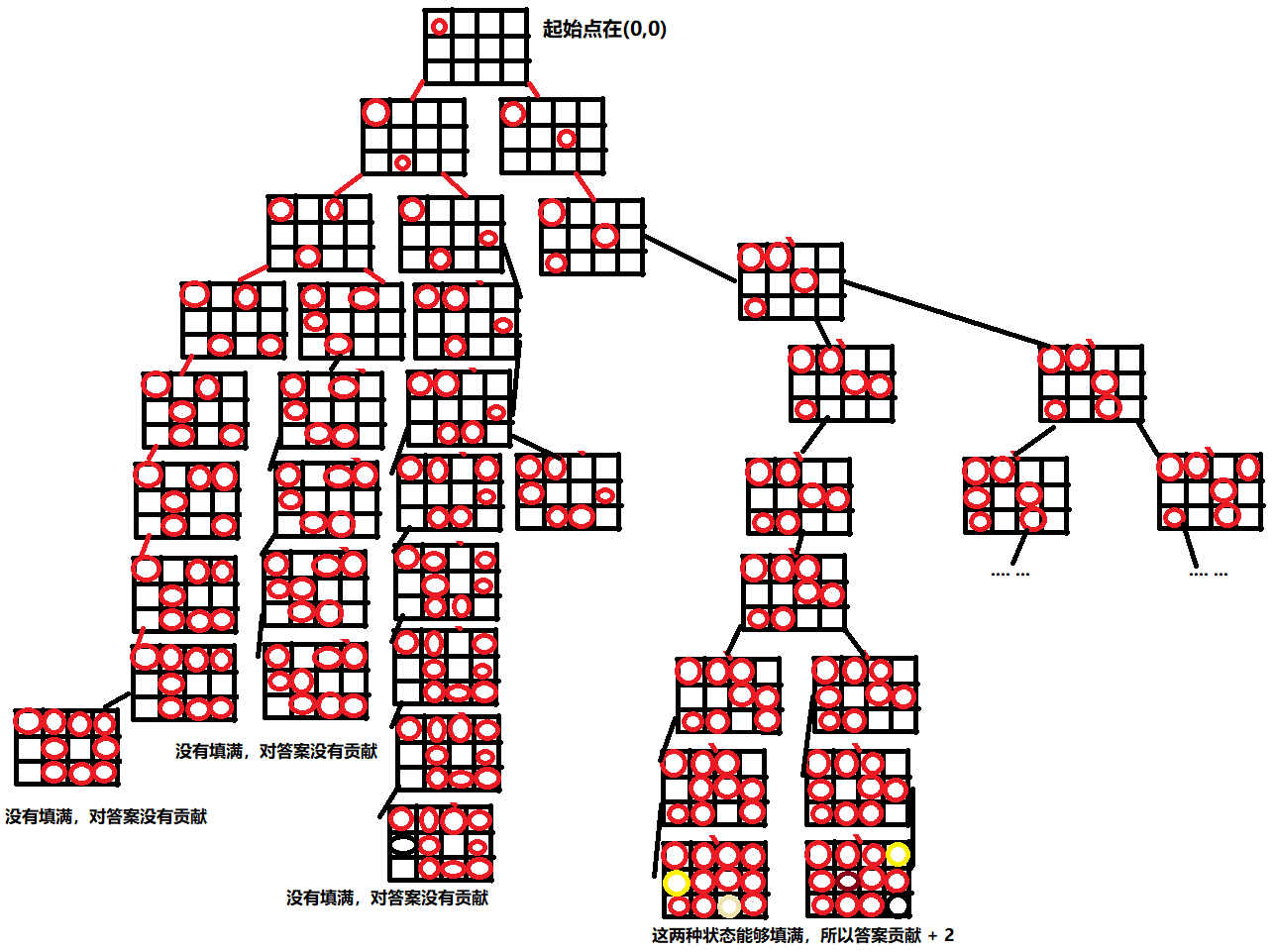
将棋盘中棋子的各个位置摆放看成是一个状态,状态之间的可达性由棋子的下一次跳动决定。然后需要注意的就是在回溯的时候需要注意复原上一个节点的状态。
搜索边界当前没有可以跳的位置
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 15;
bool st[N][N];
int res, n, m, sx, sy, T;
int dx[] = {-2, -1, 1, 2, 2, 1, -1, -2};
int dy[] = {-1, -2, -2, -1, 1, 2, 2, 1};
void dfs(int x, int y, int cnt)
{
if(cnt == n * m){
res ++;
return ;
}
st[x][y] = 1; // 标记当前点已被走过
for(int i = 0; i < 8; i ++){
int nx = x + dx[i], ny = y + dy[i];
if(nx < 0 || nx >= n || ny < 0 || ny >= m) continue; // 超出边界
if(st[nx][ny]) continue; // 当前状态的当前点被走过
dfs(nx, ny, cnt + 1);
}
st[x][y] = 0; // 恢复上一次的棋盘状态,就是将当前点的标记去了也即恢复之前的状态
}
int main()
{
cin >> T;
while(T --){
cin >> n >> m >> sx >> sy;
res = 0;
dfs(sx, sy, 1);
cout << res << endl;
}
return 0;
}
emmm…这个题目可以将每个单词看成是一个状态,状态之间的可达性由单词能否进行合并决定
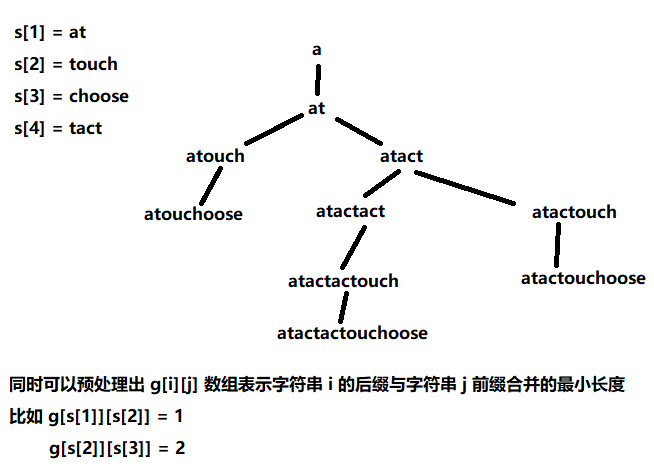
搜索边界 当前没有可选择的单词
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 25;
int g[N][N], ans, n, st[N];
string str[N];
char sta;
void dfs(string res, int now)
{
ans = max((int)res.size(), ans);
st[now] ++;// 表示该单词已被使用一次
for(int i = 0; i < n; i ++){// 遍历所有单词,如果当前单词可用就合并当前单词
if(st[i] < 2 && g[now][i]){
dfs(res + str[i].substr(g[now][i]), i);
}
}
st[now] --;// 恢复现场
}
int main()
{
cin >> n;
for(int i = 0; i < n; i ++) cin >> str[i];
cin >> sta;
for(int i = 0; i < n; i ++) // 预处理那些单词之间能够合并,并且需要合并的最少字母
for(int j = 0; j < n; j ++){
string a = str[i], b = str[j];
for(int k = 1; k < min(a.size(), b.size()); k ++)
if(a.substr(a.size() - k, k) == b.substr(0, k)){
g[i][j] = k;
break;
}
}
for(int i = 0; i < n; i ++)
if(str[i][0] == sta)
dfs(str[i], i);
cout << ans << endl;
return 0;
}
emmm…这个题目可以将许多的互质组合并起来看成一个状态,状态之间的联系由当前数字放在那个互质组决定。
递归到当前数字时,遍历所有的互质组检查能放在那一组
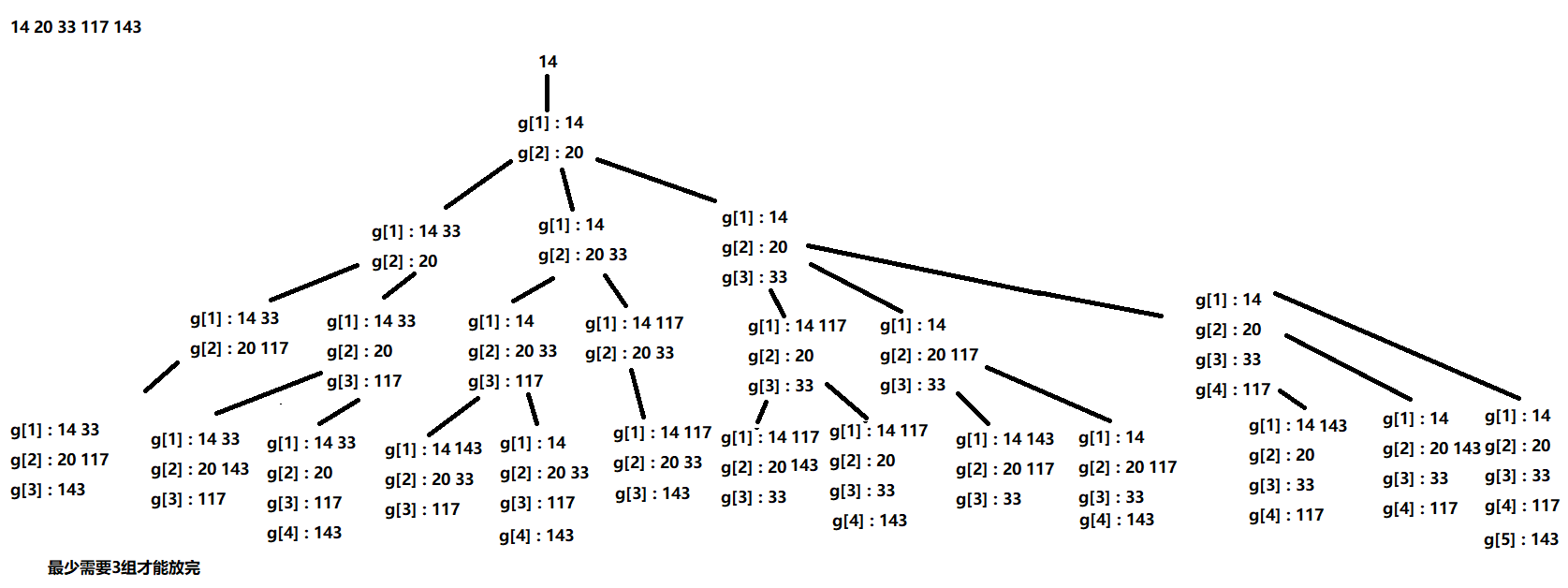
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<queue>
using namespace std;
const int N = 15;
vector < int > g[N];
int res, n, p[N], len;
int gcd(int a, int b)
{
return a == 0 ? b : gcd(b % a, a);
}
bool check(int x, int u)
{
for(int i = 0; i < g[x].size(); i ++)
if(gcd(p[g[x][i]], p[u]) > 1)
return false;
return true;
}
void dfs(int u)
{
if(len > res) return ;
if(u == n){// 遍历完所有数字,当前的组数和答案取一个最小值
res = min(res, len);
return ;
}
for(int i = 0; i < len; i ++){// 遍历每一组看是否能放当前数字
if(check(i, u)){
g[i].push_back(u);
dfs(u + 1);
g[i].pop_back();
}
}
g[len ++ ].push_back(u);
dfs(u + 1);
g[ -- len].pop_back();
}
int main()
{
cin >> n;
for(int i = 0; i < n; i ++) cin >> p[i];
res = n;
dfs(0);
cout << res << endl;
return 0;
}
DFS之剪枝与优化
剪枝 就是减小搜索树规模、尽早排除搜索树中不必要的分支的一种手段。形象地看,就好像剪掉了搜索树的枝条,故称为剪枝。
1、优化搜索顺序
在一些搜索问题中,搜索树的各个层次、各个分支之间的顺序不是固定的。不同的搜索顺序会产生不同的搜索树形态,其规模大小也相差甚远。
2、排除等效冗余
在搜索过程中,如果我们能够判定从搜索树的当前节点上沿着某几条不同分支到达的子树是等效的,那么只需要对其中的一条分支执行搜索。
3、可行性剪枝
在搜索过程中,及时对当前状态进行检查,如果发现分支已经无法到达递归边界,就执行回溯。(某些题目条件的范围限制是一个区间,此时可行性剪枝也被称为“上下界剪枝”。
4、最优性剪枝
在最优化问题的搜索过程中,如果当前花费的代价已经超过了当前搜到的最优解,那么无论采取多么优秀的策略到达递归边界,都不可能更新答案。此时可以停止对当前分支的搜索,执行回溯。
5、记忆化
可以记录每个状态的搜索结果,在重复遍历一个状态时直接检索并返回。(就好像我们对图进行深度优先遍历时,标记一个节点是否已经被访问过。
emmm…这个题目可以将所有的缆车合并看成一个状态,状态之间的转移可以看成由将小猫放在那辆缆车决定
搜索树如同 <分成互质组> 类似
剪枝1 : 优化搜索顺序,将小猫按照重量递减排序(先放重量大的可以相对较快搜索出最优解)
剪枝2:最优性剪枝 如果当前搜到的小猫组数已经大于当前搜到的最优解的时候就立即回溯
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 25;
int sum[N], n, a[N], k, res, m;
void dfs(int u)
{
if(k >= res) return ; // 最优性剪枝
if(u == n + 1){ // 递归完所有的小猫
res = k;
return ;
}
for(int i = 0; i < k; i ++) // 遍历当前的所有缆车
if(sum[i] + a[u] <= m){ // 如果能够放下当前小猫
sum[i] += a[u];
dfs(u + 1);
sum[i] -= a[u];
}
sum[k ++ ] = a[u]; // 新开一个缆车
dfs(u + 1);
sum[ -- k] = 0;
}
int main()
{
cin >> n >> m;
for(int i = 1; i <= n; i ++) cin >> a[i];
sort(a + 1, a + 1 + n); // 优化搜索顺序
reverse(a + 1, a + 1 + n);
res = n;
dfs(1);
cout << res << endl;
return 0;
}
剪枝1 :在每个状态下,从所有未填的位置里选择“能填的合法数字”最少的位置,考虑该位置上填什么数,作为搜索的分支,而不是任意找出1个位置。(个人理解是让高层次的树枝少一点)
1、对于每行、每列、每个九宫格,分别用一个 9 位二进制(全局整数变量)保存那些数字还可以填。
2、对于每个位置,把它所在行、列、九宫格的3个二进制数位与(&)运算,就可以得到该位置能填那些数,用 lowbit 运算就可以把能填的数字取出。
3、当一个位置填上某个数后,把该位置所在的行、列、九宫格记录的二进制数的对应位改为 0 ,即可更新当前状态;回溯时改回 1 即可还原现场。
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 9, M = 1 << N;
int ones[M], map[M];
int row[N], col[N], cell[3][3];
char str[100];
void draw(int x, int y, int t, bool flg)// 对每个空格填上数字,还是恢复现场
{
if(flg) str[x * N + y] = t + '1';
else str[x * N + y] = '.';
int v = 1 << t;
if(!flg) v = -v;// 是否加减,只需要一次取反就可以
row[x] -= v;
col[y] -= v;
cell[x / 3][y / 3] -= v;
}
bool dfs(int cnt)
{
if(!cnt) return true;// 找到正确答案就全部返回
int x, y, minv = 10;
for(int i = 0; i < N; i ++)// 每次找出每个空格中需要填的数字最少的空格
for(int j = 0; j < N; j ++)
if(str[i * N + j] == '.'){
int state = row[i] & col[j] & cell[i / 3][j / 3];
if(ones[state] < minv){
minv = ones[state];
x = i, y = j;
}
}
int state = row[x] & col[y] & cell[x / 3][y / 3];
for(int i = state; i > 0; i -= i & -i){// 枚举需要填的每个数字
int t = map[i & -i];
draw(x, y, t, 1);
if(dfs(cnt - 1)) return true;
draw(x, y, t, 0);// 恢复现场
}
return false;
}
int main()
{
for(int i = 0; i < N; i ++) map[1 << i] = i;// 先预处理出2的1 - 9次方的大小数字对应的1-9
for(int i = 0; i < 1 << N; i ++)// 预处理出1-511中每个数字有几个二进制1
for(int j = i; j > 0; j -= j & -j)
ones[i] ++;
while(cin >> str, str[0] != 'e'){
for(int i = 0; i < N; i ++) row[i] = col[i] = M - 1;// 先处理出每行,每列,每个九宫格的大小
for(int i = 0; i < 3; i ++)
for(int j = 0; j < 3; j ++)
cell[i][j] = M - 1;
int cnt = 0;
for(int i = 0, k = 0; i < N; i ++)// 将九宫格完善,同时统计出有几个空格
for(int j = 0; j < N; j ++, k ++)
if(str[k] != '.'){
int t = str[k] - '1';
draw(i, j, t, 1);
}else cnt ++;
dfs(cnt);
puts(str);
}
return 0;
}
从小到大枚举原始木棒的长度 len (也就是枚举答案)。当然, len 应该是所有木棍长度总和 sum 的约数 ,并且原始木棒的根数 cnt 就等于 sum / len
剪枝 1 : 优化搜索顺序 : 把木棍长度从大到小排序 (感觉像是减少高层次的树枝数量)
剪枝 2 : 排除等效冗余
(1) 可以限制先后加入一根原始木棒的木棍长度是递减的 (这是因为先拼上一根长度为 x 的木棍,再拼上一根长为 y 的木棍(x < y),与先拼上 y 再拼上 x 显然是等效的,只需要搜索其中一种)
(2)当一根木棍在某一个位置上拼接失败时,那么相同长度的木棍拼接在此处也是失败的
(3) 如果在当前原始木棒中 “尝试拼入的第一根木棍” 的递归分支返回失败,那么直接判定当前分支失败,立即回溯。这是因为在拼入这根木棍前,面对的原始木棒都是 ” 空 “的(还没有进行拼接),这些木棒是等效的。木棍拼在当前的木棒中失败,拼在其它木棒中一样会失败。
(4) 如果在当前原始木棒中拼入一根木棍后,木棒恰好被拼接完整,并且 “接下来拼接剩余原始木棒” 的递归分支返回失败,那么直接判定当前分支失败,立即回溯,该剪枝可以用贪心来解释,”再用1跟木棍恰好拼完当前原始木棒” 必然比 “再用若干跟木棍拼完当前原始木棒” 更好。
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 110;
int len, sum, w[N], n;
bool st[N];
bool dfs(int cnt, int s, int u)
{
if(cnt * len == sum) return true;
if(s == len) return dfs(cnt + 1, 0, 0); // 拼完当前木棒,新开一根木棒
for(int i = u; i < n; i ++){ // 剪枝 2(1)
if(st[i] || s + w[i] > len) continue;// 已经用过当前木棍或者拼上当前木棍超过当前的木棒长度
st[i] = 1;
if(dfs(cnt, s + w[i], i)) return true;
st[i] = 0;
if(!s || s + w[i] == len) return false; // 剪枝 2(3) 和 2(4)
int j = i;
while(j < n && w[j] == w[j + 1]){ // 剪枝 2(2)
j ++;
}
i = j;
}
return false;
}
int main()
{
while(cin >> n, n){
sum = 0;
for(int i = 0; i < n; i ++){ cin >> w[i];sum += w[i];}
// cout << sum << endl;
memset(st, 0, sizeof st);
sort(w, w + n);// 剪枝 1
reverse(w, w + n);
len = 1;
while(1){
if(sum % len == 0 && dfs(0, 0, 0)){
cout << len << endl;
break;
}else len ++;
}
}
return 0;
}
emmm… 下次补把


tql