bfs
emmm…感谢 y总 和 lyd大佬
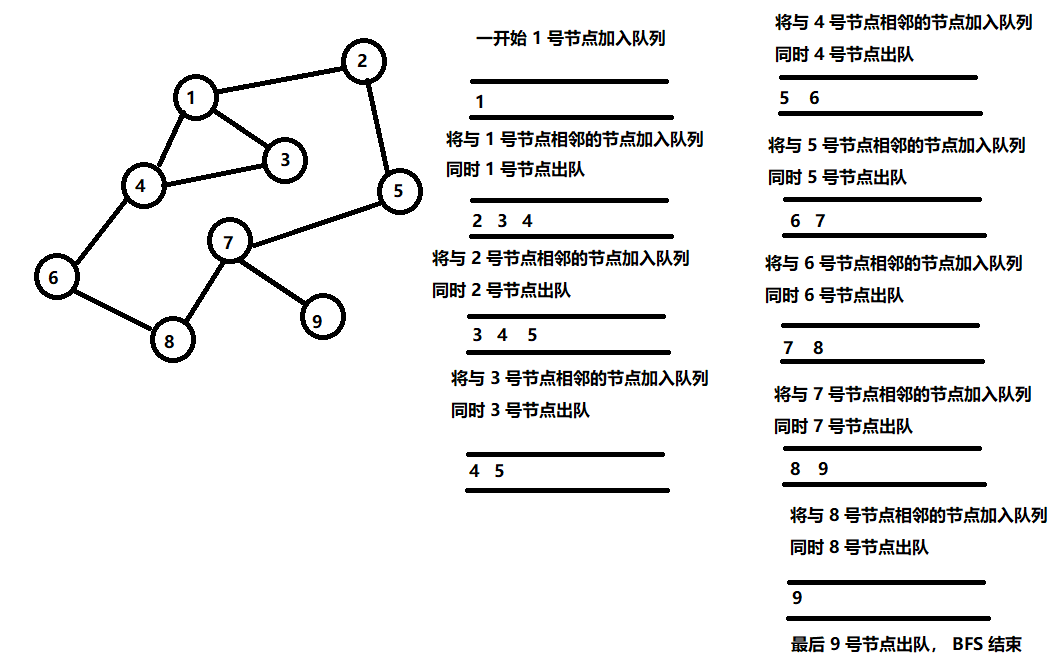
广度优先遍历需要使用一个队列来实现。起初,队列中仅包含一个起点(例如 1 号节点)。在广度优先遍历的过程中,我们不断从队头取出一个节点 x ,对于 x 面对的多条分支,把沿着每条分支到达的下一个节点 (如果尚未访问过) 插入队尾。重复执行上述过程直到队列为空。
void bfs()
{
memset(st, 0, sizeof st);
queue < int > q;
q.push(1);
st[1] = 1;
while(q.size()){
int u = q.front();
q.pop();
for(int i = h[u]; ~i; i = ne[i]){ // 遍历相邻的点
int v = e[i];
if(st[v]) continue; // 是否被访问过(是否满足条件)
st[v] = 1;
q.push(v);
}
}
}
在广度优先遍历的过程中顺便求出了一个 d 数组,对于一棵树来讲,d[x] 就是点 x 在树中的深度。对于一张图来讲,d[x] 被称为点 x 的层次 (从起点 1 走到点 x 需要经过的最少点数)。

广度优先遍历是一种按照层次顺序进行访问的方法,它具有两个重要性质
1、在访问完所有的第 i 层节点后,才会开始访问第 i + 1 层节点
2、任意时刻,队列中至多有两个层次的节点。若其中一部分节点属于第 i 层,则另一部分节点属于第 i + 1 层,并且所有第 i 层节点排在第 i + 1 层节点之前。
也就是广度优先遍历队列中的元素关于层次满足 “两段性” 和 “单调性”。
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<queue>
using namespace std;
const int N = 1e5 + 10, M = 2e5 + 10;
int h[N], ne[M], e[M], idx;
int n, m, d[N];
void add(int a, int b)
{
e[idx] = b, ne[idx] = h[a], h[a] = idx ++;
}
int bfs()
{
memset(d, -1, sizeof d);
queue < int > q;
q.push(1);
d[1] = 0;
while(q.size()){
int u = q.front();
q.pop();
for(int i = h[u]; ~i; i = ne[i]){
int v = e[i];
if(~d[v]) continue;
q.push(v);
d[v] = d[u] + 1;
}
}
return d[n];
}
int main()
{
cin >> n >> m;
memset(h, -1, sizeof h);
while(m -- ){
int a, b;
scanf("%d%d", &a, &b);
add(a, b);
}
cout << bfs() << endl;
return 0;
}
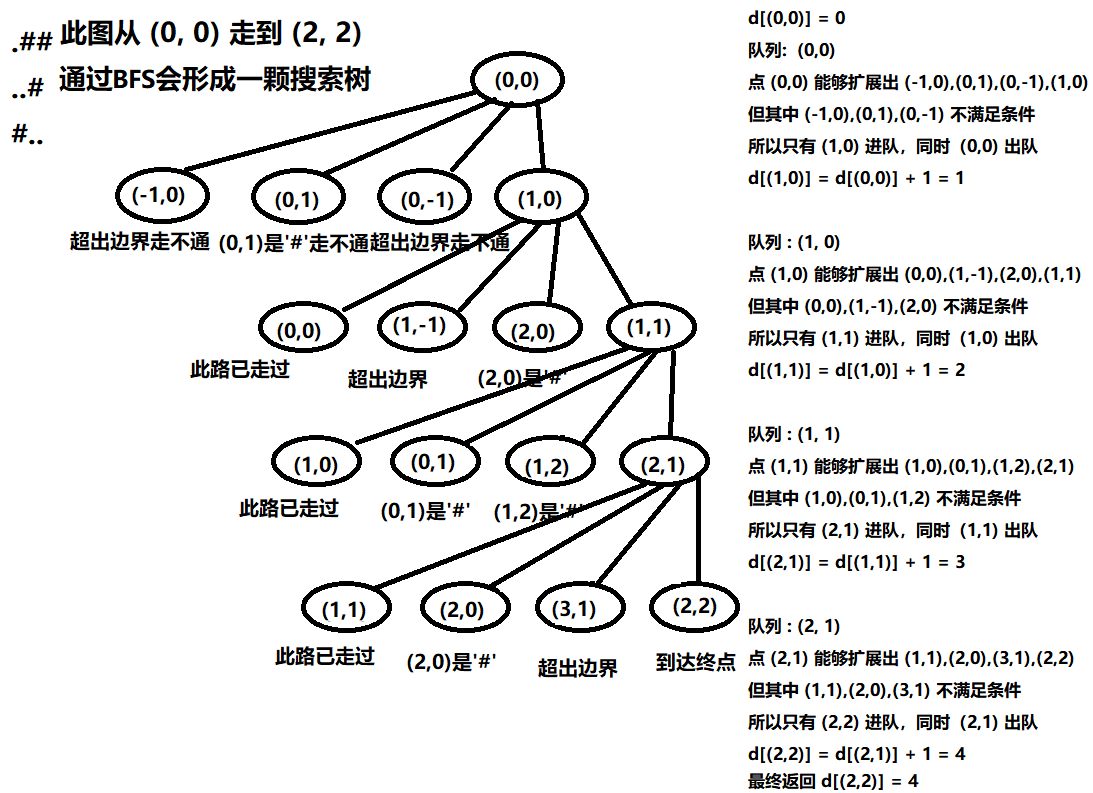
“走地图”类问题,也就是形如 “给定一个矩形地图,控制一个物体在地图中按要求移动,求最少步数”的问题。BFS很擅长解决这类问题——地图的整体形态是固定不变的,只有少数个体或特征随着每一步操作发生改变。我们只需要把这些变化的部分提取为状态,把起始状态加入队列,使用 BFS 不断取出队头状态,沿着分支扩展、入队即可。BFS 是逐层遍历搜索树的算法,所有状态按照入队的先后顺序具有层次单调性(也就是步数单调性)。如果每一次扩展恰好对应一步,那么当一个状态第一次被访问(入队)时,就得到了从起始状态到达该状态的最少步数。
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<queue>
using namespace std;
const int N = 110;
typedef pair < int , int > pii;
#define x first
#define y second
int n, m, g[N][N], d[N][N];
int dx[] = {1, 0, -1, 0};
int dy[] = {0, -1, 0, 1};
int bfs()
{
queue < pii > q;
q.push({0, 0});
memset(d, -1, sizeof d);
d[0][0] = 0;
while(q.size()){
pii t = q.front();
q.pop();
for(int i = 0; i < 4; i ++){
int nx = t.x + dx[i], ny = t.y + dy[i];
if(nx < 0 || nx >= n || ny < 0 || ny >= m) continue; // (nx, ny)是否满足条件
if(~d[nx][ny] || g[nx][ny]) continue;
d[nx][ny] = d[t.x][t.y] + 1;
q.push({nx, ny});
}
}
return d[n - 1][m - 1];
}
int main()
{
cin >> n >> m;
for(int i = 0; i < n; i ++)
for(int j = 0; j < m; j ++)
cin >> g[i][j];
cout << bfs() << endl;
return 0;
}
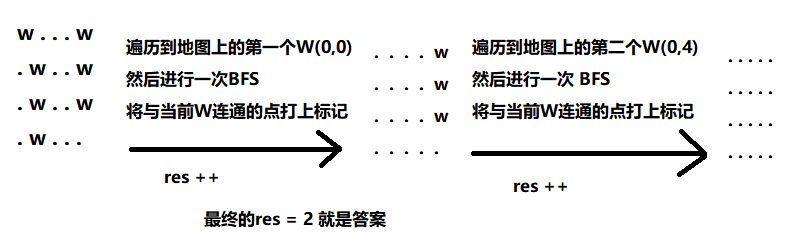
Flood Fill 模型
遍历 “地图” 上的每一个点如果当前点是 ‘W’ 的话,就以当前点为起点进行一次 BFS 将与当前点连通的地图改成 ‘.’ (或者打上标记)最后进行了几次 BFS 就是有几个连通块(也就是池塘个数)
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<queue>
using namespace std;
typedef pair < int , int > pii;
#define x first
#define y second
const int N = 1010;
char g[N][N];
int n, m;
int dx[] = {-1, -1, -1, 0, 0, 1, 1, 1};
int dy[] = {-1, 0, 1, -1, 1, -1, 0, 1};
void bfs(int x, int y)
{
queue < pii > q;
q.push({x, y});
while(q.size()){
pii t = q.front();
q.pop();
for(int i = 0; i < 8; i ++){
int nx = t.x + dx[i], ny = t.y + dy[i];
if(nx < 0 || nx >= n || ny < 0 || ny >= m) continue;
if(g[nx][ny] == '.') continue;
q.push({nx, ny});
g[nx][ny] = '.';
}
}
}
int main()
{
cin >> n >> m;
for(int i = 0; i < n; i ++) cin >> g[i];
int res = 0;
for(int i = 0; i < n; i ++) // 遍历地图上的每一个点
for(int j = 0; j < m; j ++){
if(g[i][j] == 'W'){
bfs(i, j);
res ++;
}
}
cout << res << endl;
return 0;
}
遍历地图中的每一个点,如果当前的点没有被打上标记,就进行 BFS 将与当前点连通的点都打上标记。
对于每一个点 可以将其看成 二进制的形式
每个方块中墙的特征由数字 PP 来描述,我们用1表示西墙,2表示北墙,4表示东墙,8表示南墙,PP 为该方块包含墙的数字之和。例如,如果一个方块的 PP 为3,则 3 = 1 + 2,该方块包含西墙和北墙。
比如 15 转换成 二进制的形式是 1111 就代表上下左右都有墙 12 转换成二进制的形式是 1010 就是代表 上下有两面墙
5 转换成二进制的形式是 0101 表示 左右两面墙。

最后进行了几次BFS 就是有多少个连通块 (房间) 每次 BFS 统计有多少个点进入队列,就是每个连通块的大小,最后在其中取一个最大值
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<queue>
using namespace std;
typedef pair < int , int > pii;
#define x first
#define y second
const int N = 55;
int n, m, g[N][N];
bool st[N][N];
int dx[] = {0, -1, 0, 1}; // 要定义成 左上右下的顺序
int dy[] = {-1, 0, 1, 0};
int bfs(int x, int y)
{
queue < pii > q;
q.push({x, y});
st[x][y] = 1; // 标记每个点
int res = 1; // 表示每个连通块的大小
while(q.size()){
pii t = q.front();
q.pop();
for(int i = 0; i < 4; i ++){
int nx = t.x + dx[i], ny = t.y + dy[i];
if(nx < 0 || nx >= n || ny < 0 || ny >= m) continue; // 判断是否满足条件
if(g[t.x][t.y] >> i & 1) continue;
if(st[nx][ny]) continue;
q.push({nx, ny});
st[nx][ny] = 1;
res ++; // 每进队一次就要让连通块的大小加 1
}
}
return res;
}
int main()
{
cin >> n >> m;
for(int i = 0; i < n; i ++)
for(int j = 0; j < m; j ++)
cin >> g[i][j];
int res = 0, ans = 0;
for(int i = 0; i < n; i ++)
for(int j = 0; j < m; j ++){
if(!st[i][j]){
res ++;
ans = max(ans, bfs(i, j));
}
}
cout << res << endl << ans << endl;
return 0;
}
最短路模型
这个题目可以在走迷宫的基础上记一个数组 pre 表示当前点是由那个点转移而来的 pre[(nx, ny)] = (x, y)
比如 (2, 1) 可以移动到 (2, 2) pre 数组就可以表示为 pre[(2, 2)] = (2, 1)
最后可以通过循环还原整条路径
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<queue>
using namespace std;
typedef pair < int , int > pii;
#define x first
#define y second
const int N = 1010;
int g[N][N], n;
bool st[N][N];
pii pre[N][N];
int dx[] = {-1, 0, 1, 0};
int dy[] = {0, -1, 0, 1};
void bfs(int x, int y)
{
queue < pii > q;
q.push({x, y});
st[x][y] = 1;
while(q.size()){
pii t = q.front();
q.pop();
for(int i = 0; i < 4; i ++){
int nx = t.x + dx[i], ny = t.y + dy[i];
if(nx < 0 || nx >= n || ny < 0 || ny >= n) continue;
if(st[nx][ny] || g[nx][ny]) continue;
pre[nx][ny] = {t.x, t.y}; // 记录路径
st[nx][ny] = 1;
q.push({nx, ny});
}
}
}
int main()
{
cin >> n;
for(int i = 0; i < n ; i ++)
for(int j = 0; j < n; j ++)
scanf("%d", &g[i][j]);
bfs(n - 1, n - 1);
pii end = {0, 0}; // 还原路径
while(1){
printf("%d %d\n", end.x, end.y);
if(end.x == n - 1 && end.y == n - 1) break;
end = pre[end.x][end.y];
}
return 0;
}
emmm .... 在走迷宫的问题上改变搜索的顺序同时改变起点和终点的位置 起点为 K, 终点为 H
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<queue>
using namespace std;
typedef pair < int , int > pii;
#define x first
#define y second
const int N = 155;
char g[N][N];
int n, m, dis[N][N];
int dy[] = {-2, -1, 1, 2, 2, 1, -1, -2};
int dx[] = {-1, -2, -2, -1, 1, 2, 2, 1};
int bfs(int x, int y)
{
queue < pii > q;
q.push({x, y});
dis[x][y] = 0;
while(q.size()){
pii t = q.front();
q.pop();
for(int i = 0; i < 8; i ++){
int nx = t.x + dx[i], ny = t.y + dy[i];
if(nx < 0 || nx >= n || ny < 0 || ny >= m) continue;
if(dis[nx][ny] || g[nx][ny] == '*') continue;
if(g[nx][ny] == 'H') return dis[t.x][t.y] + 1;
dis[nx][ny] = dis[t.x][t.y] + 1;
q.push({nx, ny});
}
}
}
int main()
{
cin >> m >> n;
for(int i = 0; i < n; i ++) cin >> g[i];
int x, y;
for(int i = 0; i < n; i ++)
for(int j = 0; j < m; j ++)
if(g[i][j] == 'K') x = i, y = j;
cout << bfs(x, y) << endl;
return 0;
}
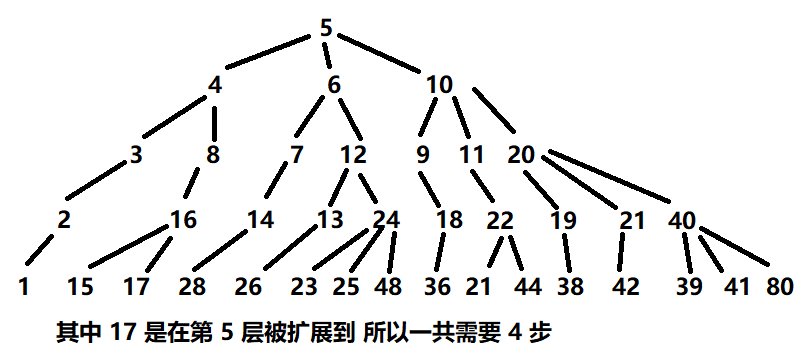
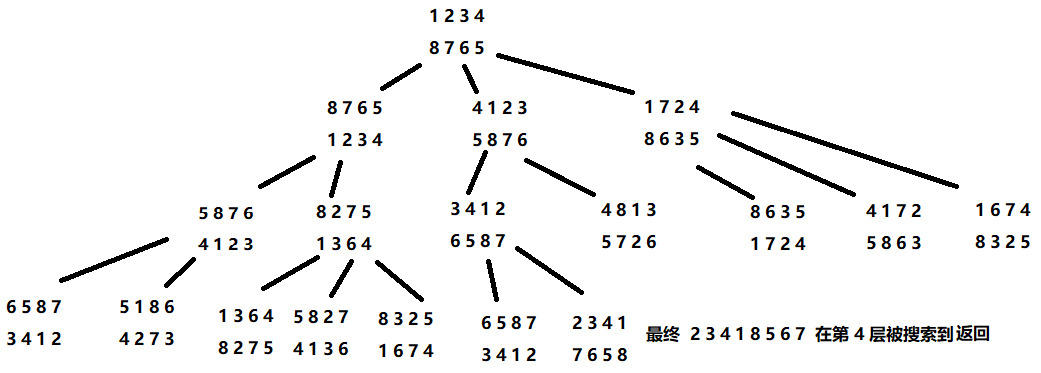
这个题目不再像走迷宫那样将二维坐标看成一个状态,而是将一个数字看成是一个状态,状态之间的变换就是一次可用的移动方式
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<queue>
using namespace std;
const int N = 2e5 + 10;
int dis[N], n, k;
void bfs()
{
queue < int > q;
q.push(n);
dis[n] = 0;
while(q.size()){
int t = q.front();
q.pop();
if(t + 1 <= N && !dis[t + 1]) q.push(t + 1), dis[t + 1] = dis[t] + 1;
if(t - 1 >= 0 && !dis[t - 1]) q.push(t - 1), dis[t - 1] = dis[t] + 1;
if(t * 2 <= N && !dis[t * 2]) q.push(t * 2), dis[t * 2] = dis[t] + 1;
}
}
int main()
{
cin >> n >> k;
bfs();
cout << dis[k] << endl;
return 0;
}
多源BFS
这个题目可以看作一道有多个起始状态的Flood - Fill 问题。我们把矩阵 A 中每一个 1 都看作起点,整个矩阵的所有位置都可以通行,对于每个位置,在从任何一个起点触发都可以的情况下,求到达该位置所需要的最少步数(也就是距离该位置最近的起点的距离)
在这种具有多个等价的起始状态的问题中,我们只需要在 BFS 开始之前把这些起始状态全部插入队列
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<queue>
using namespace std;
typedef pair < int , int > pii;
#define x first
#define y second
const int N = 1010;
char g[N][N];
int n, m, dis[N][N];
int dx[] = {0, -1, 0, 1};
int dy[] = {-1, 0, 1, 0};
void bfs()
{
memset(dis, -1, sizeof dis);
queue < pii > q;
for(int i = 0; i < n; i ++) // 一开始将所有的起点加入队列
for(int j = 0; j < m; j ++)
if(g[i][j] == '1'){
dis[i][j] = 0;
q.push({i, j});
}
while(q.size()){
pii t = q.front();
q.pop();
for(int i = 0; i < 4; i ++){
int nx = t.x + dx[i], ny = t.y + dy[i];
if(nx < 0 || nx >= n || ny < 0 || ny >= m) continue;
if(~dis[nx][ny]) continue;
dis[nx][ny] = dis[t.x][t.y] + 1;
q.push({nx, ny});
}
}
}
int main()
{
cin >> n >> m;
for(int i = 0; i < n; i ++) cin >> g[i];
bfs();
for(int i = 0; i < n; i ++){
for(int j = 0; j < m; j ++)
cout << dis[i][j] << " ";
cout << endl;
}
return 0;
}
可以将整个模板看成一个状态,状态之间的转移就是一次可用的操作方式
然后可以将模板看成一个字符串,从左上角开始沿着顺时针的方向,环绕一周取出每个数字
比如 2 3 4 1 可以看成 2 3 4 1 8 5 6 7 这样的字符串
7 6 5 8
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<queue>
#include<unordered_map>
using namespace std;
const int N = 10;
unordered_map < string , int > dis;
unordered_map < string , pair < char , string > > pre;
string end1, start, res;
char g[3][5];
void set(string t)
{
for(int i = 0; i < 4; i ++) g[0][i] = t[i];
for(int j = 4, i = 3; i >= 0; i --, j ++)
g[1][i] = t[j];
}
string get()
{
string res;
for(int i = 0; i < 4; i ++) res += g[0][i];
for(int i = 3; i >= 0; i --) res += g[1][i];
return res;
}
string move0(string t) // 操作 A
{
set(t);
for(int i = 0; i < 4; i ++)
swap(g[0][i], g[1][i]);
return get();
}
string move1(string t) // 操作 B
{
set(t);
char a0 = g[0][3], a1 = g[1][3];
for(int i = 3; i > 0; i -- ){
g[0][i] = g[0][i - 1];
g[1][i] = g[1][i - 1];
}
g[0][0] = a0;
g[1][0] = a1;
return get();
}
string move2(string t) // 操作 C
{
set(t);
char x = g[0][1];
g[0][1] = g[1][1];
g[1][1] = g[1][2];
g[1][2] = g[0][2];
g[0][2] = x;
return get();
}
int bfs()
{
if(start == end1) return 0;
queue < string > q;
q.push(start);
dis[start] = 0;
string m[5];
while(q.size()){
string t = q.front();
q.pop();
m[0] = move0(t);
m[1] = move1(t);
m[2] = move2(t);
for(int i = 0; i < 3; i ++){
// cout << m[i] << endl;
if(dis.count(m[i])) continue; // 是否已经被访问过
dis[m[i]] = dis[t] + 1;
pre[m[i]] = {i + 'A', t};
q.push(m[i]);
if(m[i] == end1) return dis[end1];
}
}
}
int main()
{
for(int i = 1; i <= 8; i ++){
int x;
cin >> x;
end1 += x + '0';
}
start = "12345678";
// set(start);
// for(int i = 0; i < 4; i ++) cout << g[0][i];
// cout << endl;
// for(int i = 0; i < 4; i ++) cout << g[1][i];
int ans = bfs();
cout << ans << endl;
while(end1 != start){
res += pre[end1].first;
end1 = pre[end1].second;
}
reverse(res.begin(), res.end());
if(ans > 0) cout << res << endl;
return 0;
}
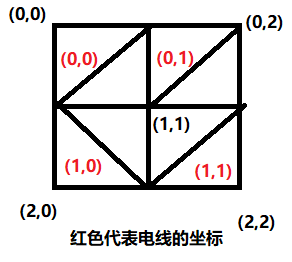
这是一张边权要么是 0,要么是 1 的无向图。在这样的图上,我们可以通过双端队列广搜来计算。算法的整体框架与一般的广搜类似,只是在每个节点上沿分支扩展时稍作改变。如果这条分支时边权为 0 的边,就把沿该分支到达的新节点从队头入队;如果这条分支时边权为 1 的边,就像一般的广搜一样从队尾入队。这样一来,我们就任然能保证,任意时刻广搜队列中的节点对应的距离值都具有“两段性”和“单调性”,每个节点虽然可能被更新(入队)多次,但是它第一次被扩展(出队时),就能得到从左上角到该节点的最短距离,之后再被取出可以直接忽略。
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<queue>
using namespace std;
typedef pair < int , int > pii;
#define x first
#define y second
const int N = 510;
char g[N][N], s[] = "\\/\\/";
int dx[] = {-1, -1, 1, 1};
int dy[] = {-1, 1, 1, -1};
int ix[] = {-1, -1, 0, 0};
int iy[] = {-1, 0, 0, -1};
int dis[N][N], n, m, T;
bool st[N][N];
int bfs()
{
memset(dis, 0x3f, sizeof dis);
memset(st, 0, sizeof st);
deque < pii > q;
q.push_front({0, 0});
dis[0][0] = 0;
while(q.size()){
pii t = q.front();
q.pop_front();
if(st[t.x][t.y]) continue;
st[t.x][t.y] = 1;
if(t.x == n && t.y == m) return dis[n][m];
for(int i = 0; i < 4; i ++){
int nx = t.x + dx[i], ny = t.y + dy[i];
if(nx < 0 || nx > n || ny < 0 || ny > m) continue;
int wx = t.x + ix[i], wy = t.y + iy[i];
int w = (g[wx][wy] != s[i]);
if(dis[nx][ny] > dis[t.x][t.y] + w){
dis[nx][ny] = dis[t.x][t.y] + w;
if(w) q.push_back({nx, ny});
else q.push_front({nx, ny});
}
}
}
}
int main()
{
cin >> T;
while(T --){
cin >> n >> m;
for(int i = 0 ; i < n; i ++) cin >> g[i];
if((n + m) & 1) puts("NO SOLUTION");
else{
int ans = bfs();
cout << ans << endl;
}
}
return 0;
}

