筛质数
aciwng1292
筛出n以内的质数,从小到大枚举出第一对满足的数。时间复杂度,O(n+n/lnn)
code
acwing1293
一件珠宝的价格是另一件珠宝的价格的质因子时,两件珠宝的颜色不同。
即从一个质数向合数连一条边,最后会构成二分图(质数之间彼此互质没有连边,合数之间不满足一个数是另一个的质因子也没有连边),当n<=2时只有质数,输出1,由二分图可知其他情况均为2
code
acwing196
L,R的范围很大,但是R-L的范围很小,并且任何一个合数必定包含一个不超过sqrt(n)的质因子
1.筛出2~sqrt(R)之间的所有质数
2.对于每个质数P,把[l,r]中内被p整除的数标记
3.最终所有未被标记的数就是[l,r]中所有质数,对相邻两数枚举比较找差值最大的即可。
时间复杂度:筛质数为$O(\sqrt{R})$,标记非质数的时间复杂度为$O(\sqrt{R}loglog\sqrt{R})$,
code
细节:1.如何找到大于等于L的最小的P的倍数P0?
L/P向上取整 P,即 P0=[(L+P-1)/P]下取整 P
2.至少是P0的两倍才能将其标记为false
3.l,r范围太大,标记时将其离散化
acwing197
$n!=1\times2\times…\times n$
若把1-n每个数分别分解质因数再整合出n!分解质因数的结果,时间复杂度为$O(n\sqrt{n})$
逆向思考,n!的每个质因子都不会超过n,
1.先筛出1-n的每个质数p
2.在1~n中,p的倍数,即至少包含1个质因子p的有n/p个,包含$p^2$的有n/$p^2$,不过其中一个质因子已经在n/p里统计过,只需再统计第二个质因子,即累加上n/$p^2$,而不是2*n/$p^2$

code
快速幂
acwing1289
一个数列即等差又等比 <-> 常数数列
证明: a b c
前提:a!=b!=c
根据数列性质求解:
a+c=2b,ac=b^2 =>必然有 b=c 所以a=b=c 常数数列
code
acwing1290
监狱有连续编号为 1 到 n 的 n个房间,每个房间关押一个犯人。有 m种宗教,每个犯人可能信仰其中一种。
如果相邻房间的犯人信仰的宗教相同,就可能发生越狱。求有多少种状态可能发生越狱。
所有宗教信仰情况为$m^n$,第一个人有m中选择,剩下的n-1个人有m-1种选择
故答案为$m^n-m*(m-1)^{n-1}$
code
约数个数
acwing1294
给定一个整数 n,求有多少正整数数对 (x,y) 满足 1/x+1/y=1/n!。
$\frac{(x+y)}{xy} = \frac1{n!}$
$y=\frac{xn!}{x-n!} 得 (x-n!) | xn!$
y是正整数,则x>n!
继续化简,
y=n!+ n!^2/(x-n!)
得 (x-n!) | n!^2
只要确定了$n!^2$的约数有哪些,x则确定,x一旦确定y也随即确定
经过转化后求$n!^2$的约数个数即为满足要求的x,y对数
类比acwing197的方法可求出n!分解质因数的结果,
这里求的是$n!^2$,只需次数*2即可
code
acwing198
性质1:
1~n中最大的反质数,就是1~n中约数个数最多的数中最小的一个

性质2:

性质3:
前10个素数的积> 2×1e9,所以最多用到9个素数
使用暴搜确定前9个质数的指数,满足指数单调递减,总乘积不超过n,同时记录约数个数。
每当搜索处一个满足条件的整数,更新约数个数最多的数中最小的一个。
code
acwing200
已知正整数a,b,c,d,求有多少个x满足gcd(a,x)=c,并且lcm(b,x)=d

code
欧拉函数
acwing201
给你一个n * n的网格,任意一点和(0,0)连线,可以组成一条直线,前面的点可以挡住后面的点,问你能看到的点到底有多少个?
思路分析:题目实际上就是问在这个网格上有多少种不同的斜率,坐标轴上的两点我们先不管,然后将整个正方形分成上三角和下三角两部分,由对称性,两边可以看到的点的数目肯定一样多,以下三角为例进行研究,我们会发现,对于所有能看到的点,他们有着一个共同的特征,那就是gcd(x,y)=1,若不为1,则他前面肯定有一个点挡住了这个点,那么本题就转变成了一个求欧拉函数和的简单题目,最后加上y=x上的一个点和坐标轴上的两个点,本题答案就是3+2*∑φ(i) (i : 2~n)
code
acwing220
要求gcd(x, y) = p (1 <= x, y <= n, p为质数 ) 的数对(x, y)个数.我们枚举素数p, 令x’ = x / p, y’ = y / p, 则只须求 f(p) = gcd(x’, y’) = 1的数对(x’, y’)个数(1 <= x’, y’ <= n / p), 显然f(p) = (∑ phi(x’)) * 2 - 1(1 <= x’ <= n / p).x == y的情况即x=y=1(phi[1]=1)计算了两次故减去。 所以最后答案为 ∑f(p)
code
acwing202
现在给定一个正整数L,请问至少多少个8连在一起组成的正整数(即最小幸运数字)是L的倍数。

由欧拉定理可知,当q与10互质的时候,$10^{φ(q)}$=1 (mod q),即必定存在一个解x。
而题目中要求的是最小的解,设为min,那么有$a^{min}$=1(mod q),因为要满足$a^{φ(q)}$=1(mod p),那么$a^{φ(q)}$肯定能变换成$(a^{min})^i$。
所以接下来只要枚举φ(q)的因子,找出符合条件的最小者即可。
无解的时候就是q与10不互质的时候,因为若q与10有公因子d:
1.若d=2,q=2 * k,那么$10^x=2^x *5^x=1(mod 2k)$
即$2^x * 5^x=1+2k * m$,左边为偶数,右边为奇数,显然矛盾。
2.若d=5,q=5 * k,那么$10^x=2^x * 5^x=1(mod 5k)$
即$2^x * 5^x=1+5k * m$,左边是5的倍数,右边不是5的倍数,显然矛盾。
code
矩阵乘法
中国剩余定理
某些计数问题或数论问题出于加长代码、增加难度、或者是一些其他不可告人的原因,给出的模数: 不是质数 !
但是对其质因数分解会发现它没有平方因子,也就是该模数是由一些不重复的质数相乘得到。
那么我们可以分别对这些模数进行计算,最后用 CRT 合并答案。
P2480
莫比乌斯反演
hdu1695
给出n,m,k,求有多少个无序数对(x, y) 满足 x ∈[1,n],y ∈ [1,m],且 gcd(x, y) == k。
n,m,k ≤ 1e7
例如 n = 3, m = 5, k = 1
答案是 9 : (1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (2, 3), (2, 5), (3, 4), (3, 5).
首先发现题目可以转化为:
求有多少个数对(x, y) 满足 x ∈ [1,n/k],y ∈ [1,m/k], 且 gcd(x, y) == 1。 令 n’= n / k, m’= m / k。
我们可以先不考虑无序数对的问题,先算有序数对
问题可以写成: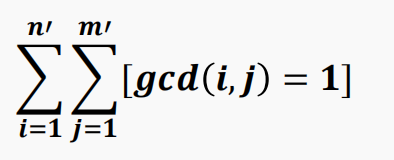
联系一个式子: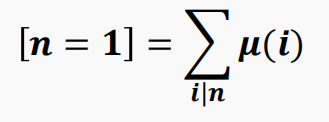
问题可以写成: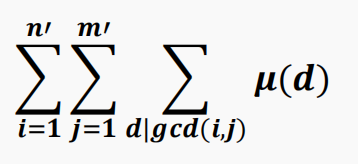
可以进一步写成: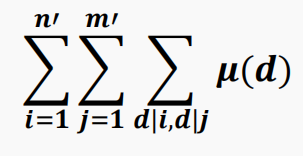
把 d 移到最前面来: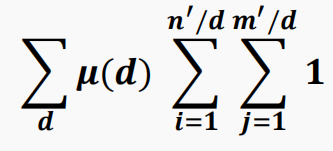
进一步等价于: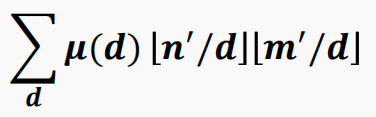
注意到 𝒏′/𝒅 𝒎′/𝒅 这个式子,连续一段的取值是相同的。
假设 n = 10, m = 12

形式化的来说,n / d = k 时: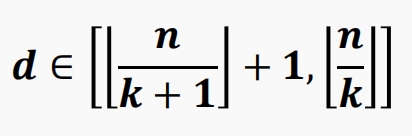
对于 n 来说,n / d 一共有 O(sqrt(n)) 段相同的值。
对于 n, m 来说,(n/d)(m/d) 一共也有 O(sqrt(n)) 段相同的值。
这样我们就可以求出 μ的前缀和,相同的一段值一起算。
从单次询问 O(n) 优化到了 单次询问O(sqrt(n))
最后不要忘记把算了两次的数对减掉。
code
题目中说明了,(1,2)和(2,1)算一种情况,由于我们规定b为较小者,故无需处理该情况,那么我们只需减去
(1,1),(2,2)等多余了的情况,怎那么找出那些多算进去的情况呢? 下面的图画的很清楚:
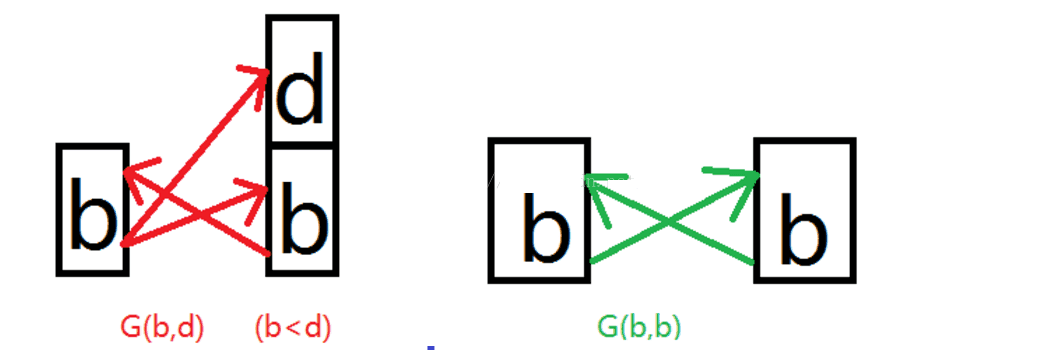
组合数学
集合的排列
令 r 为正整数,我们把 n 个元素的集合 S 的一个 r-排列
理解为 n 个元素中的 r 个元素的有序摆放。
如果 S = {a, b, c},则 S 的 3 个 1-排列是: a b c
S 的 6 个 2-排列是:ab ac ba bc ca cb
S 的 6 个 3-排列是:abc acb bac bca cab cba
我们用 A(n, r) 来表示 n 个元素集合 r-排列的数目。
如果 r > n,则 A(n, r) = 0
之前我们已经看到 A(3,1) = 3, A(3,2) = A(3,3) = 6
一般的,𝐴 𝑛, 𝑟 = 𝑛 × 𝑛 − 1 × ⋯ 𝑛 − 𝑟 + 1
也可以记为,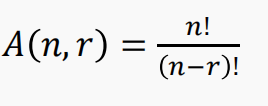
【例1】将 26 个字母排序,使得元音字母 a, e, i, o, u中任意两个都不得相继出现,问方案数。
【解】首先我们需要对辅音字母排序。总共有 21 个辅音字母,这个排列数是 21!
由于不能有两个元音字母连续出现,所以这些元音字母必须放入 22 个空位中。对 a 有 22 个位置,对 e 有 21 个位
置……也就是这一步可以有 A(22, 5) 种方法。
总共的方案数就是 21! * 22! / 17!
集合的循环排列
刚刚考虑的过的排列可以称为线性排列。
如果把它们排成一个圆,那么排列的数目就要减少。
思考一个问题,假设 6 个人排成一个圈,有几种不同的方式。
由于他们是一个圈,所以重要的是他们彼此之间的相对位置。
因此如果两个循环排列通过一个旋转可以从一个变成另外一个,那么要把它们两个看成是相同的。
例如 123456, 234561, 345612, 456123, 561234,612345 是等价的。
可以看出,6个人的线性排列和6个人的循环排列存在一个 6 到1的对应。因此只要用 6 去除线性排列的数目即可。
也就是 6!/6 = 5!
更一般的,n 个元素的集合的循环r-排列的个数是: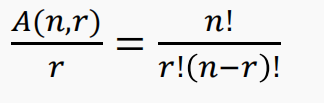
【例2】10个人要围坐一圆桌,其中有两人不愿意彼此挨着就坐。共有多少循环座位排放方案?
【解】先考虑 9 个人(X,3,4,…,9,10)的方案数:8!(9!/9)
然后 X 可以用 1,2 或 2,1 替换。因此挨着就坐的方案数是 28!
总方案数就是 9!-28!
集合的组合
令 r 为非负整数,我们把 n 个元素的集合 S 的一个 r-组合理解为从 S 的 n 个元素中对 r 个元素的无序选择。
如果 S = {a, b, c, d},则 S 的 4 个 3-组合是:
{a, b, c}, {a, b, d}, {a, c, d}, {b, c, d}
我们用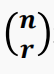
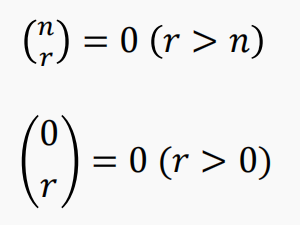
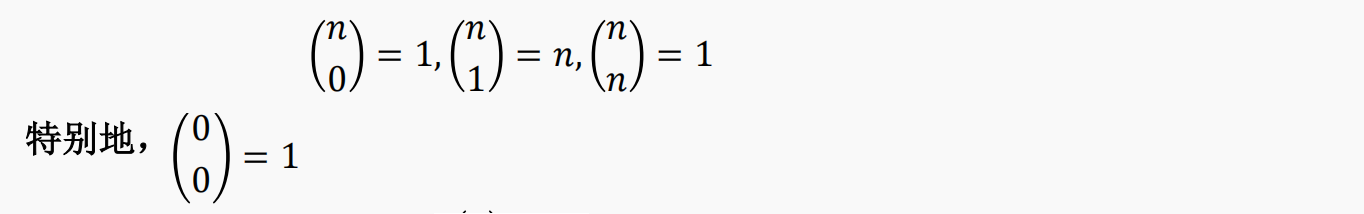
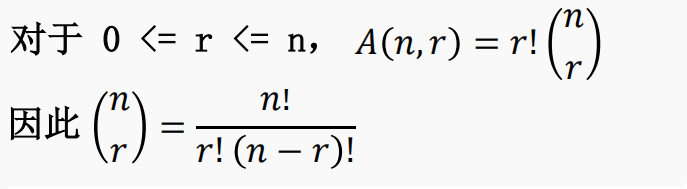
【例3】在平面上给出 25 个点,没有 3 个点共线。这些点能确定多少条直线?确定多少个三角形?
【解】每一对点确定唯一一条直线。因此答案为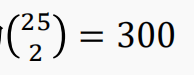
同理,每 3 个点确定唯一一个三角形,答案为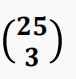
【例4】如果每个词包含 3、4或5个元音,那么用26个字母可以构造多少个8-字母词?
【解】首先分元音个数计数。3元音词:元音的位置有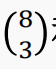
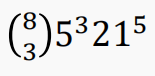
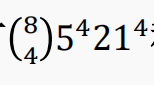
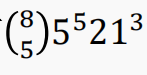
组合数的重要性质
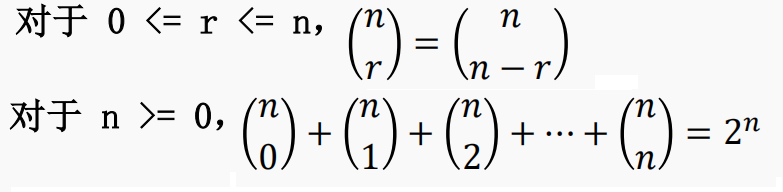
放小球
将n个不同的球放到m个不同的袋子里有多少种方案?对10^9+7取模。
直接输出$m^n$
将n个相同的球放到m个不同的袋子里有多少种方案?
考虑从一排n+m-1个元素中选出m-1个,这m-1个元素将序列分成了m段,第i段的元素个数就是第i个袋子中球的个数。
不难发现选元素的方案和放球的方案一一对应,因此方案数就是$C_{n-1}^{m-1}$。
将n个不同的球放到m个相同的袋子里有多少种方案?对10^9+7取模。
用f[i][j]表示将i个不同的球放到j个相同的袋子,并保证每个袋子里都有球的方案数。
考虑第i个球是不是单独放的。
f[i][j]=f[i-1][j-1]+f[i-1][j]*j。
如果允许空袋子,答案是f[n][0]+f[n][1]+…+f[n][m]。
时间复杂度O(nm)
将n个相同的球放在m个相同的袋子里有多少种方案?
f[i][j]=f[i-j][j]+f[i][j-1].时间复杂度O(nm)
平面分割
平面内有n条直线,最多可以把这个平面划分成多少区域?
考虑到这条线如果跟之前的每一条直线都相交,就会产生n个新的区域。
所以就很简单了!f[n]=f[n-1]+n
由于这个递推关系只涉及了相邻两项,我们可以用高中的累加法得到通项:f[n]=n*(n+1)/2+1
同一平面内有n(n≤500)条直线,已知其中p(p≥2)条直线相交于同一点,则这n条直线最多能将平面分割成多少个不同的区域?
由于共点直线的特殊性,我们决定先考虑p条相交于一点的直线,然后再考虑剩下的n-p条直线。
首先可以直接求出,p条相交于一点的直线将平面划分成的区域数为2p个;
然后在平面上已经有k(k≥p)条直线的基础上,再加上一条直线,最多可以与k条直线相交,而每次相交都会增加一个区域,与最后一条直线相交后,由于直线可以无限延伸,还会再增加一个区域。所以fi=fi-1+i(i>p),边界条件在前面已经计算过了,是fp=2p。
f(p)=2*p
f(i)=f(i-1)+i (i>p)
平面内有n条封闭曲线,任意两条封闭曲线交于两点,任意三条封闭曲线不交于一点,求划分出的区域数量?
记n条曲线划分出来的区域数量为f[n]
n条曲线被前n-1条曲线分割成2(n-1)段弧线
每一段弧线又会将一个区域划分出两个区域,所以是比原来多了2(n-1)个区域
f[n]=f[n-1]+2(n-1)
通过喜闻乐见的累加法,我们得到了通项:
f[n]=n^2-n+2
多重集合的排列
多重集是指包含重复元素的广义集合。设S={n1 * a1, n2 * a2 ,…,nk * ak}是有n1个a1,n2个a2,…,nk个ak组成的多重集。S的全排列个数为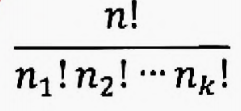
如果 S 是一个多重集,那么 S 的一个 r-排列是 S 的 r个元素的一个有序排放。如果 S 的元素总个数是 n (包括
计算重复元素),那么 S 的 n-排列也将称为 S 的排列。
例如 S = {a,a,b,c,c,c},那么 acbc,cbca 都是 S 的4-排列,abaccc,cbcaca 都是 S 的排列
令 S 是一个多重集,它有 k 个不同类型的元素,每一个元素都有无限重复次数,那么 S 的r-排列的个数为$k^r$
令 S 是一个多重集,有 k 个不同类型的元素,各元素的重数分别为 n1,n2,…,nk。 设 S 的大小为 n1+n2+…+nk,则 S 的排列数等于: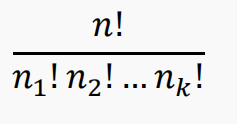
【例】计算 mississippi 中的字母排列数。
【解】{1M, 4I, 4S, 2P} 的排列数,11!/4!4!2!1!
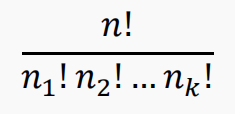
考虑4个元素的集合{a,b,c,d},它要被划分成两个集合,每个集合的大小为2. 如果这两部分没有标签,那么有三种划
分方式:ab/cd, ac/bd, ad/bc。
如果有标签,比如有黑色和白色,那么ab/cd就对应两种方案:黑ab/白cd,白ab/黑cd


非攻击型车问题
在8 * 8的国际象棋棋盘上,两个车能够相互攻击的充要条件是它们位于棋盘的同一行或同一列。
现在的问题是:在8 * 8的额棋盘上对于8个非攻击型车有多少种可能的方法?
我们给棋盘上的每个方块一对坐标 (i, j)。 8个车的坐标一定是 (1,j1),(2,j2),…,(8,j8) 且 j 是 {1,2,…,8} 的排列。
因此答案就是 8!
在上面的例子中,我们假设每个车都是等价的。如果 8 辆车各不相同,方案数是多少呢?
我们只要先摆放好,然后决定一个颜色的排列即可。方案数是8!8!
假设有 2 个红车,3 个绿车, 3个蓝车,问方案数?
染色的方案数是 8!/(2!3!3!),乘上车的摆放方案就是 8!8!/(2!3!3!)
有 n 个车共 k 种颜色,第一种颜色的车有 n1 个,第二种颜色的车有 n2 个,…,第 k 种颜色的车有 nk 个。
将这些车摆放在 n * n 的棋盘上,使没有车能够互相攻击的摆放方法数等于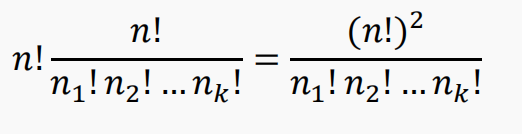
多重集合的组合
设S={n1 * a1, n2 * a2 ,…,nk * ak} 是有n1个a1,n2个a2,…,nk个ak组成的多重集。设整数r<=ni(i∈[1,k]) 从S中取出r个元素组成一个多重集(不考虑元素的顺序),产生的不同多重集的数量为: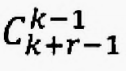
如果 S 是一个多重集,那么 S 的一个 r-组合是 S 的 r个元素的一个无序选择。
如果 S 的元素总个数是 n (包括计算重复元素),那么 S只有一个 n-组合;如果 S 含有 k 种不同类型的元素,那么就存在 S 的 k 个1-组合。
令S为具有k种类型元素的一个多重集,每种元素均具有无限
的重复数。则S的r-组合的个数为: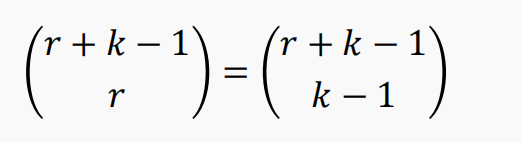
假设第i种类型选xi个,这里的个数即为 x1+x2+…+xk = r 的非负整数解的个数。
运用隔板法可以求得
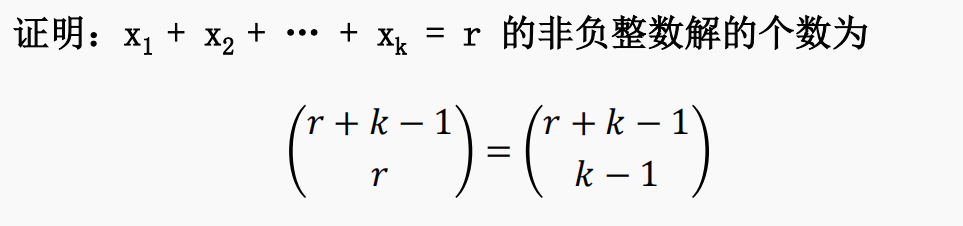
如果我们考虑正整数解,那么方案数为$C_{r-1}^{k-1}$
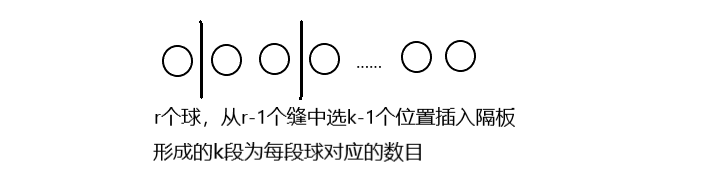
若求非负整数解,则两个隔板可插在同一个位置(因为某段小球的数量可为0)
不妨设yi=xi+1,则∑yi=r+k(i:1~k),可以发现yi>1,则方案数为$C_{r+k-1}^{k-1}$
【例】一家面包房生产 9 种炸面包圈,如果一盒内装有 12个面包圈,那么你能买到多少种不同的盒装面包圈?
【解】
【例】 S 集合里 a,b,c,d 各有 10 个,求有几个 10-组合满足a,b,c,d都至少出现一次
【解】x1 + x2 + x3 + x4 = 10 的正整数解的个数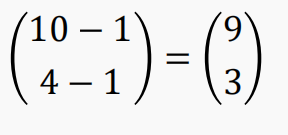
【例】方程 x1 + x2 + x3 + x4 = 20 的整数解有多少?其中:x1 >= 3, x2 >= 1, x3 >= 0, x4 >= 5
【解】令 y1 = x1 - 3, y2 = x2 - 1, y3 = x3, y4 = x4 - 5 y1 + y2 + y3 + y4 = 11
二项式系数
之前已经介绍了$C_n^k$表示n个元素的集合中k-组合的个数。
由于它们出现在二项式定理中,因此它们也叫二项式系数。
Pascal公式
对于满足 1 <= k <= n-1 的所有整数 k 和 n,$C_n^k=C_{n-1}^{k-1}+C_{n-1}^{k}$
另外,对于 n >= 0,$C_n^0=C_n^n=0$
预处理二项式系数
int c[N][N];
for (int i = 0; i <= n; i ++){
c[i][0] = c[i][i] = 1;
for (int j = 1; j < i; j ++)
c[i][j] = c[i - 1][j - 1] + c[i][j - 1];
}
二项式定理


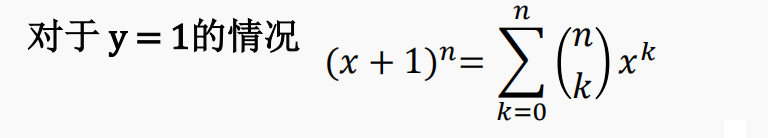
常见的恒等式
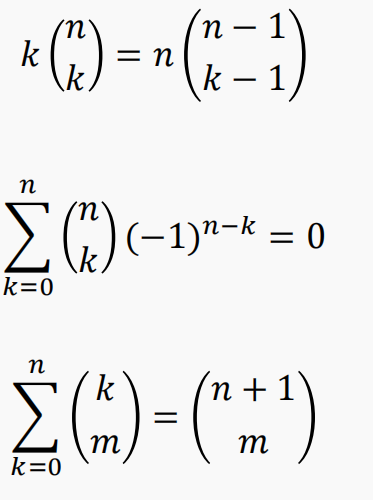
$∑(C_n^i)^2$=$C_{2n}^{n}$ i:0~n
多项式系数
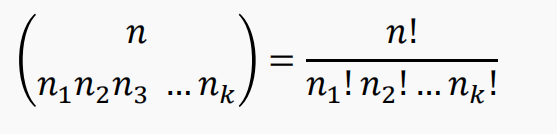
这里,𝑛1 𝑛2 𝑛3 … 𝑛𝑘 都是非负整数,且𝑛1 +𝑛2 +𝑛3 + … +𝑛𝑘= 𝑛
多项式定理
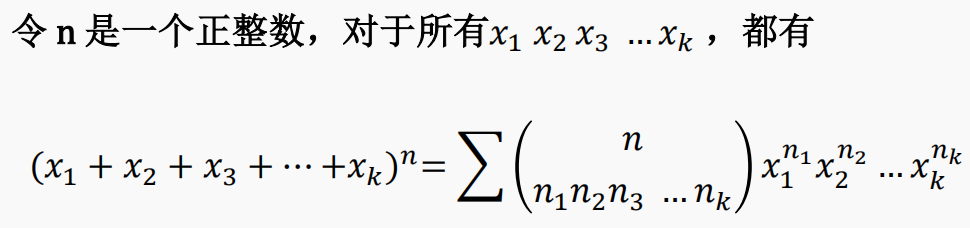
【例】求 $(𝑥1 + 𝑥2 + 𝑥3 + 𝑥4 + 𝑥5)^7$展开时, $𝑥_1^2𝑥_2^3𝑥_4 𝑥_5$的系数
【答案】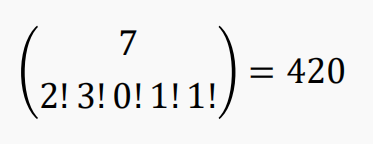
【例】求 $(2𝑥1 − 4𝑥2 + 𝑥3)^7$被展开时, $𝑥_1^2𝑥_2^3𝑥_3^2$ 的系数
【答案】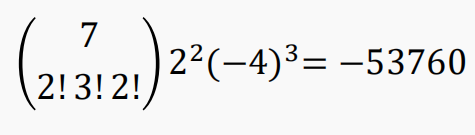
出现在$(𝑥1 + 𝑥2 + 𝑥3 + ⋯ +𝑥𝑘)^𝑛$的多项式展开时中的不同的项的数目等于𝑛1 +𝑛2 +𝑛3 + … +𝑛𝑘= 𝑛
的非负整数解的个数。等于
例题
acwing1307
法一:
1表示公牛,0表示母牛
告诉我们以序列长度为状态,于是设f[i]表示填到第i个位置的方案数,显然第i个位置填0或者1,填0恒满足累加f[i−1],填1导致前k个都不能填0,故累加f[i−k−1],于是有:f[i]=f[i−1]+f[i−k−1]
法二:
dp[i][0]表示前i个数字最后一个数字为0的情况个数,dp[i][1]同理
dp[i][0] = dp[i-1][1]+dp[i-1][0] ,dp[i][1] = dp[i-k-1][1]+dp[i-k-1][0]
法三:
考虑dp[i]表示i位置以1结尾的方案数。转移的时候i前面可以有k只牝牛,或者k+1只,或者k+2只……计算他们的方案数之和即可。用前缀和优化加速。
code
acwing1308
首先呢,g(x)我们是可以求解的,我们设n=g(x)
我们可以先写出n个球,我们发现它们之间有n−1个空隙,而我们的任务是寻找k-1个缝划分成k段,使k段数的和等于n,于是我们就可以将问题转化成在n−1个空隙中选出k−1个空隙放挡板,形成的k段数的和正好就是n。
换句话说,我们要求$C_{n−1}^{k−1}$
code
acwing1309
要在这个棋盘上放 k 个相互不攻击的车,也就是这个车没有两个车在同一行,也没有两个车在同一列,问有多少种方案。
只需要输出答案 mod100003后的结果。

ps:组合数最大开到b+d,空间开两倍
code
acwing1310


ps:δx,δy为P1和P3的横纵坐标之差
P3的方案为什么是(n−δx)(m−δy)?
可将P1映射到原点,P1和P#之间横纵坐标之差为(δx,δy),则P3横坐标的可供选择范围为[δx+1,n],
P3纵坐标的方案数同理。

code
acwing1312
求单调不降不升序列什么的不好做,于是我们给每个数加上它的下标,就转换成了单调下降上升了
这样数列的取值范围变成了[l+1,r+n]
然后我们发现求这样的长度为i的单调上升序列就是在区间中随意取i个数,答案是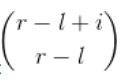
i的范围为1e9,不能直接枚举,采用杨辉三角递推式化简,运用lucas
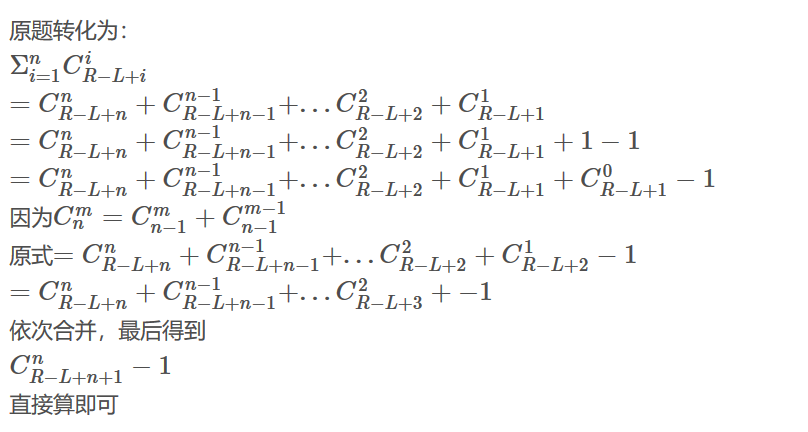
code
hdu5894
一个圆桌上有 n 个不同的位置,m 个相同的人安排到这 n个位置上,要求两个相邻的人至少相距 k 个位置。
求方案数,对1e9+7取模。0 < m < n < 1000000, 0 < k < 1000
样例:(n,m,k) 2
4 2 6
5 2 1
输出:
05
因为一个人坐下之后,后面的 k 个位置一定不能做人。
所以可以把一个人和他旁边的 k 个位置打包看成一个整体。
那么只剩下 n - m(k+1) 个空位。
可以看作 n-m(k+1) 个空位放入 m 个已坐到位置上的人之间。(插空法)
假设计算 n 个球放入 m 个盒子的方案数。
采用隔板法,因为每个盒子里不一定要非空。
答案就是C(n+m-1,m-1)
代入得到答案是C(n-mk-1,m-1)
又因为第一个学生有 n 种选择,还要乘以 n。 m 个盒子是相同的,盒子只要转 m 次可以得到 m 种方案,所以要除以 m。
最后的答案就是 C(n-mk-1,m-1) * n / m
code






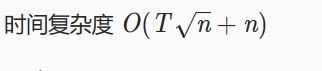
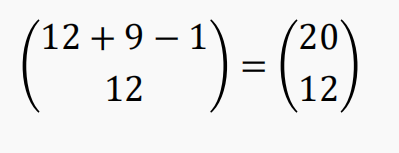
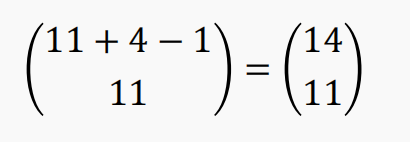
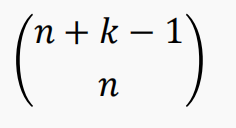

感谢大佬的分享,太棒了!!
一起噶油0v0
mark