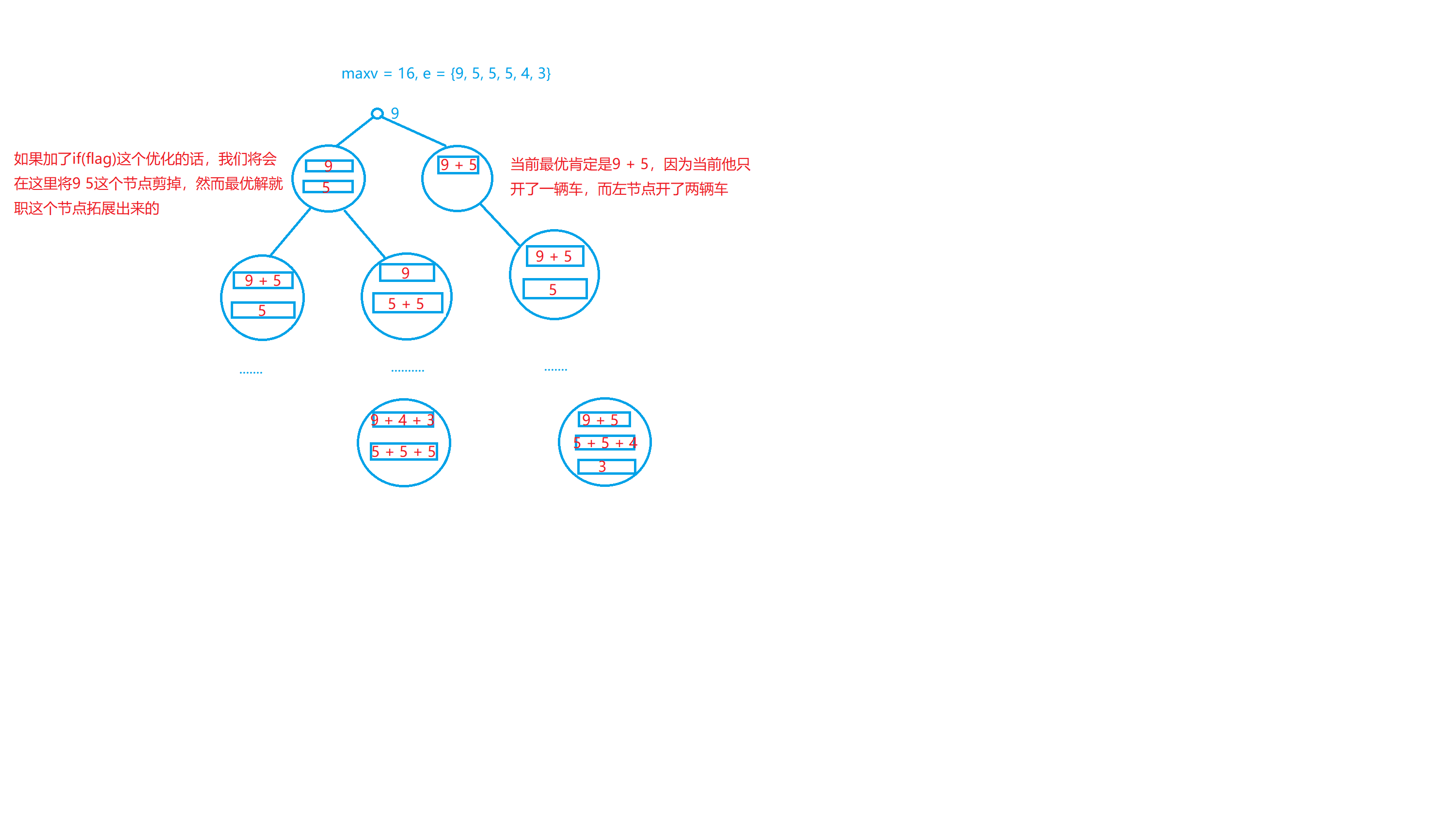
图一
区别: 组是否有容量限制 -> 是否能用flag
- 在小猫爬山的问题中, 局部最优不一定整体最优, 具有后效性
举例说明
在maxV=16时,重量为9 5 5 5 4 3
见图一解释
将当前最优放到新车说不定能装更多的小猫 使得最终状态的车变得少
- 而在分成互质组中, 局部最优一定整体最优
因为它没有容量限制
分成互质组
/*
u -> 第几组
v -> 第几组中的第几个数
w -> n个数我用了多少个数
x -> 当前从哪个序列编号开始找下一个互质的数放入组中
*/
void dfs(int u, int v, int w, int x) // 递归指数型枚举
{
if(u >= res) return ;
if(w == n)
{
res = u;
return ; // 终点时刻要不要这个return都可以
}
/*
20行样例不加flag会T(还是可以跑出正确答案但是要慢6倍左右)
因为不加flag的话在回溯的过程中会多回溯很多次第86行(本来不需要回溯的,
在比较的时候明明可以放到已有的组中却新开组的情况会被淘汰掉63行)
*/
bool flag = 1;
for(int i = x ; i < n ; i ++ )
if(!st[i] && check(u, v, i))
{
group[u][v] = i;
st[i] = 1;
flag = 0;
dfs(u, v + 1, w + 1, i + 1);
/*
在回溯的时候第二种情况会因为上一种情况可以被放到已有的组时(dfs之前)将flag置为0
的条件使得第二条路的判断false, 剪掉了这条分支
*/
st[i] = 0;
}
if(flag) dfs(u + 1, 0, w, 0); // 1. w不变因为我i还没有放进去 2. x == 0因为开辟一个新的组之后我们又从头开始找数了
}
小猫爬山代码
void dfs (int u, int k)
{
if(k >= ans) return ;
if(u == n)
{
ans = k;
return ;
}
// 枚举车
for(int i = 0 ; i < k ; i ++ )
if(sum[i] + m[u] <= w)
{
sum[i] += m[u];
dfs(u + 1, k); // 第一条路
sum[i] -= m[u]; //第二条路 回溯的时候尝试开新车的情况而不是放进已有的车里
}
sum[k] += m[u]; // 注意车是从0开始开的所以k就是一辆新车
dfs(u + 1, k + 1);
sum[k] = 0;
}
int main ()
{
cin >> n >> w;
for(int i = 0 ; i < n ; i ++ ) cin >> m[i];
// *** 优化搜索顺序 先搜索分支小的节点
sort(m, m + n);
reverse(m, m + n);
dfs(0, 0);
cout << ans << endl;
return 0;
}


木棒 这三道题是不同类型的爆搜分组问题 注意一起复习