写在前面,
自己总结的技巧:
1. 优先找到某个空格(其行列与其所在的九宫格能排除最多数的空格)填写利用唯余法
2. 利用区块摒除法, 唯余法填数使得某一九宫格中出现一排填满的数
3. 再利用撑点定位法将并行的三宫尽量填完
4. 当这些方法都不行的时候用候选数法标记
5. 根据数对法, 矩形法求出一些点
6. 发现九宫格中出现某一九宫格中出现一排填满的数再从第1步开始继续做循环往复
7. 最后利用唯一法, 唯一候选数法, 隐性唯一候选数法完成数独
一. 直观法
1. 基础摒除法
一个空格中如果已经确定了, 那么其所在行, 列, 宫都一定没有该数了
注: 这个方法听起来很简单但是是非常好用的
2. 唯一解法
某行或某列或某个九宫格只剩一个空格时, 显然能排除的到其的值
3. 唯余解法
把其行列及其所在的九宫格中已有的1 ~ 9的数字一一踢掉剩下的就是该空格应填的数字
*4. 区块摒除法
1>
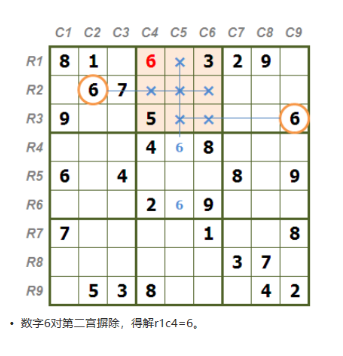
2>

3>
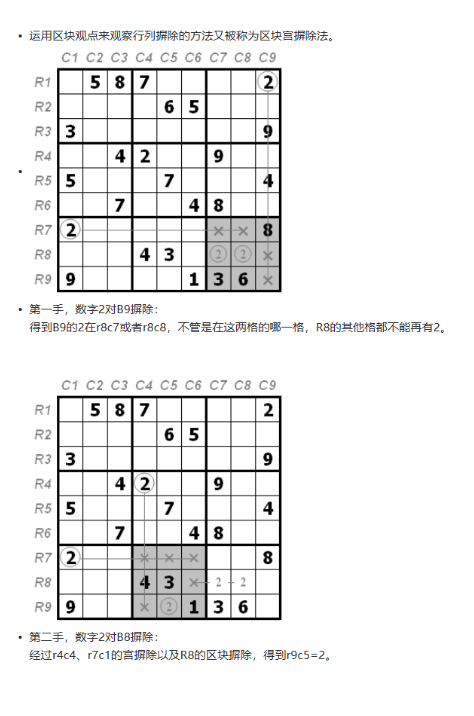
6. 组合摒除法 // 简单可不看 看图理解
如果在横向并行的两个九宫格中,某个数字可能填入的位置正好都分别占据相同的两行,则这两行可以被用来对横向并行的另一九宫格做行摒除。
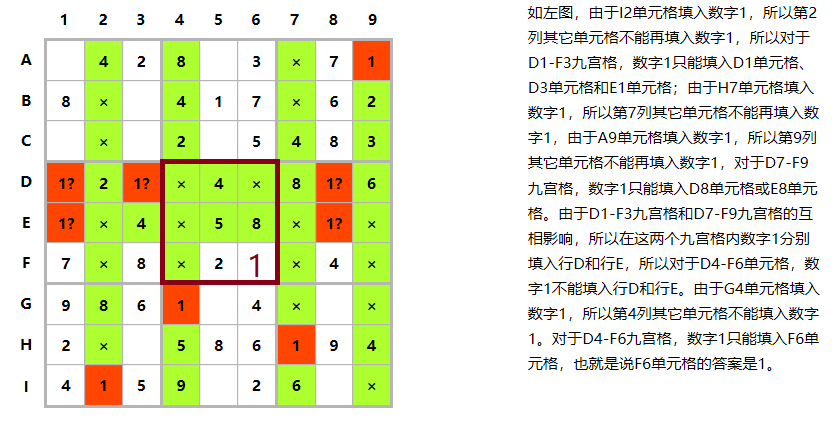
如果在纵向并列的两个九宫格中,某个数字可能填入的位置正好都分别占据相同的两列,则这两列可以被用来对纵向并行的另一九宫格做列摒除。

*7. 撑点定位法

8. 尝试法
在某行或列,九宫格所填数字比较多,剩余2个或3个时,在剩余宫格添入值尝试添入数是否成立,
值得注意的是当只剩两个空时, 如果有5, 6两种选择, 则我们一定要将两个数都代入检测, 一个成立, 一个不成立,
才能说明我们的成立的猜测是正确的
二. 候选数法(见参考资料)
写在前面,
隐形就是扣自己(扣成特征形式), 显性就是扣别人
1. 唯一候选数法
唯一候选数法是候选数删减法中最简单的一种方法,就是通览所有单元格的候选数列表,如果哪个单元格中只剩下一个候选数,就可应用唯一候选数法,在该单元格中填入这个数字,并在相应行,列和九宫格的其它单元格候选数列表中删除该数字
2. 隐式唯一候选数法
由于1-9这9个数字要在每行、每列和每个九宫格内至少出现一次,所以如果某个数字在某行、某列或是某个九宫格内所有单元格的候选数列表中只出现一次,那么这个数字就应该填入它出现的那个单元格内,并且从该格所在行、所在列和所在九宫格内其它单元格的候选数列表中删除该数字。
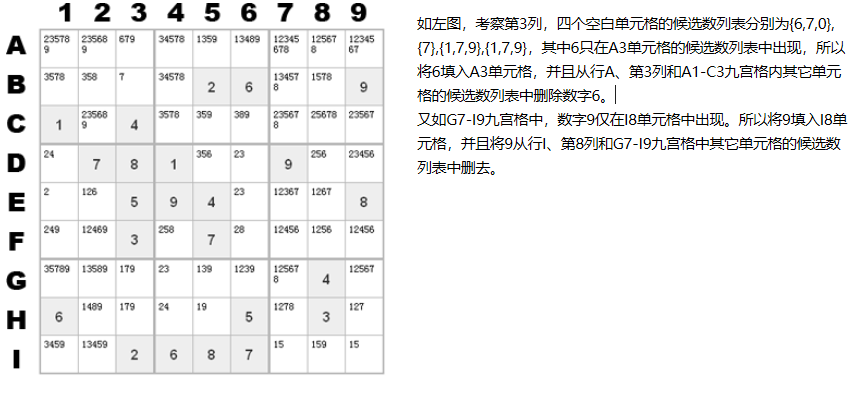
3. 候选数区块删减法
在某一九宫格中,当所有可能出现某个数字的单元格都位于同一行时,就可以把这个数字从该行的其他单元格的候选数中删除;
在某一九宫格中,当所有可能出现某个数字的单元格都位于同一列时,就可以把这个数字从该列的其他单元格的候选数中删除;
在某一行(列)中,当所有可能出现某个数字的单元格都位于同一九宫格中时,就可以把这个数字从该九宫格的其他单元格的候选数中删除。
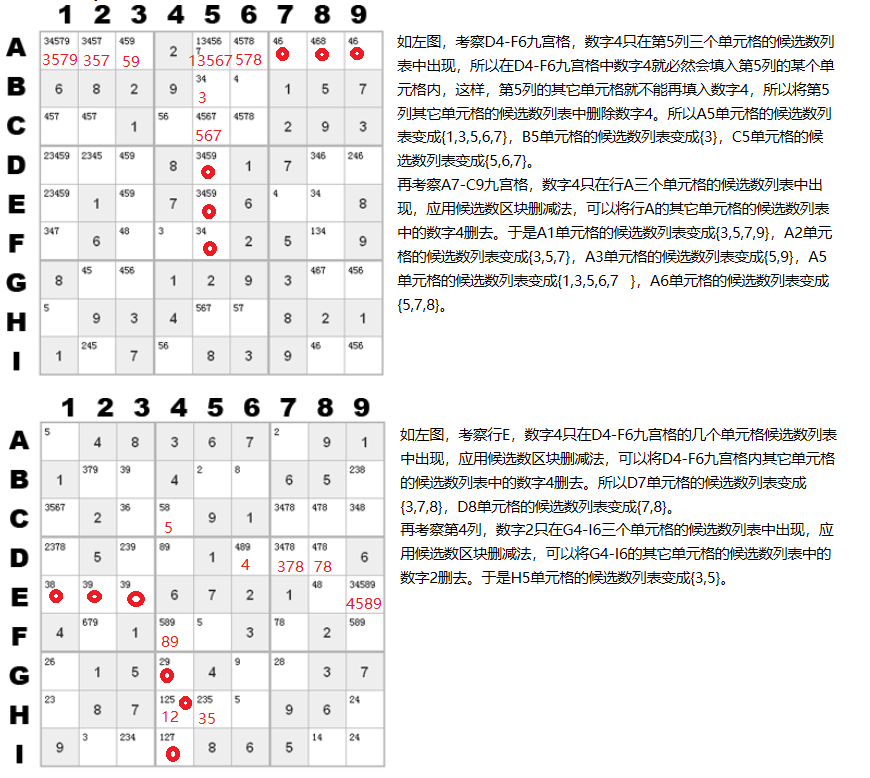
4. 候选数对删减法
候选数对删减法依据的原理是数字1-9在同一行、同一列和同一九宫格内不能出现2次或2次以上。这样,如果在同一行、同一列和同一九宫格内两个单元格的候选数列表都是{a,b},那么如果其中一个单元格填入的数字为a,另一个单元格填入的数字就应该是b;反之,如果其中一个单元格填入的数字为b,另一个单元格填入的数字就应该是a。也就是说,a,b两个数字就应该分别填入这两个单元格,所以该行、该列或是该九宫格内其它单元格就不应该再填入数字a和b。
所以候选数对删减法就是:在一个行、列或九宫格中,如果有两个单元格都包含且只包含相同的两个候选数,则这两个候选数字应该从该行、该列列或该九宫格的其他单元格的候选数列表中删去。

5. 隐式候选数对删减法
隐性候选数对删减法依据的原理是数字1-9在同一行、同一列和同一九宫格内至少要出现一次。这样,如果某两个数字a和b在同一行、同一列和同一九宫格内只在两个单元格的候选数列表中出现,那么该行、该列或是该九宫格内其它单元格就不应该再填入数字a和b,所以a和b只能在这两个单元格中出现,所以这两个单元格的候选数列表就都应该是{a,b},可以将其他的数字从这两个单元格的候选数列表中删去
所以隐性候选数对删减法就是:在同一行,列或区块中,如果一个数对(两个数字)正好只出现且都出现在两个单元格中,则这两个单元格的候选数中的其他数字可以被删除。
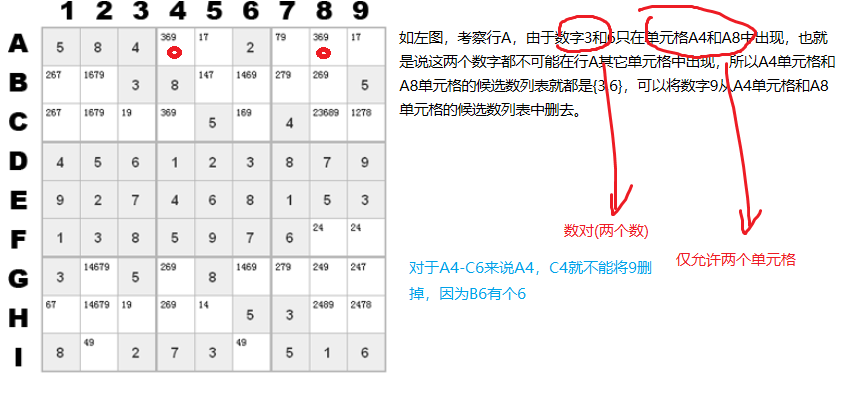
6. 三数集删减法
三数集删减法的原理类似于候选数对删减法。候选数对删减法要求同样的2个数字都出现在某行、列或九宫格的2个单元格中,且这2个单元格的候选数不能包含其他的数字。同样,三数集删减法要求的是3个数字要出现在3个位于同一行、列或九宫格的单元格中,且这3个单元格的候选数中不能包含其他数字。但不同的是,三数集删减法不要求每个单元格中都要包含这3个数字。例如,对于数字集{2,4,5},如果在某行,列或区块中有3个单元格的候选数分别为下面几种情况时,都可应用三数集删减法:
{2, 4, 5}、{2, 4, 5}、{2, 4, 5};
{2, 4}、{4, 5}、{2, 5};
{2, 4, 5}、{2, 5}、{4, 5};
{2, 4, 5}、{4, 5}、{2, 4, 5};
……
也就是说,要形成三数集,则必须要有3个在同一行、列或九宫格中的单元格,每个单元格中至少要有2个候选数,且它们的所有候选数字也正好都是一个三数集的子集。这个三数集中的3个数字只能填入这3个单元格中,所以该行、列或九宫格中其他的单元格中不可能再填入这3个数字。
但要注意的是,{2, 4, 5}、{2, 4}、{2, 4}这种情况不是三数集。其中{2, 4}和
{2, 4}可应用候选数对删减法,所以第一个候选数列表{2, 4, 5}将只能剩下候选数5,这时就可应用唯一候选数法了

7. 隐性三数集删减法
隐性三数集删减法相对于三数集删减法就类似于隐形候选数对删减法相对于候选数对删减法。当某个3个数字只出现在某行、列或九宫格的3个单元格中,且每个单元格中至少包含有其中的2个数字时,则可以把其他数字从这3个单元格的候选数中删除。
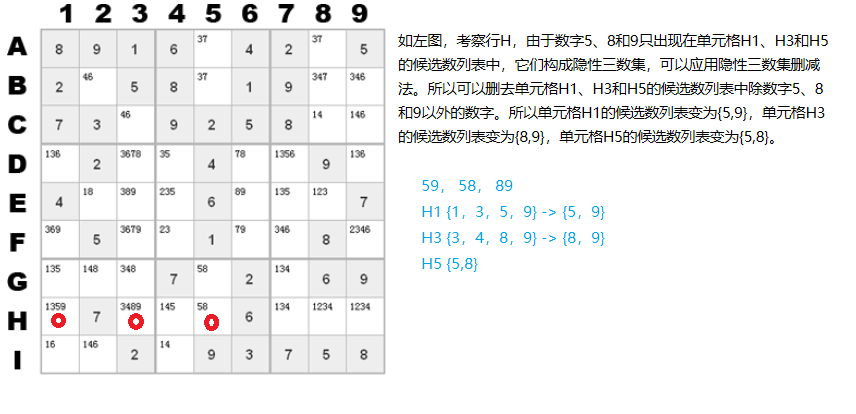
8. 三链数删减法
三链数删减法类似于矩形删减法,是矩形删减法的推广。三链数删减法指的是如果某个数字在某三列中只出现在相同的三行中,则这个数字将从这三行上其他的候选数中删除;或者如果某个数字在某三行中只出现在相同的三列中,则这个数字也将从这三列上其他的候选数中删除。
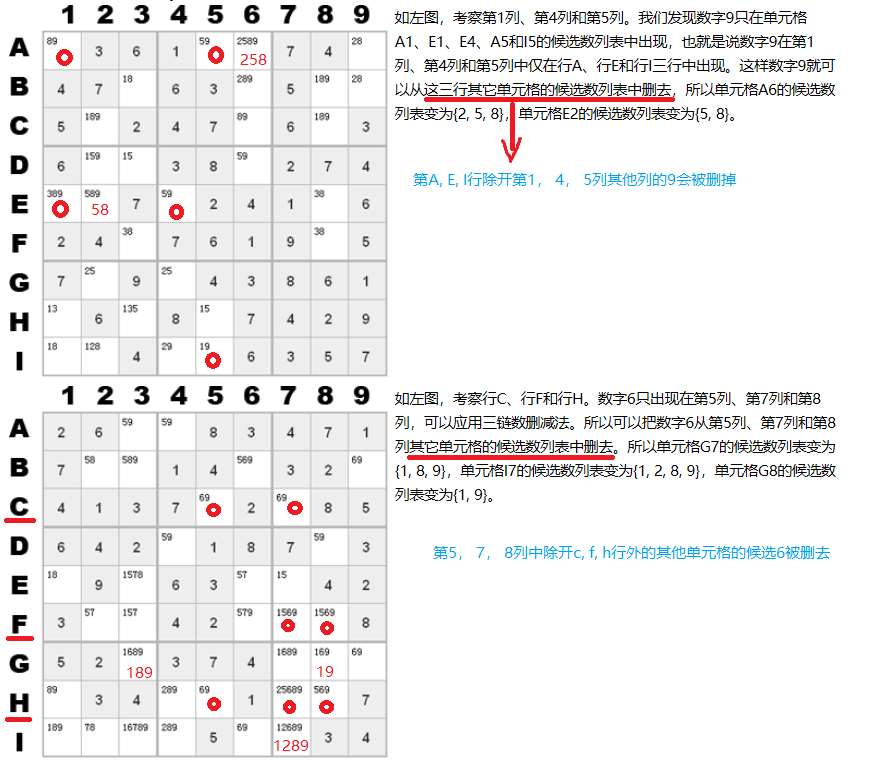
9. 矩形顶点法 -> 不适用于九宫格
候选数矩形删减法类似于直观法中的矩形摒除法。
如果一个数字正好出现且只出现在某两行的相同的两列上,则这个数字就可以从这两列上其他的单元格的候选数中删除;
如果一个数字正好出现且只出现在某两列的相同的两行上,则这个数字就可以从这两行上的其他单元格的候选数中删除

// 以下三种方法见参考资料
10. XY形态匹配删减法
11. XYZ形态匹配删减法
12. WXYZ形态匹配删减法
数独是一个很锻炼数学思维的游戏, 大家没事可以多玩玩哦~

