来自算法基础课

树和图的存储(有向图，如果是无向图就存储两条有向边即可)

1.邻接表(适合于稀疏图)

const int N = 100005;

int h[N], e[N * 2], w[N * 2], ne[N * 2], idx;

memset(h, -1, sizeof(h));

void add(int a, int b, int c){
    e[idx] = b;
    w[idx] = c;
    ne[idx] = h[a];
    h[a] = idx;
    idx ++;
}

2.邻接矩阵(适合于稠密图)

const int N = 1005;

int g[N][N];

memset(g, 0x3f, sizeof(g));

void add(int a, int b, int c){
    g[a][b] = min(g[a][b], c);
}

树和图的深度优先搜索 $O(m)$

const int N = 100005;

int h[N], e[N * 2], ne[N * 2], idx;
bool st[N];

void dfs(int u){
    st[u] = true;
    for(int i = h[u]; i != -1; i = ne[i]){
        int j = e[i];
        if(!st[j]){
            // 具体问题的逻辑

            dfs(j);
        }
    }
}

树和图的广度优先遍历 $O(m)$

const int N = 100005;

int h[N], e[N * 2], ne[N * 2], idx;
bool st[N];

void bfs(){
    memset(st, false, sizeof(st));
    st[1] = true;
    queue<int> q;
    q.push(1);
    while(!q.empty()){
        int u = q.front();
        q.pop();
        for(int i = h[u]; i != -1; i = ne[i]){
            int j = e[i];
            if(st[j] == false){
                // 具体问题的逻辑

                st[j] = true;
                q.push(j);
            }
        }
    }
}

topsort(拓扑排序) $O(m)$

const int N = 100005;

int e[N], ne[N], h[N], idx;
int q[N], hh = 0, tt = -1;
int d[N];

void add(int a, int b){
    e[idx] = b;
    ne[idx] = h[a];
    h[a] = idx;
    idx ++;
    d[b] ++;
}

void print(bool is_ok){
    if(is_ok == false)
        puts("impossible");
    else{
        for(int i = 0; i < n - 1; i ++)
            printf("%d ", q[i]);
        putchar('\n');
    }
}

void topsort(){
    for(int i = 1; i <= n; i ++)
        if(d[i] == 0)
            q[++ tt] = i;
    while(hh <= tt){
        int t = q[hh ++];
        for(int i = h[t]; i != -1; i = ne[i]){
            int j = e[i];
            d[j] --;
            if(d[j] == 0)
                q[++ tt] = j;
        }
    }
    print(tt == n - 1);
}

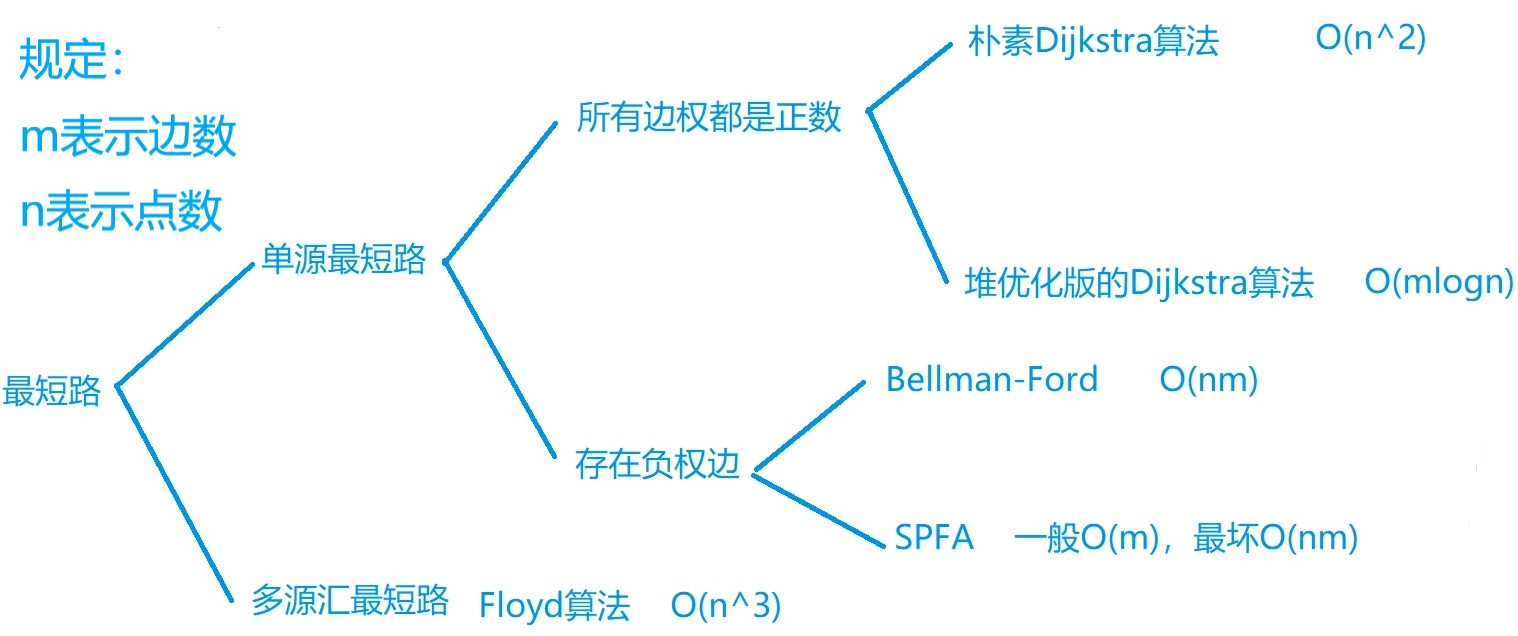
朴素版Dijkstra算法 $O(n ^ 2)$

/*
Dijkstra算法：
    1.dist[1] = 0, dist[i] = ∞(i = 2~n)
    2.循环n次
        t<-不在集合中的距离最近的点
        将t加入S
        用t更新其他点的距离
    3.if dist[n] > 0x3f3f3f3f
        就说明不存在最短路
      else
        dist[n]就是1~n的最短路 
*/

#include<bits/stdc++.h>
using namespace std;

const int N = 505;

int g[N][N], dist[N], st[N];
int n, m;

int dijkstra(){
    memset(dist, 0x3f, sizeof(dist));
    dist[1] = 0;
    for(int i = 1; i <= n; i ++){
        int t = -1;
        for(int j = 1; j <= n; j ++)
            if(!st[j] && (t == -1 || dist[t] > dist[j]))
                t = j;
        st[t] = true;
        for(int j = 1; j <= n; j ++)
            dist[j] = min(dist[j], dist[t] + g[t][j]);
    }
    if(dist[n] == 0x3f3f3f3f)
        return -1;
    else
        return dist[n];
}

int main(){
    scanf("%d %d", &n, &m);
    memset(g, 0x3f, sizeof(g));
    while(m --){
        int a, b, c;
        scanf("%d %d %d", &a, &b, &c);
        g[a][b] = min(g[a][b], c);
    }
    printf("%d\n", dijkstra());
    return 0;
}

堆优化版Dijkstra算法 $O(mlog(m))$

/*
堆优化Dijkstra算法：
    1.dist[1] = 0, dist[i] = ∞(i = 2~n)
    2.heap：(0，1)
    3.while heap不空 
        t<-堆顶元素 
        将t加入S
        for t的所有出边a->b
            如果可以更新1->b的距离 
                将b加入heap
    4.if dist[n] > 0x3f3f3f3f
        就说明不存在最短路
      else
        dist[n]就是1~n的最短路 
*/

#include<bits/stdc++.h>
using namespace std;

typedef pair<int, int> PII;

const int N = 100005;

int h[N], e[N], w[N], ne[N], idx;
int dist[N], st[N];
int n, m;

void add(int a, int b, int c){
    e[idx] = b;
    w[idx] = c;
    ne[idx] = h[a];
    h[a] = idx;
    idx ++;
}

int dijkstra(){
    memset(st, false, sizeof(st));
    memset(dist, 0x3f, sizeof(dist));
    dist[1] = 0;
    priority_queue<PII, vector<PII>, greater<PII> > q;
    q.push(make_pair(0, 1));
    while(!q.empty()){
        PII t = q.top();
        q.pop();
        int ver = t.second, distance = t.first;
        if(st[ver])
            continue;
        st[ver] = true;
        for(int i = h[ver]; i != -1; i = ne[i]){
            int j = e[i];
            if(dist[j] > distance + w[i]){
                dist[j] = distance + w[i];
                q.push(make_pair(dist[j], j));
            }
        }
    }
    return (dist[n] == 0x3f3f3f3f ? -1 : dist[n]);
}

int main(){
    memset(h, -1, sizeof(h));
    scanf("%d %d", &n, &m);
    while(m --){
        int a, b, c;
        scanf("%d %d %d", &a, &b, &c);
        add(a, b, c);
    }
    printf("%d\n", dijkstra());
    return 0;
}

Bellman_ford算法 $O(n * m)$

/*
Bellman_ford算法：  
    1.dist[1] = 0, dist[i] = ∞(i = 2~n)
    2.循环k次
        backup = dist
        循环所有边a->b, 权重为w
            如果dist[b]可以被更新
                更新dist[b]
    3.if dist[n] > 0x3f3f3f3f / 2
        不存在最短路
      else
        dist[n]就是1~n的最短路
*/

#include<bits/stdc++.h>
using namespace std;

const int N = 505, M = 10005;

int dist[N], backup[N];
int n, m, k;

struct Edge{
    int a, b, w;
}edges[M];

int bellman_ford(){
    memset(dist, 0x3f, sizeof(dist));
    dist[1] = 0;
    for(int i = 0; i < k; i ++){
        memcpy(backup, dist, sizeof(dist));
        for(int j = 0; j < m; j ++){
            int a = edges[j].a, b = edges[j].b, w = edges[j].w;
            dist[b] = min(dist[b], backup[a] + w);
        }
    }
    return (dist[n] > 0x3f3f3f3f / 2 ? 0x3f3f3f3f : dist[n]);
}

int main(){
    scanf("%d %d %d", &n, &m, &k);
    for(int i = 0; i < m; i ++){
        int a, b, w;
        scanf("%d %d %d", &a, &b, &w);
        edges[i] = {a, b, w};
    }
    int t = bellman_ford();
    if(t == 0x3f3f3f3f)
        puts("impossible");
    else
        printf("%d\n", dist[n]);
    return 0;
}

Spfa算法 $平均为O(km), 最坏O(n * m)$

/*
Spfa算法：
    1.dist[1] = 0, dist[i] = ∞(i = 2~n)
    2.queue：1
    3.while queue不空
        t<-queue.front()
        更新t的所有出边a->b, 权重为w
            将b加入queue
    4.if dist[n] = ∞
        就说明不存在最短路
      else
        dist[n]就是1~n的最短路
*/

#include<bits/stdc++.h>
using namespace std;

const int N = 100005;

int h[N], e[N], ne[N], w[N], idx;
int dist[N], st[N];
int n, m;

void add(int a, int b, int c){
    e[idx] = b;
    ne[idx] = h[a];
    h[a] = idx;
    w[idx] = c;
    idx ++;
}

int spfa(){
    memset(dist, 0x3f, sizeof(dist));
    dist[1] = 0;
    queue<int> q;
    q.push(1);
    st[1] = true;
    while(!q.empty()){
        int u = q.front();
        q.pop();
        st[u] = false;
        for(int i = h[u]; i != -1; i = ne[i]){
            int j = e[i];
            if(dist[j] > dist[u] + w[i]){
                dist[j] = dist[u] + w[i];
                if(!st[j]){
                    q.push(j);
                    st[j] = true;
                }
            }
        }
    }
    return dist[n];
}

int main(){
    memset(h, -1, sizeof(h));
    scanf("%d %d", &n, &m);
    while(m --){
        int a, b, w;
        scanf("%d %d %d", &a, &b, &w);
        add(a, b, w);
    }
    int t = spfa();
    if(t == 0x3f3f3f3f)
        puts("impossible");
    else
        printf("%d\n", t);
    return 0;
}

用Spfa判断负环 $平均为O(km), 最坏O(n * m)$

/*
Spfa判断负环算法：
    1.dist[1] = 0, dist[i] = ∞(i = 2~n)
    2.queue：1
    3.while queue不空
        t<-queue.front()
        更新t的所有出边a->b, 权重为w
            将b加入queue
        if 存在一个j使得从1到j的最短路长度>=n
            就说明有负环
    4.如果最后不存在一个j使得从1到j的最短路长度>=n
        就说明没有负环
*/

#include<bits/stdc++.h>
using namespace std;

const int N = 2005, M = 10005;

int h[N], w[M], e[M], ne[M], idx;
int dist[N], cnt[N];
bool st[N];
int n, m;

void add(int a, int b, int c){
    w[idx] = c;
    e[idx] = b;
    ne[idx] = h[a];
    h[a] = idx;
    idx ++;
}

bool spfa(){
    memset(dist, 0x3f, sizeof(dist));
    dist[1] = 0;
    queue<int> q;
    for(int i = 1; i <= n; i ++){
        q.push(i);
        st[i] = true;
    }
    while(!q.empty()){
        int u = q.front();
        q.pop();
        st[u] = false;
        for(int i = h[u]; i != -1; i = ne[i]){
            int j = e[i];
            if(dist[j] > dist[u] + w[i]){
                dist[j] = dist[u] + w[i];
                cnt[j] = cnt[u] + 1;
                if(!st[j]){
                    q.push(j);
                    st[j] = true;
                }
                if(cnt[j] >= n)
                    return true;
            }
        }
    }
    return false;
}

int main(){
    memset(h, -1, sizeof(h));
    scanf("%d %d", &n, &m);
    while(m --){
        int a, b, c;
        scanf("%d %d %d", &a, &b, &c);
        add(a, b, c);
    }
    if(spfa())
        puts("Yes");
    else
        puts("No");
    return 0;
}

Floyd算法 $O(n ^ 3)$

/*
Floyd算法：基于动态规划
    1.d[i][j]为i->j边的权重（若无，则为∞）
    2.for(int k = 1; k <= n; k ++)
        for(int i = 1; i <= n; i ++)
            for(int j = 1; j <= n; j ++)
                从i到j的距离更新成i到k的距离加上k到j的距离
    3.if dist[n] > 0x3f3f3f3f / 2
        就说明不存在最短路
      else
        dist[n]就是1~n的最短路 
*/

#include<bits/stdc++.h>
using namespace std;

const int N = 205, INF = 0x3f3f3f3f;

int d[N][N];
int n, m, Q;

void floyd(){
    for(int k = 1; k <= n; k ++)
        for(int i = 1; i <= n; i ++)
            for(int j = 1; j <= n; j ++)
                d[i][j] = min(d[i][j], d[i][k] + d[k][j]);
}

int main(){
    scanf("%d %d %d", &n, &m, &Q);
    memset(d, 0x3f, sizeof(d));
    for(int i = 1; i <= n; i ++)
        d[i][i] = 0;
    while(m --){
        int a, b, c;
        scanf("%d %d %d", &a, &b, &c);
        d[a][b] = min(d[a][b], c);
    }
    floyd();
    while(Q --){
        int a, b;
        scanf("%d %d", &a, &b);
        if(d[a][b] >= INF / 2)
            puts("impossible");
        else
            printf("%d\n", d[a][b]);
    }
    return 0;
}

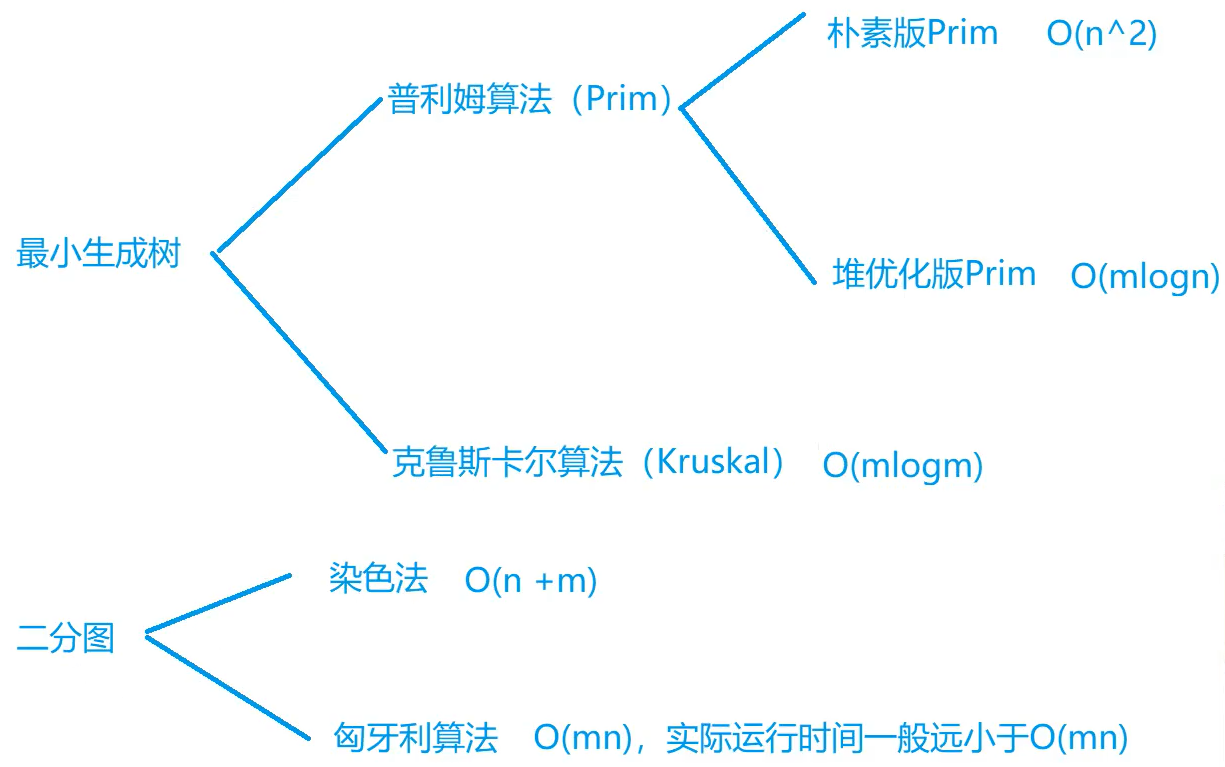
朴素版Prim算法 $O(n ^ 2)$

/*
Prim算法：
    1.dist[i] = ∞
    2.循环n次
        t<-集合外离集合最近的点
        用t更新其他所有点到集合的距离
        t加入集合
*/

#include<bits/stdc++.h>
using namespace std;

const int N = 505, INF = 0x3f3f3f3f;

int g[N][N], dist[N];
bool st[N];
int n, m;

int prim(){
    int res = 0;
    memset(dist, 0x3f, sizeof(dist));
    for(int i = 0; i < n; i ++){
        int t = -1;
        for(int j = 1; j <= n; j ++)
            if(!st[j] && (t == -1 || dist[t] > dist[j]))
                t = j;
        if(i && dist[t] == INF)
            return INF;
        if(i)
            res += dist[t];
        for(int j = 1; j <= n; j ++)
            dist[j] = min(dist[j], g[t][j]);
        st[t] = true;
    }
    return res;
}

int main(){
    memset(g, 0x3f, sizeof(g));
    scanf("%d %d", &n, &m);
    while(m --){
        int a, b, c;
        scanf("%d %d %d", &a, &b, &c);
        g[a][b] = min(g[a][b], c);
        g[b][a] = min(g[b][a], c);
    }
    int t = prim();
    if(t == INF)
        puts("impossible");
    else
        printf("%d\n", t);
    return 0;
}

Kruskal算法 $O(mlog(m))$

/*
Kruskal算法：O(mlog(m))
    1.将所有遍按从小到大排序（这是Kruskal算法的瓶颈） O(mlog(m))
    2.枚举每条边a-b，权重是w O(m)
        if a,b不在一个集合之中
            就将这条边加入集合（cnt ++，res += w）
    3.if cnt < n-1
        就说明图是不连通的
      else 
        res存的就是最小生成树的树边权重之和
    因为要合并集合，所以要用并查集维护
*/

#include<bits/stdc++.h>
using namespace std;

const int N = 200005;

int p[N];
int n, m, res = 0, cnt = 0;

struct Edge{
    int a, b, w;
    bool operator< (const Edge& W)const{
        return w < W.w;
    }
}edges[N];

int find(int x){
    if(p[x] != x)
        p[x] = find(p[x]);
    return p[x];
}

void kruskal(){
    for(int i = 1; i <= n; i ++)
        p[i] = i;
    sort(edges, edges + m);
    for(int i = 0; i < m; i ++){
        int a = edges[i].a, b = edges[i].b, w = edges[i].w;
        int A = find(a), B = find(b);
        if(A != B){
            p[A] = B;
            res += w;
            cnt ++;
        }
    }
}

int main(){
    scanf("%d %d", &n, &m);
    for(int i = 0; i < m; i ++){
        int a, b, w;
        scanf("%d %d %d", &a, &b, &w);
        edges[i] = {a, b, w};
    }
    kruskal();
    if(cnt < n - 1)
        puts("impossible");
    else
        printf("%d\n", res);
    return 0;
}

染色法判断二分图 $O(n + m)$

/*
染色法：
    1.color[] = 0; 0表示没有染色，1表示染黑色，2表示染白色
    2.dfs(u, c) 表示第u个点染颜色c是否行
        (1)color[u] = c
        (2)for u的所有出边u->j
            1°.if j这个点没有染色
                if dfs(j, 3 - c)不成立
                    return false
            2°.if color[j]和c相等
                return false
    3.for i = 1~n
        if 这个点没有染色
            if dfs(i, 1)不成立
                就说明这个图不是二分图
    else 就说明这个图是二分图
*/

#include<bits/stdc++.h>
using namespace std;

const int N = 100005;

int h[N], e[2 * N], ne[2 * N], idx;
int color[N];
int n, m;

void add(int a, int b){
    e[idx] = b;
    ne[idx] = h[a];
    h[a] = idx;
    idx ++;
}

bool dfs(int u, int c){
    color[u] = c;
    for(int i = h[u]; i != -1; i = ne[i]){
        int j = e[i];
        if(!color[j]){
            if(!dfs(j, 3 - c))
                return false;
        }
        else if(color[j] == c)
            return false;
    }
    return true;
}

int main(){
    memset(h, -1, sizeof(h));
    scanf("%d %d", &n, &m);
    while(m --){
        int a, b;
        scanf("%d %d", &a, &b);
        add(a, b), add(b, a);
    }
    bool flag = true;
    for(int i = 1; i <= n; i ++)
        if(!color[i])
            if(!dfs(i, 1)){
                flag = false;
                break;
            }
    if(!flag)
        puts("No");
    else
        puts("Yes");
    return 0;
}

二分图的最大匹配(匈牙利算法) $理论时间O(nm)，实际运行时间远低于此值$

#include<bits/stdc++.h>
using namespace std;

const int N = 505, M = 100005;

int h[N], e[M], ne[M], idx;
int match[N];
bool st[N];
int n1, n2, m;

void add(int a, int b){
    e[idx] = b;
    ne[idx] = h[a];
    h[a] = idx;
    idx ++;
}

bool find(int x){
    for(int i = h[x]; i != -1; i = ne[i]){
        int j = e[i];
        if(!st[j]){
            st[j] = true;
            if(match[j] == 0 || find(match[j])){
                match[j] = x;
                return true;
            }
        }
    }
    return false;
}

int xiongyali(){
    int res = 0;
    for(int i = 1; i <= n1; i ++){
        memset(st, false, sizeof(st));
        if(find(i))
            res ++;
    }
    return res;
}

int main(){
    memset(h, -1, sizeof(h));
    scanf("%d %d %d", &n1, &n2, &m);
    while(m --){
        int a, b;
        scanf("%d %d", &a, &b);
        add(a, b);
    }
    int t = xiongyali();
    printf("%d\n", t);
    return 0;
}