卡特兰数

棋盘问题：n行n列的棋盘，从左下角走到右上角，一直在对角线下面走,不穿过对角线，有多少种走法？

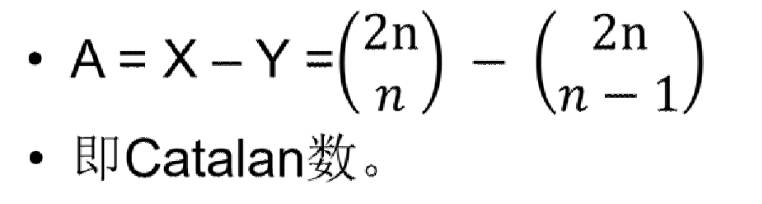
卡塔兰数的一般项公式为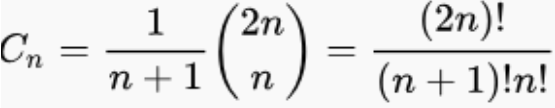
前10项为：1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862，n=0,1,2....

另一个表达形式：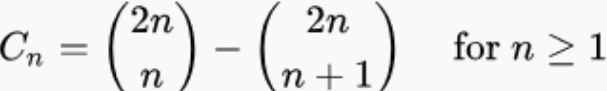

递推关系（计算复杂度 O(n2)）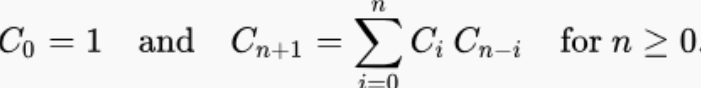

递推关系（计算复杂度 O(n)）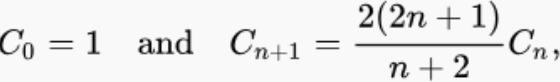

Catalan 数的组合学意义
（1）从（0，0）点沿第一象限的格线到（n，n）点的不穿越方格对角线的最短路径数。

（2）用 n-1 条互不交叉的对角线把 n+2 条边（n≥1）的凸多边形拆分三角形化的方法数。

（3）甲乙两人比赛乒乓球，最后结果为 n:n，比赛过程中甲始终不落后于乙的计分种数。

（4）n 个点的有序二叉树的个数

（5）n 个叶子的完全二叉树的个数

（6）圆周上 2n 个点连成的 n 条两两互不相交的弦分割圆的方案数。

模板题

#include<iostream>
#include<algorithm>
using namespace std;
const int mod=1e9+7;
typedef long long LL;

int qmi(int a,int k,int p)
{
    int res=1;
    while(k)
    {
        if(k&1)
            res=(LL)res*a%mod;
        a=(LL)a*a%mod;
        k>>=1;
    }
    return res;
}

int main()
{
    int n;
    cin>>n;

    int res=1;
    for(int i=2*n,j=1;j<=n;i--,j++)
    {
        res=(LL)res*i%mod;
        res=(LL)res*qmi(j,mod-2,mod)%mod;
    }

    res=(LL)res*qmi(n+1,mod-2,mod)%mod;

    cout<<res<<endl;
    return 0;
}

acwing1135


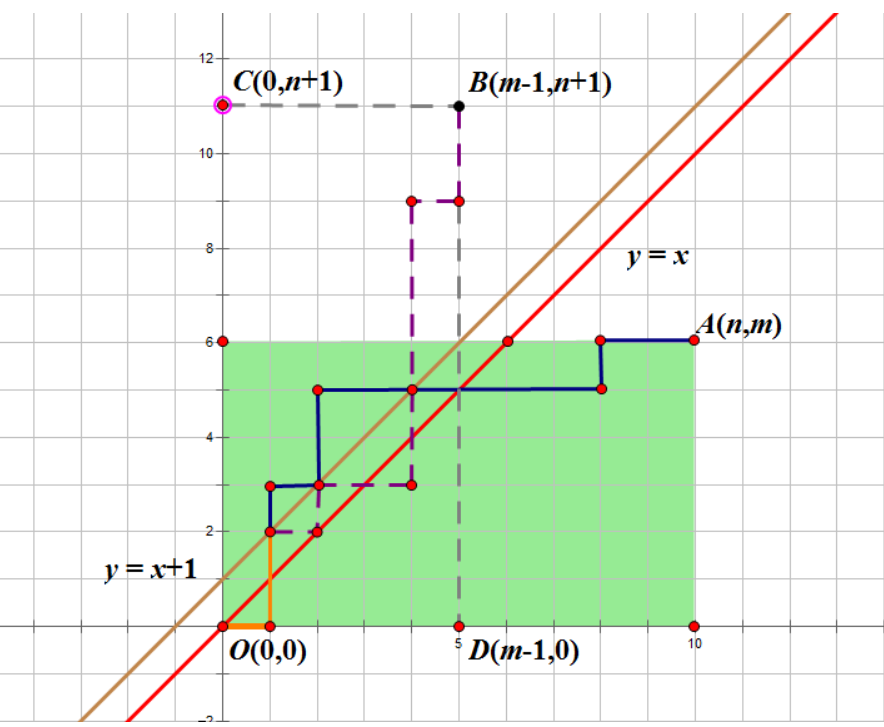
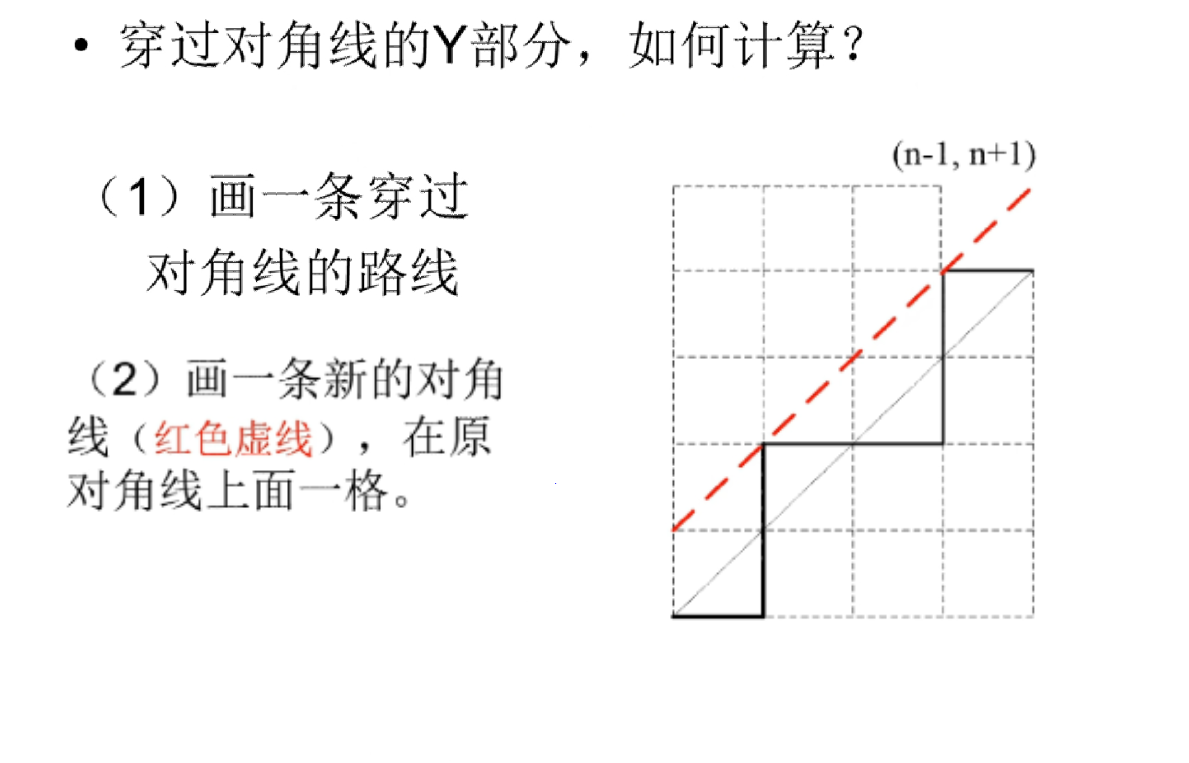
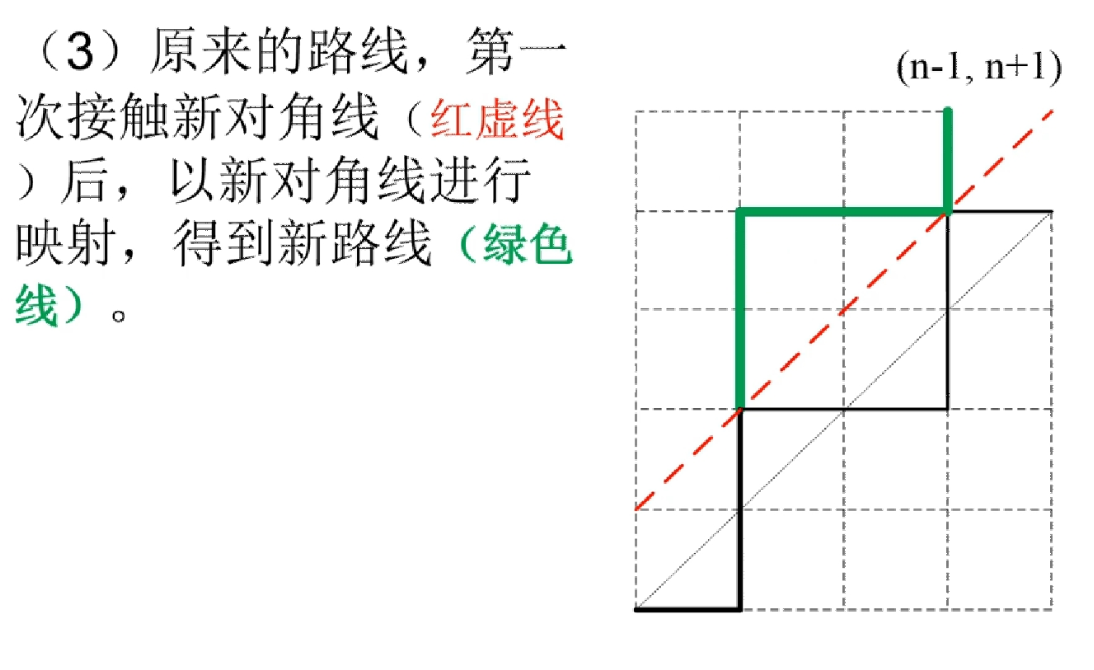
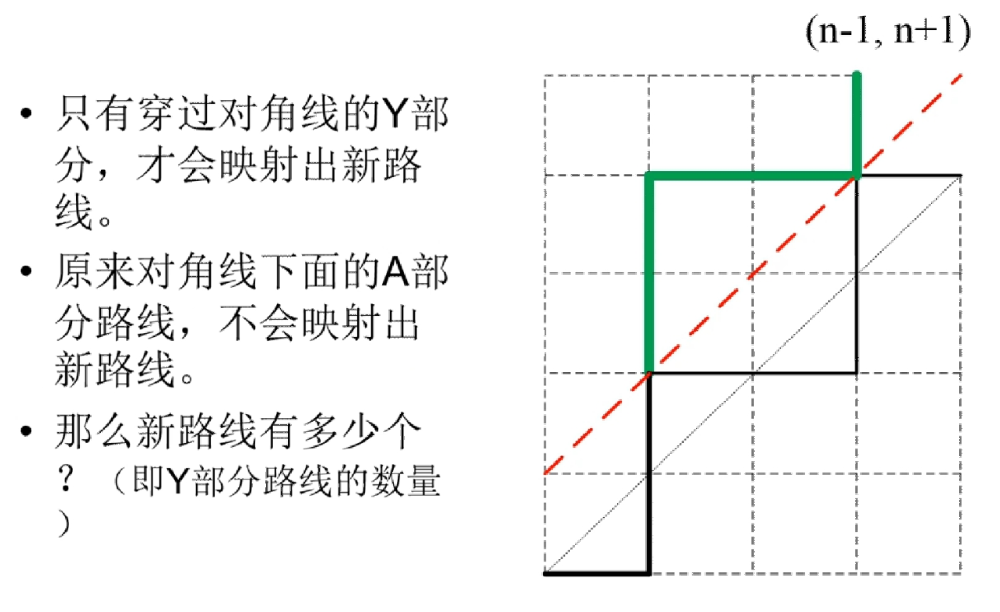
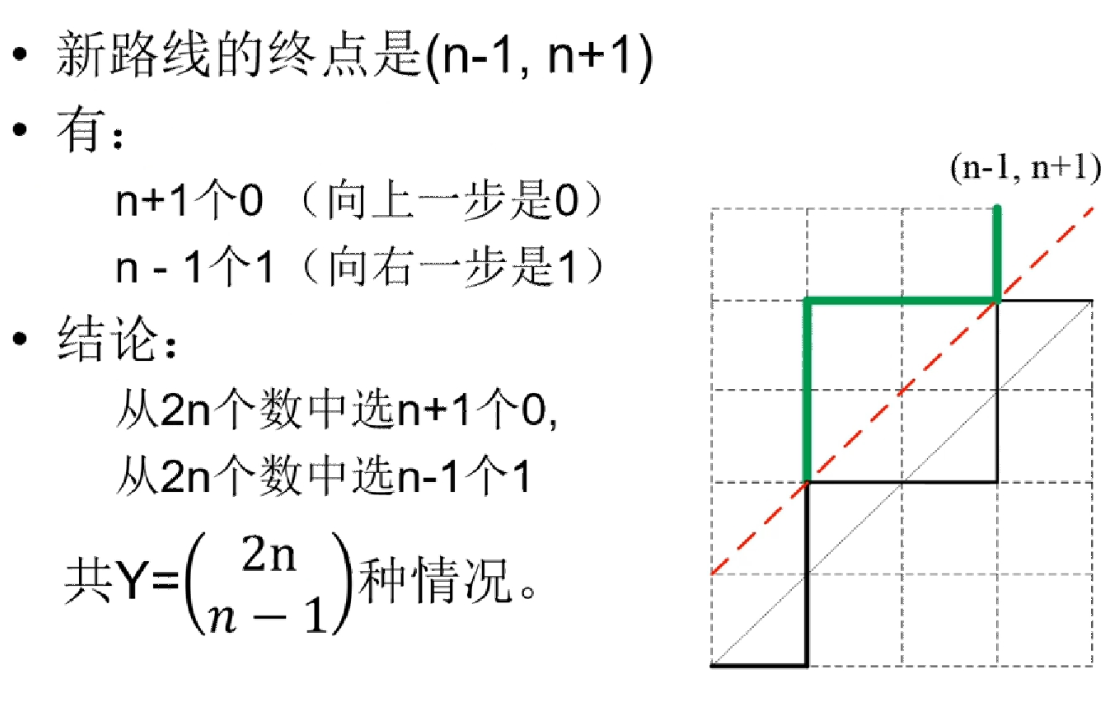
易得，不能穿过y=x这条直线就等于不能碰到y=x+1，所以我们找到y=x+1这条直线（图中为棕色直线），并将原路径沿这条直线对称过去（除了最下面的一段，图中为橙色）

code

acwing1316

我们把奇数和偶数位置上的数分别拿出来形成两个数列，那么要求就是这两个数列均为单调递增的并且偶数数列在对应位置上大于奇数数列。那么我们就从小到大往两个数列里填数，那么只要在对应位置上奇数数列先填数，偶数数列后填数即可得到一个满足题意的情况。而换句话说，就是必须奇数数列的该位置有数了，偶数数列的该位置才可能被填。那么我们把这个与卡特兰数经典的括号匹配问题做一个类比，在奇数数列填数就相当于在括号序列末尾加一个左括号，在偶数数列填数就相当于在括号末尾加一个右括号，所以这题的答案也是卡特兰数。
code

高斯消元

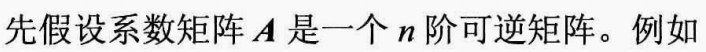
#include<iostream>
#include<cstring>
#include<cstring>
#include<cstdio>
#include<cmath>
using namespace std;
const int N=110;
double a[N][N];
const double eps=1e-8;
int n;

void print()
{
    for(int i=0;i<n;i++)
    {
        for(int j=0;j<=n;j++)
            printf("%.2f ",a[i][j]);
        puts("");
    }
}

int gauss()
{
    int r,c;
    for(r=0,c=0;r<n && c<n;r++,c++)
    {
        int t=r;
        for(int i=r+1;i<n;i++)
            if(fabs(a[i][c]) > fabs(a[t][c]))
                t=i;
        if(fabs(a[t][c]) < eps)
        {
            r--;
            continue;
        }
        for(int i=c;i<=n;i++) 
            swap(a[r][i],a[t][i]);

        for(int i=n;i>=c;i--) a[r][i]/=a[r][c];

        for(int i=r+1;i<n;i++)
            if(fabs(a[i][c]) > eps)
                for(int j=n;j>=c;j--)
                    a[i][j]-=a[r][j]*a[i][c];
    }


    for(int i=r;i<n;i++)
        if(fabs(a[i][n]) > eps)
            return 0;

    if(r < n) return 2;

    for(int i=n-1;i>=0;i--)
        for(int j=i+1;j<n;j++)
            a[i][n] -= a[j][n]*a[i][j];
    return 1;    
}

int main()
{
    cin>>n;
    for(int i=0;i<n;i++)
        for(int j=0;j<=n;j++)
            scanf("%lf",&a[i][j]);

    int t=gauss();

    if(t == 0) puts("No solution");
    else if(t == 2) puts("Infinite group solutions");
    else 
    {
        for(int i=0;i<n;i++)
            printf("%.2f\n",a[i][n]);
    }
    return 0;
}

可以发现高斯消元总共有三层循环。时间复杂度就是 O(n^3)

如果最外层枚举 i 的时候，发现没有一个 a[j][i] 非零。
说明 a[j][i] 的系数是 0。
如果在第二步倒推 x 的值得时候等式右边也消成了 0.即 0 * x[i] = 0,也就是 x[i] 取任何值都不会影响这个方程组。
我们称 x[i] 为自由元。
一旦有自由元，就说明方程有无数解

但是如果在第二步倒推 x 的值得时候等式右边也消成了非0值 即 0 * x[i] = k （k≠0）
也就是 x[i] 取任何值都不能满足这个方程组。
此时这个方程组无解。

acwing884
高斯消元同样可以用来解 xor 方程组。只要把加减法改成 xor 即可。
每个系数/未知数的取值是 0 或 1。
此时如果方程有 k 个自由元。
那么就一共有 $2^k$ 组解。
code

poj2947
模意义下的方程组依然可以求解。
除法那步需要改变。
可以改为乘逆元。
或者求出两个数的 LCM，两个方程分别乘一个系数，使得两式的第一个系数均为 LCM，就可以相减消掉一个了。
code

acwing207
在 n 维空间中，给出球面上 n+1 个点的坐标，求出球心坐标。n <= 10

样例：
2
0 0
-1 1
1 0
输出：0.5 1.5

球心就是到球面上任意一点距离都相等的点。
n 维空间中，n + 1 个点可以确定一个球。
我们可以设这个球心的坐标是 (x[1], x[2], …, x[n]),它到球面上的 n + 1 个点的距离相等。

假设两个点坐标是 (a[1], a[2], …, a[n]), (b[1],b[2], …, b[n])，半径为 r
$(a[1]-x[1])^2 + (a[2]-x[2])^2 + … + (a[n]-x[n])^2 = r2$
$(b[1]-x[1])^2 + (b[2]-x[2])^2 + … + (b[n]-x[n])^2 = r2$
两式相减，得到：
(a[1]-b[1])(a[1]+b[1]-2x[1]) + (a[2]-b[2])(a[2]+b[2]-2x[2]) + … + (a[n]-b[n])(a[n]+b[n]-2x[n]) = 0
$a[1]^2-b[1]^2-2x[1] (a[1]-b[1]) + a[2]^2-b[2]^2-2x[2] (a[2]-b[2]) + … + a[n]^2-b[n]^2-2x[n] (a[n]-b[n])= 0$
可以发现这是 n 元 1 次方程。

现在一共有 n+1 个点。
第 i 个点和第 i+1 个点可以得到一个方程。
总共可以得到 n 个方程。
n 个方程，n 个未知数。
用高斯消元法即可求解。
时间复杂度 O(n^3)
code

acwing208
有N个相同的开关，每个开关都与某些开关有着联系，每当你打开或者关闭某个开关的时候，其他的与此开关相关联的开关也会相应地发生变化，即这些相联系的开关的状态如果原来为开就变为关，如果为关就变为开。
你的目标是经过若干次开关操作后使得最后N个开关达到一个特定的状态。
对于任意一个开关，最多只能进行一次开关操作。你的任务是，计算有多少种可以达到指定状态的方法。（不计开关操作的顺序）

设xi表示第i个开关的操作情况，xi=1表示按了这个开关，xi=0表示没有按，再统计a[i][j],表示第i个开关和第j个开关的联系情况，a[i][j]=1表示按下j会影响i的状态，a[i][j]=0表示不会影响，特别的,a[i][i]=1;

一个开关最后的状态dsti，取决于它最初的状态srci,以及所有与它联系的开关的操作情况执行异或运算得到的结果。

code

容斥原理