A. EhAb AnD gCd

当取 $a = 1, b = x - 1$ 时，$gcd(a, b) = 1, lcm(a, b) = x - 1$，所以 $gcd(a, b) + lcm(a, b) = x$ 满足题意。

# include <iostream>

using namespace std;

int main()
{
    int T;
    cin >> T;
    while (T--) {
        int x;
        cin >> x;
        cout << 1 << ' ' << x - 1 << endl;
    }
    return 0;
}

B. CopyCopyCopyCopyCopy

由题意易得，只需要在重复的第一段中选择最小的数，在重复的第二段中选择第二小的数，以此类推即可。

由于要使选出的数严格递增，所以最终答案为原数组中各不相同的数的个数。

# include <iostream>
# include <unordered_set>
# include <algorithm>

using namespace std;

int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0), cout.tie(0);
    int T;
    cin >> T;
    while (T--) {
        int n;
        unordered_set<int> nums;
        cin >> n;
        while (n--) {
            int x;
            cin >> x;
            nums.insert(x);
        }
        cout << nums.size() << endl;
    }
    return 0;
}

C. Ehab and Path-etic MEXs

根据题意可以发现，在边上填数的时候，要尽可能的让从 $0$ 开始出现的连续的数字尽可能少，满足这一点首先就得让 $0$ 与 $1$ 间隔尽量远，而树上最远的距离是直径，所以我们可以将 $0$ 与 $1$ 分别填在直径最两侧的边上。

其次，对于这条直径上其它的边，一旦存在数字 $2$，则该条直径的 $MEX$ 值就会变为 $3$，在此基础上一旦存在数字 $3$，$MEX$ 值又会增加。因此，要使这条直径上剩余的边尽可能不出现 $2$，根据贪心的思想，从 $n - 2$ 开始依次递减着填数即可。

最后剩下的就是非直径上的边，由于 $0$ 与 $1$ 在直径的最两端，所以剩余的边无论怎么填数都不会使答案变差，而为了代码实现起来不复杂，可以在填完直径的数之后，依旧依次递减着将数填进剩余的边。

特殊的，如果只有两个点一条边，则直接输出 $0$ 即可。

# include <iostream>
# include <cstdio>
# include <cstring>
# include <algorithm>

using namespace std;

const int N = 1e5 + 5, M = 2e5 + 5;
int n;
int h[N], val[M], e[M], ne[M], idx;
int st, ed, dis;
int num, ans[N];

void add(int u, int v, int w)
{
    e[idx] = v, val[idx] = w, ne[idx] = h[u], h[u] = idx++;
}

void dfs(int u, int fa, int d)
{
    if (dis < d) {
        dis = d;
        ed = u;
    }
    for (int i = h[u]; ~i; i = ne[i]) {
        int j = e[i];
        if (j == fa)
            continue;
        dfs(j, u, d + 1);
    }
    return;
}

bool dfs_line(int u, int fa)
{
    for (int i = h[u]; ~i; i = ne[i]) {
        int j = e[i];
        if (j == fa)
            continue;
        if (j == ed) {
            ans[val[i]] = 1;
            return true;
        }
        if (dfs_line(j, u)) {
            if (u == st)
                ans[val[i]] = 0;
            else
                ans[val[i]] = num--;
            return true;
        }
    }
    return false;
}

void dfs_last(int u, int fa)
{
    for (int i = h[u]; ~i; i = ne[i]) {
        int j = e[i];
        if (j == fa)
            continue;
        if (ans[val[i]] == -1)
            ans[val[i]] = num--;
        dfs_last(j, u);
    }
    return;
}

int main()
{
    scanf("%d", &n);
    memset(h, -1, sizeof h);
    for (int i = 1; i < n; i++) {
        int u, v;
        scanf("%d %d", &u, &v);
        add(u, v, i);
        add(v, u, i);
    }
    if (n == 2) {
        cout << 0 << endl;
        return 0;
    }
    st = 1, dis = 0;
    dfs(st, -1, 0);
    st = ed, dis = 0;
    dfs(st, -1, 0);
    num = n - 2;
    memset(ans, -1, sizeof ans);
    dfs_line(st, -1);
    dfs_last(st, -1);
    for (int i = 1; i < n; i++)
        printf("%d\n", ans[i]);
    return 0;
}

D. Ehab the Xorcist

根据异或运算的性质可以发现，几个数异或的结果一定小于等于这几个数中的最大值，因此，如果 $u > v$ 则一定无解。

同时也不难发现，如果 $u, v$ 的奇偶性不同，则最终总会多一个或者少一个 $1$ ，所以此时也无解。

而当 $u = v$ 时，一个数 $u$ 即为答案。特殊的，题目要求构造的数组中的数字为正数，所以当 $u = v = 0$ 时，让数组中不含数字即可。

剩余的情况即为：$u < v$ 同时 $u, v$ 奇偶性相同（$v - u$ 一定为偶数）。

令 $w = v - u >> 1$，不难发现 $u, w, w$ 一定满足题意。在此基础上，如果 $u$ 与 $w$ 的二进制中 $1$ 的位置互不相同，则可以将 $u, w$ 合并，即只需要两个数 $u + w, w$ 即可满足题意。

那么能否将 $w, w$ 合并，使 $u, w + w$ 合法？显然只有当 $w = 0$ 时成立，此时 $u = v$ 与前提条件 $u < v$ 矛盾。

综上，此题只需要会 if else 即可 $AC$. （根本就不需要另外写个函数判断 $u 与 w 的二进制中 1 的位置是否互不相同 $，只需要判断 $u + w, w$ 是否合法即可）

$PS:$ 在这场 $cf$ 的官方题解中用到了 $a + b = a \oplus b + 2 \times (a \& b)$ 来推，奈何蒟蒻数学并没有学好，给不出具体证明，只能想到上述通俗易懂的方式。

# include <iostream>

using namespace std;

typedef long long LL;

int main()
{
    LL a, b;
    cin >> a >> b;
    if (a > b || a % 2 != b % 2)
        cout << -1 << endl;
    else if (a == b)
        if (!a)
            cout << 0 << endl;
        else
            cout << 1 << endl << a << endl;
    else {
        LL c = b - a >> 1;
        if (((a + c) ^ c) == a)
            cout << 2 << endl << a + c << ' ' << c << endl;
        else
            cout << 3 << endl << a << ' ' << c << ' ' << c << endl;
    }
    return 0;
}

E. Ehab’s REAL Number Theory Problem

一个正整数一定可以唯一拆分成如下形式：
$$ p_1^{c_1} \cdot p_2^{c_2} \cdot … \cdot p_k^{c_k} $$
其中 $p_i$ 为质数，$c_i$ 为非负整数次幂。

我们来考虑三个最小质数的乘积 $2 \times 3 \times 5 = 30$，经过计算发现，$30$ 含有 $8$ 个约数，以此类推不难发现，只要经过上述分解后质数个数大于等于 $3$ 个的数，就至少含有 $8$ 个约数。而题目给出的数组 $a$ 中的每一个数字最多只含有 $7$ 个约数，因此，将每个数经过上述分解之后，最多只会剩下两个质数。

令拆分后的结果为 $p^a, q^b$.

首先来考虑单个质数的不同次方有什么性质，以 $p^a$ 为例，如果 $a$ 为偶数，则 $p^a$ 本身就是个完全平方数；如果 $a$ 为奇数，则 $p^a \cdot p$ 一定是一个完全平方数，此时只需要考虑 $p^1$ 即可。即：如果 $a$ 为奇数，则可以将 $p^a$ 当做 $p$ 来处理，只需要找到另外一个 $p^b(b \& 1 = 1)$ ，则这两个数相乘就一定是完全平方数。

接下来来分类讨论 $a, b$ 的奇偶性：

• 显然，$0$ 也是偶数，下文的讨论中偶数当然也包含 $0$，当出现 $p^0$ 时就表明，这个数分解后不足 $2$ 个质数。
• $a$ 是奇数，$b$ 是奇数：原数可以当成 $p \cdot q$.
• $a$ 是奇数，$b$ 是偶数：原数可以当成 $p \cdot 1$.
• $a$ 是偶数，$b$ 是奇数：原数可以当成 $1 \cdot q$.
• $a$ 是偶数，$b$ 是偶数：原数就是一个完全平方数，只需要选该数即可，即：答案为 $1$.

我们再来考虑这样构建一张图：

以质数为点，上述讨论的乘积关系为无向边，如：当 $a, b$ 都为奇数时，连一条 $p, q$ 之间的无向边，该边的含义为：将 $p$ 与 $q$ 相乘的结果就相当于得到原数组当中的一个数，即：选了一条边等价于选了原数组当中的一个数，显然，每条无向边只能被选择一次。

要使选出的数最终相乘得到一个完全平方数，就相当于在图上选了一些边，使这些边相连的顶点均出现偶数次，即：这些边相连成环。最小环的长度即为最终答案。

那么如何用代码来实现这个操作？

选一条边相当于选一个数，可以看作每条边的权值均为 $1$，然后将每个点作为起点，做一遍 $BFS$，当遍历到已经遍历过的点时，两个点都反向找起点，记录所经历的边的数量，用它来更新答案即可。

聪明的小朋友很容易能想到如下图的情况：

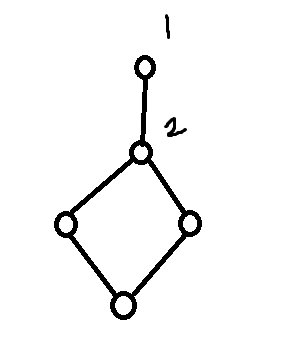
当 $1$ 作为起点时，经过上述操作得到的数量会比图中环的边数多 $2$.

但是由于我们是取最小值，所以存在这种情况并不会影响最终答案，因为在 $2$ 作为起点时可以正确得到这个环的边数。

还有一个需要注意的地方就是，在每次搜索过程中，第一次找到的环是否就一定是以当前点为起点的最小环？

答案是否定的，如下图所示：

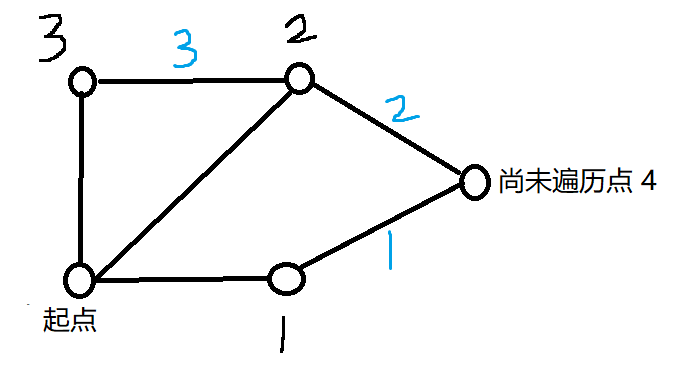
$1, 2, 3$ 号点均为当前队列中的点，同时在队列中的位置也如标号所示。

首先从对头取出 $1$ 号点，用它通过 $1$ 号边遍历 $4$ 号点，$4$ 号点入队。

接着，从对头取出 $2$ 号点，用 $2$ 号边来访问 $4$ 号点，发现 $4$ 号点已经被遍历过了，然后回头找环，找到环的大小为 $4$.

如果第一次找到环就结束搜索，那么就会错失正确答案。

若找到环之后只是用它来更新答案，但却不退出整个搜索，则会接着通过 $3$ 号边访问 $3$ 号点，此时找环，发现环的大小只有 $3$.

但是，如果对于枚举的每个作为起点的点，都要遍历一遍整张图，那么搜索量会很大，我们需要想一个剪枝，来减少搜索量。

根据 $BFS$ 的性质可以发现，当前点 $t$ 如果遍历到了一个已经遍历过的点 $j$，设 $dis_t, dis_j$ 分别为两点到起点的距离。这两个距离之间的关系只有可能为如下两种情况：

• $dis_t + 1= dis_j$
• $dis_t = dis_j$

假设记录的全局最优解为 $res$，则当 $dis_t + dis_j + 1 \geq res$ 时即可退出搜索（这里的 $+1$ 是加上从 $t$ ~ $j$ 的边），即判断是否满足 $2 \cdot dis_t + 1 \geq res$.

由于记录了 $dis$ 数组，那么在遍历到已被遍历过的点时，可以直接用 $dis_t + dis_j + 1$ 来更新答案，而不需要一开始分析的那样两个点都反向找起点，记录边数总和再更新。

最后剩下的问题就是，题目给出的数字的范围为 $10^6$.

虽然只用枚举这个范围内的质数作为起点，但量似乎仍有点多？

再回过来看 $p, q$，可以发现 $p \cdot q > 10^6$ 是不可能发生的，即对于所有 $p \cdot q > 10^6$ 的 $p, q$ 之间一定不会有边。也就是说，当两个质数 $p, q$ 之间有边，则 $p, q \leq 1000$.

而如果质数 $p, p > 1000$ 在某个环上，则这个环必定是 $1$ ~ $p$ ~ $1$ 的环，这种情况下，在枚举 $1$ 为起点的时候就能枚举到。

所以，在枚举起点时，只需要枚举 $1000$ 以内的质数以及 $1$ 即可。

而至于时间复杂度的话，因为有搜索剪枝的存在，所以比较玄学，最坏情况下大概是 $1000$ 以内质数个数 $+1$ 再乘以该图的边数吧（点可以经过多次，但一条无向边只能走一次）。

（你以为这么容易就会给你代码嘛，接下去是吐槽时间：

蒟蒻从前一天傍晚开始读这题，恰完晚饭之后在官方题解的帮助下搞懂了如何建图，然后开始写这题（没有看完整篇题解，搞懂了建图后就开始自己写）。由于蒟蒻是在太菜了，想当然认为搜索过程中搜到的第一个环就是最小的，然后 $WA$，$WA$ 了半个多小时不知道咋 $WA$ 了就接着看后半篇官方题解，题解中说用 $BFS$，（我一开始自己写用的是 $DFS$），然后我就改改改，改成了 $BFS$，改完之后竟然 $WA$ 在了同一个点上？？？

再瞅瞅题解再看看代码，不知道哪里写炸了，又看了好久，又交了几发，依然 $WA$ 在同一个点，心态爆炸睡觉去了 (╥╯^╰╥)

第二天一大早就醒了，继续 $debug$，无奈之下写了个对拍，然后自己随机的几百个 $test$ 都 $AC$ 了？？？$cf$ 上的是啥神仙数据啊

更加无奈之下自己在草稿纸上画画画，然后画出了上文的图，把 $BFS$ 内找到第一个环之后 $break$ 删了，然后交一发，$TLE$ 了，之后灵光乍现加了个剪枝，顺利 $AC$，再看一看自己的对拍，在自己 $AC$ 之后瞬间找到了一组数据，ε=(´ο｀*)))唉。然后一翻数据，是自己暴力写炸的原因导致的输出文件不一致 (╥╯^╰╥) （之前为什么不直接粘一份大佬 $AC$ 的代码用来拍呢

后来一想，之前的 $DFS$ 在找到第一个环之后不直接结束搜索应该也是可以的，然而蒟蒻懒得在提交记录里面翻代码了，就这样吧 (╥╯^╰╥)

打开 $markdown$ 继续写题解，发现之前关机的时候没保存，$C, D$ 的题解全没了，如果您觉得 $C, D$ 的题解写的不好，全是这题的锅，跟蒟蒻没关系）

吐槽完了，真好，睡了个午觉下午快没了，不知道半个下午加一个晚上够不够肝出来最后一题 ε=(´ο｀*)))

# include <iostream>
# include <cstdio>
# include <cstring>
# include <queue>
# include <unordered_set>
# include <algorithm>

using namespace std;

const int N = 1e6 + 5, M = 2e6 + 5, INF = 0x3f3f3f3f;
int n, res, dis[N];
unordered_set<int> nums;
int h[N], e[M], ne[M], idx;
bool vis[M];

void add(int u, int v)
{
    e[idx] = v, ne[idx] = h[u], h[u] = idx++;
}

void init()
{
    for (int i = 1; i < N; i++)
        dis[i] = -1;
    for (int i = 0; i < idx; i++)
        vis[i] = false;
    return;
}

void bfs(int st)
{
    init();
    queue<int> q;
    q.push(st);
    dis[st] = 0;
    while (!q.empty()) {
        int t = q.front();
        q.pop();
        if (2 * dis[t] + 1 >= res)
            break;
        for (int i = h[t]; ~i; i = ne[i]) {
            int j = e[i];
            if (vis[i])
                continue;
            vis[i] = vis[i ^ 1] = true;
            if (dis[j] != -1)
                res = min(res, dis[t] + dis[j] + 1);
            else {
                dis[j] = dis[t] + 1;
                q.push(j);
            }
        }
    }
    return;
}

int main()
{
    scanf("%d", &n);
    memset(h, -1, sizeof h);
    nums.insert(1);
    while (n--) {
        int x;
        scanf("%d", &x);
        int p, q;
        p = q = 0;
        for (int i = 2; i <= x / i; i++)
            if (x % i == 0) {
                int s = 0;
                while (x % i == 0) {
                    s++;
                    x /= i;
                }
                if (s & 1)
                    if (!p)
                        p = i;
                    else
                        q = i;
            }
        if (x > 1)
            if (!p)
                p = x;
            else
                q = x;
        if (p && p <= 1000)
            nums.insert(p);
        if (q && q <= 1000)
            nums.insert(q);
        if (p && q)
            add(q, p), add(p, q);
        else if (q)
            add(1, q), add(q, 1);
        else if (p)
            add(1, p), add(p, 1);
        else {
            cout << 1 << endl;
            return 0;
        }
    }
    res = INF;
    for (auto t : nums)
        bfs(t);
    if (res == INF)
        res = -1;
    printf("%d\n", res);
    return 0;
}

F. Ehab’s Last Theorem

首先，成环的这个比较好判，在 $DFS$ 过程中找大小满足要求的环即可，当然，用上一题的 $BFS$ 貌似也可以（如果你能解决上图 $1$ 的问题并在时间复杂度允许的情况下）。如果能够找到满足要求的环，则直接输出这个环。

如果找不到满足条件的环的话再来看如何找 $\lceil \sqrt{n}\ \rceil$ 个独立集？

如果这是一棵树的话，将奇数层的节点放在一起就一定是一个独立集，同理，偶数层的节点放在一起也一定是一个独立集。

那么这种做法能否类似的转移到图上？

令距离起点距离为奇数的点放在一起作为独立集，同理，距离为偶数的点放在一起作为一个独立集，那么在不存在满足条件的环的前提下，这样的做法能否一定找到解？

奈何蒟蒻不会证明这一点，而蒟蒻也看不太懂官方的题解，题解中也是将一个点和其相连的点标记成两个集合，然后输出。

至此，鸽了好久的 $F$ 题题解就这么水过去了？今晚 $cf$ 快开场了，就先不想咋证明了，等过两天周末了再找大佬学习一下，如果能证明会来更新。

# include <iostream>
# include <cstdio>
# include <cstring>
# include <vector>
# include <unordered_set>
# include <algorithm>

using namespace std;

const int N = 1e5 + 5, M = 4e5 + 5;
int n, m, k, dis[N];
int h[N], e[M], ne[M], idx;
vector<int> zero, one, path;
bool st[N], vis[N];

void add(int u, int v)
{
    e[idx] = v, ne[idx] = h[u], h[u] = idx++;
}

int get_bound()
{
    int l = 1, r = 1000;
    while (l < r) {
        int mid = l + r >> 1;
        if (mid * mid >= n)
            r = mid;
        else
            l = mid + 1;
    }
    return l;
}

bool dfs_path(int u, int fa, int d)
{
    if (dis[u]) {
        if (d - dis[u] >= k) {
            path.push_back(u);
            return true;
        }
        return false;
    }
    dis[u] = d;
    for (int i = h[u]; ~i; i = ne[i]) {
        int j = e[i];
        if (j == fa)
            continue;
        if (dfs_path(j, u, d + 1)) {
            path.push_back(u);
            return true;
        }
    }
    return false;
}

void dfs(int u, int fa)
{
    if (vis[u])
        return;
    vis[u] = true;
    if (!st[u]) {
        zero.push_back(u);
        for (int i = h[u]; ~i; i = ne[i]) {
            int j = e[i];
            if (!st[j]) {
                st[j] = true;
                one.push_back(j);
            }
        }
    }
    for (int i = h[u]; ~i; i = ne[i]) {
        int j = e[i];
        if (j == fa)
            continue;
        dfs(j, u);
    }
    return;
}

int main()
{
    scanf("%d %d", &n, &m);
    k = get_bound();
    memset(h, -1, sizeof h);
    while (m--) {
        int u, v;
        scanf("%d %d", &u, &v);
        add(u, v);
        add(v, u);
    }
    dfs_path(1, -1, 1);
    if (path.size()) {
        int cnt = 0;
        for (auto t : path) {
            if (vis[t])
                break;
            vis[t] = true;
            cnt++;
        }
        printf("2\n%d\n", cnt);
        for (int i = 0; i < cnt; i++)
            printf("%d%c", path[i], " \n"[i + 1 == cnt]);
    }
    else {
        dfs(1, -1);
        int zs = zero.size();
        printf("1\n");
        for (int i = 0; i < k; i++)
            printf("%d%c", zs >= k ? zero[i] : one[i], " \n"[i + 1 == k]);
    }
    return 0;
}