题目描述

有一个叫做“数码世界”奇异空间，在数码世界里生活着许许多多的数码宝贝，其中有些数码宝贝之间可能是好朋友，
并且数码宝贝世界有两条不成文的规定：

第一，数码宝贝A和数码宝贝B是好朋友等价于数码宝贝B与数码宝贝A是好朋友

第二，如果数码宝贝A和数码宝贝C是好朋友，而数码宝贝B和数码宝贝C也是好朋友，那么A和B也是好朋友

现在给出这些数码宝贝中所有好朋友的信息，问：可以把这些数码宝贝分成多少组，满足每组中的任意两个
数码宝贝都是好朋友，而且任意两组之间的数码宝贝都不是好朋友

输入格式

输入的第一行有两个正整数n(n <= 100)和m(m <= 100)，分别表示数码宝贝的个数和好朋友的组数，
其中数码宝贝编号为1~n

接下来有m行，每行两个正整数a和b，表示数码宝贝a和数码宝贝b是好朋友

输出格式

输出一个整数，表示这些数码宝贝可以分成的组数

样例输入

7 5
1 2
2 3
3 1
1 4
5 6

样例输出

3

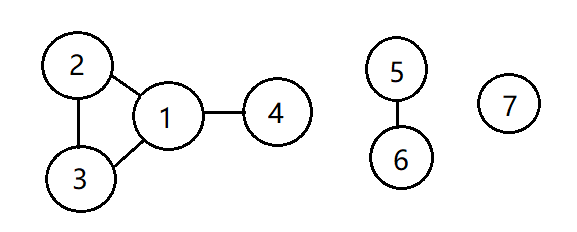
样例示例图

C++代码

#include<iostream>
using namespace std;

const int N = 100;

int a, b, m, n;             //m, n分别为组数和个数  a, b表示每次在同一个集合的两个数
int father[N];              //集

//在合并之前初始化每个节点为该集合的根节点(每个数都是一个集合)
void init(int n) {
    for (int i = 1; i <= n; i ++ ) father[i] = i;
}

//找到元素x在该集合中的根节点(根节点满足x == father[x])
int findFather(int x) {     //查
    int a = x;  //记录初始节点
    while (x != father[x]) x = father[x];   //循环结束后的x为该集合的根节点
    //路径压缩，将寻找根节点路途中的每个节点指向其根节点，优化之后的查找速度，可不写
    while (a != father[a]) {
        int b = a;      //记录a，防止后面被覆盖
        a = father[a];  //让a指向其父节点
        father[b] = x;  //指向根节点
    }
    return x;
}

//将a b合并到一个集合中
void Union(int a, int b) {  //并
    //分别找到a, b所在结合的根节点
    int Ra = findFather(a);
    int Rb = findFather(b);
    //当a, b不在同一个集合中时将Ra指向Rb或者将Rb指向Rb指向ba
    if (Ra != Rb) {
        father[Ra] = Rb;    //将Ra指向Rb
        //father[Rb] = Ra; 也可以
    }
}

int main() {
    cin >> n >> m;
    init(n);    //在合并集合之前需初始化，勿遗忘
    while (m -- ) {
        cin >> a >> b;
        Union(a, b);    //每输入两个数，将其合并到一个集合中
    }
    int ans = 0;    //用来记录集合的个数
    //遍历所有数，根节点的数量即为集合的数量
    for (int i = 1; i <= n; i ++ ) {
        if (i == findFather(i)) ans ++ ;    //i为其所在结合的根节点
    }
    cout << ans << endl;
    return 0;
}