单源最短路径

Dijkstra算法

1、初始化 dis[1] = 0, 其余节点得 dis 值为正无穷大

2、找出一个未被标记得、 dis[x] 最小的节点 x，然后标记节点 x

3、扫描节点 x 的所有出边 (x, y, z)，若 dis[y] > dis[x] + z, 则使用 dis[x] + z 更新 dis[y]

4、重复上述 2 ~ 3 两个步骤，直到所有节点都被标记

dijkstra算法只适用于所有边的长度都是非负数的图。当边长 z 都是非负数时，全局最小值不可能再被其他节点更新，故再第 1 步中选出的节点 x 必然满足：dis[x] 已经是起点到 x 的最短路径。我们不断选择全局最小值进行标记和扩展，最终可得到起点 1 到每个节点的最短路径的长度

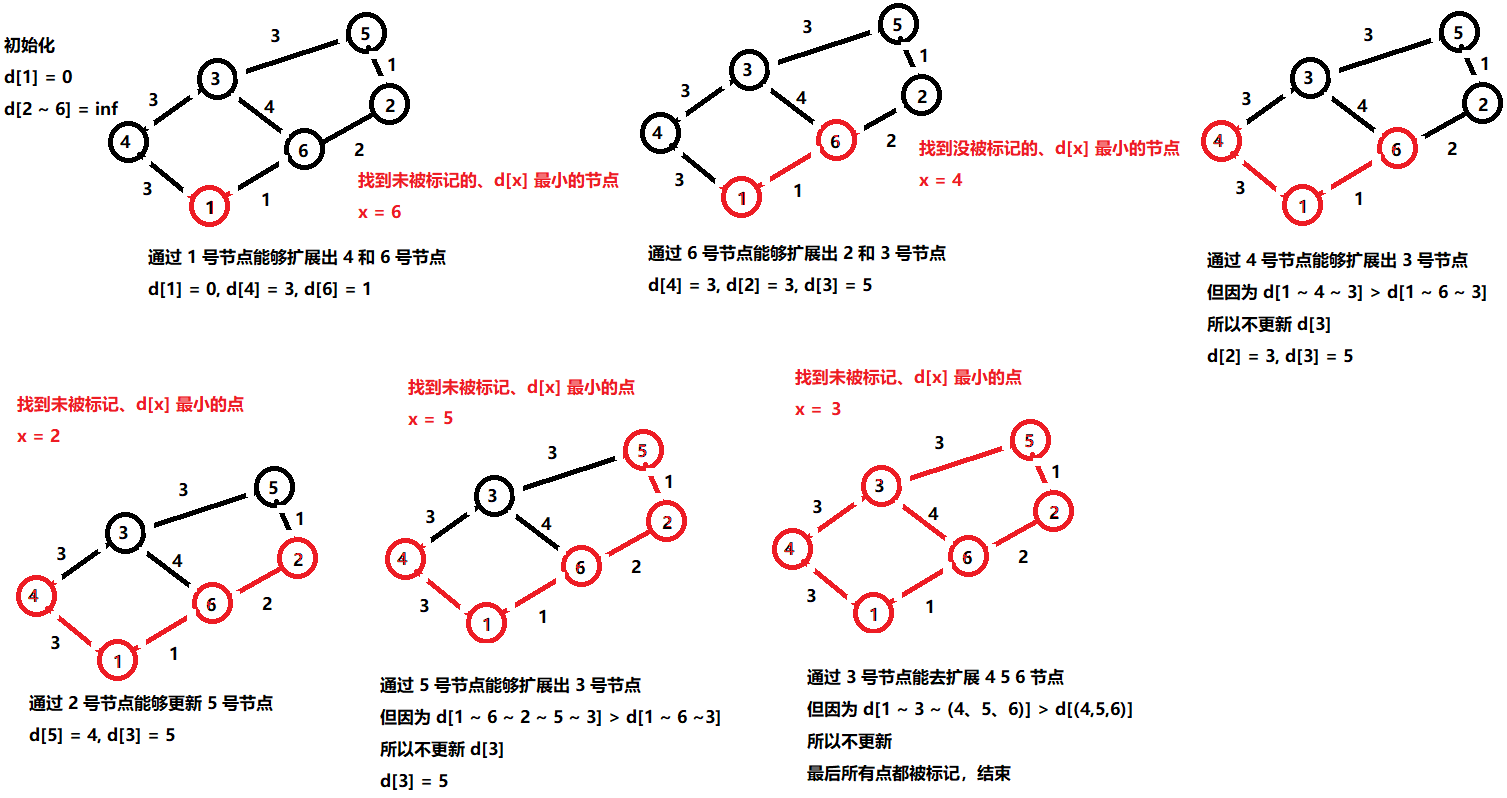
void dijkstra()
{
    memset(d, 0x3f, sizeof d);
    memset(st, 0, sizeof st);
    d[1] = 0;
    for(int i = 1; i < n; i ++){
        int x = -1;
        for(int j = 1; j <= n; j ++)
            if(!st[j] && (x == -1 || d[j] < d[x]))  x = j;
        st[x] = 1;
        for(int j = 1; j <= n; j ++)
            d[j] = min(d[j], d[x] + g[x][j]);
    }
}

堆优化 dijkstra 算法

可以用二叉堆对 d 数组进行维护，每次在二叉堆中取出最小值并从堆中删除。

void dijkstra()
{
    memset(d, 0x3f, sizeof d);
    memset(st, 0, sizeof st);
    d[1] = 0;
    priority_queue < pair < int , int > > q;
    q.push({0, 1});
    while(q.size()){
        int t = q.top().second;
        q.pop();
        if(st[t])   continue;
        st[t] = 1;
        for(int i = h[t]; ~i; i = ne[i]){
            int v = e[i], z = w[i];
            if(d[v] > d[t] + z){
                d[v] = d[t] + z;
                q.push({-d[v], v});
            }
        }
    }
}

Bellman-Ford 算法

给定一张有向图，若对于图中的某一条边(x, y, z), 有 d[y] <= d[x] + z 成立，则称该边满足三角形不等式。若所有边都满足三角形不等式，则 d 数组就是所求最短路。

1、扫描所有边(x, y, z), 若 d[y] > d[x] + z, 则用 d[x] + z 更新 d[y]。

2、重复上述步骤，直到没有更新发生。

struct node{
    int a, b, c;
}g[M];

void bellman()
{
    memset(d, 0x3f ,sizeof d);
    d[1] = 0;
    for(int i = 0; i < n; i ++){
        for(int j = 0; j < m; j ++){
            node t = g[j];
            d[t.b] = min(d[t.b], d[t.a] + t.c);
        }
    }
}

SPFA 算法 （队列优化的Bellman-Ford算法）

1、建立一个队列，最初队列中只含有起点 1

2、取出对头节点 x，扫描它的所有出边 (x, y, z)， 若 d[y] > d[x] + z, 则使用 d[x] + z 更新 d[y]。同时，若 y 不在队列中，则把 y 入队。

3、重复上述步骤，直到队列为空。

void spfa()
{
    memset(d, 0x3f, sizeof d);
    memset(st, 0, sizeof st);
    d[1] = 0;st[1] = 1;
    queue < int > q;
    q.push(1);
    while(q.size()){
        int t = q.front();q.pop();
         st[t] = 0;
        for(int i = h[t]; ~i; i = ne[i]){
            int v = e[i], z = w[i];
            if(d[v] > d[t] + z){
                d[v] = d[t] + z;
                if(!st[v])  q.push(v), st[v] = 1;
            }
        }
    }
}

热浪

给定起点和终点，询问起点到终点的最短路

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<queue>

using namespace std;

const int N = 2510, M = 6210 * 2 + 10;

int h[N], ne[M], e[M], w[M], idx;
int n, m, S, T, d[N];
bool st[N];

void add(int a, int b, int c)
{
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++;
}

void spfa()
{
    memset(d, 0x3f, sizeof d);
    queue < int > q;
    st[S] = 1;
    q.push(S);
    d[S] = 0;
    while(q.size()){
        int t = q.front();q.pop();
        st[t] = 0;
        for(int i = h[t]; ~i; i = ne[i]){
            int v = e[i], z = w[i];
            if(d[v] > d[t] + z){
                d[v] = d[t] + z;
                if(!st[v])  st[v] = 1, q.push(v);
            }
        }
    }
}

int main()
{
    memset(h, -1, sizeof h);
    cin >> n >> m >> S >> T;
    for(int i = 1; i <= m; i ++){
        int a, b, c;
        scanf("%d%d%d", &a, &b, &c);
        add(a, b, c), add(b, a, c);
    }

    spfa();

    cout << d[T] << endl;

    return 0;
}

信使

emmm…求起点到其余点的最短路的最大值

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<queue>

using namespace std;

const int N = 110, M = 210 * 2 + 10;
const int inf = 0x3f3f3f3f;

int h[N], ne[M], e[M], w[M], idx;
int n, m, d[N];
bool st[N];

void add(int a, int b, int c)
{
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++;
}

void spfa()
{
    memset(d, 0x3f, sizeof d);
    queue < int > q;
    q.push(1);
    st[1] = 1;
    d[1] = 0;
    while(q.size()){
        int t = q.front();q.pop();
        st[t] = 0;
        for(int i = h[t]; ~i; i = ne[i]){
            int v = e[i], z = w[i];
            if(d[v] > d[t] + z){
                d[v] = d[t] + z;
                if(!st[v])  st[v] = 1, q.push(v);
            }
        }
    }
}

int main()
{
    memset(h, -1, sizeof h);
    cin >> n >> m;
    for(int i = 1; i <= m; i ++){
        int a, b, c;
        scanf("%d%d%d", &a, &b, &c);
        add(a, b, c), add(b, a, c);
    }

    spfa();

    int res = 0;
    for(int i = 1; i <= n; i ++){
        if(d[i] > inf / 2){
            res = -1;
            break;
        }
        res = max(res, d[i]);
    }
    cout << res << endl;

    return 0;
}

香甜的黄油

以每一个点为起点，求该点到固定其余几个点的最短路径长度和的最小值

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<queue>

using namespace std;

const int N = 810, M = 1460 * 2 + 10;

int h[N], e[M], ne[M], w[M], idx;
int n, m, p, d[N], a[N];
bool st[N];

void add(int a, int b, int c)
{
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++;
}

int spfa(int s)
{
    memset(d, 0x3f, sizeof d);
    queue < int > q;
    q.push(s);
    d[s] = 0;
    st[s] = 1;
    while(q.size()){
        int t = q.front();q.pop();
        st[t] = 0;
        for(int i = h[t]; ~i; i = ne[i]){
            int v = e[i], z = w[i];
            if(d[v] > d[t] + z){
                d[v] = d[t] + z;
                if(!st[v])  st[v] = 1, q.push(v);
            }
        }
    }

    int num = 0;
    for(int i = 1; i <= p; i ++){
        num += d[a[i]];
    }
    return num;
}

int main()
{
    memset(h, -1, sizeof h);
    cin >> p >> n >> m;
    for(int i = 1; i <= p; i ++){
        cin >> a[i];
    }
    for(int i = 1; i <= m; i ++){
        int a, b, c;
        cin >> a >> b >> c;
        add(a, b, c), add(b, a, c);
    }

    int res = 0x3f3f3f3f;
    for(int i = 1; i <= n; i ++)    res = min(res, spfa(i));
    cout << res << endl;

    return 0;
}

最优乘车

对于每一条公交路线，可以由公交线路的每一个点出发向后面的每一个点连一条边权为 1 的边，然后求一次单源最短路，其中起点为 1 ，终点为 n 。 最后 d[n] - 1 就是答案

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<queue>
#include<sstream>

using namespace std;

const int N = 510;

int n, m, g[N][N], a[N], d[N];
bool st[N];

void spfa()
{
    memset(d, 0x3f, sizeof d);
    queue < int > q;
    q.push(1);
    d[1] = 0;
    st[1] = 1;
    while(q.size()){
        int t = q.front();q.pop();
        st[t] = 0;
        for(int i = 1; i <= n; i ++){
            if(g[t][i] && d[i] > d[t] + 1){
                d[i] = d[t] + 1;
                if(!st[i])  st[i] = 1, q.push(i);
            }
        }
    }
}

int main()
{
    cin >> m >> n;
    string line;
    getline(cin, line);
    for(int i = 1; i <= m; i ++){
        getline(cin, line);
        stringstream ssin(line);
        int cnt = 0, p;
        while(ssin >> p)    a[cnt ++ ] = p;
        for(int i = 0; i < cnt; i ++)
            for(int j = i + 1; j < cnt; j ++)
                g[a[i]][a[j]] = 1;
    }

    spfa();

    if(d[n] == 0x3f3f3f3f)  puts("NO");
    else    printf("%d\n", d[n] - 1);

    return 0;
}

昂贵的聘礼

1、建立一个超级源点 0 从超级源点先其余每个点连一条边，其边权值为直接购买该物品的价格，这样起点从 0 开始就代表我可以直接购买当前物品。

2、由每个物品的代替品向该物品连一条有向边，其边权值为该代替品花费多少钱可以得到物品的价格，这样当我从起点 0 直接购买当前物品之后就可以拿着这个代替品去购买上一级的物品。

需要注意的就是等级限制，枚举一个区间范围就是第 1 个物品的等级 - m ([level[1] - m, level[1]]) 每次更新最短路的时候，只更新 [i, i + m] 范围内的物品

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<queue>

using namespace std;

const int N = 110;
const int inf = 0x3f3f3f3f;

int g[N][N], d[N], n, m, lev[N];
bool st[N];

int spfa(int l, int r)
{
    memset(d, 0x3f, sizeof d);
    queue < int > q;
    d[0] = 0;
    st[0] = 1;
    q.push(0);
    while(q.size()){
        int t = q.front();q.pop();
        st[t] = 0;
        for(int i = 1; i <= n; i ++){
            if(lev[i] >= l && lev[i] <= r){
                if(d[i] > d[t] + g[t][i]){
                    d[i] = d[t] + g[t][i];
                    if(!st[i])  st[i] = 1, q.push(i);
                }
            }
        }
    }
    return d[1];
}

int main()
{
    cin >> m >> n;
    memset(g, 0x3f, sizeof g);
    for(int i = 1; i <= n; i ++) g[i][i] = 0;
    for(int i = 1; i <= n; i ++){
        int p, x;
        cin >> p >> lev[i] >> x;
        g[0][i] = min(g[0][i], p);
        for(int j = 0; j < x; j ++){
            int id, p1;
            cin >> id >> p1;
            g[id][i] = min(g[id][i], p1);
        }
    }

    int res = inf;
    for(int i = lev[1] - m; i <= lev[1]; i ++)  res = min(res, spfa(i, i + m));
    cout << res << endl;

    return 0;
}

新年好

最短路 + 爆搜

因为无法一次就处理出从自己家出发，拜访每个亲戚（顺序任意）的最短路，但因为需要访问的点数较少，所以可以进行暴力枚举排列组合。

1、先算出 6 个点的单源最短路

2、dfs 暴力枚举排列组合求出最短路的方案

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<queue>

using namespace std;

const int N = 50010, M = 2e5 + 10;

int h[N], ne[M], e[M], w[M], idx;
int n, m, sco[10], d[10][N];
bool st[N];

void add(int a, int b, int c)
{
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++;
}

void dij(int s, int d[])
{
    memset(d, 0x3f, N * 4);
    memset(st, 0, sizeof st);
    priority_queue < pair < int , int > , vector < pair < int , int > > , greater < pair < int , int > > > q;
    q.push({0, s});
    d[s] = 0;
    while(q.size()){
        int t = q.top().second;q.pop();

        if(st[t])   continue;
        st[t] = 1;

        for(int i = h[t]; ~i; i = ne[i]){
            int v = e[i], z = w[i];
            if(d[v] > d[t] + z){
                d[v] = d[t] + z;
                q.push({d[v], v});
            }
        }
    }
}

int dfs(int u, int start, int dis)
{
    if(u > 5)   return dis;

    int res = 0x3f3f3f3f;
    for(int i = 1; i <= 5; i ++){
        if(!st[i]){
            st[i] = 1;
            res = min(res, dfs(u + 1, i, dis + d[start][sco[i]]));
            st[i] = 0;
        }
    }

    return res;
}

int main()
{
    memset(h, -1, sizeof h);
    cin >> n >> m;
    sco[0] = 1;
    for(int i = 1; i <= 5; i ++)    cin >> sco[i];
    for(int i = 1; i <= m; i ++){
        int a, b, c;
        cin >> a >> b >> c;
        add(a, b, c), add(b, a, c);
    }

    for(int i = 0; i <= 5; i ++)    dij(sco[i], d[i]);

    // for(int i = 0; i <= 5; i ++){
    //     for(int j = 1; j <= n; j ++)    cout << d[i][j] << " ";
    //     cout << endl;
    // }
    memset(st, 0, sizeof st);
    cout << dfs(1, 0, 0) << endl;

    return 0;
}

通信线路

答案具有单调性，因为支付的钱更多时，合法的升级方案一定包含了花费更少的升级方案。所以可以二分答案，将问题转化为：是否存在一种合法的升级方案，使花费不超过 mid。

check函数中， 可以将升级价格大于 mid 的电缆看作长度为 1 的边，把升级价格不超过 mid 的电缆看作长度为 0 的边，然后求从 1 到 n 的最短路是否不超过 k 即可。

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<queue>

using namespace std;

const int N = 1010, M = 20010;

int h[N], e[M], ne[M], w[M], idx;
int n, m, k, d[N];
bool st[N];

void add(int a, int b, int c)
{
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++;
}

bool check(int x)
{
    memset(d, 0x3f, sizeof d);
    memset(st, 0, sizeof st);
    deque < int > q;
    q.push_front(1);
    d[1] = 0;

    while(q.size()){
        int t = q.front();
        q.pop_front();

        if(st[t])   continue;
        st[t] = 1;

        for(int i = h[t]; ~i; i = ne[i]){
            int v = e[i], z = w[i];
            z = z > x;
            if(d[v] > d[t] + z){
                d[v] = d[t] + z;
                if(z)   q.push_back(v);
                else    q.push_front(v);
            }
        }
    }

    return d[n] <= k;
}

int main()
{
    memset(h, -1, sizeof h);
    cin >> n >> m >> k;
    for(int i = 1; i <= m; i ++){
        int a, b, c;
        cin >> a >> b >> c;
        add(a, b, c), add(b, a, c);
    }

    int l = 0, r = 1e6 + 1;
    while(l < r){
        int mid = l + r >> 1;
        if(check(mid))  r = mid;
        else    l = mid + 1;
    }

    if(l == 1e6 + 1)    cout << -1 << endl;
    else    cout << l << endl;

    return 0;
}

道路与航线

1、只把双向边加入到图中，用深度优先遍历划分图中的连通块，记 c[x] 为节点 x 所属的连通块的编号。

2、统计每个连通块的总入度（有多少条边从连通块之外指向连通块之内），记deg[i] 为第 i 个连通块的总入度

3、建立一个队列（存储连通块编号，用于拓扑排序），最初队列中包含所有总入度为零的连通块编号（当然其中也包括c[s])。设 d[x] = 0, 其余点的 d 值为无穷大

4、取出队头的连通块 i ，对该连通块执行堆优化的 dijkstra 算法。

​ （1）建立一个堆，把第 i 个连通块的所有节点加入堆中。

​ （2）从堆中取出 d[x] 最小的节点 x

​ （3）若 x 被扩展过，回到步骤 (2)，否则进入下一步

​ （4）扫描从 x 出发的所有边 (x, y, z)，用 d[x] + z 更新 d[y]

​ （5）若 c[x] == c[y] （仍在连通块中）并且d[y] 被更新，则把 y 插入堆

​ （6）若 c[x] != c[y]，则令 deg[c[y]] 减去 1.若减到了 0 ，则把c[y] 插入拓扑排序的队列末尾

​ （7）重复步骤 (2) ~ (6) 直到堆为空。

5、重复步骤 4，直到队列为空，拓扑排序完成

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<queue>

using namespace std;
typedef pair < int , int > pii;

const int N = 25010, M = 150010, inf = 0x3f3f3f3f;

int h[N], ne[M], e[M], w[M], idx;
int n, m, p, s, d[N], cnt, id[N], din[N];
vector < int > blo[N];
queue < int > q;
bool st[N];

void add(int a, int b, int c)
{
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++;
}

void dfs(int u)
{
    id[u] = cnt;
    blo[cnt].push_back(u);

    for(int i = h[u]; ~i; i = ne[i]){
        if(!id[e[i]])   dfs(e[i]);
    }
}

void dij(int u)
{
    priority_queue < pii, vector < pii > , greater < pii > > s;
    for(int i = 0; i < blo[u].size(); i ++){
        int v = blo[u][i];
        s.push({d[v], v});
    }

    while(s.size()){
        int t = s.top().second;s.pop();

        if(st[t])   continue;
        st[t] = 1;

        for(int i = h[t]; ~i; i = ne[i]){
            int v = e[i], z = w[i];
            if(d[v] > d[t] + z){
                d[v] = d[t] + z;
                if(id[v] == id[t])  s.push({d[v], v});
            }
            if(id[v] != id[t] && -- din[id[v]] == 0)    q.push(id[v]);
        }
    }
}

void topsort()
{
    memset(d, 0x3f, sizeof d);
    d[s] = 0;

    for(int i = 1; i <= cnt; i ++){
        if(!din[i])
            q.push(i);
    }

    while(q.size()){
        int t = q.front();q.pop();

        dij(t);
    }
}

int main()
{
    memset(h, -1, sizeof h);
    cin >> n >> m >> p >> s;
    for(int i = 1; i <= m; i ++){
        int a, b, c;
        cin >> a >> b >> c;
        add(a, b, c), add(b, a, c);
    }

    for(int i = 1; i <= n; i ++){
        if(!id[i]){
            cnt ++;
            dfs(i);
        }
    }

    for(int i = 1; i <= p; i ++){
        int a, b, c;
        cin >> a >> b >> c;
        din[id[b]] ++;
        add(a, b, c);
    }

    topsort();

    for(int i = 1; i <= n; i ++){
        if(d[i] > inf / 2)  puts("NO PATH");
        else    printf("%d\n", d[i]);
    }

    return 0;
}

最优贸易

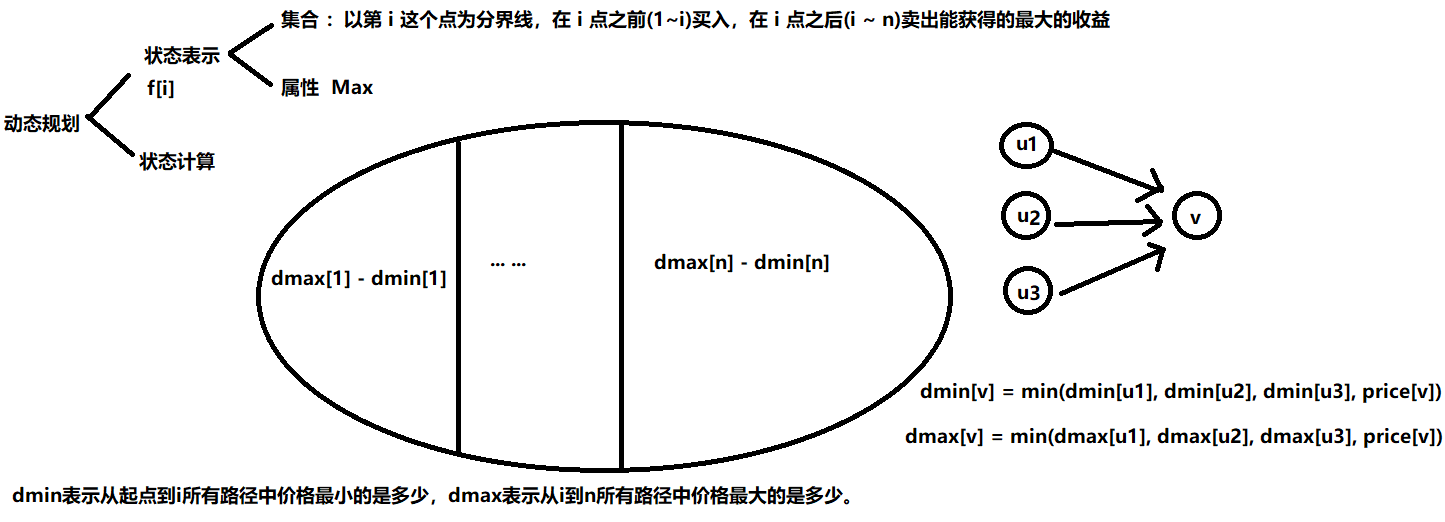
求 dmin[i] 和 dmax[i] 时，由于不是拓扑图，状态的更新可能存在环，因此不能使用动态规划，只能使用求最短路的方式。

不同的是，计算dmin 数组时起点是 1 号点，终点是 i。计算 dmax 数组时起点是 i 号点，终点是 n 号点（我们无法确定 i 号点是那个点，枚举的话时间复杂度就太高了）所以我们需要建立一个方向图。那么在反图中，n也能到i，从而dmax数组要从n开始算起。(同时可以保证买入点一定在卖出点之前，相当于以i为分界点，将整个区间划分成[1,i],[i,n])。

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<queue>

using namespace std;

const int N = 1e5 + 10, M = 1e6 + 10;

int h[N], rh[N], ne[M], e[M], idx, w[N];
int dmin[N], dmax[N], n, m;
bool st[N];

void add(int h[], int a, int b)
{
    e[idx] = b, ne[idx] = h[a], h[a] = idx ++;
}

void spfa()
{
    memset(dmin, 0x3f, sizeof dmin);
    queue < int > q;
    q.push(1);
    st[1] = 1;
    dmin[1] = w[1];
    while(q.size()){
        int t = q.front();q.pop();
        st[t] = 0;
        for(int i = h[t]; ~i; i = ne[i]){
            int v = e[i];
            if(dmin[v] > min(dmin[t], w[v])){
                dmin[v] = min(dmin[t], w[v]);
                if(!st[v])  st[v] = 1, q.push(v);
            }
        }
    }
}

void spfa1()
{
    memset(dmax, -0x3f, sizeof dmax);
    queue < int > q;
    q.push(n);
    st[n] = 1;
    dmax[n] = w[n];
    while(q.size()){
        int t = q.front();q.pop();
        st[t] = 0;
        for(int i = rh[t]; ~i; i = ne[i]){
            int v = e[i];
            if(dmax[v] < max(dmax[t], w[v])){
                dmax[v] = max(dmax[t], w[v]);
                if(!st[v])  st[v] = 1, q.push(v);
            }
        }
    }
}

int main()
{
    memset(h, -1, sizeof h);
    memset(rh, -1, sizeof rh);
    cin >> n >> m;
    for(int i = 1; i <= n; i ++)    cin >> w[i];
    for(int i = 1; i <= m; i ++){
        int a, b, c;
        cin >> a >> b >> c;
        add(h, a, b), add(rh, b, a);
        if(c == 2)  add(h, b, a), add(rh, a, b);
    }

    spfa();
    spfa1();

    int res = 0;
    for(int i = 1; i <= n; i ++)    res = max(res, dmax[i] - dmin[i]);
    cout << res << endl;

    return 0;
}

选择最佳线路

求多起点到任一终点的最短路。

方法一：建立超级源点，该超级源点到每个起点的边权为 0

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<queue>

using namespace std;

const int N = 1010, M = 40010;

int h[N], ne[M], e[M], w[M], idx;
int n, m, ed, d[N], p;
bool st[N];

void add(int a, int b, int c)
{
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++;
}

void spfa()
{
    memset(d, 0x3f, sizeof d);
    queue < int > q;
    q.push(0);
    st[0] = 1;
    d[0] = 0;
    while(q.size()){
        int t = q.front();q.pop();
        st[t] = 0;
        for(int i = h[t]; ~i; i = ne[i]){
            int v = e[i], z = w[i];
            if(d[v] > d[t] + z){
                d[v] = d[t] + z;
                if(!st[v])  st[v] = 1, q.push(v);
            }
        }
    }
}

int main()
{
    while(cin >> n >> m >> ed){
        memset(h, -1, sizeof h);
        for(int i = 1; i <= m; i ++){
            int a, b, c;
            cin >> a >> b >> c;
            add(a, b, c);
        }
        cin >> p;
        for(int i = 1; i <= p; i ++){
            int s;
            cin >> s;
            add(0, s, 0);
        }

        spfa();

        if(d[ed] == 0x3f3f3f3f) puts("-1");
        else    printf("%d\n", d[ed]);
    }

    return 0;
}

方法2：建反图，以终点为起点，最后在所以起点中遍历找出单源最短最小值

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<queue>

using namespace std;

const int N = 1010, M = 40010;

int h[N], ne[M], e[M], w[M], idx;
int n, m, p, d[N], ed;
bool st[N];

void add(int a, int b, int c)
{
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++;
}

void spfa()
{
    memset(d, 0x3f ,sizeof d);
    queue < int > q;
    q.push(ed);
    d[ed] = 0;
    st[ed] = 1;
    while(q.size()){
        int t = q.front();q.pop();
        st[t] = 0;
        for(int i = h[t]; ~i; i = ne[i]){
            int v = e[i], z = w[i];
            if(d[v] > d[t] + z){
                d[v] = d[t] + z;
                if(!st[v])  st[v] = 1, q.push(v);
            }
        }
    }
}

int main()
{
    while(cin >> n >> m >> ed){
        memset(h, -1, sizeof h);
        for(int i = 1; i <= m; i ++){
            int a, b, c;
            cin >> a >> b >> c;
            add(b, a, c);
        }

        spfa();

        cin >> p;
        int res = 0x3f3f3f3f;
        for(int i = 1; i <= p; i ++){
            int s;
            cin >> s;
            res = min(d[s], res);
        }
        if(res == 0x3f3f3f3f)   res = -1;
        cout << res << endl;
    }
    return 0;
}

最短路计数

可以将图抽象成一颗最短路树。最短路树：记录每个点由那几个点更新得来的，得到一根树。但因为这个最短路树是具有环的，所以不可能用 dp 的方式做。

因为树天生具有拓扑序，所以可以对树进行拓扑序的遍历

在我们对树进行拓扑序的顺序遍历的时候（也可以理解为按照层次遍历把），就可以得到每个点到根节点的最短距离，当我们从第 x 层扩展到第 y 层的时候，如果第 x 层有 z 个节点可以前往第 y 层的某一个节点，则第 4 层的该节点的最短路数就是 z 条。

比如 第 3 层的 5 号节点和 6 号节点都可以扩展到第 4 层的 7 号节点，那么 1 号节点能够通往 7 号节点的最短路条数就是 2 条。

BFS 只入队一次，出队一次。可以抽象成拓扑图
dijkstra 每个点只出队一次。也可以抽象成拓扑图。
spfa 本身不具备拓扑序，但如果图中存在负权边只能用该算法做。先跑一般spfa，再检查每个边是否满足dist[j]=dist[t]+w[i],若满足说明该边存在于最短路树上。再在最短路树上做一般DAG dp即可。

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<queue>

using namespace std;

const int N = 1e5 + 10, M = 4e5 + 10, mod = 100003;

int h[N], ne[M], e[M], idx;
int n, m, d[N], cnt[N];

void add(int a, int b)
{
    e[idx] = b, ne[idx] = h[a], h[a] = idx ++;
}

void bfs()
{
    memset(d, 0x3f ,sizeof d);
    queue < int > q;
    q.push(1);
    d[1] = 0;
    cnt[1] = 1;

    while(q.size()){
        int t = q.front();q.pop();

        for(int i = h[t]; ~i; i = ne[i]){
            int v = e[i];
            if(d[v] > d[t] + 1){
                d[v] = d[t] + 1;
                cnt[v] = cnt[t];
                q.push(v);
            }else if(d[v] == d[t] + 1)
                cnt[v] = (cnt[v] + cnt[t]) % mod;
        }
    }
}

int main()
{
    memset(h, -1, sizeof h);
    cin >> n >> m;
    for(int i = 1; i <= m; i ++){
        int a, b;
        cin >> a >> b;
        add(a, b), add(b, a);
    }

    bfs();

    for(int i = 1; i <= n; i ++)
        printf("%d\n", cnt[i]);

    return 0;
}

383. 观光

和上题差不多，现在每一个点多一种状态

d[i] [0] 存最短路径值 d[i] [1] 存次短路径值

1.d[v][0]>minx+w 更新最短距离（但是记得更新次短距离，次短距离一定大于d[v][0]，当d[v][0]更新成minx+w时，次短距离更新成原来的d[v][0]）

2.d[v][0]==minx+w 找到相同最短距离，更新最短条数

3.d[v][1]>minx+w 更新次短距离

4.d[v][1]==minx+w 找到相同次短距离，更新次短条数

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<queue>

using namespace std;

const int N = 1010, M = 10010;

int h[N], ne[M], e[M], w[M], idx;
int n, m, s, ed, T, d[N][2], cnt[N][2];
bool st[N][2];
struct node{
    int ver, type, dis;
    bool operator > (node t) const{
        return dis > t.dis;
    }
};
void add(int a, int b, int c)
{
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++;
}

int dij()
{
    memset(st, 0, sizeof st);
    memset(cnt, 0, sizeof cnt);
    memset(d, 0x3f, sizeof d);
    priority_queue < node , vector < node > , greater < node > > q;
    q.push({s, 0, 0});
    d[s][0] = 0, cnt[s][0] = 1;
    while(q.size()){
        node a = q.top();q.pop();
        int t = a.ver, ty = a.type, dis = a.dis, count = cnt[t][ty];
        if(st[t][ty])   continue;
        st[t][ty] = 1;
        for(int i = h[t]; ~i; i = ne[i]){
            int v = e[i], z = w[i];
            if(d[v][0] > dis + z){
                d[v][1] = d[v][0];cnt[v][1] = cnt[v][0];
                q.push({v, 1, d[v][1]});
                d[v][0] = dis + z;cnt[v][0] = count;
                q.push({v, 0, d[v][0]});
            }else if(d[v][0] == dis + z){
                cnt[v][0] += count;
            }else if(d[v][1] > dis + z){
                d[v][1] = dis + z;cnt[v][1] = count;
                q.push({v, 1, d[v][1]});
            }else if(d[v][1] == dis + z){
                cnt[v][1] += count;
            }
        }
    }

    int res = cnt[ed][0];
    if(d[ed][1] == d[ed][0] + 1)    res += cnt[ed][1];
    return res;
}

int main()
{
    cin >> T;
    while(T --){
        memset(h, -1, sizeof h);
        cin >> n >> m;
        for(int i = 1; i <= m; i ++){
            int a, b, c;
            scanf("%d%d%d", &a, &b, &c);
            add(a, b, c);
        }
        cin >> s >> ed;

        printf("%d\n", dij());
    }
    return 0;
}

任意两点间最短路径

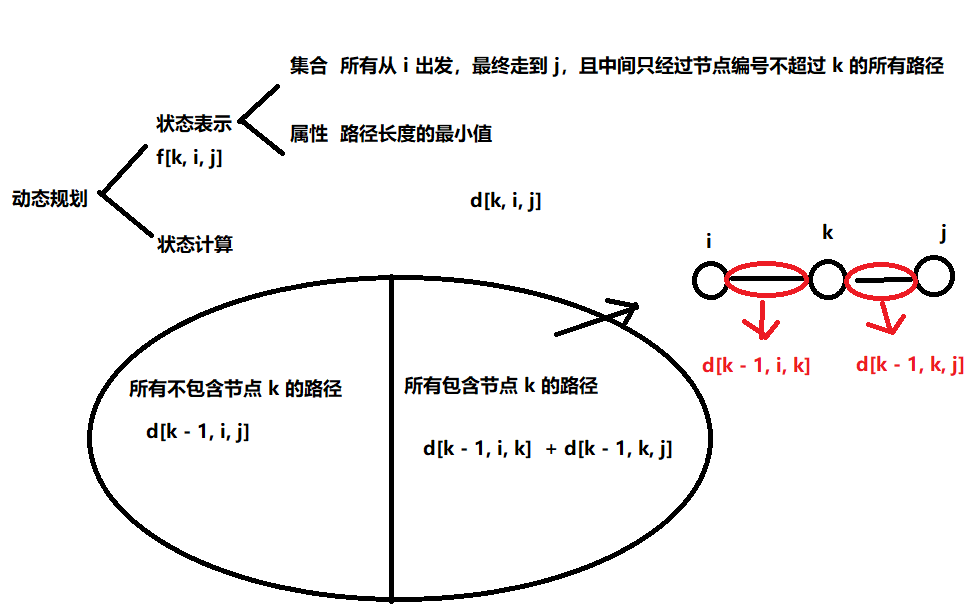
memset(d, 0x3f, sizeof d);
for(int i = 1; i <= n; i ++)    d[i][i] = 0;
for(int k = 1; k <= n; k ++)
    for(int i = 1; i <= n; i ++)
        for(int j = 1; j <= n; j ++)
            f[i][j] = min(f[i][j], f[i][k] + f[k][j]);

Floyd求最短路

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>

using namespace std;

const int N = 210, inf = 0x3f3f3f3f;

int d[N][N], n, m, q;

int main()
{
    cin >> n >> m >> q;
    memset(d, 0x3f ,sizeof d);
    for(int i = 1; i <= n; i ++)    d[i][i] = 0;
    for(int i = 1; i <= m; i ++){
        int a, b, c;
        cin >> a >> b >> c;
        d[a][b] = min(d[a][b], c);
    }

    for(int k = 1; k <= n; k ++)
        for(int i = 1; i <= n; i ++)
            for(int j = 1; j <= n; j ++)
                d[i][j] = min(d[i][j], d[i][k] + d[k][j]);

    while(q --){
        int a, b;
        cin >> a >> b;
        if(d[a][b] > inf / 2)   puts("impossible");
        else    printf("%d\n", d[a][b]);
    }

    return 0;
}

牛的旅行

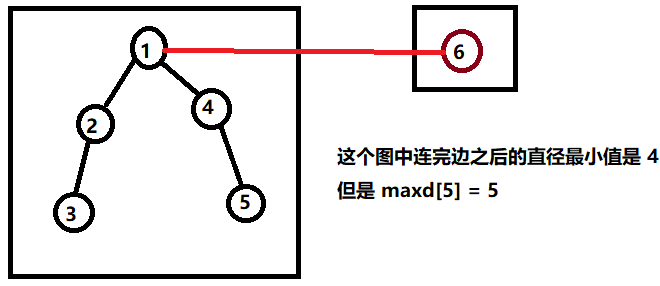
1、用 floyd 算法求出任意两点之间的最短距离

2、求 maxd[i] , 表示和连通的且距离 i 最远的点的距离

3、 情况 1、所有 maxd[i] 的最大值

​ 情况 2、枚举在两个点之间连边(这两个点需满足 d[i, j] == inf), 设 dist 为连边之后的距离，dist = maxd[i] + dis(i, j) + maxd[j], 因需要找到最小的直径，所以需要在枚举的所有情况中找到最小值

4、最后输出需要取 情况 1 和 情况 2 之间的最大值。

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>

using namespace std;
typedef pair < double , double > pdd;
#define x first
#define y second

const int N = 160, inf = 1e18;

pdd q[N];
double d[N][N], maxd[N];
int n;
char g[N][N];

double q_dis(pdd a, pdd b)
{
    double nx = (a.x - b.x);
    double ny = (a.y - b.y);
    return sqrt(nx * nx + ny * ny);
}

int main()
{
    cin >> n;
    for(int i = 0; i < n; i ++){
        cin >> q[i].x >> q[i].y;
    }
    for(int i = 0; i < n; i ++) cin >> g[i];
    for(int i = 0; i < n; i ++)
        for(int j = 0; j < n; j ++){
            if(i == j)  d[i][j] = 0;
            else if(g[i][j] == '1')  d[i][j] = q_dis(q[i], q[j]);
            else    d[i][j] = inf;
        }

    for(int k = 0; k < n; k ++)
        for(int i = 0; i < n; i ++)
            for(int j = 0; j < n; j ++)
                d[i][j] = min(d[i][j], d[i][k] + d[k][j]);

    double res1 = 0.0;
    for(int i = 0; i < n; i ++){
        for(int j = 0; j < n; j ++)
            if(d[i][j] < inf / 2)
                maxd[i] = max(maxd[i], d[i][j]);
        res1 = max(res1, maxd[i]);
    }

    double res2 = inf;
    for(int i = 0; i < n; i ++){
        for(int j = 0; j < n; j ++)
            if(d[i][j] > inf / 2)
                res2 = min(res2, maxd[i] + q_dis(q[i], q[j]) + maxd[j]);
    }
    printf("%.6lf\n", max(res1, res2));

    return 0;
}

传递闭包

给定若干个元素和若干对二元关系，且关系具有传递性。”通过传递性推导出尽量多得元素之间的关系”的问题被称为传递闭包。

建立邻接矩阵 d，其中 d[i, j] = 1 表示 i 与 j 有关系，d[i, j] = 0 表示 i 与 j 没有关系。特别地，d[i, i] 始终为 1。

int main()
{
    cin >> n >> m;
    for(int i = 1; i <= n; i ++)    d[i][i] = 1;
    for(int i = 1; i <= m; i ++){
        int a, b;
        scanf("%d%d", &a, &b);
        d[a][b] = d[b][a] = 1;
    }
    for(int k = 1; k <= n; k ++)
        for(int i = 1; i <= n; i ++)
            for(int j = 1; j <= n; j ++)
                d[i][j] |= d[i][k] & d[k][j];
}

排序

建图：对于每个形如 i < j 的不等式，令 d[i, j] = 1。对于形如 i > j 的不等式，看作 j < i 进行处理。其它情况均是 d[i, j] = 0.

使用 Floyd 算法对 d 进行传递闭包。传递闭包完成后。

若存在变量 i, j，使得 d[i, j] 和 d[j, i] 均为 1，则说明题目中给出的 m 个不等式矛盾。

若存在变量 i, j, 使得 d[i, j] 和 d[j, i] 均为 0，则说明题目中给出的 m 个不等式不能确定每一对变量之间的大小关系。

若对于每对变量 i, j，d[i, j] 和 d[j, i] 有且仅有一个为 1，则说明能确定没对变量之间的大小关系。

#include<iostream>
#include<cstring>
#include<cstdio>
#include<algorithm>

using namespace std;

const int N = 30;

int g[N][N], d[N][N], n, m;
bool st[N];

void floyd()
{
    memcpy(d, g, sizeof g);

    for(int k = 0; k < n; k ++)
        for(int i = 0; i < n; i ++)
            for(int j = 0; j < n; j ++)
                d[i][j] |= d[i][k] & d[k][j];
}

int check()
{
    for(int i = 0; i < n; i ++)
        if(d[i][i])
            return 2;

    for(int i = 0; i < n; i ++)
        for(int j = 0; j < i; j ++)
            if(!d[i][j] && !d[j][i])
                return 0;

    return 1;
}

char get_min()
{
    for(int i = 0; i < n; i ++)
        if(!st[i]){
            int flg = 1;
            for(int j = 0; j < n; j ++){
                if(!st[j] && d[j][i]){
                    flg = 0;
                    break;
                }
            }
            if(flg){
                st[i] = 1;
                return 'A' + i;
            }
        }

}

int main()
{
    while(cin >> n >> m , n || m){
        memset(g, 0, sizeof g);
        int type = 0, t;
        for(int i = 1; i <= m; i ++){
            char str[5];
            cin >> str;
            int a = str[0] - 'A', b = str[2] - 'A';

            if(!type){
                g[a][b] = 1;
                floyd();
                type = check();
                if(type)    t = i;
            }
        }
        if(type == 0)   puts("Sorted sequence cannot be determined.");
        else if(type == 2)  printf("Inconsistency found after %d relations.\n", t);
        else if(type == 1){
            memset(st, 0, sizeof st);
            printf("Sorted sequence determined after %d relations: ", t);
            for(int i = 0; i < n; i ++) printf("%c", get_min());
            printf(".\n");
        }
    }

    return 0;   
}

观光之旅

当外层循环 k 刚开始时，d[i,j] 保存着 “经过编号不超过 k - 1 的节点” 从 i 到 j 的最短路径长度。

于是，min{d[i, j] + g[i, k] + g[k, j]} 就是满足 1、由编号不超过 k 的节点构成。 2、经过节点 k。的最小环长度。

上式中的 i，j 相当于枚举了环上与 k 相邻的两个点。故以上结论显然成立。

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>

using namespace std;

const int N = 110, inf = 0x3f3f3f3f;

int d[N][N], g[N][N], p[N][N];
int a[N], cnt;
int n, m, ans;

void get_path(int l, int r)
{
    if(p[l][r] == 0)    return ;
    int k = p[l][r];
    get_path(l, k);
    a[cnt ++] = k;
    get_path(k, r);
}

int main()
{
    memset(g, 0x3f, sizeof g);
    for(int i = 0; i <= n; i ++)    g[i][i] = 0;
    cin >> n >> m;
    for(int i = 1; i <= m; i ++){
        int a, b, c;
        scanf("%d %d %d", &a, &b, &c);
        g[a][b] = g[b][a] = min(g[a][b], c);
    }

    ans = inf;
    memcpy(d, g, sizeof d);
    for(int k = 1; k <= n; k ++){
        for(int i = 1; i < k; i ++)
            for(int j = i + 1; j < k; j ++){
                if((long long)d[i][j] + g[i][k] + g[k][j] < ans){
                    cnt = 0;
                    ans = d[i][j] + g[i][k] + g[k][j];
                    a[cnt ++] = k;
                    a[cnt ++] = i;
                    get_path(i, j);
                    a[cnt ++] = j;
                }
            }

        for(int i = 1; i <= n; i ++)
            for(int j = 1; j <= n; j ++){
                if(d[i][k] + d[k][j] < d[i][j]){
                    d[i][j] = d[i][k] + d[k][j];
                    p[i][j] = k;
                }
            }
    }

    if(ans == inf)  puts("No solution.");
    else{
        for(int i = 0; i < cnt; i ++)
            printf("%d ", a[i]);
        printf("\n");
    }

    return 0;
}

牛站

设 N * N 的邻接矩阵 A 存储了图中的边。我们可以认为 A[i, j] 表示从 i 到 j 经过一条边的最短路。那么对于方程
$$ \forall i, j \in [1, N], B[i, j] = \min_{1 \le k \le N}{(A[i, k] + A[k, j])} $$
对于 B[i, j] 我们枚举了中转点 k ，从 i 先到 k，然后再到 j 。因此 B[i, j] 表示从 i 到 j 经过两条边的最短路。

然后可以将
$$ B[i, j] == A^2 [i, j] $$
那么矩阵 $A^m$ 可以看成保存了任意两点之间恰好经过 m 条边的最短路。
$$ \forall i,j \in [1, N], (A^{r + m})[i, j] = \min_{i \le k \le N}{((A^r)[i, k] + (A^m)[k, j])} $$
通过这个式子可以看出来，上式其实等价于一个关于 min 与加法运算的广义 “矩阵乘法”。显然，这个广义的 “矩阵乘法” 也满足结合律。因此我们可以用快速幂计算出 $A^N$。

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<map>

using namespace std;

const int N = 210;

int res[N][N], g[N][N], n, m, k, S, E;

void mul(int c[][N], int a[][N], int b[][N])
{
    static int t[N][N];
    memset(t, 0x3f, sizeof t);
    for(int k = 1; k <= n; k ++)
        for(int i = 1; i <= n; i ++)
            for(int j = 1; j <= n; j ++)
                t[i][j] = min(t[i][j], a[i][k] + b[k][j]);
    memcpy(c, t, sizeof t);
}

void qml()
{
    memset(res, 0x3f, sizeof res);
    for(int i = 1; i <= n; i ++)    res[i][i] = 0;

    while(k){
        if(k & 1)   mul(res, res, g);
        mul(g, g, g);
        k >>= 1;
    }
}

int main()
{
    cin >> k >> m >> S >> E;
    memset(g, 0x3f, sizeof g);
    map < int , int > mp;
    mp[S] = ++ n;
    mp[E] = ++ n;
    S = mp[S], E = mp[E];

    for(int i = 1; i <= m; i ++){
        int a, b, c;
        cin >> c >> a >> b;
        if(!mp.count(a))    mp[a] = ++ n;
        if(!mp.count(b))    mp[b] = ++ n;
        a = mp[a], b = mp[b];

        g[a][b] = g[b][a] = min(g[a][b], c);
    }

    qml();

    cout << res[S][E] << endl;

    return 0;
}

负环

负环，又叫负权回路，负权环，指的是一个图中存在一个环，里面包含的边的边权总和<0。在最短路中，如果有负环的话，只要在这个环上不停的走，最短路径就会无限小。

求负环的常用方法，基于 SPFA

(1) 统计每个点入队的次数，如果某个点入队 n 次，则说明存在负环

(2) 统计当前每个点的最短路中所包含的边数，如果某点的最短路所包含的边数大于等于 n ，则也说明存在环。

设 cnt[x] 表示从 1 到 x 的最短路径包含的边数，cnt[1] = 0。当执行更新 d[y] = d[x] + z 时，同时更新 cnt[y] = cnt[x] + 1。此时若发现 cnt[y] >= n ，则图中有负环。

虫洞

模板题

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<queue>

using namespace std;

const int N = 510, M = 5210;

int h[N], ne[M], e[M], w[M], idx;
int d[N], n, m, k, T, cnt[N];
bool st[N];

void add(int a, int b, int c)
{
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++;
}

bool spfa()
{
    memset(d, 0x3f, sizeof d);
    memset(cnt, 0, sizeof cnt);
    memset(st, 0, sizeof st);
    queue < int > q;
    for(int i = 1; i <= n; i ++){
        q.push(i);
        st[i] = 1;
    }
    while(q.size()){
        int t = q.front();q.pop();
        st[t] = 0;

        for(int i = h[t]; ~i; i = ne[i]){
            int v = e[i], z = w[i];
            if(d[v] > d[t] + z){
                d[v] = d[t] + z;
                cnt[v] = cnt[t] + 1;
                if(cnt[v] >= n) return true;
                if(!st[v]){
                    st[v] = 1;
                    q.push(v);
                }
            }
        }
    }
    return false;
}

int main()
{
    cin >> T;
    while(T --){
        memset(h, -1, sizeof h);
        idx = 0;
        cin >> n >> m >> k;
        for(int i = 1; i <= m; i ++){
            int a, b, c;
            scanf("%d %d %d", &a, &b, &c);
            add(a, b, c), add(b, a, c);
        }
        for(int i = 1; i <= k; i ++){
            int a, b, c;
            scanf("%d %d %d", &a, &b, &c);
            add(a, b, -c);
        }

        if(spfa())  puts("YES");
        else    puts("NO");
    }
    return 0;
}

观光奶牛

f[i] 表示每个点的点权，w[i] 表示每个点的边权。我们可以先设节点（1 ~ t）为一个环，假设 $\sum_{i = 1}^{t}{f[i] \over w[i]} \ge mid$ 原问题会变成： 图中是否存在一个环，满足 $\sum_{i = 1} ^ {t} {(f[i] - mid * w[i])} \ge 0$。
$$ \sum_{i = 1}^{t}{f[i] \over w[i]} \ge mid =>\sum_{i = 1} ^ {t}{f[i]} \ge \sum_{i = 1}^{t}{mid * w[i]} =>\sum_{i = 1} ^ {t} {(f[i] - mid * w[i])} \ge 0 $$
可以通过二分答案来找到这个 mid 值，如何检验每个 mid 值，可以通过将图的边权改为 f[x] - mid * w[e] ( 其中边为 x -> y 边权为 w[e])。

如果当前存在一个正环 说明：$\sum_{i = 1} ^ {t} {(f[i] - mid * w[i])} \ge 0$ => mid < ans

如果不存在环 说明： $\sum_{i = 1} ^ {t} {(f[i] - mid * w[i])} < 0$ => mid > ans

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<queue>

using namespace std;

const int N = 1010, M = 5010;

int h[N], ne[M], w[M], e[M], idx;
int cnt[N], n, m, f[N];
double d[N];
bool st[N];

void add(int a, int b, int c)
{
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++;
}

bool spfa(double mid)
{
    memset(d, 0, sizeof d);
    memset(cnt, 0, sizeof cnt);
    memset(st, 0, sizeof st);

    queue < int > q;
    for(int i = 1; i <= n; i ++){
        q.push(i);
        st[i] = 1;
    }
    while(q.size()){
        int t = q.front();q.pop();
        st[t] = 0;

        for(int i = h[t]; ~i; i = ne[i]){
            int v = e[i];
            double z = w[i];
            if(d[v] < d[t] + f[t] - mid * z){
                d[v] = d[t] + f[t] - mid * z;
                cnt[v] = cnt[t] + 1;
                if(cnt[v] >= n) return true;
                if(!st[v])  q.push(v), st[v] = 1;
            }
        }
    }
    return false;
}

int main()
{
    memset(h, -1, sizeof h);
    cin >> n >> m;
    for(int i = 1; i <= n; i ++)    cin >> f[i];
    for(int i = 1; i <= m; i ++){
        int a, b, c;
        cin >> a >> b >> c;
        add(a ,b, c);
    }

    double l = 0, r = 1000.0;
    while(r - l > 1e-4){
        double mid = (l + r) / 2;
        if(spfa(mid))   l = mid;
        else    r = mid;
    }
    printf("%.2lf\n" , l);

    return 0;
}

单词环

建图 ：可以将字符串的前 2 个字母和后 2 个字母 映射成数字（也就是点的编号），字符串的长度就是边权。

然后就是和上一题一样的 0/1 分数规划解法，不过这个题目的点权是 1 。

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>

using namespace std;

const int N = 700, M = 1e5 + 10;

int h[N], ne[M], e[M], w[M], idx;
int n, q[N], cnt[N];
double d[N];
bool st[N];
char str[1010];

void add(int a, int b, int c)
{
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++;
}

bool spfa(double mid)
{
    memset(d, 0, sizeof d);
    memset(st, 0, sizeof st);
    memset(cnt, 0, sizeof cnt);
    int count = 0;
    int hh = 0, tt = 0;
    for(int i = 0; i < 676; i ++){
        q[tt ++] = i;st[i] = 1;
    }
    while(hh != tt){
        int t = q[hh ++];
        if(hh == N) hh = 0;
        st[t] = 0;

        for(int i = h[t]; ~i; i = ne[i]){
            int v = e[i];
            if(d[v] < d[t] + w[i] - mid){
                d[v] = d[t] + w[i] - mid;
                cnt[v] = cnt[t] + 1;
                if( ++ count > 10000)  return true;
                if(cnt[v] >= N) return true;
                if(!st[v]){
                    st[v] = 1;
                    q[tt ++] = v;
                    if(tt == N) tt = 0;
                }
            }
        }
    }
    return false;
}

int main()
{
    while(cin >> n, n){
        memset(h, -1, sizeof h);
        idx = 0;
        for(int i = 1; i <= n; i ++){
            scanf("%s", str);
            int len = strlen(str);
            if(len >= 2){
                int a = (str[0] - 'a') * 26 + str[1] - 'a';
                int b = (str[len - 2] - 'a') * 26 + str[len - 1] - 'a';
                add(a, b, len);
            }
        }

        if(!spfa(0)) puts("No solution");
        else{
            double l = 0, r = 1000.0;
            while(r - l > 1e-4){
                double mid = (l + r) / 2;
                if(spfa(mid))   l = mid;
                else    r = mid;
            }
            printf("%.6lf\n", l);
        }
    }
    return 0;
}