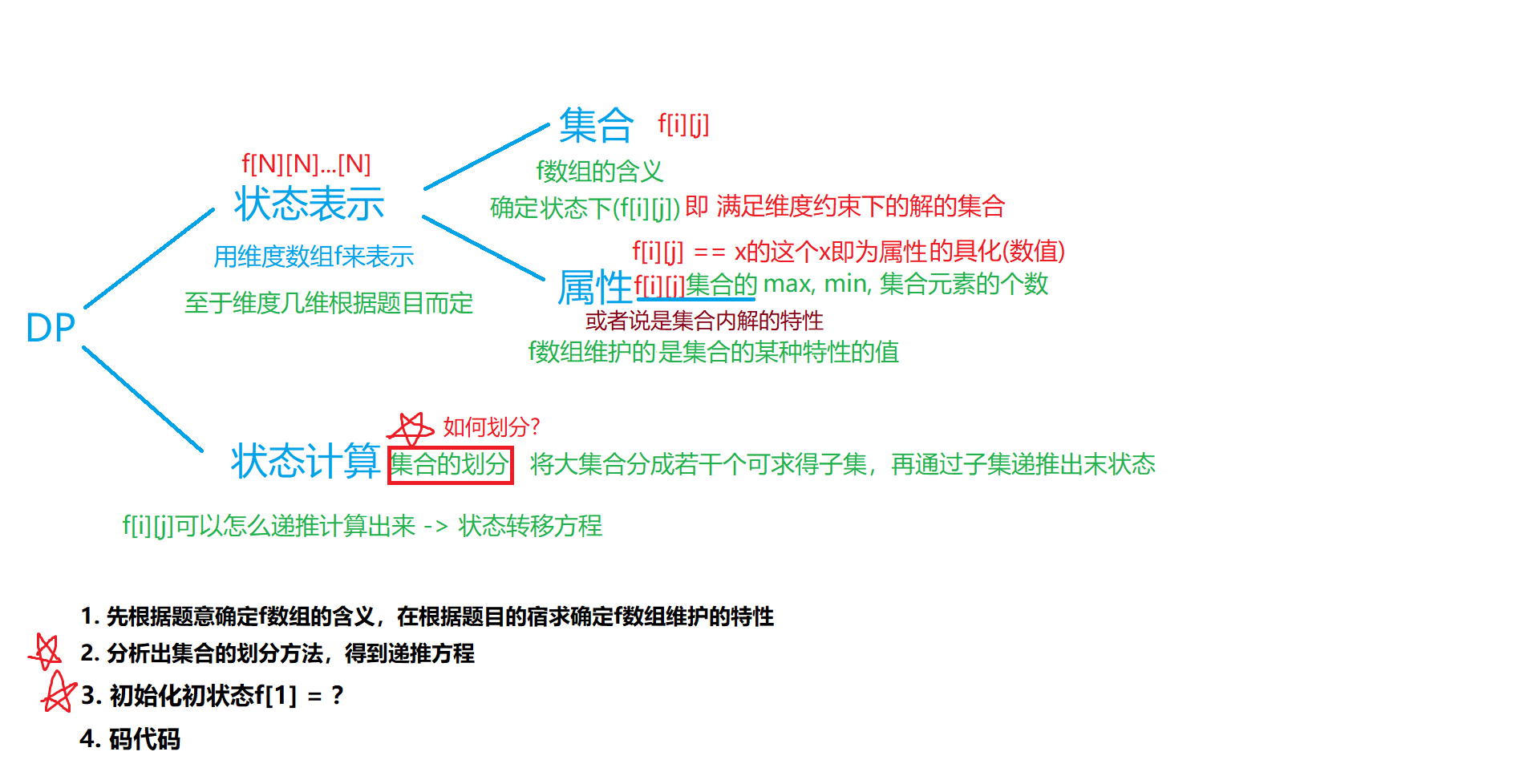
01背包 举例说明 见图解分析法

dp问题的下标
1. 若状态转移方程中有f[i - 1]这种状态, 下标(状态转移那部分代码)尽量从1开始
2. 否则就最好从0开始

dp问题的时间复杂度
状态数量(n^几个约束维度) * 转移状态的时间复杂(状态转移代码的时间复杂度)

dp的集合划分依据 -> 寻找最后一个不同操作 eg. 加不加这个背包, 数字三角形最后一步是由左边还是右边走过来的呀(根据操作的不同来对集合进行划分)
使得划分之后的小集合可以递推求出当前集合, 且最小集合已知