POJ - 2387

起点是 n ，终点是 1，求最短距离。

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<queue>

using namespace std;
typedef pair < int , int > pii;

const int N = 1010, M = 4010;

int h[N], ne[M], e[M], w[M], idx;
int n, m, d[N];
bool st[N];

void add(int a, int b, int c)
{
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++;
}

int dij()
{
    memset(d, 0x3f, sizeof d);
    priority_queue < pii, vector < pii > , greater < pii > > q;
    q.push({0, n});
    d[n] = 0;
    while(q.size()){
        int t = q.top().second;q.pop();
        if(st[t])   continue;
        st[t] = 1;

        for(int i = h[t]; ~i; i = ne[i]){
            int v = e[i], z = w[i];
            if(d[v] > d[t] + z){
                d[v] = d[t] + z;
                q.push({d[v], v});
            }
        }
    }
    return d[1];
}

int main()
{
    memset(h, -1, sizeof h);
    cin >> m >> n;
    for(int i = 1; i <= m; i ++){
        int a, b, c;
        cin >> a >> b >> c;
        add(a, b, c), add(b, a, c);
    }

    printf("%d\n", dij());
    return 0;
}

POJ - 1502

给 2 个点之间的距离（邻接表的形式），求起点到其余每个点的最短路的最大值

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<queue>

using namespace std;
typedef pair < int , int > pii;

const int N = 110, M = 2e5 + 10;

int h[N], ne[M], e[M], w[M], idx;
int n, d[N];
bool st[N];

void add(int a, int b, int c)
{
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++;
}

int stonum(string s)
{
    int len = s.length(), num = 0;
    for(int i = 0; i < len; i ++){
        num = num * 10 + s[i] - '0';
    }
    return num;
}

void dij()
{
    memset(d, 0x3f, sizeof d);
    priority_queue < pii , vector < pii > , greater < pii > > q;
    q.push({0, 1});
    d[1] = 0;
    while(q.size()){
        int t = q.top().second;q.pop();
        if(st[t])   continue;
        st[t] = 1;
        for(int i = h[t]; ~i; i = ne[i]){
            int v = e[i], z = w[i];
            if(d[v] > d[t] + z){
                d[v] = d[t] + z;
                q.push({d[v], v});
            }
        }
    }
}

int main()
{
    memset(h, -1, sizeof h);
    cin >> n;
    string s;
    for(int i = 2; i <= n; i ++)
        for(int j = 1; j < i; j ++){
            cin >> s;
            if(s != "x"){
                int z = stonum(s);
                add(i, j, z), add(j, i, z);
            }
        }

    dij();

    int res = 0;
    for(int i = 1; i <= n; i ++){
        res = max(res, d[i]);
    }
    cout << res << endl;

    return 0;
}

POJ - 3268

单向边，有 2 种情况。

情况 1 ： 从一个起点 k 到其余点的最短路径（单源最短路径算法就可以了）。

情况 2：从其余点前往起点 k 。（需要建一个反向图，就变成了一个单源最短路）。

最后就是情况 1 和情况 2一起加起来取一个最大值。

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<queue>

using namespace std;
typedef pair < int , int > pii;

const int N = 1010, M = 200010;

int h[N], ne[M], e[M], w[M], idx, rh[N];
int n, m, k, d[N], rd[N];
bool st[N];

void add(int h[], int a, int b, int c)
{
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++;
}

void dij()
{
    memset(d, 0x3f, sizeof d);
    memset(st, 0, sizeof st);
    priority_queue < pii, vector < pii > , greater < pii > > q;
    q.push({0, k});
    d[k] = 0;
    while(q.size()){
        int t = q.top().second;q.pop();
        if(st[t])   continue;
        st[t] = 1;
        for(int i = h[t]; ~i; i = ne[i]){
            int v = e[i], z = w[i];
            if(d[v] > d[t] + z){
                d[v] = d[t] + z;
                q.push({d[v], v});
            }
        }
    }
}

void rdij()
{
    memset(rd, 0x3f, sizeof rh);
    memset(st, 0, sizeof st);
    priority_queue < pii, vector < pii > , greater < pii > > q;
    q.push({0, k});
    rd[k] = 0;
    while(q.size()){
        int t = q.top().second;q.pop();
        if(st[t])   continue;
        st[t] = 1;
        for(int i = rh[t]; ~i; i = ne[i]){
            int v = e[i], z = w[i];
            if(rd[v] > rd[t] + z){
                rd[v] = rd[t] + z;
                q.push({rd[v], v});
            }
        }
    }
}

int main()
{
    memset(h, -1, sizeof h);
    memset(rh, -1, sizeof rh);
    cin >> n >> m >> k;
    for(int i = 1; i <= m; i ++){
        int a, b, c;
        cin >> a >> b >> c;
        add(h, a, b, c), add(rh, b, a, c);
    }

    dij();
    rdij();

    int res = 0;
    for(int i = 1; i <= n; i ++){
        res = max(res, d[i] + rd[i]);
    }
    cout << res << endl;

    return 0;
}

POJ - 1511

和上一题一样，这个题目最后是求和

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<queue>

using namespace std;
typedef pair < int , int > pii;

const int N = 1e6 + 10, M = 2e6 + 10;

int h[N], rh[N], ne[M], e[M], w[M], idx;
int n, m, T, d[N], rd[N];
bool st[N];

void add(int h[], int a, int b, int c)
{
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++;
}

void dij()
{
    memset(d, 0x3f, sizeof d);
    memset(st, 0, sizeof st);
    priority_queue < pii, vector < pii > , greater < pii > > q;
    q.push({0, 1});
    d[1] = 0;
    while(q.size()){
        int t = q.top().second;q.pop();
        if(st[t])   continue;
        st[t] = 1;
        for(int i = h[t]; ~i; i = ne[i]){
            int v = e[i], z = w[i];
            if(d[v] > d[t] + z){
                d[v] = d[t] + z;
                q.push({d[v], v});
            }
        }
    }
}

void rdij()
{
    memset(rd, 0x3f, sizeof rh);
    memset(st, 0, sizeof st);
    priority_queue < pii, vector < pii > , greater < pii > > q;
    q.push({0, 1});
    rd[1] = 0;
    while(q.size()){
        int t = q.top().second;q.pop();
        if(st[t])   continue;
        st[t] = 1;
        for(int i = rh[t]; ~i; i = ne[i]){
            int v = e[i], z = w[i];
            if(rd[v] > rd[t] + z){
                rd[v] = rd[t] + z;
                q.push({rd[v], v});
            }
        }
    }
}

int main()
{
    cin >> T;
    while(T --){
        memset(h, -1, sizeof h);
        memset(rh, -1, sizeof rh);
        idx = 0;
        cin >> n >> m;
        for(int i = 1; i <= m; i ++){
            int a, b, c;
            scanf("%d%d%d", &a, &b, &c);
            add(h, a, b, c), add(rh, b, a, c);
        }
        dij();
        rdij();

        long long res = 0;
        for(int i = 1; i <= n; i ++){
            res += d[i] + rd[i];
        }
        cout << res << endl;        
    }

    return 0;
}

POJ - 1797

题目求1到n的所有路径中最小边的权值最大。
改写d数组的含义: d[i] 代表1到i点的所有边中最小值最大的一个。
由于我们用djkstra求最短路的时候会维持一种最短树结构，当我们求某点的d时，指向这个点v的点u的d已经求得，那么如果min(w, d[u]) 中最小的一个还大于我的d[v],那么代表我可以更新这个点的最小值。
以往堆中出来的值是路径最短的一个点，现在堆中出来的值应该是最小值最大的一个点，这样构成的一个拓扑树才能保持这种性质

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<queue>

using namespace std;
typedef pair < int , int > pii;

const int N = 1010, M = 2e6 + 10;

int h[N], ne[M], e[M], w[M], idx;
int n, m, T, d[N];
bool st[N];

void add(int a, int b, int c)
{
    e[idx] = b, w[idx] = c, ne[idx] = h[a] , h[a] = idx ++;
}

void dij()
{
    memset(d, 0, sizeof d);
    memset(st, 0, sizeof st);
    d[1] = 0x3f3f3f3f;
    priority_queue < pii > q;
    q.push({0, 1});
    while(q.size()){
        int t = q.top().second;q.pop();
        if(st[t])   continue;
        st[t] = 1;
        for(int i = h[t]; ~i; i = ne[i]){
            int v = e[i], z = w[i];
            if(d[v] < min(d[t], z)){
                d[v] = min(d[t], z);
                q.push({d[v], v});
            }
        }
    }
}

int main()
{
    int cas = 1;
    cin >> T;
    while(T --){
        memset(h, -1, sizeof h);
        idx = 0;
        cin >> n >> m;
        for(int i = 1; i <= m; i ++){
            int a, b, c;
            scanf("%d%d%d", &a, &b, &c);
            add(a, b, c), add(b, a, c);   
        }

        dij();

        printf("Scenario #%d:\n", cas ++);
        printf("%d\n\n", d[n]);
    }
    return 0;
}

POJ - 2253

题目求 1 到 n 的所有路径中最大边的权值最小。
改写 d 数组的含义: d[i] 代表1到i点的所有边中最大值最小的一个。
由于我们用 djkstra 求最短路的时候会维持一种最短树结构，当我们求某点的 d 时，指向这个点 v 的点 u 的 d 值已经求得，那么如果 max(w, d[u]) 中最大的一个小于我的 d[v] ,那么代表我可以更新这个点的最大值。
以往堆中出来的值是路径最短的一个点，现在堆中出来的值应该是最大值最小的一个点，这样构成的一个拓扑树才能保持这种性质

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<queue>
#include<cmath>

using namespace std;
typedef pair < double , int > pdi;

const int N = 210;

double g[N][N], d[N];
int n, x[N], y[N];
bool st[N];

double get_len(int x1, int y1, int x2, int y2)
{
    return sqrt((x1 - x2) * (x1 - x2) + (y1 - y2) * (y1 - y2));
}

void dij()
{
    for(int i = 1; i <= n; i ++)    d[i] = 1e8;
    memset(st, 0, sizeof st);
    priority_queue < pdi, vector < pdi > , greater < pdi > > q;
    q.push({0, 1});
    d[1] = 0;
    while(q.size()){
        int t = q.top().second;q.pop();
        if(st[t])   continue;
        st[t] = 1;
        for(int i = 1; i <= n; i ++){
            if(d[i] > max(d[t], g[t][i])){
                d[i] = max(d[t], g[t][i]);
                q.push({d[i], i});
            }
        }
    }
}

int main()
{
    int cas = 1;
    while(cin >> n, n){
        memset(g, 0, sizeof g);
        for(int i = 1; i <= n; i ++){
            cin >> x[i] >> y[i];
        }
        for(int i = 1; i <= n; i ++){
            for(int j = i + 1; j <= n; j ++){
                g[i][j] = g[j][i] = get_len(x[i], y[i], x[j], y[j]);
            }
        }

        dij();

        printf("Scenario #%d\n", cas ++);
        printf("Frog Distance = %.3f\n\n", d[2]);
    }
    return 0;
}

HDU - 4725

每个点到其相邻的上下两层都有一条边权为 c 的边，如果我们暴力建边的话，肯定hi超时。所以我们可以为每一层设立一个独立的层级点，该层级点有通向上下相邻层所有点的双向边，权值为c。并且该层点还有通向本层所有点的单向边，边权为 0。（注意不能是双向边）

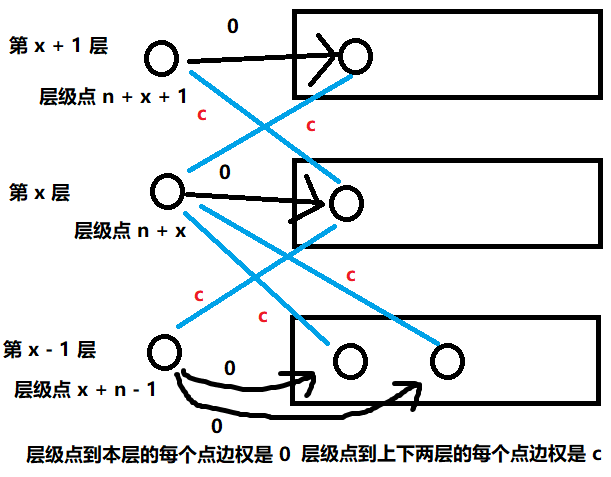
假设每一层有 n 个点，这样就将相邻两层之间的 n * n 条边缩减到了 5 * n 条边，最后加上 m 条双向边。但同时点数就会变成 （n + 层级数）个点。

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<queue>

using namespace std;
typedef pair < int , int > pii;

const int N = 2e5 + 10, M = 7e5 + 10;

int h[N], e[M], ne[M], w[M], idx;
int n, m, T, C, d[N];
bool st[N];

void add(int a, int b, int c)
{
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++;
}

void dij()
{
    memset(st, 0, sizeof st);
    memset(d, 0x3f, sizeof d);
    d[1] = 0;
    priority_queue < pii, vector < pii > , greater < pii > > q;
    q.push({0, 1});
    while(q.size()){
        int t = q.top().second;q.pop();
        if(st[t])   continue;
        st[t] = 1;
        for(int i = h[t]; ~i; i = ne[i]){
            int v = e[i], z = w[i];
            if(d[v] > d[t] + z){
                d[v] = d[t] + z;
                q.push({d[v], v});
            }
        }
    }
}

int main()
{
    int cas = 1;
    cin >> T;
    while(T --){
        memset(h, -1, sizeof h);
        idx = 0;
        cin >> n >> m >> C;
        for(int i = 1; i <= n; i ++){
            int x;
            scanf("%d", &x);
            add(n + x, i, 0);
            add(i, x + n + 1, C), add(x + n + 1, i, C);
            if(x != 1)  add(n + x - 1, i, C), add(i, n + x - 1, C);
        }
        for(int i = 1; i <= m; i ++){
            int a, b, c;
            scanf("%d%d%d", &a, &b, &c);
            add(a, b, c), add(b, a, c); 
        }

        dij();
        int res = d[n];
        if(d[n] == 0x3f3f3f3f)  res = -1;

        printf("Case #%d: %d\n", cas ++, res);
    }
    return 0;
}

POJ - 1847

通向默认路口的路径权值为0，通向其它路口的路径权值为1，然后求解最短路即可。

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<queue>

using namespace std;

const int N = 110, M = 10010;

int h[N], ne[M], e[M], w[M], idx;
int n, m, S, T, d[N];
bool st[N];

void add(int a, int b, int c)
{
    e[idx] = b, w[idx] = c, ne[idx] = h[a] , h[a] = idx ++;
}

void dij()
{
    memset(d, 0x3f, sizeof d);
    queue < int > q;
    q.push(S);
    d[S] = 0;
    st[S] = 1;
    while(q.size()){
        int t = q.front();q.pop();
        st[t] = 0;
        for(int i = h[t]; ~i; i = ne[i]){
            int v = e[i], z = w[i];
            if(d[v] > d[t] + z){
                d[v] = d[t] + z;
                if(!st[v])  q.push(v), st[v] = 1;
            }
        }
    }
}

int main()
{
    memset(h, -1, sizeof h);
    cin >> n >> S >> T;
    for(int i = 1; i <= n; i ++){
        int p;
        cin >> p;
        for(int j = 1; j <= p; j ++){
            int x;
            scanf("%d", &x);
            if(j == 1)  add(i, x, 0);
            else    add(i, x, 1);
        }
    }

    dij();

    if(d[T] == 0x3f3f3f3f)  puts("-1");
    else    printf("%d\n", d[T]);

    return 0;
}

POJ - 2502

先在相邻 2 个站台之间建立一条地铁边。

从起点到所有站台，所有站台到终点都建立一条步行的边。两两站台之间也要建立一条步行的边。

答案输出要四舍五入 int(d + 0.5).

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<queue>
#include<cmath>

using namespace std;

const int N = 210, M = 1e5 + 10;

int h[N], ne[M], e[M], idx;
int n, sx, sy, ex, ey, x[N], y[N];
bool st[N];
double d[N], w[M];

void add(int a, int b, double c)
{
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++;
}

double get_len(int x1, int y1, int x2, int y2, double t)
{
    return sqrt((x1 - x2) * (x1 - x2) + (y1 - y2) * (y1 - y2)) / t / 1000 * 60;
}

void spfa()
{
    queue < int > q;
    for(int i = 0; i <= n; i ++)    d[i] = 1e18;
    q.push(0);
    st[0] = 1;
    d[0] = 0;
    while(q.size()){
        int t = q.front();q.pop();
        st[t] = 0;
        for(int i = h[t]; ~i; i = ne[i]){
            int v = e[i];
            double z = w[i];
            if(d[v] > d[t] + z){
                d[v] = d[t] + z;
                if(!st[v])  st[v] = 1, q.push(v);
            }
        }
    }
}

int main()
{
    memset(h, -1, sizeof h);
    cin >> sx >> sy >> ex >> ey;
    x[n] = sx, y[n ++] = sy;
    int xx, yy;
    while(~scanf("%d%d", &xx, &yy)){
        x[n] = xx, y[n ++] = yy;
        while(~scanf("%d%d", &xx, &yy)){
            if(xx == -1 && yy == -1)    break;
            x[n] = xx, y[n] = yy;
            double dis = get_len(x[n - 1], y[n - 1], x[n], y[n], 40);
            add(n - 1, n, dis), add(n, n - 1, dis);
            n ++;
        }
    }
    x[n] = ex, y[n] = ey;

    for(int i = 0; i <= n; i ++)
        for(int j = 0; j <= n; j ++){
            if(i == j)  continue;
            double dis = get_len(x[i], y[i], x[j], y[j], 10);
            add(i, j, dis), add(j, i, dis);
        }

    spfa();

    printf("%d\n", int(d[n] + 0.5));

    return 0;
}

LightOJ-1074

2个点之间的边为单向边， 权值为(目的点的权 - 源点权)3

由于有负权边。可以用spfa进行求最短路。有负环就返回

#include<iostream>
#include<cstring>
#include<cstdio>
#include<algorithm>
#include<queue>
#include<cmath>

using namespace std;

const int N = 210, M = 40010, inf = 0x3f3f3f3f;

int h[N], ne[M], w[M], e[M], idx;
int n, m, T, d[N], p[N], cnt[N], k;
bool st[N];

void add(int a, int b, int c)
{
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++;
}

void spfa()
{
    memset(d, 0x3f ,sizeof d);
    memset(cnt, 0, sizeof cnt);
    memset(st, 0, sizeof st);
    queue < int > q;
    q.push(1);
    d[1] = 0;
    st[1] = 1;
    while(q.size()){
        int t = q.front();q.pop();
        st[t] = 0;
        for(int i = h[t]; ~i; i = ne[i]){
            int v = e[i], z = w[i];
            if(d[v] > d[t] + z){
                d[v] = d[t] + z;
                cnt[v] = cnt[t] + 1;
                if(cnt[v] >= n) return ;
                if(!st[v])  st[v] = 1, q.push(v);
            }
        }
    }
}

int main()
{
    int cas = 0;
    cin >> T;
    while(T --){
        memset(h, -1, sizeof h);
        idx = 0;
        cin >> n;
        for(int i = 1; i <= n; i ++)    scanf("%d", &p[i]);
        cin >> m;
        for(int i = 1; i <= m; i ++){
            int a, b;
            scanf("%d%d", &a, &b);
            int c = p[b] - p[a];
            add(a, b, c * c * c);
        }

        spfa();

        printf("Case %d:\n", ++cas);
        scanf("%d", &k);
        while (k--) {
            int u;
            scanf("%d", &u);
            if (d[u] < 3 || d[u] > inf / 2) printf("?\n");
            else printf("%d\n", d[u]);
        }
    }
    return 0;
}

POJ - 3259

bell-man 判负环

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<queue>
#include<cstring>
using namespace std;
const int maxn = 1000;
int T, n, m, w, d[maxn];
struct node{
    int u, v, val;
    node(int _u, int _v, int _val){
        u = _u;
        v = _v;
        val = _val;
    }
};
vector < node > g;
bool bellman()
{
    memset(d, 0x3f, sizeof(d));
    d[1] = 0;
    int flg = 0;
    for(int i = 1; i < n; i++){
        flg = 0;
        for(int j = 0; j < g.size(); j++){
            node a = g[j];
            if(d[a.v] > d[a.u] + a.val){
                d[a.v] = d[a.u] + a.val;
                flg = 1;
            }
        }
        if(flg == 0)
            break;
    }
    for(int i = 0; i < g.size(); i++){
        node a = g[i];
        if(d[a.v] > d[a.u] + a.val){
            return true;
        }
    }
    return false;
}
int main()
{
    cin >> T;
    while(T--){
        g.clear();
        cin >> n >> m >> w;
        for(int i = 1; i <= m; i++){
            int x, y, z;
            cin >> x >> y >> z;
            g.push_back(node(x, y, z));
            g.push_back(node(y, x, z));
        }
        for(int i = 1; i <= w; i++){
            int x, y, z;
            cin >> x >> y >> z;
            g.push_back(node(x, y, -z));
        }
        if(bellman()){
            cout << "YES" << endl;
        }else{
            cout << "NO" << endl;
        }
    }
    return 0;
}

POJ - 3660

我们可以根据 A > B 建立一条边，建完图之后可以跑一遍传递闭包。判断一个人是否知道排名，如果知道大于它的（g[i][j]）和小于它的 （g[j][i]）== n - 1 就可以确定一个人的排名

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>

using namespace std;

const int N = 105;

int n, m, g[N][N];

int main()
{
    cin >> n >> m;
    for(int i = 1; i <= m; i ++){
        int a, b;
        cin >> a >> b;
        g[a][b] = 1;
    }

    for(int k = 1; k <= n; k ++)
        for(int i = 1; i <= n; i ++)
            for(int j = 1; j <= n; j ++)
                g[i][j] |= g[i][k] & g[k][j];

    int ans = 0;
    for(int i = 1; i <= n; i ++){
        int cnt = 0;
        for(int j = 1; j <= n; j ++)
            if(g[i][j] || g[j][i])  cnt ++;
        if(cnt == n - 1)    ans ++;
    }

    cout << ans << endl;

    return 0;
}