前言

发现y总 总结得太好了，于是copy y总的总结,补充一点自己的总结

参考资料：
算法基础课
算法提高课

朴素并查集

相关题目：

合并集合 (并查集)
格子游戏 (坐标变换 + 并查集)
程序自动分析 (离散化 + 并查集)

(1)朴素并查集：

    int p[N]; //存储每个点的祖宗节点

    // 返回x的祖宗节点 + 路径压缩
    int find(int x)
    {
        if (p[x] != x) p[x] = find(p[x]);
        return p[x];
    }

    // 初始化，假定节点编号是1~n
    for (int i = 1; i <= n; i ++ ) p[i] = i;

    // 合并a和b所在的两个集合：
    p[find(a)] = find(b);

维护size的并查集

相关题目：

连通块中点的数量 (维护size的并查集)
搭配购买 (01背包 + 并查集)

(2)维护size的并查集：

    int p[N], size[N];
    //p[]存储每个点的祖宗节点, size[]只有祖宗节点的有意义，表示祖宗节点所在集合中的点的数量

    // 返回x的祖宗节点
    int find(int x)
    {
        if (p[x] != x) p[x] = find(p[x]);
        return p[x];
    }

    // 初始化，假定节点编号是1~n
    for (int i = 1; i <= n; i ++ )
    {
        p[i] = i;
        size[i] = 1;
    }

    // 合并a和b所在的两个集合：
    size[find(b)] += size[find(a)];
    p[find(a)] = find(b);

维护到祖宗节点距离的并查集(带权并查集)

相关题目：

银河英雄传说 (维护距离信息的并查集)
奇偶游戏 (前缀和思想简化，离散化 + 带权并查集 / 扩展域)
食物链 (带权并查集 / 扩展域)

(3)维护到祖宗节点距离的并查集：

    int p[N], d[N];
    //p[]存储每个点的祖宗节点, d[x]存储x到p[x]的距离

    // 返回x的祖宗节点
    int find(int x)
    {
        if (p[x] != x)
        {
            int root = find(p[x]);
            d[x] += d[p[x]];
            p[x] = root;
        }
        return p[x];
    }

    // 初始化，假定节点编号是1~n
    for (int i = 1; i <= n; i ++ )
    {
        p[i] = i;
        d[i] = 0;
    }

    // 合并a和b所在的两个集合：
    p[find(a)] = find(b);
    d[find(a)] = distance; // 根据具体问题，初始化find(a)的偏移量

作者：yxc

深度剖析

并查集核心操作 find()

    // 返回x的祖宗节点 + 路径压缩
    int find(int x)
    {
        if (p[x] != x) p[x] = find(p[x]);
        return p[x];
    }

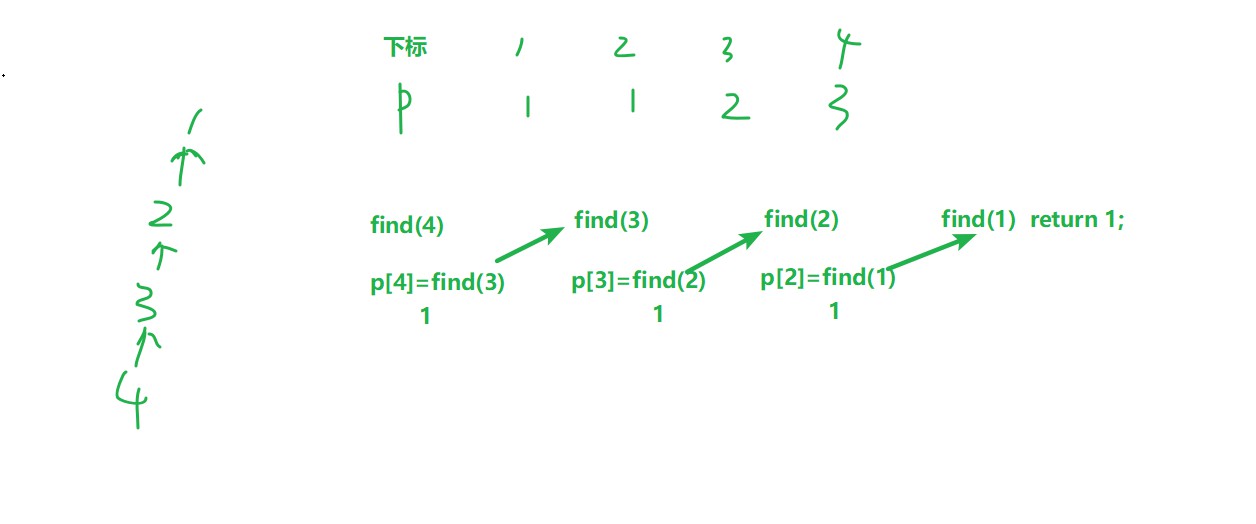
假设我们有如下序列，我们执行一遍find(4),可知在递归返回的时候，这个序列上的数就已经完成了路径压缩，所以能以近乎O(1)的时间查找祖宗结点，实在是妙啊！

关于带权并查集的精华个人总结

只要两个元素在一个集合里面，通过它们与根节点的距离就能知道它们的相对关系

比如食物链一题中，距离% 3 == 0 表示与根节点同类， == 1 表示 被根节点吃， == 2 表示 吃根节点
那么若有 a 与根节点同类， b 也与根节点同类，推出 a 与 b 是同类。

这类带权并查集也可用 并查集扩展域 来做（只要分类不太多的情况下）

此时，p[]数组代表的不是元素，而是 条件