来自算法基础课

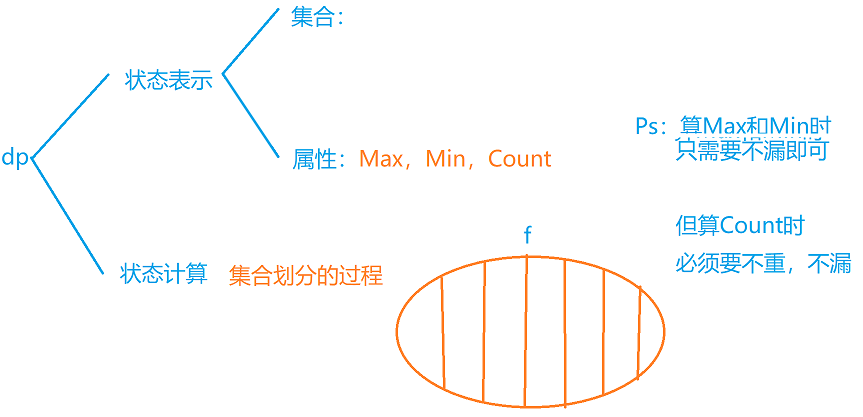
闫氏DP分析法

背包问题

1. 01背包 $O(N \times V)$

for(int i = 1; i <= N; i ++)
    for(int j = V; j >= v[i]; j --)
        f[j] = max(f[j], f[j - v[i]] + w[i]);

2. 完全背包 $O(N \times V)$

for(int i = 1; i <= N; i ++)
    for(int j = v[i]; j <= V; j ++)
        f[j] = max(f[j], f[j - v[i]] + w[i]);

3. 多重背包

(1). 朴素版 $O(V \times N \times s_i)$

for(int i = 1; i <= n; i ++)
    for(int j = 0; j <= m; j ++)
        for(int k = 0; k <= s[i] && k * v[i] <= j; k ++)
            f[i][j] = max(f[i][j], f[i - 1][j - k * v[i]] + k * w[i]);

(2). 二进制优化版 $O(V \times N \times log(s_i))$

while(n --){
    int a, b, s, k = 1;
    scanf("%d %d %d", &a, &b, &s);
    while(s >= k){
        cnt ++;
        v[cnt] = a * k, w[cnt] = b * k;
        s -= k;
        k <<= 1;
    }
    if(s > 0){
        cnt ++;
        v[cnt] = a * s, w[cnt] = b * s;
    }
}
n = cnt;
for(int i = 1; i <= n; i ++)
    for(int j = m; j >= v[i]; j --)
        f[j] = max(f[j], f[j - v[i]] + w[i]);

(3). 单调队列优化版 $O(N \times V)$

for(int i = 1; i <= n; i ++){
    memcpy(g, f, sizeof(f));
    for(int j = 0; j < v[i]; j ++){
        int h = 0, t = -1;
        for(int k = j; k <= m; k += v[i]){
            f[k] = g[k];
            if(h <= t && k - s[i] * v[i] > q[h])
                h ++;
            if(h <= t)
                f[k] = max(f[k], g[q[h]] + (k - q[h]) / v[i] * w[i]); 
            while(h <= t && g[q[t]] - (q[t] - j) / v[i] * w[i] <= g[k] - (k - j) / v[i] * w[i])
                t --;
            q[++ t]=k;
        }
    }
}

4. 分组背包 $O(N \times V \times s_i)$

for(int i = 1; i <= n; i ++)
    for(int j = m; j >= 0; j --)
        for(int k = 1; k <= s[i]; k ++)
            if(j >= v[i][k])
                f[j] = max(f[j], f[j - v[i][k]] + w[i][k]);

线性DP

1. 数字三角形 $O(N^2)$

for(int i = 0; i <= n; i ++)
    for(int j = 0; j <= i + 1; j ++)
        f[i][j] = -INF;
f[1][1] = a[1][1];
for(int i = 2; i <= n; i ++)
    for(int j = 1; j <= i; j ++)
        f[i][j] = max(f[i - 1][j - 1] + a[i][j], f[i - 1][j] + a[i][j]);
int res = -INF;
for(int i = 1; i <= n; i ++)
    res = max(res, f[n][i]);

2. 最长上升子序列

(1). 朴素做法 $O(N^2)$

for(int i = 1; i <= n; i ++){
        f[i] = 1;
        for(int j = 1; j < i; j ++)
            if(a[j] < a[i])
                f[i] = max(f[i], f[j] + 1);
    }
    int res = 0;
    for(int i = 1; i <= n; i ++)
        res = max(res, f[i]);

(2). 优化之后 $O(N \times log(N))$

int len = 0;
q[0] = -INF;
for(int i = 0; i < n; i ++){
    int l = 0, r = len;
    while(l < r){
        int mid = l + r + 1 >> 1;
        if(q[mid] < a[i])
            l = mid;
        else
            r = mid - 1;
    }
    len = max(len, r + 1);
    q[r + 1] = a[i];
}

3. 最长公共子序列 $O(N \times M)$

for(int i = 1; i <= n; i ++)
    for(int j = 1; j <= m; j ++){
        f[i][j] = max(f[i - 1][j], f[i][j - 1]);
        if(a[i] == b[j])
            f[i][j] = max(f[i][j], f[i - 1][j - 1] + 1);
    }

4. 最短编辑距离 $O(N \times M)$

for(int i = 0; i <= m; i ++)
    f[0][i] = i;
for(int i = 0; i <= n; i ++)
    f[i][0] = i;
for(int i = 1; i <= n; i ++)
    for(int j = 1; j <= m; j ++){
        f[i][j] = min(f[i - 1][j] + 1, f[i][j - 1] + 1);
        if(a[i] != b[j])
            f[i][j] = min(f[i][j], f[i - 1][j - 1] + 1);
        else
            f[i][j] = min(f[i][j], f[i - 1][j - 1]);
    }

区间DP

1. 石子合并 $O(N^3)$

for(int len = 2; len <= n; len ++)
    for(int l = 1; l + len - 1 <= n; l ++){
        int r = l + len - 1;
        f[l][r] = INF;
        for(int k = l; k <= r - 1; k ++)
            f[l][r] = min(f[l][r], f[l][k] + f[k + 1][r] + s[r] - s[l - 1]);
    }

计数类DP

1. 把$n$分成若干个正整数相加，一共有多少种方案 $O(N^2)$

f[0][0] = 1;
for(int i = 1; i <= n; i ++)
    for(int j = 1; j <= i; j ++)
        f[i][j] = (f[i - 1][j - 1] + f[i - j][j]) % Mod;
for(int i = 1; i <= n; i ++)
    res = (res + f[n][i]) % Mod;

数位统计DP

1. 统计$a$~$b$中数码$i$出现了几次 $O((log_{10}{n})^3) ≈ O(log_2{n})$

int power_10(int x){
    int s = 1;
    for(int i = 1; i <= x; i ++)
        s *= 10;
    return s;
}

int get(vector<int>& num, int l, int r){
    int s = 0;
    for(int i = l; i >= r; i --)
        s = s * 10 + num[i];
    return s;
}

int count(int n, int x){
    if(!n)
        return 0;
    vector<int> num;
    while(n){
        num.push_back(n % 10);
        n /= 10;
    }
    n = num.size();
    int res = 0;
    for(int i = n - 1 - (x == 0); i >= 0; i --){
        if(i < n - 1){
            res += get(num, n - 1, i + 1) * power_10(i);
            if(x == 0)
                res -= power_10(i);
        }
        if(num[i] == x)
            res += get(num, i - 1, 0) + 1;
        else if(num[i] > x)
            res += power_10(i);
    }
    return res;
}

for(int i = 0; i < 9; i ++)
    ans = count(b, i) - count(a - 1, i)

状态压缩DP

1. 把$N \times M$的棋盘用$1\times2$大小的长方形摆满的方案数 $O(4^N \times N)$

memset(f, 0, sizeof(f));
for(int i = 0; i < 1 << n; i ++){
    int cnt = 0;
    st[i] = true;
    for(int j = 0; j < n; j ++)
        if(i >> j & 1){
            if(cnt & 1)
                st[i] = false;
            cnt = 0;
        }
        else
            cnt ++;
    if(cnt & 1)
        st[i] = false;
}
f[0][0] = 1;
for(int i = 1; i <= m; i ++)
    for(int j = 0; j < 1 << n; j ++)
        for(int k = 0; k < 1 << n; k ++)
            if((j & k) == 0 && st[j | k])
                f[i][j] += f[i - 1][k];

2. 最短Hamilton路径 $O(2^N \times N^2)$

memset(f, 0x3f, sizeof(f));
f[1][0] = 0;
for(int i = 0; i < 1 << n; i ++)
    for(int j = 0; j < n; j ++)
        if(i >> j & 1)
            for(int k = 0; k < n; k ++)
                if((i - (1 << j)) >> k & 1)
                    f[i][j] = min(f[i][j], f[i - (1 << j)][k] + w[k][j]);

f[(1 << n) - 1][n - 1]

树形DP

1. 在不能同时选父节点和子节点的同时，权值最大是多少 $O(N)$

int e[N], ne[N], h[N], idx;
int happy[N], has_father[N];
int f[N][2];
int n;

void add(int a, int b){
    e[idx] = b;
    ne[idx] = h[a];
    h[a] = idx;
    idx ++;
}

void dfs(int u){
    f[u][1] += happy[u];
    for(int i = h[u]; i != -1; i = ne[i]){
        int j = e[i];
        dfs(j);
        f[u][0] += max(f[j][0], f[j][1]);
        f[u][1] += f[j][0];
    }
}

int main(){
    memset(h, -1, sizeof(h));
    input();
    for(int i = 1; i <= n - 1; i ++){
        int a, b;
        scanf("%d %d", &a, &b);
        add(b, a);
        has_father[a] = true;
    }
    int root = 1;
    while(has_father[root])
        root ++;
    dfs(root);
    printf("%d\n", max(f[root][0], f[root][1]));
}

记忆化搜索

1. 求连续的最长下降子序列 $O(N^2)$

int dx[] = {-1, 0, 1, 0}, dy[] = {0, 1, 0, -1};

int dp(int x, int y){
    if(f[x][y] != -1)
        return f[x][y];
    f[x][y] = 1;
    for(int i = 0; i < 4; i ++){
        int a = x + dx[i], b = y + dy[i];
        if(a >= 1 && a <= n && b >= 1 && b <= n && h[a][b] < h[x][y])
            f[x][y] = max(f[x][y], dp(a, b) + 1);
    }
    return f[x][y];
}

int main(){
    input();
    int res = 0;
    memset(f, -1, sizeof(f));
    for(int i = 1; i <= n; i ++)
        for(int j = 1; j <= m; j ++)
            res = max(res, dp(i, j));
    printf("%d\n", res);
}