最小生成树
给定一张边带权的无向图 G = (V, E), n = |V|, m = |E|。由 V 中全部 n 个顶点和 E 中 n - 1 条边构成的无向连通子图被称为 G 的一颗生成树。边的权值之和最小的生成树被称为无向图 G 的最小生成树
1、任意一棵最小生成树一定包含无向图中权值最小的边。
证明:反证法。假设无向图 G = (V, E) 存在一棵最小生成树不包含权值最小的边。设 e = (x, y, z) 是无向图中权值最小的边。把 e 添加到树中,e 会和树上从 x 到 y 的路径一起构成一个环,并且环上其他边的权值都比 z 大。因此,用 e 代替环上的其它任意一条边,会形成一棵权值和更小的生成树,与假设矛盾。
2、给定一张无向图 G = (V, E), n = |V|, m = |E|。从 E 中选出 k < n - 1 条边构成 G 的一个生成森林。若再从剩余的 m - k 条边中选 n - 1 - k 添加到生成森林中,使其成为 G 的生成树,并且选出的边的权值之和最小,则该生成树一定包含这 m - k 条边中连接生成森林的两个不连通的节点的权值最小的边。
Kruskal 算法
Kruskal 算法总是维护无向图的最小生成树。最初,可认为生成森林由零条边构成,每个节点各自构成一颗仅包含一个点的树。在任意时刻,Kruskal 算法从剩余的边中选出一条权值最小的,并且这条边的两个端点属于生成森林中两颗不同的树(不连通),把该边加入生成森林。
1、建立并查集,每个点各自构成一个集合。
2、把所有边按照权值从小到大排序,依次扫描每条边(x, y, z)。
3、若 x, y 属于同一集合(连通),则忽略这条边,继续扫描下一条边。
4、否则,合并 x, y 所在的集合,并把 z 累加到答案中。
5、所有边扫描完成后,第 4 步中处理过的边就构成最小生成树。
struct node{
int a, b, w;
bool operator < (const node & t) const{
return w < t.w;
}
}g[N];
int f[N], n, m;
int find(int x)
{
if(x != f[x]) f[x] = find(f[x]);
return f[x];
}
int main()
{
scanf("%d %d", &n, &m);
for(int i = 0; i < m; i ++){
int a, b, w;
scanf("%d %d %d", &a, &b, &w);
g[i] = {a, b, w};
}
for(int i = 0; i <= n; i ++) f[i] = i;
sort(g, g + m);
int ans = 0;
for(int i = 0; i < m; i ++){
int a = find(g[i].a), b = find(g[i].b), w = g[i].w;
if(a != b) f[a] = b;
else ans += w;
}
cout << ans << endl;
return 0;
}
Prim 算法
Prim 算法总是维护最小生成树的一部分。最初,Prim 算法仅确定 1 号节点属于最小生成树。
在任意时刻,设已经确定属于最小生成树的节点集合为 T,剩余节点集合为 S。Prim 算法找到 $\min_{x \in S,y \in T}{(z)}$,即两个端点分别属于集合 S ,T 的权值最小的边,然后把点 x 从集合 S 中删除,加入到集合 T,并把 z 累加到答案中。
int g[N][N], d[N], n;
bool st[N];
int prim()
{
memset(d, 0x3f, sizeof d);
d[1] = 0;
int res = 0;
for(int i = 1; i <= n; i ++){
int t = -1;
for(int j = 1; j <= n; j ++){
if(!st[j] && (t == -1 || d[j] < d[t]))
t = j;
}
res += d[t];
st[t] = 1;
for(int j = 1; j <= n; j ++){
d[j] = min(d[j], g[t][j]);
}
}
return res;
}
int main()
{
cin >> n;
for(int i = 1; i <= n; i ++)
for(int j = 1; j <= n; j ++)
scanf("%d", &g[i][j]);
int res = prim();
cout << res << endl;
return 0;
}
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 110;
int g[N][N], d[N], n;
bool st[N];
int prim()
{
memset(d, 0x3f, sizeof d);
d[1] = 0;
int res = 0;
for(int i = 1; i <= n; i ++){
int t = -1;
for(int j = 1; j <= n; j ++){
if(!st[j] && (t == -1 || d[j] < d[t]))
t = j;
}
res += d[t];
st[t] = 1;
for(int j = 1; j <= n; j ++){
d[j] = min(d[j], g[t][j]);
}
}
return res;
}
int main()
{
cin >> n;
for(int i = 1; i <= n; i ++)
for(int j = 1; j <= n; j ++)
scanf("%d", &g[i][j]);
int res = prim();
cout << res << endl;
return 0;
}
删除一些边,需要满足1、原图依然是连通的。2、输出的边权和最大。所以就相当于对原图求一遍最小生成树,答案就是所有边权和减去最小生成树的权值和。因为题目说的是森林,所以用kruskal 算法更方便。
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 110;
struct node{
int a, b, c;
bool operator < (node t) const{
return c < t.c;
}
} g[210];
int f[N], n, m;
int find(int x)
{
if(x != f[x]) f[x] = find(f[x]);
return f[x];
}
int main()
{
cin >> n >> m;
for(int i = 1; i <= n; i ++){
f[i] = i;
}
for(int i = 1; i <= m; i ++){
int a, b, c;
cin >> a >> b >> c;
g[i] = {a, b, c};
}
sort(g + 1, g + 1 + m);
int res = 0;
for(int i = 1; i <= m; i ++){
int a = g[i].a, b = g[i].b, w = g[i].c;
a = find(a), b = find(b);
if(a != b) f[a] = b;
else res += w;
}
cout << res << endl;
return 0;
}
Kruskal 算法
1、将所有边从小到大排序
2、从小到大依次枚举每条边,a, b, c。
如果 a 和 b 已经连通,那么直接 pass。 如果 a 和 b 不连通,那么就将当前边选出来。
最后在所有的选出来的边中选择最大值
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 310, M = 8010;
struct node{
int a, b, c;
bool operator < (node t) const{
return c < t.c;
}
}g[M];
int f[N], n, m;
int find(int x)
{
if(x != f[x]) f[x] = find(f[x]);
return f[x];
}
int main()
{
cin >> n >> m;
for(int i = 1; i <= n; i ++) f[i] = i;
for(int i = 1; i <= m; i ++){
int a, b, c;
cin >> a >> b >> c;
g[i] = {a, b, c};
}
sort(g + 1, g + 1 + m);
int res;
for(int i = 1; i <= m; i ++){
int a = g[i].a, b = g[i].b, w = g[i].c;
a = find(a), b = find(b);
if(a != b){
f[a] = b;
res = w;
}
}
printf("%d %d\n", n - 1, res);
return 0;
}
将所有的必选边加入之后,会形成一个森林,可以通过缩点将森林的每一棵树看成一个点,然后就可以看成最小生成树,对所有非必选边进行求最小生成树。
1、将所有必选边加到并查集中(也相当于是一个缩点的过程)
2、将所有非必选边从小到大排序
3、从小到大依次枚举每一条非必选边
如果 a 和 b 已经连通,直接 pass 如果 a 和 b 不连通,那么就将当前边加入到最小生成树中。
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 2010, M = 1e4 + 10;
struct node{
int a, b, c;
bool operator < (node t) const{
return c < t.c;
}
}g[M];
int f[N], n, m;
int find(int x)
{
if(x != f[x]) f[x] = find(f[x]);
return f[x];
}
int main()
{
cin >> n >> m;
for(int i = 1; i <= n; i ++) f[i] = i;
int res = 0, k = 0;
for(int i = 1; i <= m; i ++){
int a, b, c, d;
cin >> d >> a >> b >> c;
if(d == 1){
a = find(a), b = find(b);
f[a] = b;
res += c;
}
else g[k ++] = {a, b, c};
}
sort(g, g + k);
for(int i = 0; i < k; i ++){
int a = g[i].a, b = g[i].b, w = g[i].c;
a = find(a), b = find(b);
if(a != b){
res += w;
f[a] = b;
}
}
cout << res << endl;
return 0;
}
将题目给定的边先连起来
然后先遍历纵向的边,然后遍历横向的边(先遍历长度为 1 的边,然后遍历长度为 2 的边)
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 1e3 + 10;
int f[N * N], n, m;
int find(int x)
{
if(x != f[x]) f[x] = find(f[x]);
return f[x];
}
int main()
{
cin >> n >> m;
for(int i = 1; i <= n * m; i ++ ) f[i] = i;
int a, b, c, d;
while(~scanf("%d%d%d%d", &a, &b, &c, &d)){
int e = (a - 1) * m + b, g = (c - 1) * m + d;
f[find(e)] = find(g);
}
int res = 0;
for(int i = 1; i < n; i ++)
for(int j = 1; j <= m; j ++){
int a = (i - 1) * m + j, b = i * m + j;
a = find(a), b = find(b);
if(a != b) f[a] = b, res += 1;
}
for(int i = 1; i <= n; i ++)
for(int j = 1; j < m; j ++){
int a = (i - 1) * m + j, b = (i - 1) * m + j + 1;
a = find(a), b = find(b);
if(a != b) f[a] = b, res += 2;
}
cout << res << endl;
return 0;
}
为了保证电力的供应,小 FF 想到了两种办法:
- 在矿井 i 上建立一个发电站,费用为 $v_i$(发电站的输出功率可以供给任意多个矿井)。
- 将这口矿井 i 与另外的已经有电力供应的矿井 j 之间建立电网,费用为 $p_{i,j}$。
可以建立一个超级源点,该超级源点向其余每个点连一条边,边权为每个点的点权。该超级源点可以理解为超级电力发电站(此时的情况1 转换成了超级源点向该点建边来提供电力,也即转换成了情况 2)。
然后可以在这 n + 1 个点之间建立最小生成树,也即情况 2 的解法。
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 310;
int g[N][N], n, d[N];
bool st[N];
int prim()
{
int res = 0;
memset(d, 0x3f, sizeof d);
d[0] = 0;
for(int i = 0; i <= n; i ++){
int t = -1;
for(int j = 0; j <= n; j ++)
if(!st[j] && (t == -1 || d[j] < d[t]))
t = j;
st[t] = 1;
res += d[t];
for(int j = 0; j <= n; j ++)
d[j] = min(d[j], g[t][j]);
}
return res;
}
int main()
{
cin >> n;
for(int i = 1; i <= n; i ++){
int x;
scanf("%d", &x);
g[0][i] = g[i][0] = x;
}
for(int i = 1; i <= n; i ++)
for(int j = 1; j <= n; j ++)
scanf("%d", &g[i][j]);
int res = prim();
cout << res << endl;
return 0;
}
首先肯定是建最小生成树的,然后可以将最小生成树中的 k - 1 条边的边权值变为 0 。然后答案求的是剩下的边权最大值
假设给定一个 d 值,将长度小于等于 d 值的边连上之后,会形成 m 个连通块,这个时候则需要 m 个卫星设备。
=>找到一个最小的 d 值,使得将所有权值大于 d 的边删去之后,整个图形的连通块的个数不超过 k(可以用二分加判断连通块个数来做)
=>找到一个最小的 d 值,使得将所有权值小于 d 的边添加上之后,整个图形的连通块的个数不超过 k 。
Kruskal 算法
1、先将所有边按边权从小到大排序
2、从小到大扫描所有边,依次将没有合并的点合并,同时连通块个数减一
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
using namespace std;
typedef pair < int , int > pii;
#define x first
#define y second
const int N = 510, M = N * N / 2;
int n, k, f[N];
struct node{
int a, b;
double c;
bool operator < (node t) const{
return c < t.c;
}
}g[M];
pii q[N];
double q_dis(pii a, pii b)
{
int x = a.x - b.x;
int y = a.y - b.y;
return sqrt(x * x + y * y);
}
int find(int x)
{
if(x != f[x]) f[x] = find(f[x]);
return f[x];
}
int main()
{
cin >> n >> k;
for(int i = 1; i <= n; i ++){
cin >> q[i].x >> q[i].y;
f[i] = i;
}
int m = 0;
for(int i = 1; i <= n; i ++)
for(int j = i + 1; j <= n; j ++){
g[m ++] = {i, j, q_dis(q[i], q[j])};
}
sort(g, g + m);
int cnt = n;
double res;
for(int i = 0; i < m; i ++){
if(cnt <= k) break;
int a = g[i].a, b = g[i].b;
double w = g[i].c;
a = find(a), b = find(b);
if(a != b){
f[a] = b;
cnt --;
res = w;
}
}
printf("%.2lf\n", res);
return 0;
}
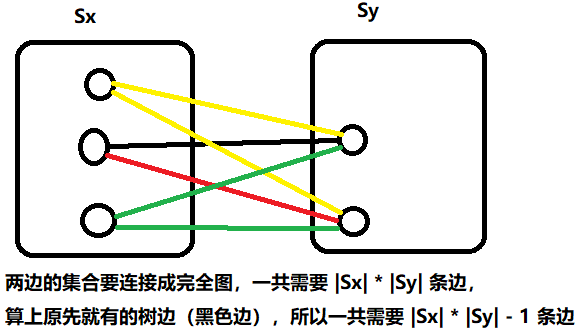
n 个节点的树有 n - 1 条边。把这 n - 1 条边按照权值从小到大排序,依次扫描每条边。设当前扫描到边(x, y, z), x 所在的并查集为 $S_x$,y 所在的并查集为 $S_y$,此时应该合并 $S_x$ 与 $S_y$ 。合并后的集合 $S_x \cup S_y$ 构成一棵树的结构。$\forall u \in S_x, v \in S_y$,若 $(u, v) \ne (x, y)$,则在最终的完全图中,我们肯定需要在 (u, v) 之间增加一条边。于是,无向边 (u, v) 、$S_x$ 中从 u 到 x 的路径、无向边 (x, y) 以及 $S_y$ 中从 v 到 y 的路径共同构成一个环
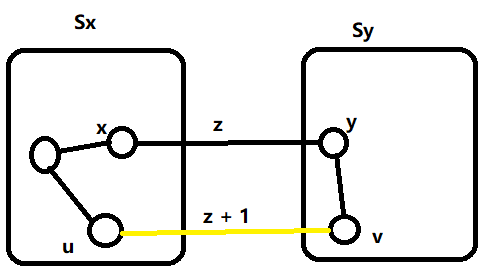
为了保证 (x, y) 一定在最小生成树中,就必须让 (x, y) 是连接集合 $S_x$ 与 $S_y$ 的权值最小的边(否则就可以用 (u, v) 替换 (x, y) )因此,(u, v) 的边权应该定位 z + 1。
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 6010;
struct node{
int a, b, c;
bool operator < (node t) const{
return c < t.c;
}
}g[N];
int f[N], s[N], n, T;
int find(int x)
{
if(x != f[x]) f[x] = find(f[x]);
return f[x];
}
int main()
{
cin >> T;
while(T --){
cin >> n;
for(int i = 1; i < n; i ++){
int a, b, c;
cin >> a >> b >> c;
g[i] = {a, b, c};
}
for(int i = 1; i <= n; i ++)
f[i] = i, s[i] = 1;
sort(g + 1, g + n);
long long res = 0;
for(int i = 1; i < n; i ++){
int a = find(g[i].a), b = find(g[i].b), w = g[i].c;
if(a != b){
f[a] = b;
res += (long long)(w + 1) * (s[a] * s[b] - 1);
s[b] += s[a];
}
}
cout << res << endl;
}
return 0;
}
设G = (V, E)是连通的无向图,T是图G的一个最小生成树.如果有另外一棵树T1,T1 ≠ T,满足不存在树T’,T’ ≠ T,w(T’) < w(T1),则称T1是图G的次小生成树.
先求最小生成树,然后依次枚举非树边,然后将该边加入树中,同时从树中去掉一条边,使得最终的图仍是一棵树。
设 T 为图 G 的一颗生成树,对于非树边 a 和树边 b,插入边 a,并删去边 b 的操作记为(+a,-b)。如果 T + a - b 之后,仍然是一颗生成树,称 (+a, -b) 是 T 的一个可行操作。称由 T 进行一次可行变换所得到的新的生成树集合称为 T 的邻集。
求严格次小生成树时,不能只预处理两点之间最大的树边,因为当最大树边和当前枚举的非树边长度相同时,就不能替换了,但此时却可以替换长度次大的树边。因此还需同时预处理出长度次大的树边。
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 510, M = 1e4 + 10;
struct node{
int a, b, w;
bool f;
bool operator < (node t) const{
return w < t.w;
}
}g[M];
int f[N], n, m, d[N][N], d1[N][N];
int h[N], ne[N * 2], e[N * 2], w[N * 2], idx;
void add(int a, int b, int c)
{
e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++;
}
int find(int x)
{
if(x != f[x]) f[x] = find(f[x]);
return f[x];
}
void dfs(int u, int fa, int mx, int mx1, int d[], int d1[])
{
d[u] = mx, d1[u] = mx1;
for(int i = h[u]; ~i; i = ne[i]){
int t = e[i], z = w[i];
if(t != fa){
int nmx = mx, nmx1 = mx1;
if(z > nmx) nmx1 = nmx, nmx = z;
else if(z < nmx && z > nmx1) nmx1 = z;
dfs(t, u, nmx, nmx1, d, d1);
}
}
}
int main()
{
memset(h, -1, sizeof h);
cin >> n >> m;
for(int i = 1; i <= n; i ++) f[i] = i;
for(int i = 1; i <= m; i ++){
int a, b, c;
cin >> a >> b >> c;
g[i] = {a, b, c};
}
sort(g + 1, g + 1 + m);
long long res = 0;
for(int i = 1; i <= m; i ++){
int a = g[i].a, b = g[i].b, w = g[i].w;
int fa = find(a), fb = find(b);
if(fa != fb){
f[fa] = fb;
add(a, b, w);
add(b, a, w);
res += w;
g[i].f = 1;
}
}
for(int i = 1; i <= n; i ++) dfs(i, -1, -1e9, -1e9, d[i], d1[i]);
long long sum = 1e18;
for(int i = 1; i <= m; i ++){
if(!g[i].f){
int a = g[i].a, b = g[i].b, w = g[i].w;
long long t;
if(w > d[a][b]) t = res + w - d[a][b];
else if(w > d1[a][b]) t = res + w - d1[a][b];
sum = min(sum, t);
}
}
cout << sum << endl;
return 0;
}

