前言

动态规划为什么快呢？ – 用一个状态表示一堆方案的最值 –yxc
DP：一个值代表一类搜索
闫式DP分析法：从集合的角度，状态计算从“最后一步”考虑
参考资料：算法基础课，算法提高课

背包问题分类

01背包 $ O(nm) $

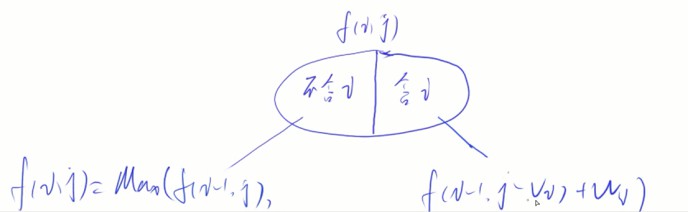
状态计算：不选第i个物品和选第i个物品

#include <iostream>

using namespace std;

const int N = 1010;

int n,m;
int v[N], w[N];
int f[N][N];

int main()
{
    cin>>n>>m;

    for (int i = 1; i <= n;i ++ ) cin >> v[i] >> w[i];

    for (int i = 1; i <= n; i ++ )
        for (int j = 1; j <= m; j ++ )
        {
            f[i][j] = f[i-1][j];
            if (j >= v[i]) f[i][j] = max(f[i][j], f[i - 1][j - v[i]] + w[i]);
        }

    cout << f[n][m] << endl;

    return 0;
}

优化空间之后的写法(体积从大到小枚举)

这个滚动数组优化我还是没搞明白，只能先记个结论这样子，与下文完全背包区别

#include <iostream>

using namespace std;

const int N = 1010;

int n,m;
int v[N], w[N];
//int f[N][N];
int f[N];

int main()
{
    cin>>n>>m;

    for (int i = 1; i <= n;i ++ ) cin >> v[i] >> w[i];

    for (int i = 1; i <= n; i ++ )
        for (int j = m; j >= v[i]; j -- )
          f[j] = max(f[j], f[j - v[i]] + w[i]);

    //cout << f[n][m] << endl;
    cout<<f[m]<<endl;

    return 0;
}

完全背包$O(n ^ 3)$

第i个物品选多少个

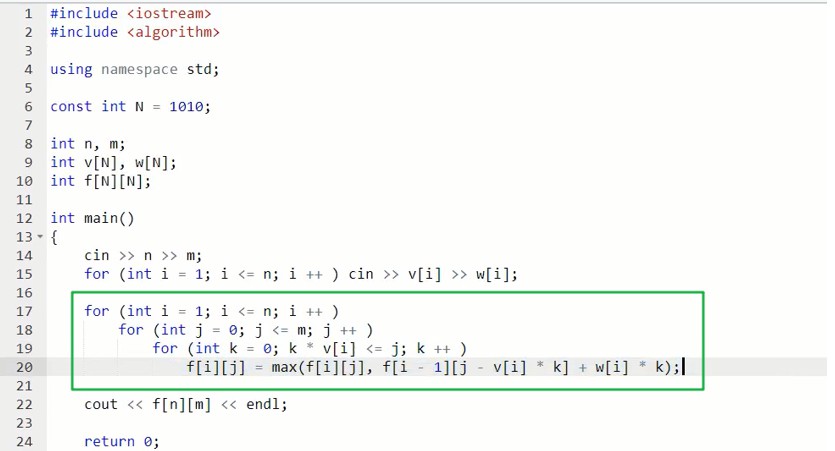
优化 $O(n ^ 2)$

优化空间的写法（体积从小到大）

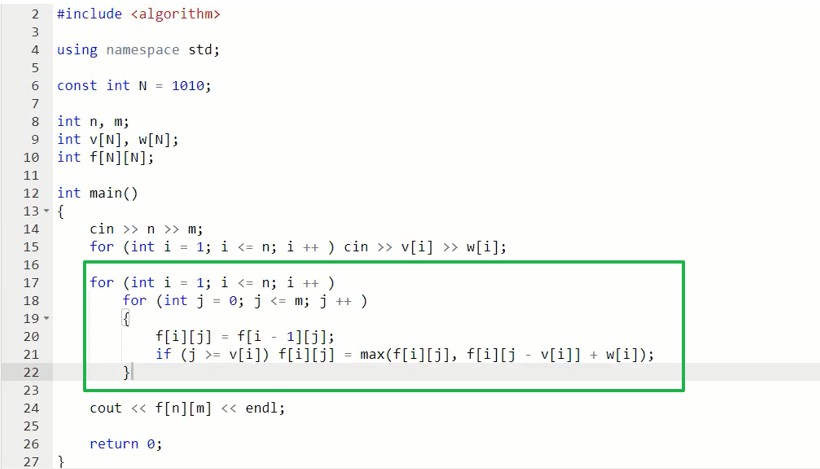
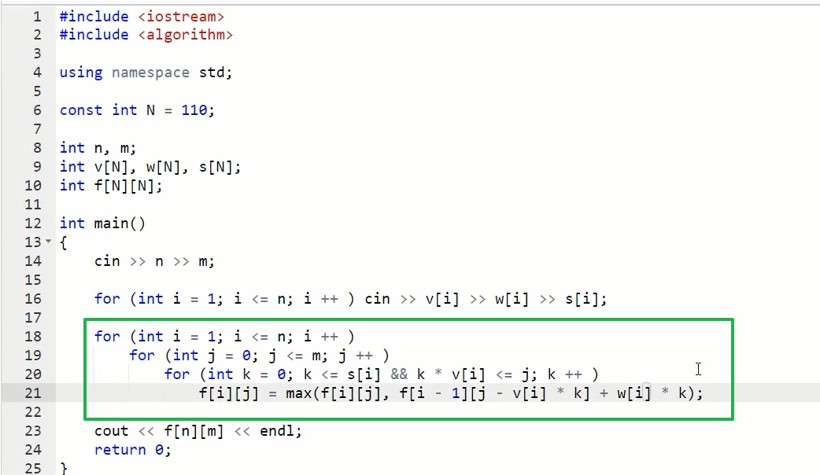
多重背包$O(NVS)$

第i个物品选k个

多重背包二进制优化$O(NVlog(S))$

核心思想：
转换为01背包，把s拆成log(s)份

#include <iostream>

using namespace std;

const int N = 12010, M = 2010; // N = 2000 * log(2000)
// 核心：利用二进制把s份拆成 log(s) 份

int n,m;
int v[N], w[N];
int f[M];

int main()
{
    cin >> n >> m;

    int cnt = 0;
    for(int i=1;i<=n;i++)
    {
        int a,b,s;
        cin >> a >> b >> s;
        int k = 1;
        while(k <= s)
        {
            cnt ++ ;
            v[cnt] = a * k;
            w[cnt] = b * k;
            s -= k;
            k *= 2;
        }
        if(s > 0) // 剩下的凑成一组
        {
            cnt ++ ;
            v[cnt] = a * s;
            w[cnt] = b * s;
        }
    }

    n = cnt; // 总共有cnt组，做一遍01背包

    for(int i=1;i<=n;i++)
        for(int j = m; j >= v[i]; j --)
            f[j] = max(f[j],f[j - v[i]] + w[i]);

    cout<<f[m]<<endl;

    return 0;
}

分组背包 $O(NVS)$

第i组选哪个

#include <iostream>

using namespace std;

const int N = 110;

int n,m;
int v[N][N], w[N][N], s[N];
int f[N];

int main()
{
    cin >> n >> m;

    for(int i =1;i<=n;i++)
    {
        cin >> s[i];
        for(int j = 0; j < s[i];j ++)
            cin >> v[i][j] >> w[i][j];
    }

    for(int i=1;i<=n;i++)
        for(int j=m;j >=0 ;j --)
            for(int k =0;k<s[i];k ++)
                if(v[i][k] <= j)
                    f[j] = max(f[j],f[j-v[i][k]] + w[i][k]);

    cout<<f[m]<<endl;

    return 0;
}