差分约束

emmm… 先感谢 y总 lyd 二助 xnuohz 等大佬

1、差分约束系统

是求解一组特殊的 N 元一次不等式组。它包含了 N 个变量 $x_1$ ~ $x_n$和 M 个约束条件，其中每个约束条件形如,
$$ x_j - x_i <= c_k(i,j∈[1,n],k∈[1,m]) $$
(其中 $c_k$ 是常数，可以是负数或者正数) 则称其为差分约束系统

通俗一点地说，差分约束系统就是一些不等式的组，而我们的目标是通过给定的约束不等式组求出最大值或者最小值或者差分约束系统是否有解。
$$ \left\\{ \begin{array}{c} x_1 - x_0 <= 2 \\\ x_2 - x_0 <= 7 \\\ x_3 - x_0 <= 8 \\\ x_2 - x_1 <= 3 \\\ x_3 - x_2 <= 2 \end{array} \right. $$
如果要求出$x_3-x_0$的最大值的话，叠加不等式可以推导出$x_3-x_0<=7$,最大值即为7。

2、求解

(1) 先将每个不等式 $x_i <= x_j + c_k$ 转化成一条从 $x_j$ 走到 $x _i$ ，长度为 $c_k$ 的一条边。

三角不等式

$$ \left\\{ \begin{array}{} B - A <= c \\\ C - B <= a \\\ C - A <= b \end{array} \right. => \left\\{ \begin{array}{c} C - A <= a + c \\\ C - A <= b \end{array} \right. => \left\\{ \begin{array}{c} C - A <= \min(a + c, b) \end{array} \right. $$

我们可以将大写字母看成点，B <= A + c 看成 A 向 B 建一条边权为 c 的边

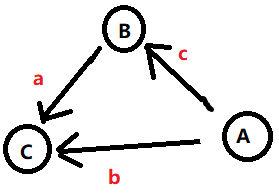
通过建图可以发现 C - A 的最大值就是 A 到 C 的最短路径长度。

同样我们可以对差分约束系统的每个约束条件 $x_i - x_j \leq c_k$ 可以变形成为 $x_ \leq x_j + c_k$。这与单源最短路径问题中的三角形不等式 d[v] <= d[t] + z 非常相似。因此可以把每个变量 $x_i$ 看作有向图中的一个节点 i，对于每个约束条件 $x_i - x_j \leq c_k$，从节点 $x_j$ 向节点 $x_i$ 连一条长度为 $c_k$ 的边。

比如一开始的差分约束系统可以建图为，然后在这个图上求一次最短路，就可以求出 $x_0 ~ x_3$ 的最短路径，也就是 $x_3 - x_0$ 的最大值。

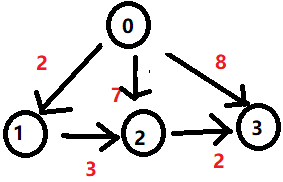
因此，对三角不等式加以推广，变量 n 个，不等式 m 个，要求$x_n-x_1$的最大值，便就是求取建图后的最短路。

同样地，如果要求取差分约束系统中$x_n-x_1$的最小值，便是求取建图后的最长路。

但是当图中如果存在负环或者正环的情况下，就会出现无解的情况（因为这种情况下，不等式组会出现矛盾现象）。

(2) 找一个超级源点，使得该源点一定可以遍历所有边。

因为图不一定是全连通的，所以需要找一个源点，一定可以走到所有边，这样才能保证找到可行解。

同时因为如果 ${a_1, a_2, a_3 …a_n} $ 是一组解，那么对于任何常数 $\Delta$ ,${a_1 + \Delta , … , a_n + \Delta}$ 也是一组解，所以可以对于每一个变量建立一个 $X_i - X_0 \leq \Delta$ 这样的约束条件,这样一来就多了 n 个形如 $X_i - X_0 \leq 0$ 的约束条件，也就是增加一个超级源点，向每一个点连一条长度为 0 的边。

所以可以设 d[0] = 0, 以 0 为起点求单源最短路。$X_i = d[i]$ 就是差分约束的一组解。

(3) 从源点求一遍单源最短路

结果 1：如果存在负环，则原不等式组无解

结果 2：如果没有负环，则 d[i] 就是差分约束的一组解。

解的存在性
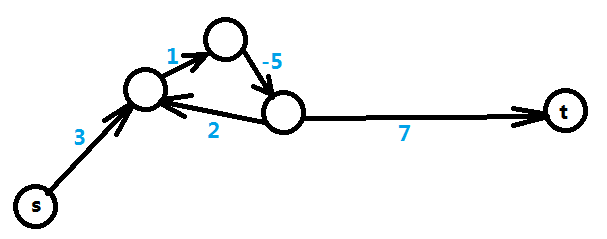
，先来看负权圈的情况，下图为5个变量5个不等式转化后的图，需要求得是X[t] - X[s]的最大值，可以转化成求s到t的最短路，但是路径中出现负权圈，则表示最短路无限小，即不存在最短路，那么在不等式上的表现即X[t] - X[s] <= T中的T无限小，得出的结论就是 X[t] - X[s]的最大值不存在

再来看另一种情况，即从起点s无法到达t的情况，如图，表明X[t]和X[s]之间并没有约束关系，这种情况下X[t] - X[s]的最大值是无限大，这就表明了X[t]和X[s]的取值有无限多种。

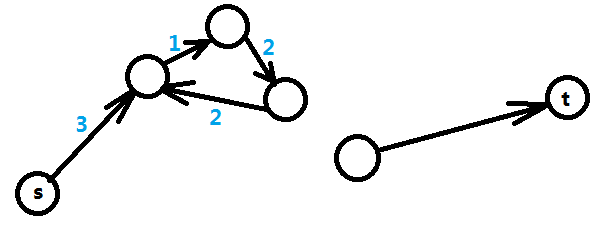
在实际问题中这两种情况会让你给出不同的输出。综上所述，差分约束系统的解有三种情况：1、有解；2、无解；3、无限多解；

最长路 <-> 大于关系
最短路 <-> 小于关系

糖果

1、将每个不等式转化成一条边
$$ \left\\{ \begin{array}{} 操作 1 => A = B <=> A \ge B , B \ge A \\\ 操作 2 => A < B <=> B \ge A + 1 \\\ 操作 3 => A \ge B <=> A \ge B \\\ 操作 4 => A > B <=> A \ge B + 1 \\\ 操作 5 => A \leq B <=> B \ge A \end{array} \right. $$
2、只能建立一个超级源点 0 并且因为每一个人都需要分得一个糖果，所以需要建立 n 个不等式 $X_i - X_0 \ge 1$。

3、从超级源点开始求一遍最长路（因为是大于关系）

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>

using namespace std;

const int N = 1e5 + 10, M = 3e5 + 10;

int h[N], ne[M], e[M], w[M], idx;
int n, m, cnt[N], q[N];
long long d[N];
bool st[N];

void add(int a, int b, int c)
{
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++;
}

bool spfa()
{
    int tt = 1;
    memset(d, -0x3f, sizeof d);
    q[0] = 0;
    d[0] = 0;
    st[0] = 1;

    while(tt != 0){
        int t = q[ -- tt];
        st[t] = 0;

        for(int i = h[t]; ~i; i = ne[i]){
            int v = e[i];
            if(d[v] < d[t] + w[i]){
                d[v] = d[t] + w[i];
                cnt[v] = cnt[t] + 1;
                if(cnt[v] >= n + 1) return true;
                if(!st[v]){
                    st[v] = 1;
                    q[tt ++] = v;
                }
            }
        }
    }
    return false;
}

int main()
{
    memset(h, -1, sizeof h);
    cin >> n >> m;
    for(int i = 1; i <= m; i ++){
        int k, a, b;
        scanf("%d%d%d", &k, &a, &b);
        if(k == 1)  add(a, b, 0), add(b, a, 0);
        else if(k == 2) add(a, b, 1);
        else if(k == 3) add(b, a, 0);
        else if(k == 4) add(b, a, 1);
        else if(k == 5) add(a, b, 0);
    }

    for(int i = 1; i <= n; i ++)    add(0, i, 1);

    if(spfa())    puts("-1");
    else{
        long long res = 0;
        for(int i = 1; i <= n; i ++)    res += d[i];
        printf("%lld\n", res);
    }

    return 0;
}

区间

S[i] 表示 1 ~ i 中被选出的数的个数 比如 1 ~ 5 中选出了 3 个，s[5] = 3 ，1 ~ 3 中选出了 2 个 ，s[3] = 2。

首先将区间整体向右移动一位，这样能够空出 0 这个位置，方便操作。

1、找出约束条件同时建边
$$ (1) S_i \ge S_{i - 1}\\\ (2) S_i - S_{i - 1} \leq 1 => S_{i - 1} \ge S_i - 1 \\\ (3) S_b - S_{a - 1} \ge c => S_b \ge S_{a - 1} + c $$
2、找到超级源点，以 0 为超级源点，建立一条 0 -> 1 -> 2 -> 3 -> … -> 50001 的路径，每条边的边权是 0。

3、建完图之后，跑一遍最长路（因为是大于关系)

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>

using namespace std;

const int N = 5e4 + 10, M = N * 3;

int h[N], ne[M], e[M], w[M], idx;
int d[N], q[N], n = 50001, m;
bool st[N];

void add(int a, int b, int c)
{
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++;
}

void spfa()
{
    int tt = 1;
    memset(d, -0x3f, sizeof d);
    d[0] = 0;
    st[0] = 1;
    q[0] = 0;

    while(tt != 0){
        int t = q[ -- tt];
        st[t] = 0;

        for(int i = h[t]; ~i; i = ne[i]){
            int v = e[i];
            if(d[v] < d[t] + w[i]){
                d[v] = d[t] + w[i];
                if(!st[v]){
                    st[v] = 1;
                    q[tt ++] = v;
                }
            }
        }
    }
}

int main()
{
    cin >> m;
    memset(h, -1, sizeof h);
    for(int i = 1; i <= n; i ++){
        add(i - 1, i, 0);
        add(i, i - 1, -1);
    }
    for(int i = 1; i <= m; i ++){
        int a, b, c;
        scanf("%d %d %d", &a, &b, &c);
        a ++, b ++ ;
        add(a - 1, b, c);
    }

    spfa();

    printf("%d\n", d[50001]);

    return 0;
}

排队布局

1、找到约束条件，然后建边
$$ \left\\{ \begin{array} \\\ x_i \le x_{i + 1} + 0 \\\ x_b - x_a \le L => x_b \le x_a + L \\\ x_b - x_a \ge D => x_a \le x_b - D \\\ \end{array} \right. $$
2、超级源点，将每个点都压进栈中。

3、以 1 号点为起点跑一遍最短路，因为是小于关系。

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>

using namespace std;

const int N = 1010, M = 21010, inf = 0x3f3f3f3f;

int h[N], ne[M], e[M], w[M], idx;
int d[N], cnt[N], n, m1, m2, q[N];
bool st[N];

void add(int a, int b, int c)
{
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++;
}

bool spfa(int size)
{
    memset(d, 0x3f, sizeof d);
    memset(cnt, 0, sizeof cnt);
    memset(st, 0, sizeof st);
    int tt = 0;
    for(int i = 1; i <= size; i ++){ //等价于建立超级源点，确保可遍历到所有点（所有边）
        q[tt ++] = i;
        st[i] = 1;
        d[i] = 0;
    }

    while(tt != 0){
        int t = q[ -- tt];
        st[t] = 0;

        for(int i = h[t]; ~i; i = ne[i]){
            int v = e[i];
            if(d[v] > d[t] + w[i]){
                d[v] = d[t] + w[i];
                cnt[v] = cnt[t] + 1;
                if(cnt[v] >= n) return true;
                if(!st[v])  st[v] = 1, q[tt ++] = v;
            }
        }
    }
    return false;
}

int main()
{
    cin >> n >> m1 >> m2;
    memset(h, -1, sizeof h);
    for(int i = 1; i < n; i ++) add(i + 1, i, 0);
    for(int i = 1; i <= m1; i ++){
        int a, b, c;
        scanf("%d %d %d", &a, &b, &c);
        add(a, b, c);
    }
    for(int i = 1; i <= m2; i ++){
        int a, b, c;
        scanf("%d %d %d", &a, &b, &c);
        add(b, a, -c);
    }

    if(spfa(n)) puts("-1");
    else{
        spfa(1);
        if(d[n] == inf) puts("-2");
        else    printf("%d\n", d[n]);
    }

    return 0;
}

ZOJ - 2770

1、找到约束条件，建立边
$$ S_i - S_{i - 1} \ge 0 => S_{i - 1} \le S_i\\\ S_i - S_{i - 1} \le C_i => S_i \le S_{i - 1} + C_i \\\ S_b - S_{a - 1} \ge K_i => S_{a - 1} \le S_b - K_i $$
注意这里的起点是 b （也就是 n ）同时求的是 $-K_i$ 的最小值。

2、超级源点 n 能遍历所有点

3、跑一遍最短路 （小于关系）

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>

using namespace std;

const int N = 1010, M = 102010;

int h[N], ne[M], e[M], w[M], idx;
int d[N], cnt[N], n, m, q[N];
bool st[N];

void add(int a, int b, int c)
{
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++;
}

bool spfa()
{
    memset(cnt, 0, sizeof cnt);
    memset(st, 0, sizeof st);
    memset(d, 0x3f, sizeof d);
    int tt = 1;
    q[0] = n;
    st[n] = 1;
    d[n] = 0;

    while(tt != 0){
        int t = q[ -- tt];
        st[t] = 0;

        for(int i = h[t]; ~i; i = ne[i]){
            int v = e[i];
            if(d[v] > d[t] + w[i]){
                d[v] = d[t] + w[i];
                cnt[v] = cnt[t] + 1;
                if(cnt[v] >= n + 1) return true;
                if(!st[v])  st[v] = 1, q[tt ++] = v;
            }
        }
    }

    return false;
}

int main()
{
    while(cin >> n >> m){
        memset(h, -1, sizeof h);
        idx = 0;
        for(int i = 1; i <= n; i ++){
            int x;
            scanf("%d", &x);
            add(i - 1, i, x);
            add(i, i - 1, 0);
        }
        for(int i = 1; i <= m; i ++){
            int a, b, c;
            scanf("%d %d %d", &a, &b, &c);
            add(b, a - 1, -c);
        }
        // spfa();
        // for(int i = 1; i <= n; i ++)
        //     printf("%d\n", d[i]);

        if(!spfa()) printf("%d\n", -d[0]);
        else
            puts("Bad Estimations");
    }
    return 0;
}

HDU - 1534

题意：有n个任务，给出完成n个任务所需时间，以及一些任务安排。任务安排有四种：

FAS a b：任务a需在任务b开始后完成。

FAF a b：任务a需在任务b完成后完成。

SAF a b：任务a需在任务b完成后开始。

SAS a b：任务a需在任务b开始后开始。

1、找到约束条件，建立边

FAS a b：d[a]+x[a]>=d[b] => d[a] >= d[b] + x[a]

FAF a b：d[a]+x[a]>=d[b]+x[b] => d[a] >= d[b] + x[b] - x[a]

SAF a b：d[a]>=d[b]+x[b]

SAS a b：d[a]>=d[b]

2、超级源点 0，d[i] - d[0] >= 0，代表每个任务都可以在时刻 0 开始。

3、从 0 开始跑一遍最长路。

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>

using namespace std;

const int N = 1010, M = 1e5 + 10;

int h[N], ne[M], e[M], w[M], idx;
int n, m, x[N], d[N], cnt[N], q[N];
bool st[N];

void add(int a, int b, int c)
{
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++;
}

bool spfa()
{
    memset(cnt, 0, sizeof cnt);
    memset(st, 0, sizeof st);
    memset(d, -0x3f, sizeof d);
    d[0] = 0;
    st[0] = 1;
    int tt = 1;
    q[0] = 0;

    while(tt != 0){
        int t = q[ -- tt];
        st[t] = 0;

        for(int i = h[t]; ~i; i = ne[i]){
            int v = e[i];
            if(d[v] < d[t] + w[i]){
                d[v] = d[t] + w[i];
                cnt[v] = cnt[t] + 1;
                if(cnt[v] >= n + 1) return true;
                if(!st[v])  st[v] = 1, q[tt ++] = v;
            }
        }
    }
    return false;
}

int main()
{
    int cas = 1;
    while(cin >> n, n){
        memset(h, -1, sizeof h);
        idx = 0;
        for(int i = 1; i <= n; i ++)    scanf("%d", &x[i]);
        char str[5];
        while(scanf("%s", str) && str[0] != '#'){
            int a, b;
            cin >> a >> b;
            if(str[0] == 'F' && str[2] == 'S')  add(b, a, -x[a]);
            else if(str[0] == 'F' && str[2] == 'F')
                add(b, a, x[b] - x[a]);
            else if(str[0] == 'S' && str[2] == 'F')
                add(b, a, x[b]);
            else if(str[0] == 'S' && str[2] == 'S')
                add(b, a, 0);
        }

        for(int i = 1; i <= n; i ++)    add(0, i, 0);
        printf("Case %d:\n", cas ++);
        if(!spfa()){
            for(int i = 1; i <= n; i ++)
                printf("%d %d\n", i, d[i]);
        }else{
            puts("impossible");
        }
        cout << endl;
    }
    return 0;
}

HDU - 3666

1、找到约束条件。
$$ L \le x[i][j] * a[i] / b[j] \le R \\\=> L / x[i][j] \le a[i] / b[j] \le R / x[i][j] \\\=> L / x[i][j] \le a[i] / b[j] \\\ a[i]/b[j] \le R / x[i][j] \\\ $$
通过连边取对数就可以得到
$$ log(b[j]) - log(a[i]) \le -log(L / x[i][j]) \\\log(a[j]) - log(b[i]) \le log(R / x[i][j]) $$

add(i, j + n, -log(L / x[i][j])), add(j + n, i, log(R / x[i][j]))

2、超级源点 0，因为每个点都必须大于 0。

3、以源点 0 跑一遍最短路。

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
#include<queue>

using namespace std;

const int N = 1010, M = N * N * 2;
const double inf = 1e9;

int h[N], ne[M], e[M], idx;
double d[N], w[M];
int cnt[N], n, m, l, r, q[N];
bool st[N];

void add(int a, int b, double c)
{
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++;
}

bool spfa()
{
    for(int i = 1; i <= n + m + 1; i ++)    d[i] = inf;
    memset(st, 0, sizeof st);
    memset(cnt, 0, sizeof cnt);
    int tt = 1;
    q[0] = 0;
    d[0] = 0.0;
    cnt[0] = 1;
    st[0] = 1;
    while(tt != 0){
        int t = q[ -- tt];
        st[t] = 0;

        if(cnt[t] > n + m)  return true;
        for(int i = h[t]; ~i; i = ne[i]){
            int v = e[i];
            double z = w[i];
            if(d[v] > d[t] + z){
                d[v] = d[t] + z;
                if(!st[v]){
                    st[v] = 1;
                    cnt[v] ++;
                    q[tt ++] = v;
                }
            }
        }
    }
    return false;
}

int main()
{
    while(cin >> n >> m >> l >> r){
        memset(h, -1, sizeof h);
        idx = 0;

        for(int i = 1; i <= n + m; i ++)    add(0, i, 0.0);
        for(int i = 1; i <= n; i ++)
            for(int j = 1; j <= m; j ++){
                int a;
                scanf("%d", &a);
                add(i, j + n, log(1.0 * a / l));
                add(j + n, i, log(1.0 * r / a));
            }

        if(!spfa()) puts("YES");
        else    puts("NO");
    }

    return 0;
}

HDU - 3440

1、找到约束条件。d[i] 表示下标为 i 的房子距离最左边的大小
$$ d[i + 1] - d[i] \ge 1 \\\将房子的高度按从小到大排序之后 d[j + 1] - d[j] \le D $$
因为题目规定房子之间的相对位置不能换同时我们也规定了 d[i] 表示房子距离最左边的大小，所以将房子按照高度大小排序之后，必须下标小的连向下标大的

2、以最高的房子和最低的房子的下标最小值为起点开始跑一遍最短路。

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>

using namespace std;

const int N = 1010, M = N * 3, inf = 0x3f3f3f3f;

int h[N], ne[M], e[M], w[M], idx;
int d[N], cnt[N], n, D, q[N], T;
struct node{
    int x, id;
    bool operator < (node t) const{
        return x < t.x;
    }
}g[N];
bool st[N];

void add(int a, int b, int c)
{
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++;
}

bool spfa(int s)
{
    memset(d, 0x3f, sizeof d);
    memset(st, 0, sizeof st);
    memset(cnt, 0, sizeof cnt);
    d[s] = 0;
    int tt = 1;
    q[0] = s;
    cnt[s] = 1;
    while(tt != 0){
        int t = q[ -- tt];
        st[t] = 0;

        for(int i = h[t]; ~i; i = ne[i]){
            int v = e[i];
            if(d[v] > d[t] + w[i]){
                d[v] = d[t] + w[i];
                if(!st[v]){
                    st[v] = 1;
                    q[tt ++] = v;
                    if( ++ cnt[v] > n)  return false;
                }
            }
        }
    }
    return true;
}

int main()
{
    cin >> T;
    int cas = 1;
    while(T --){
        memset(h, -1, sizeof h);
        idx = 0;
        cin >> n >> D;
        for(int i = 1; i <= n; i ++){
            scanf("%d", &g[i].x);
            g[i].id = i;
        }
        sort(g + 1, g + 1 + n);
        for(int i = 1; i < n; i ++) add(i + 1, i, -1);
        sort(g + 1, g + 1 + n);
        for(int i = 1; i < n; i ++){
            add(min(g[i].id, g[i + 1].id), max(g[i].id, g[i + 1].id), D);
        }

        int s = min(g[1].id, g[n].id), e = max(g[1].id, g[n].id);
        printf("Case %d: ", cas ++);
         if (spfa(s))
            printf("%d\n", d[e]);
        else
            puts("-1");

    }
    return 0;
}

POJ - 1716

1、找到约束条件

S[i] 表示区间 [1, i] 中有多少个元素
$$ 0 \le S_{i} - S_{i - 1} \le 1 \\\ => S_{i} \ge S_{i - 1} \\\ S_{i - 1} \ge S_{i} + 1 \\\S_b - S_{a - 1} \ge 2 => S_{b} \le S_{a - 1} + 2 $$
2、超级源点 0 3、跑最长路

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<queue>

using namespace std;

const int N = 10010, M = N * 3;

int h[N], ne[M], e[M], w[M], idx;
int d[N], n = 10001, m, q[N];
bool st[N];

void add(int a, int b, int c)
{
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++;
}

void spfa()
{
    memset(d, -0x3f, sizeof d);
    memset(st, 0, sizeof st);
    queue < int > q;
    q.push(0);
    st[0] = 1;
    d[0] = 0;
    while(q.size()){
        int t = q.front();q.pop();
        st[t] = 0;

        for(int i = h[t]; ~i; i = ne[i]){
            int v = e[i];
            if(d[v] < d[t] + w[i]){
                d[v] = d[t] + w[i];
                if(!st[v])  st[v] = 1, q.push(v);
            }
        }
    }
}

int main()
{
    while(cin >> m){
        memset(h, -1, sizeof h);
        idx = 0;
        int mx = -1;
        for(int i = 1; i <= m; i ++){
            int a, b;
            scanf("%d %d", &a, &b);
            a ++, b ++;
            add(a - 1, b, 2);
            mx = max(mx, b);
        }
        for(int i = 1; i <= mx; i ++){
            add(i, i - 1, -1), add(i - 1, i, 0);
        }
        spfa();
        printf("%d\n", d[mx]);
    }
    return 0;
}

POJ - 2983

1、找到约束条件 设 d[i] 为 0 号站离 i 号防御站的距离，
$$ 操作P : d[a] - d[b] = C \\\=> d[a] \le d[b] + C \\\ d[b] \le d[a] - C \\\操作V : d[a] - d[b] \ge 1 \\\=> d[b] \le d[a] - 1 $$
2、超级源点 0 ，向每个点建边

3、求最短路

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<queue>

using namespace std;

const int N = 1010, M = 2e5 + N;

int h[N], ne[M], e[M], w[M], idx;
int d[N], cnt[N], n, m, q[N];
bool st[N];

void add(int a, int b, int c)
{
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++;
}

bool spfa()
{
    memset(cnt, 0, sizeof cnt);
    memset(st, 0, sizeof st);
    memset(d, 0x3f, sizeof d);
    int tt = 0;
    for(int i = 1; i <= n; i ++){
        q[tt ++] = i;
        st[i] = 1;
    }

    while(tt != 0){
        int t = q[ -- tt];
        st[t] = 0;

        for(int i = h[t]; ~i; i = ne[i]){
            int v = e[i];
            if(d[v] > d[t] + w[i]){
                d[v] = d[t] + w[i];
                if(!st[v]){
                    st[v] = 1;
                    q[tt ++] = v;
                    if(++ cnt[v] > n)   return true;
                }
            }
        }
    }

    return false;
}

int main()
{
    while(cin >> n >> m){
        memset(h, -1, sizeof h);
        idx = 0;
        for(int i = 1; i <= m; i ++){
            char op;
            cin >> op;
            if(op == 'P'){
                int a, b, c;
                scanf("%d %d %d", &a, &b, &c);
                add(b, a, c), add(a, b, -c);
            }else{
                int a, b;
                scanf("%d %d", &a, &b);
                add(a, b, -1);
            }
        }

        if(spfa())
            printf("Unreliable\n");
        else
            printf("Reliable\n");
    }
    return 0;
}