时间复杂度由$O(NM)$降为了$O(n)$

匹配演示

前缀与后缀

"前缀"指除了最后一个字符以外，一个字符串的全部头部组合；
"后缀"指除了第一个字符以外，一个字符串的全部尾部组合。
eg. "ABCD"的前缀为[A, AB, ABC]，后缀为[BCD, CD, D]

KMP代码详细注解

1.next数组

/*
1.ne数组(两个指针在子串上移动)：
-> 对于子串来说的，预处理子串的每一个点
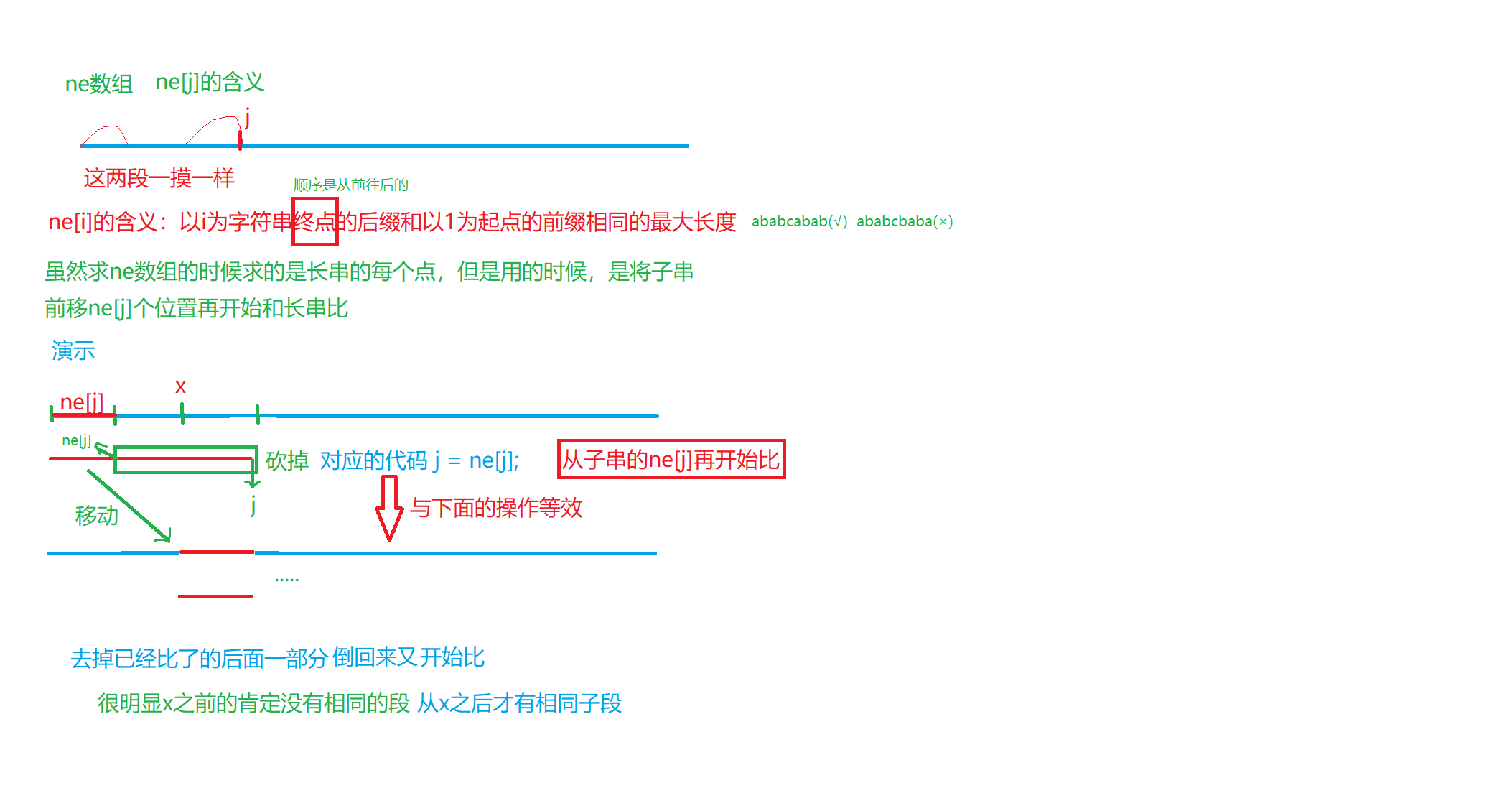
-> ne[i]的含义：以i为字符串终点的后缀和以1为起点的前缀相同的**最大长度**对应的前缀下标.
2.s[]是长串，p[]是子串, n是s的长度，m是p的长度
3. **当我们不成功时, p的最大后缀是和最大前缀一样的, 最大后缀有等于长串后面一段, 所以可以直接从最大前缀的尾节点, 重新继续匹配**
*/

// 为何i从2开始? 后缀从2开始才有后缀
/*
i:子串下标；**j:最大前后缀长度其实也就等价于前缀尾节点编号, 这也是为什么**KMP编号从1开始**, 如果从0开始, 
长度与编号就不对应了**  
*/
for (int i = 2, j = 0; i <= m; i ++ )
{
    // 递推解决 不行就上一个的长度 不需要长度减一减一的看，因为相同的段只有前面已经相同了的段才可能加上一个新的相同
    while (j && p[i] != p[j + 1]) j = ne[j];
    // 上一个的长度加上现在新增的一个点即为该新增点的最大长度
    if (p[i] == p[j + 1]) j ++ ; // p[j + 1]就是前缀的最后一个数，p[i]就是后缀的最后一个数
    ne[i] = j;  // 赋值该点的最大长度
}

2.匹配

// 匹配 -> 见图解代码模拟
for (int i = 1, j = 0; i <= n; i ++ )  // j为p串的指针，i为s串的指针
{
    while (j && s[i] != p[j + 1]) j = ne[j];
    if (s[i] == p[j + 1]) j ++ ;
    if (j == m)
    {
        j = ne[j];
        // 匹配成功后的逻辑
    }
}

应用

查找字符串中某一子串出现的次数

另附暴力做法

for (int i = 1; i <= n; i ++ )
{
    bool flag = true;
    for (int j = 1; j <= m; j ++ )
    {
        if (s[i + j - 1] != p[j])
        {
            flag=false;
            break;
        }
    }
}

例题 安徽19省赛括号序列