1.数独

这道题我感觉还是挺麻烦的。dfs的话做的较少，这个题剪枝比较多。
首先的话大致看一下搜索顺序：①随意选取一个格子 ② 在这个格子放入一个符合规则的数字 ③ dfs下一层，去填下一个格子
要想剪枝的话，第一步应该选择情况较少的格子，所以大致思路就是 用col[i] row[j] num[i/3][j/3] 分别记录一下每列、每行、每个小格子中可以用哪些数字（用二进制表示，1->可用 0->不可用） 然后用col&row&num 的话就可以找到某具体的一个小格子 ，哪些数可以填 哪些数不可以填，用lowbit操作可以返回最后一位1，这样的话就能把具体哪位1得出来，即哪个数字可以用。然后就把数字填上去，记得改变各个状态数组，col row num。还要记得恢复现场
然后给一下代玛

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstdlib>

using namespace std;
const int N = 9;
char str[100];
int row[N],col[N],num[3][3];//二进制存 当前行可用哪个数字
int ones[1<<N],cnt,map[1<<N];//ones 表示 第i个数 有几个1  用于求哪一个格子所选方案最少 
                            // map 用于映射  第i个数 二进制  表示第几位是1  如100->3 
inline int lowbit(int x)
{
    return x&-x;
}
inline  int get(int i,int j)
{
    return row[i]&col[j]&num[i/3][j/3];//返回 某一数独格 到底能放那几个数的二进制表示形式 
}
void init()//init函数的作用在用把row col num 数组每个状态都变成全1的状态， 即每一个二进制位都是可以取的。 
{
    for(int i=0;i<N;i++)
    {
        row[i]=(1<<N)-1;
        col[i]=(1<<N)-1;
    }
    for(int i=0;i<3;i++)
    for(int j=0;j<3;j++)
    num[i][j]=(1<<N)-1;
}
bool dfs(int cnt)
{
    if (!cnt) return true;

    // 找出可选方案数最少的空格
    int minv = 10;
    int x, y;
    for (int i = 0; i < N; i ++ )
        for (int j = 0; j < N; j ++ )
            if (str[i * 9 + j] == '.')
            {
                int t = ones[get(i, j)];
                if (t < minv)
                {
                    minv = t;
                    x = i, y = j;
                }
            }




    //找出 可选方案书最少的格子后 开始 模拟填数独
    for(int i=get(x,y);i;i-=lowbit(i))
    {
        //i返回最后一位1 然后要把这个i映射成  第几位
        int t= map[lowbit(i)];
        row[x]-=1<<t;// 第id置为0 说明数字已经用了
        col[y]-=1<<t; 
        num[x/3][y/3]-=1<<t;
        str[x*9+y]='1'+t;//加一是因为 t从0~8 要重新映射成1~9 
        if(dfs(cnt-1)) return true;
        row[x]+=1<<t;
        col[y]+=1<<t;
        num[x/3][y/3]+=1<<t;
        str[x*9+y]='.';
    }
    return false;
}
int main()
{

    for(int i=0;i<N;i++)
    {
        map[1<<i]=i;// 把 100 映射成3   即 Lowbit(x)取出最后一位1的时候 直接转换成 第几个位置的数字是可以用的; 
    }
    for(int i=0;i<1<<N;i++)
    {
        int s=0;
        for(int j=i;j;j-=lowbit(j)) s++;
        ones[i]=s;//统计i的二进制有多少个1 
    }
    while(cin>>str,str[0]!='e')
    {   init();
        int cnt=0;
        for(int i=0,k=0;i<N;i++)
        {
            for(int j=0;j<N;j++,k++)
            {
                if(str[k]!='.')
                {
                    int t=str[k]-'1';//把1~9 映射成0~8
                    row[i]-=1<<t;//i行  t位 不能取  置为0
                    col[j]-=1<<t;//j列 同理
                    num[i/3][j/3]-=1<<t;

                }
                else cnt++; 
            }
        }

    dfs(cnt);
    cout<<str<<endl;
    }

    return 0;
} 

2. 排书

emm 按道理来说的话， DFS是不能求这种最优解问题的， 不过DFS+迭代加深是可以解决这种问题的（自己这么理解） 所以可以用IDA 来做， 另外IDA也算是一种剪枝 。
IDA 算法比较重要的就是估价函数，估价函数一般用来表示解决这个问题需要的最少次数是多少，然后设置depth不断向下递归。例如本题 5次或以上就可以return 了，很适合用IDA算法。
求估价函数过程如下：

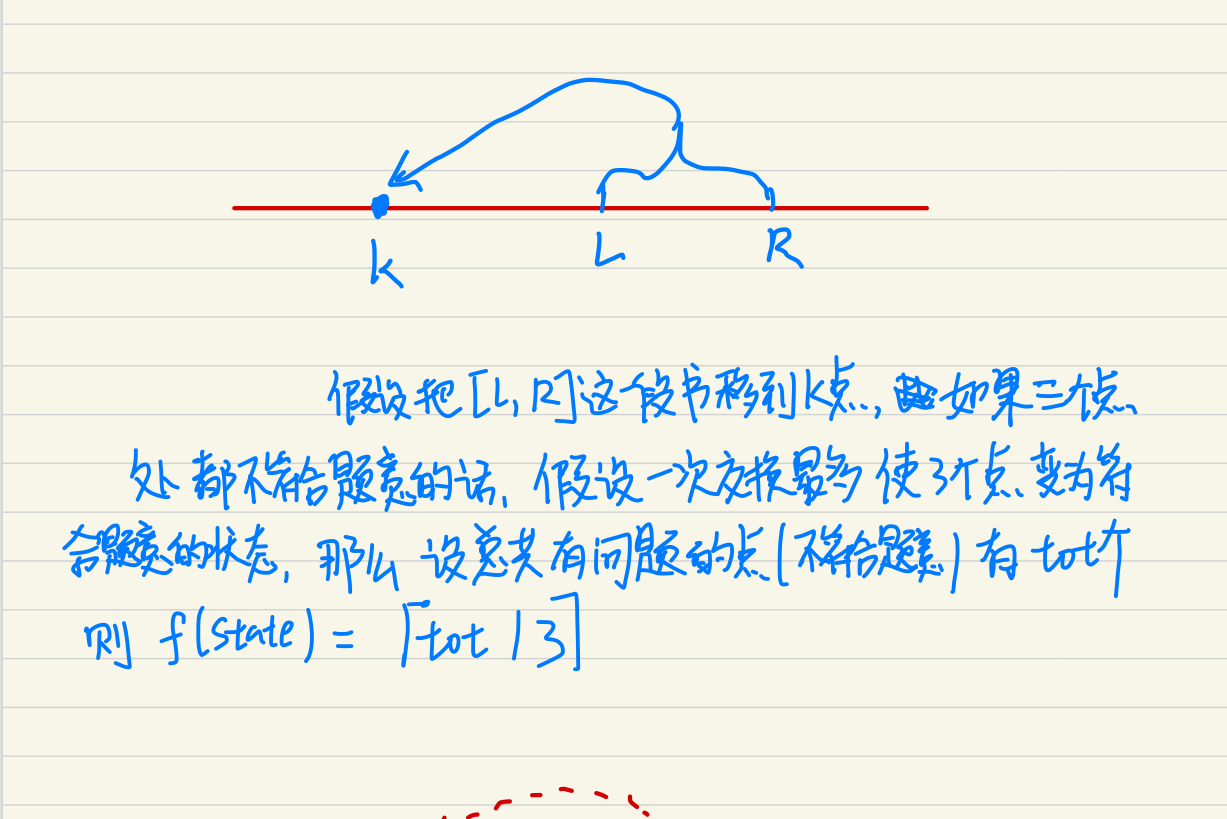
然后贴一下代玛：(上取整用ceil只能过百分之90 真的蛋疼)

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<cmath>
using namespace std;
const int N=16;
int T,n;
int num[N];
int w[6][N];//用于拷贝数组  方便交换书这个过程的实现 
bool check()
{
    for(int i=0;i<n;i++)
    {
        if(num[i]!=i+1) return false;
    }
    return true;
}
int f()
{
    // 求估值函数  先求不符合题意的点的个数
    int tot=0;
    for(int i=1;i<n-1;i++)
    {
        if(num[i+1]!=num[i]+1) tot++;
     }
     return (tot+2)/3;
     //return ceil(tot/3); 
}
bool dfs(int depth , int maxdepth)
{
    if(depth+f()>maxdepth) return false;//当前深度加f都大于等于标准的话  铁return 
    if(check()) return true;//开局检查一下
    // 接下来就开始模拟换书过程开始向下递归了
     for(int len=0;len<n;len++)
     {
        for(int l=0;l+len-1<n;l++)
        {
            int r=l+len-1;
            //枚举出 左右端点 ，然后枚举要把这排书插到哪
             for(int k=r+1;k<n;k++)
             {
                memcpy(w[depth],num,sizeof(num));
                int x,y;
                for( x=r+1,y=l;x<=k;x++,y++) num[y]=w[depth][x]; 
                for(x=l;x<=r;x++,y++) num[y]=w[depth][x];
                if(dfs(depth+1,maxdepth)) return true;//下一层搜索
                 memcpy(num,w[depth],sizeof(num)); 
            } 
         }
     }

    return false;
}
int main()
{
    cin>>T;
    while(T--)
    {
        cin>>n;
        for(int i=0;i<n;i++)
        scanf("%d",&num[i]);
        int depth=0;//设置深度 ida*标准套路
        while(depth<5&&!dfs(0,depth)) depth++;
        if(depth>=5) cout<<"5 or more"<<endl;
        else cout<<depth<<endl;
    }
    return 0;
}