最近公共祖先
给定一棵有根树,若节点 z 既是节点 x 的祖先,也是节点 y 的祖先,则称 z 是 x,y 的公共祖先(祖先是指当前节点到树根节点的路径上的所有节点都是当前节点的所有祖先)。
在 x,y 的所有公共祖先中,深度最大的一个称为 x,y 的最近公共祖先
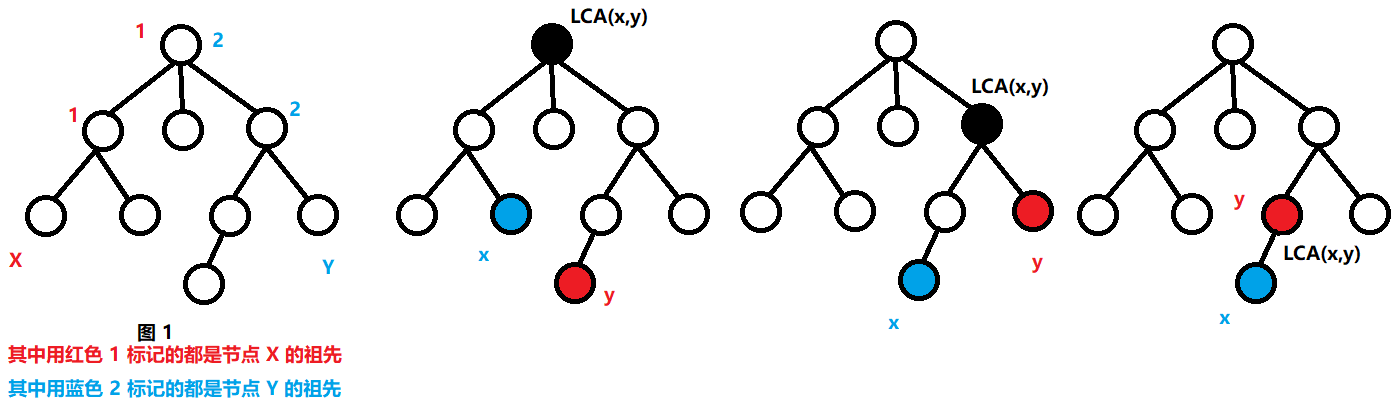
LCA(x, y) 是 x 到跟的路径与 y 到跟的路径的交点。它也是 x 与 y 之间的路径上深度最小的节点。
树上倍增法
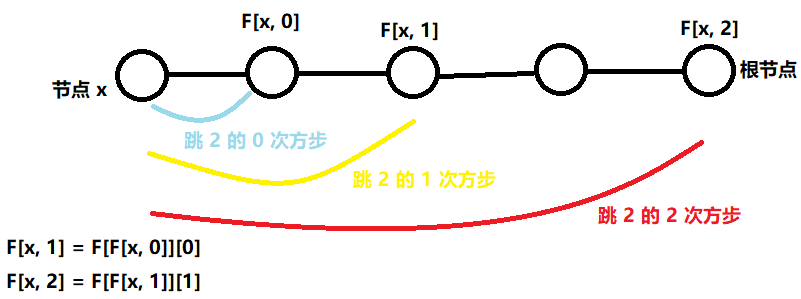
设 F[x, k] 表示 x 的 第 $2_k$ 个祖先,即 x 节点向根节点走 $2_k$ 步到达的节点。f[x, 0] 就是 x 节点第一个祖先(也即父节点)。若该节点不存在(跳到了根节点外),我们则令 f[x, k] = 0
$$
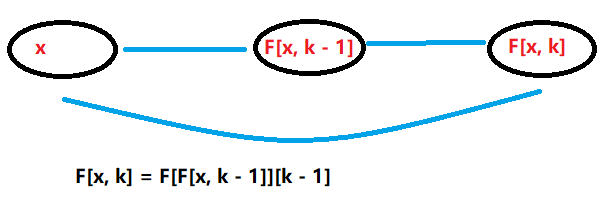
\forall k \in [1, logn], F[x, k] = F[F[x, k - 1]][k - 1]
$$
首先要先预处理出 树的每个节点的 F 数组和 深度数组 dep。通过 BFS 按照层次顺序,在节点入队之前,计算每个节点的 F 数组和 深度数组 dep。
void bfs(int root)
{
memset(dep, 0x3f, sizeof dep);
dep[0] = 0, dep[root] = 1;
queue < int > q;
q.push(root);
while(q.size()){
int t = q.front();q.pop();
for(int i = h[t]; ~i; i = ne[i]){
int v = e[i];
if(dep[v] > dep[t] + 1){
dep[v] = dep[t] + 1;
f[v][0] = t;
for(int i = 1; i <= 16; i ++){
f[v][i] = f[f[v][i - 1]][i - 1];
}
q.push(v);
}
}
}
}
基于 F 数组计算 LCA(x, y)
1、设 d[x] 表示 x 的深度,假设 $d[x] \ge d[y]$。
2、用二进制拆分思想,把 x 向上调整到与 y 同一深度。
具体来说,就是依次尝试从 x 向上走 k = $2^{logn}, … , 2^1, 2^0$ 步,检查到达的节点是否大于等于 y 节点,在每次检查中,若是,则令 x = F[x, k]。
3、若此时 x == y ,说明已经找到了最近公共祖先
4、用二进制拆分思想,把 x,y 同时向上调整,并保持深度一致且二者不会相会。
5、此时 x, y 必定只差一步就相会了,它们的父节点 F[x, 0] 就是最近公共祖先。
int lca(int a, int b)
{
if(dep[a] < dep[b]) swap(a, b);
for(int i = 16; i >= 0; i -- ){
if(dep[f[a][i]] >= dep[b]) a = f[a][i];
}
if(a == b) return a;
for(int i = 16; i >= 0; i --){
if(f[a][i] != f[b][i]){
a = f[a][i];
b = f[b][i];
}
}
return f[a][0];
}
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<queue>
using namespace std;
const int N = 4e4 + 10, M = N * 2;
int h[N], e[M], ne[M], idx;
int f[N][20], dep[N], n, m;
void add(int a, int b)
{
e[idx] = b, ne[idx] = h[a], h[a] = idx ++;
}
void bfs(int root)
{
memset(dep, 0x3f, sizeof dep);
dep[0] = 0, dep[root] = 1;
queue < int > q;
q.push(root);
while(q.size()){
int t = q.front();q.pop();
for(int i = h[t]; ~i; i = ne[i]){
int v = e[i];
if(dep[v] > dep[t] + 1){
dep[v] = dep[t] + 1;
f[v][0] = t;
for(int i = 1; i <= 16; i ++){
f[v][i] = f[f[v][i - 1]][i - 1];
}
q.push(v);
}
}
}
}
int lca(int a, int b)
{
if(dep[a] < dep[b]) swap(a, b);
for(int i = 16; i >= 0; i -- ){
if(dep[f[a][i]] >= dep[b]) a = f[a][i];
}
if(a == b) return a;
for(int i = 16; i >= 0; i --){
if(f[a][i] != f[b][i]){
a = f[a][i];
b = f[b][i];
}
}
return f[a][0];
}
int main()
{
cin >> n;
memset(h, -1, sizeof h);
int root = 0;
for(int i = 1; i <= n; i ++){
int a, b;
scanf("%d %d", &a, &b);
if(b == -1) root = a;
else add(a, b), add(b, a);
}
bfs(root);
cin >> m;
while(m -- ){
int a, b;
scanf("%d %d", &a, &b);
int p = lca(a, b);
if(p == a) puts("1");
else if(p == b) puts("2");
else puts("0");
}
return 0;
}
Tarjan 算法
tarjan 算法本质上是使用并查集对 “向上标记法” 的优化。它是一个离线算法,需要把 m 个询问一次性读入,统一计算,最后统一输出。
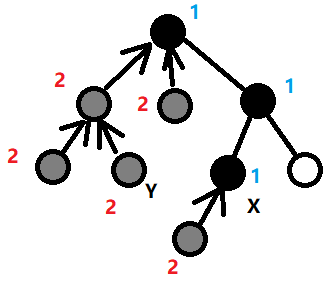
在深度优先遍历的任意时刻,树中节点分为三类:
1、已经访问完毕并且回溯的节点。在这些节点上标记一个整数 2。
2、已经开始递归,但尚未回溯的节点。这些节点就是当前正在访问的节点 x 以及 x 的祖先。在这些节点上标记一个整数 1。
3、尚未访问的节点。这些节点没有标记。
对于正在访问的节点 x,它到根节点的路径已经标记为 1 。若 y 是已经访问完毕并且回溯的节点(被标记了 2),则 LCA(x, y)就是从 y 向上走到根,第一个遇到的标记为 1 的节点。
可以利用并查集进行优化,当一个节点获得整数 2 的标记时,把它所在的集合合并到它的父节点所在的集合中(合并时它的父节点标记一定为 1,且单独构成一个集合)。
这相当于每个完成回溯的节点都有一个指针指向它的父节点,只需查询 y 所在集合的代表元素,就等价于从 y 向上一直走到一个开始递归但尚未回溯的节点(具有标记 1),即 LCA(x, y)。
在 x 回溯之前,标记情况与合并情况如下图所示。黑色表示标记为 1,灰色表示标记为 2。
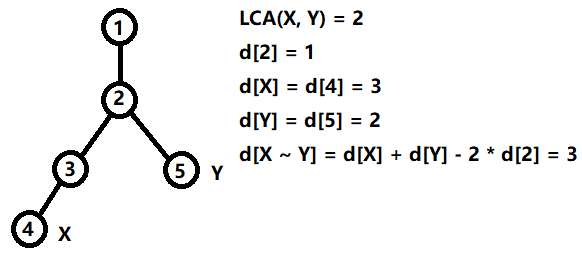
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<queue>
using namespace std;
typedef pair < int , int > pii;
const int N = 2e4 + 10, M = N * 2;
int h[N], e[M], ne[M], w[M], idx;
int d[N], f[N], ans[N], st[N], n, m;
vector< pii > q[N];
void add(int a, int b, int c)
{
e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++;
}
void dfs(int u, int fa)
{
for(int i = h[u]; ~i; i = ne[i]){
int v = e[i];
if(v == fa) continue;
d[v] = d[u] + w[i];
dfs(v, u);
}
}
int find(int x)
{
if(x != f[x]) f[x] = find(f[x]);
return f[x];
}
void tarjan(int u)
{
st[u] = 1;
for(int i = h[u]; ~i; i = ne[i]){
int v = e[i];
if(!st[v]){
tarjan(v);
f[v] = u;
}
}
for(int i = 0; i < q[u].size(); i ++){
pii t = q[u][i];
int a = t.first, id = t.second;
if(st[a] == 2){
int p = find(a);
ans[id] = d[u] + d[a] - 2 * d[p];
}
}
st[u] = 2;
}
int main()
{
cin >> n >> m;
memset(h, -1, sizeof h);
for(int i = 1; i < n; i ++){
int a, b, c;
scanf("%d %d %d", &a, &b, &c);
add(a, b, c), add(b, a, c);
}
for(int i = 1; i <= n; i ++) f[i] = i;
for(int i = 1; i <= m; i ++){
int a, b;
scanf("%d %d", &a, &b);
q[b].push_back({a, i});
q[a].push_back({b, i});
}
dfs(1, -1);
tarjan(1);
for(int i = 1; i <= m; i ++){
printf("%d\n", ans[i]);
}
return 0;
}
假设无向图的严格最小生成树的边权之和为 sum,严格次小生成树就是边权和大于 sum 的生成树中最小的一个。
定理:对于一张无向图,如果存在最小生成树和严格次小生成树,那么对于任何一棵最小生成树,都存在一棵严格次小生成树,使得这两棵树只有一条边不同。
先求出任意一棵最小生成树,设边权之和为 sum。我们称在这棵最小生成树中的 n - 1 条边为 “树边”,其他 m - n + 1 条边为 “非树边”。
我们枚举每一条非树边 (x, y, z) 添加到最小生成树中,会与树上 x, y 之间的路径一起形成一个环。
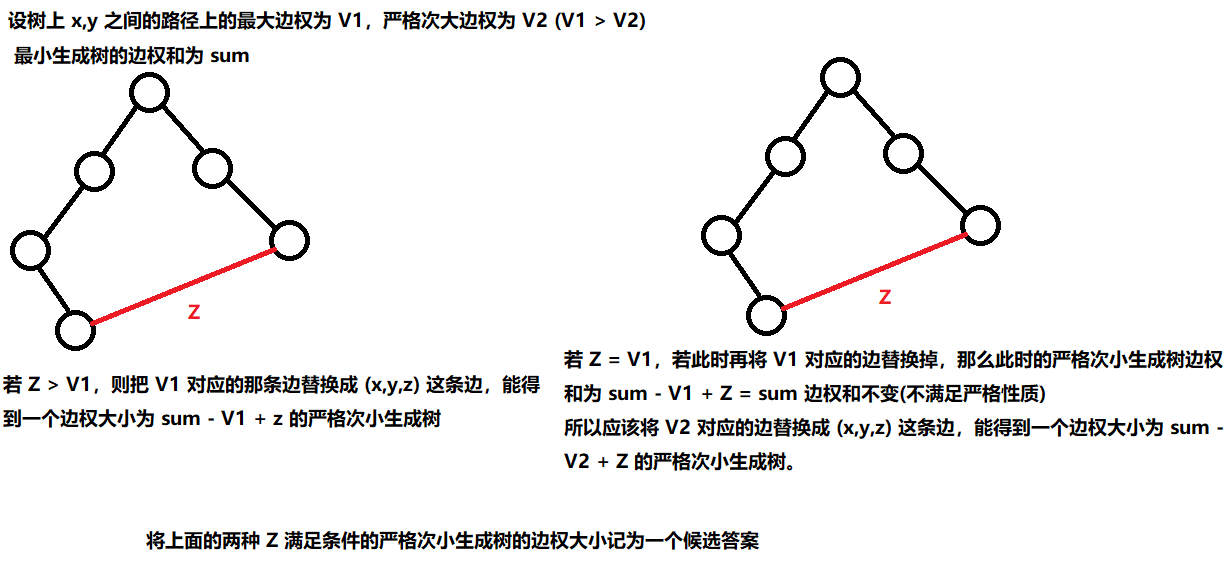
枚举每条非树边,添加到最小生成树中,计算出上述所有”候选答案”。在候选答案中取最小值就得到了整张无向图的严格次小生成树。
如何快速求出一条路径上的最大边权与严格次大边权。可以用树上倍增算法来进行预处理。设 F[x, k] 表示 x 的 $2^k$ 辈祖先,G[x,k,0] 与 G[x, k, 1] 分别表示从 x 到 F[x, k] 的路径上的最大边权和严格次大边权(最大边需要严格大于次大边)。于是 $\forall k \in [1, logn]$ 有:
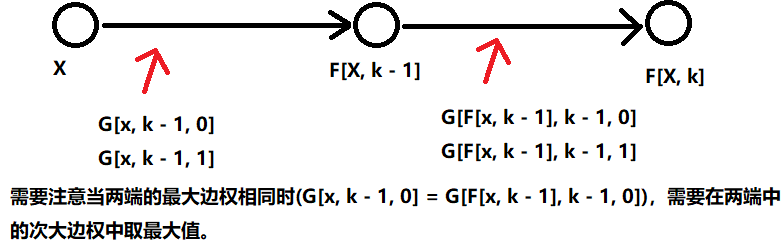
$$
F[x, k] = F[F[x, k - 1], k - 1] \\\
G[x, k, 0] = max(G[x, k - 1, 0], G[F[x, k - 1], k - 1, 0]) \\\
G[x, k, 1] =
\left\\{
\begin{array}{c}
max(G[x, k - 1, 1], G[F[x, k - 1], k - 1, 1]), G[x, k - 1, 0] = G[f[x, k - 1], k - 1, 0] \\\
max(G[x, k - 1, 0], G[F[x, k - 1], k - 1, 1]), G[x, k - 1, 0] < G[F[x, k - 1], k - 1, 0] \\\
max(G[x, k - 1, 1], G[F[x, k - 1], k - 1, 0]), G[x, k - 1, 0] > G[F[x, k - 1], k - 1, 0]
\end{array}
\right.
$$
接下来考虑每条非树边 (x, y, z)。采用倍增计算 LCA(x, y) 的框架,x , y 每向上移动一段路径,就把该路径对应的最大边权、严格次大边权统计出来,最后可以得到 x, y 之间的路径上的最大边权、严格次大边权。
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<queue>
using namespace std;
const int N = 1e5 + 10, M = 3e5 + 10, inf = 0x3f3f3f3f;
int h[N], ne[M], e[M], w[M], idx;
int f[N], n, m;
struct node{
int a, b, w;
bool f;
bool operator < (node t) const{
return w < t.w;
}
}g[M];
int fa[N][20], d1[N][20], d2[N][20], dep[N];
long long sum;
void add(int a, int b, int c)
{
e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++;
}
int find(int x)
{
if(x != f[x]) f[x] = find(f[x]);
return f[x];
}
void kru()
{
sum = 0;
for(int i = 1; i <= n; i ++) f[i] = i;
sort(g + 1, g + 1 + m);
for(int i = 1; i <= m; i ++){
int a = g[i].a, b = g[i].b, w = g[i].w;
int f1 = find(a), f2 = find(b);
if(f1 != f2){
f[f1] = f2;
add(a, b, w), add(b, a, w);
sum += w;
g[i].f = 1;
}
}
}
void bfs()
{
memset(dep, 0x3f, sizeof dep);
dep[0] = 0, dep[1] = 1;
queue < int > q;
q.push(1);
while(q.size()){
int t = q.front();q.pop();
for(int i = h[t]; ~i; i = ne[i]){
int v = e[i];
if(dep[v] > dep[t] + 1){
dep[v] = dep[t] + 1;
fa[v][0] = t;
q.push(v);
d1[v][0] = w[i], d2[v][0] = -inf;
for(int k = 1; k < 20; k ++){
int anc = fa[v][k - 1];
fa[v][k] = fa[anc][k - 1];
int dis[4] = {d1[v][k - 1], d2[v][k - 1], d1[anc][k - 1], d2[anc][k - 1]};
d1[v][k] = d2[v][k] = -inf;
for(int j = 0; j < 4; j ++){
int x = dis[j];
if(x > d1[v][k]) d2[v][k] = d1[v][k], d1[v][k] = x;
else if(x < d1[v][k] && x > d2[v][k]) d2[v][k] = x;
}
}
}
}
}
}
int lca(int a, int b, int w)
{
int res = 0;
if(dep[a] < dep[b]) swap(a, b);
for(int i = 19; i >= 0; i --){
if(dep[fa[a][i]] >= dep[b]){
if(d1[a][i] < w) res = max(res, d1[a][i]);
else res = max(res, d2[a][i]);
a = fa[a][i];
}
}
if(a == b) return res;
for(int i = 19; i >= 0; i --){
if(fa[a][i] != fa[b][i]){
if(d1[a][i] < w) res = max(res, d1[a][i]);
else res = max(res, d2[a][i]);
if(d1[b][i] < w) res = max(res, d1[b][i]);
else res = max(res, d2[b][i]);
a = fa[a][i]; b = fa[b][i];
}
}
if(d1[a][0] < w) res = max(res, d1[a][0]);
else res = max(res, d2[a][0]);
if(d1[b][0] < w) res = max(res, d1[b][0]);
else res = max(res, d2[b][0]);
return res;
}
int main()
{
cin >> n >> m;
memset(h, -1, sizeof h);
for(int i = 1; i <= m; i ++){
scanf("%d %d %d", &g[i].a, &g[i].b, &g[i].w);
}
kru();
bfs();
long long res = 1e18;
for(int i = 1; i <= m; i ++){
if(!g[i].f){
int a = g[i].a, b = g[i].b, w = g[i].w;
res = min(res, sum + w - lca(a, b, w));
}
}
cout << res << endl;
return 0;
}
把一条附加边 (x, y) 添加到主要边构成的树中,会与树上 x, y 之间的路径一起形成一个环。如果第一步选择切断 x, y 之间路径上的某条边,那么第二步就必须切断附加边 (x, y) 才能令 Dark 被斩为不连通的两部分。
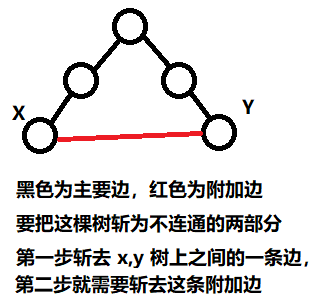
因此,我们称每条附加边 (x, y) 都把树上 x, y 之间的路径上的每条边 “覆盖了一次”。我们只需统计出每条 “主要边” 被覆盖了多少次。若第一步把被覆盖 0 次的主要边切断,则第二步可任意切断一条附加边。若第一步把被覆盖 1 次的主要边切断,则第二步方法唯一。若第一步把被覆盖 2 次及以上的主要边切断,则第二步无论如何操作都没用。
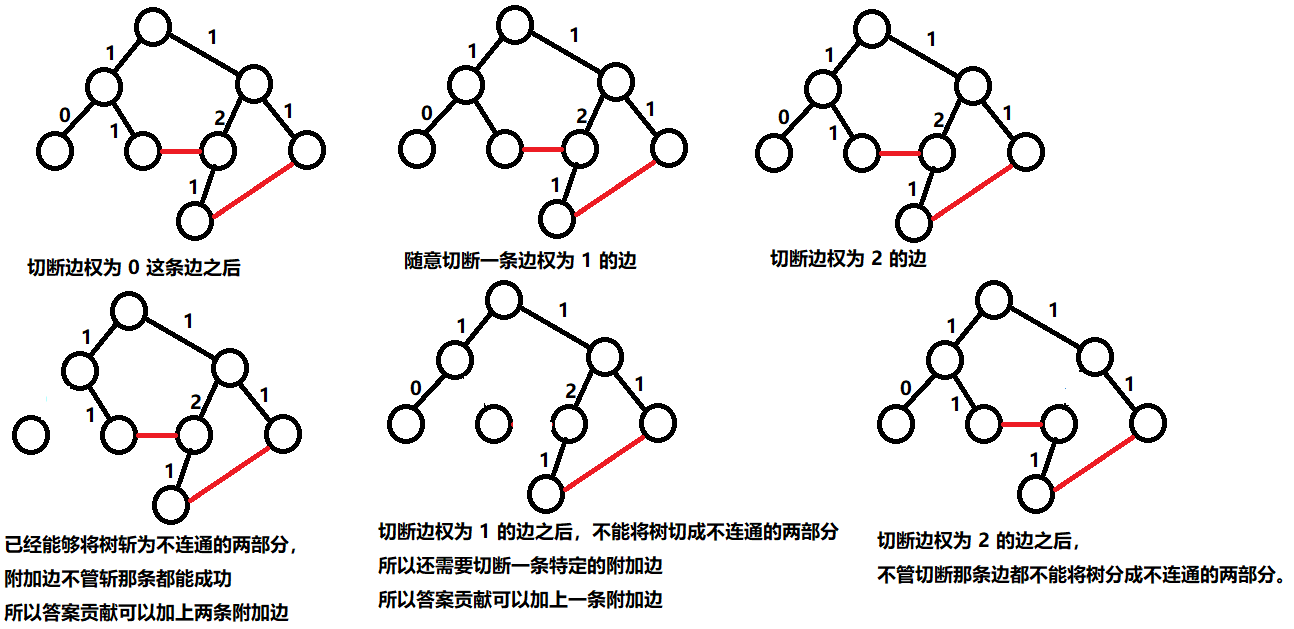
所以问题模型变成:给定一张无向图和一棵生成树,求每条”树边”被”非树边”覆盖了多少次。
我们给树上每个节点一个初始化为 0 的权值,然后对每条非树边(x, y),令节点 x 的权值加 1,节点 y 的权值加 1,节点 LCA(x, y) 的权值减 2。最后对这棵生成树进行一次深度优先遍历,求出 F[x] 表示以 x 为根的子树中各节点的权值之和。F[x] 就是 x 与它的父节点之间的 “树边” 被覆盖的次数。
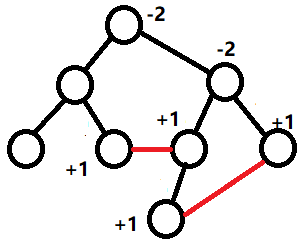
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<queue>
using namespace std;
const int N = 1e5 + 10, M = 3e5 + 10;
int h[N], ne[M], e[M], idx;
int dep[N], f[N], fa[N][20], n, m, ans;
void add(int a, int b)
{
e[idx] = b, ne[idx] = h[a], h[a] = idx ++;
}
void bfs()
{
dep[0] = 0, dep[1] = 1;
queue < int > q;
q.push(1);
while(q.size()){
int t = q.front();q.pop();
for(int i = h[t]; ~i; i = ne[i]){
int v = e[i];
if(!dep[v]){
dep[v] = dep[t] + 1;
fa[v][0] = t;
q.push(v);
for(int k = 1; k < 20; k ++)
fa[v][k] = fa[fa[v][k - 1]][k - 1];
}
}
}
}
int lca(int a, int b)
{
if(dep[a] < dep[b]) swap(a, b);
for(int k = 19; k >= 0; k --){
if(dep[fa[a][k]] >= dep[b])
a = fa[a][k];
}
if(a == b) return a;
for(int k = 19; k >= 0; k --){
if(fa[a][k] != fa[b][k]){
a = fa[a][k];
b = fa[b][k];
}
}
return fa[a][0];
}
int dfs(int u, int fa)
{
int res = f[u];
for(int i = h[u]; ~i; i = ne[i]){
int v = e[i];
if(v == fa) continue;
int s = dfs(v, u);
if(s == 0) ans += m;
else if(s == 1) ans += 1;
res += s;
}
return res;
}
int main()
{
memset(h, -1, sizeof h);
cin >> n >> m;
for(int i = 1; i < n; i ++){
int a, b;
scanf("%d %d", &a, &b);
add(a, b), add(b, a);
}
bfs();
for(int i = 1; i <= m; i ++){
int a, b;
scanf("%d %d", &a, &b);
int p = lca(a, b);
f[a] ++, f[b] ++, f[p] -= 2;
}
dfs(1, -1);
cout << ans << endl;
return 0;
}
本题询问的是森林中任意两点的距离,因为询问的是森林中两点,所以存在两点之间不连通的情况,所以可以用并查集来判断两点之间是否连通,如果两个点之间是连通的,就可以用 d[x] + d[y] - 2 * d[lca(x, y)] 来得到两点之间的距离。
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<queue>
using namespace std;
const int N = 1e4 + 10, M = N * 2, inf = 0x3f3f3f3f;
int h[N], ne[M], e[M], w[M], idx;
int fa[N][20], dep[N], f[N], n, m, c, d[N];
void add(int a, int b, int c)
{
e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++;
}
int find(int x)
{
if(x != f[x]) f[x] = find(f[x]);
return f[x];
}
void bfs(int root)
{
dep[root] = 1;
queue < int > q;
q.push(root);
while(q.size()){
int t = q.front();q.pop();
for(int i = h[t]; ~i; i = ne[i]){
int v = e[i];
if(dep[v] > dep[t] + 1){
dep[v] = dep[t] + 1;
fa[v][0] = t;
d[v] = d[t] + w[i];
q.push(v);
for(int k = 1; k < 20; k ++)
fa[v][k] = fa[fa[v][k - 1]][k - 1];
}
}
}
}
int lca(int a, int b)
{
if(dep[a] < dep[b]) swap(a, b);
for(int k = 19; k >= 0; k --){
if(dep[fa[a][k]] >= dep[b])
a = fa[a][k];
}
if(a == b) return a;
for(int k = 19; k >= 0; k --){
if(fa[a][k] != fa[b][k]){
a = fa[a][k];
b = fa[b][k];
}
}
return fa[a][0];
}
int main()
{
while(cin >> n >> m >> c){
memset(h, -1, sizeof h);
idx = 0;
for(int i = 1; i <= n; i ++) f[i] = i;
for(int i = 1; i <= m; i ++){
int a, b, c;
scanf("%d %d %d", &a, &b, &c);
add(a, b, c), add(b, a, c);
a = find(a), b = find(b);
if(a != b){
f[a] = b;
}
}
memset(dep, 0x3f, sizeof dep);
memset(d, 0, sizeof d);
memset(fa, 0, sizeof fa);
dep[0] = 0;
for(int i = 1; i <= n; i ++){ \\ 因为维护的是森林,所以根节点有很多
if(dep[i] == inf)
bfs(i);
}
for(int i = 1; i <= c; i ++){
int a, b;
scanf("%d %d", &a, &b);
int aa = find(a), bb = find(b);
if(aa == bb){
int p = lca(a, b);
printf("%d\n", d[a] + d[b] - 2 * d[p]);
}else{
puts("Not connected");
}
}
}
return 0;
}
题目求的是一条树链中第 k 大的点权值。
对于每个询问 (x, y) 就暴力的从 x 节点和 y 节点跑到两个点的最近公共祖先,同时记录下路径上经过的所有的点的点权。对记录下的点权数组进行排序就能得到第 k 大的点权。
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<queue>
using namespace std;
const int N = 8e4 + 10, M = N * 2;
int h[N], ne[M], e[M], idx;
int x[N], res[N], cnt, n, k, fa[N], dep[N];
void add(int a, int b)
{
e[idx] = b, ne[idx] = h[a], h[a] = idx ++;
}
void bfs()
{
memset(dep, 0x3f, sizeof dep);
dep[0] = 0, dep[1] = 1;
queue < int > q;
q.push(1);
while(q.size()){
int t = q.front();q.pop();
for(int i = h[t]; ~i; i = ne[i]){
int v = e[i];
if(dep[v] > dep[t] + 1){
dep[v] = dep[t] + 1;
fa[v] = t;
q.push(v);
}
}
}
}
void lca(int a, int b)
{
while(dep[a] > dep[b]){
res[cnt ++] = x[a];
a = fa[a];
}
while(dep[b] > dep[a]){
res[cnt ++] = x[b];
b = fa[b];
}
while(a != b){
res[cnt ++] = x[a];
res[cnt ++] = x[b];
a = fa[a];
b = fa[b];
}
res[cnt ++] = x[a];
}
int main()
{
memset(h, -1, sizeof h);
scanf("%d %d", &n, &k);
for(int i = 1; i <= n; i ++) scanf("%d", &x[i]);
for(int i = 1; i < n; i ++){
int a, b;
scanf("%d %d", &a, &b);
add(a, b), add(b, a);
}
bfs();
while(k --){
int op, a, b;
scanf("%d %d %d", &op, &a, &b);
if(op == 0){
x[a] = b;
continue;
}else{
cnt = 0;
lca(a, b);
if(cnt < op)
puts("invalid request!");
else{
sort(res, res + cnt);
printf("%d\n", res[cnt - op]);
}
}
}
return 0;
}


tql好文要顶