欧拉回路与欧拉路径
如何在图中找到一条覆盖每一条边有且只有一次的通路?
给定一张无向图,若存在一条从节点 S 到节点 T 的路径,恰好不重不漏地经过每条边一次(可以重复经过图中的节点),则称该路径为 S 到 T 的欧拉路。
若存在一条从节点 S 出发的路径,恰好不重不漏地经过每条边一次(可以重复经过图中的节点),最终回到起点 S,则称该路径为欧拉回路。
入度(din):进入该点的边的数量。
出度(dout):走出该点的边的数量。
度(deg):入度 + 出度。
奇结点(奇顶点):连接该结点的边的数量为奇数
偶结点(偶顶点):连接该结点的边的数量为偶数
存在性的判定
对于无向图 G(V, E), $\forall u, v \in V$,如果 u, v 之间存在一个通路,当且仅当任何一个顶点集 V 中的顶点的度 deg(v) 都是偶数时,G 中存在欧拉回路。
对于无向图 G(V, E), $\forall u, v \in V$ ,如果 u, v 之间存在一个通路,当且仅当$\exists v1, v2 \in V (v_1 \neq v_2)$,$v_1$, $v_2$ 的度 deg($v_1$), deg($v_2$) 都为奇数,$\forall v \in (V - \left\{v_1, v_2\right\})$ 的度 deg(v) 都是偶数,G 中存在欧拉路径。这两个度数为奇数的节点就是欧拉路径的起点和终点。
对于有向图 G(V, E), $\forall u, v \in V$, 如果 u, v 之间存在一个通路,当且仅当任何一个顶点集 V 中的顶点的入度等于出度 (din(v) = dout(v)),G 中存在欧拉回路。
对于有向图 G(V, E), $\forall u, v \in V$, 如果 u, v 之间存在一个通路,要么当且仅当任何一个顶点集 V 中的顶点的入度等于出度 (din(v) = dout(v)),要么当且仅当$\exists v1, v2 \in V (v_1 \neq v_2)$,$v_1$ 的入度等于出度加一(din($v_1$) = dout($v_1$) + 1), $v_2$的出度等于入度加一(dout($v_2$) = din($v_2$) + 1),$\forall v \in (V - \left\{v_1, v_2\right\})$ 的顶点的入度等于出度,G中存在欧拉路径。其中 $v_2$ 为起点,$v_1$ 为终点。
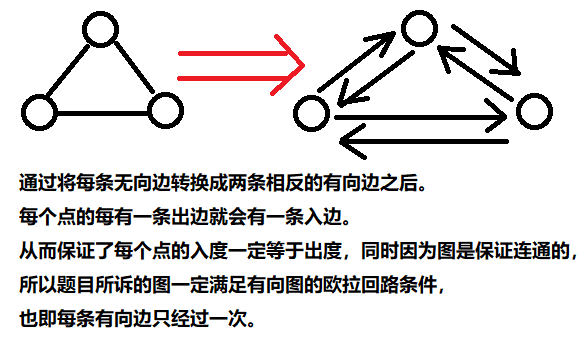
可以将无向图转换为一张有向图
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
using namespace std;
int main()
{
double x1, x2, y1, y2;
cin >> x1 >> x2;
double sum = 0;
while(cin >> x1 >> y1 >> x2 >> y2){
double nx = x1 - x2;
double ny = y1 - y2;
sum += sqrt(nx * nx + ny * ny) * 2;
}
int min = round(sum / 1000 / 20 * 60);
int hours = min / 60;
min %= 60;
printf("%d:%02d\n", hours, min);
return 0;
}
采用邻接表存储无向图,我们可以在访问一条边 (x, y) 后,及时修改表头 h[x],令它指向下一条边。这样我们每次只需取出 h[x] ,就自然跳过了所有已经访问过的边。
链式前向星建边的时候
对于无向图其在读入的时候的边为 x , 链式前向星中的边的编号为 (x - 1) * 2 , (x - 1) * 2 + 1
对于有向图其在读入的时候的边为 x , 链式前向星中的边的编号为 (x - 1) 。
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 1e5 + 10, M = 4e5 + 10;
int h[N], ne[M], e[M], idx;
int type, n, m, din[N], dout[N], cnt, res[M];
bool vis[M];
void add(int a, int b)
{
e[idx] = b, ne[idx] = h[a], h[a] = idx ++;
}
void dfs(int u)
{
for(int &i = h[u]; ~i; ){ // 通过引用 i = h[u], 来达到修改 h[u] 的目的。
if(vis[i]){
i = ne[i];
continue;
}
if(type == 1) vis[i ^ 1] = 1;
int t; // 获取边
if(type == 1){
t = i / 2 + 1;
if(i & 1) t = -t;
}else t = i + 1;
int j = e[i];
i = ne[i]; // 注意需要先获取当前边指向的点,然后更新当前边。
dfs(j);
res[++ cnt] = t; // 当遍历完所有边之后,回溯时将该边加入答案数组。
}
}
int main()
{
memset(h, -1, sizeof h);
cin >> type;
cin >> n >> m;
for(int i = 1; i <= m; i ++){
int a, b;
scanf("%d %d", &a, &b);
add(a, b);
if(type == 1) add(b, a);
din[b] ++, dout[a] ++;
}
if(type == 1){
for(int i = 1; i <= n; i ++)
if(din[i] + dout[i] & 1){
puts("NO");
return 0;
}
}else{
for(int i = 1; i <= n; i ++)
if(din[i] != dout[i]){
puts("NO");
return 0;
}
}
for(int i = 1; i <= n; i ++)
if(h[i] != -1){
dfs(i);
break;
}
if(cnt < m){
puts("NO");
return 0;
}
puts("YES");
for(int i = cnt; i >= 1; i --) printf("%d ", res[i]);
return 0;
}
注意起点的选择,是欧拉路径的话,需要从度为奇数的点作为起点出发。否则随意选择一个度为偶数的点出发。
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 510;
int g[N][N], d[N], res[1100], cnt, n;
void dfs(int u)
{
for(int i = 1; i <= 500; i ++){
if(g[u][i]){
g[u][i] --, g[i][u] --;
dfs(i);
}
}
res[ ++ cnt] = u;
}
int main()
{
cin >> n;
for(int i = 1; i <= n; i ++){
int a, b;
scanf("%d %d", &a, &b);
g[a][b] ++, g[b][a] ++;
d[a] ++, d[b] ++;
}
int sta = 1;
while(!d[sta]) sta ++ ;
for(int i = 1; i <= 500; i ++){
if(d[i] % 2){
sta = i;
break;
}
}
dfs(sta);
for(int i = cnt; i >= 1; i --) printf("%d\n", res[i]);
return 0;
}
建边:每个单词的首字母向最后一个字母连一条有向边。
想要保证单词之间的前后能够连起来,也就是要满足有向图的欧拉路径的条件,最后用并查集来判断连通性。
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 30;
int din[N], dout[N], n, T, f[N];
bool st[N]; // st数组用表示那些出现过
char str[1010];
int find(int x)
{
if(x != f[x]) f[x] = find(f[x]);
return f[x];
}
int main()
{
cin >> T;
while(T --){
cin >> n;
memset(din, 0, sizeof din);
memset(dout, 0, sizeof dout);
memset(st, 0, sizeof st);
for(int i = 0; i <= 26; i ++) f[i] = i;
for(int i = 1; i <= n; i ++){
scanf("%s", str);
int len = strlen(str);
int a = str[0] - 'a', b = str[len - 1] - 'a';
st[a] = st[b] = 1;
dout[a] ++, din[b] ++;
f[find(a)] = find(b);
}
bool flg = 1;
int start = 0, end = 0;
for(int i = 0; i < 26; i ++){ // 检查是否满足欧拉路径的条件。
if(din[i] != dout[i]){
if(din[i] == dout[i] + 1) end ++;
else if(dout[i] == din[i] + 1) start ++;
else{
flg = 0;
break;
}
}
}
if(flg && !(start == 0 && end == 0 || start == 1 && end == 1)) flg = 0;
int rep = -1; // 检查出现过的点是否都连通
for(int i = 0; i < 26; i ++){
if(st[i]){
if(rep == -1) rep = find(i);
else if(rep != find(i)){
flg = 0;
break;
}
}
}
if(flg) puts("Ordering is possible.");
else puts("The door cannot be opened.");
}
return 0;
}
拓扑排序
对一个有向无环图(Directed Acyclic Graph简称DAG)G进行拓扑排序,是将G中所有顶点排成一个线性序列,使得图中任意一对顶点u和v,若边[HTML_REMOVED]∈E(G),则u在线性序列中出现在v之前。
拓扑排序,我们只需要不断选择图中入度为 0 的节点 x,然后把 x 连向的点的入度减 1。
1、建立空的拓扑序列 A。
2、预处理出所有点的入度 deg[i],起初把所有入度为 0 的点入队。
3、取出队头节点 x,把 x 加入拓扑排序 A 的末尾。
4、对于从 x 出发的每条边 (x, y), 把 deg[y] 减 1。若被减为 0,则把 y 入队。
5、重复第 3~4 步直到队列为空,此时 A 即为所求。
拓扑排序可以判定有向图中是否存在环。我们可以对任意有向图执行上述过程,在完成后检查 A 序列的长度。若 A 序列的长度小于图中点的数量,则说明某些节点未被遍历,进而说明图中存在环。
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<queue>
using namespace std;
const int N = 110, M = N * N;
int h[N], ne[M], e[M], idx;
int d[N], a[N], n, cnt;
void add(int a, int b)
{
e[idx] = b, ne[idx] = h[a], h[a] = idx ++;
}
void topsort()
{
queue < int > q;
for(int i = 1; i <= n; i ++){
if(!d[i])
q.push(i);
}
while(q.size()){
int t = q.front();q.pop();
a[ ++ cnt] = t;
for(int i = h[t]; ~i; i = ne[i]){
int v = e[i];
if(-- d[v] == 0) q.push(v);
}
}
}
int main()
{
memset(h, -1, sizeof h);
cin >> n;
for(int i = 1; i <= n; i ++){
int x;
while(cin >> x, x){
add(i, x);
d[x] ++;
}
}
topsort();
for(int i = 1; i <= cnt; i ++) printf("%d ", a[i]);
return 0;
}
因为边权都是大于 0 的正数,所以可以用拓扑排序来判断图中有没有环,如果图中有环则说明题目无解。
在求完拓扑排序之后,我们就已经确定了员工之间的大小关系,然后我们就可以拓扑排序之后的序列来求最长路即可。
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<queue>
using namespace std;
const int N = 1e4 + 10, M = 2e4 + 10;
int h[N], ne[M], e[M], idx;
int d[N], res[N], cnt, n, m, dis[N];
void add(int a, int b)
{
e[idx] = b, ne[idx] = h[a], h[a] = idx ++;
}
bool topsort()
{
queue < int > q;
for(int i = 1; i <= n; i ++)
if(!d[i]){
q.push(i);
}
while(q.size()){
int t = q.front();q.pop();
res[cnt ++] = t;
for(int i = h[t]; ~i; i = ne[i]){
int v = e[i];
if(-- d[v] == 0) q.push(v);
}
}
return cnt == n;
}
int main()
{
memset(h, -1, sizeof h);
cin >> n >> m;
for(int i = 1; i <= m; i ++){
int a, b;
scanf("%d %d", &a, &b);
add(b, a);
d[a] ++;
}
if(!topsort()) puts("Poor Xed");
else{
int sum = 0;
for(int i = 1; i <= n; i ++) dis[i] = 100;
for(int i = 0; i < cnt; i ++){
int v = res[i];
for(int j = h[v]; ~j; j = ne[j])
dis[e[j]] = max(dis[e[j]], dis[v] + 1);
}
for(int i = 1; i <= n; i ++) sum += dis[i];
cout << sum << endl;
}
return 0;
}
f(x) 表示从点 x 出发能够到达的点构成的集合。
$$
f(x) = \{x\} \bigcup \left\( \bigcup_{存在有向边(x, y)} f(y)\right\)
$$
从 x 出发能够到达的点,是从 “x的各个后继节点 y” 出发能够到达的点的并集,再加上点 x 自身。所以,在计算出一个点的所有后继节点的 f 值之后,就可以计算出该点的 f 值。所以可以先用拓扑排序算法求出一个拓扑序,然后按照拓扑序的倒序进行计算——因为在拓扑序中,对任意的一条边 (x, y) ,x 都排在 y 之前。
使用一个 N 位二进制数存储每个 f(x) ,其中第 i 位是 1 表示 x 能到 i ,0 表示不能到 i 。这样求并集运算就相当于对若干个 N 位二进制数做 “按位或” 运算。最后每个 f 值中 1 的个数就表示 x 出发能够到达的节点数量。
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<queue>
#include<bitset>
using namespace std;
const int N = 3e4 + 10;
int h[N], ne[N], e[N], idx;
bitset < N > f[N];
int d[N], n, m, res[N], cnt;
void add(int a, int b)
{
e[idx] = b, ne[idx] = h[a], h[a] = idx ++;
}
void topsort()
{
queue < int > q;
for(int i = 1; i <= n; i ++)
if(!d[i]) q.push(i);
while(q.size()){
int t = q.front();q.pop();
res[cnt ++] = t;
for(int i = h[t]; ~i; i = ne[i]){
int v = e[i];
if(-- d[v] == 0) q.push(v);
}
}
}
int main()
{
memset(h, -1, sizeof h);
cin >> n >> m;
for(int i = 1; i <= m; i ++){
int a, b;
scanf("%d %d", &a, &b);
add(a, b);
d[b] ++;
}
topsort();
for(int i = cnt - 1; i >= 0; i --){
int j = res[i];
f[j][j] = 1;
for(int k = h[j]; ~k; k = ne[k]){
int v = e[k];
f[j] |= f[v];
}
}
for(int i = 1; i <= n; i ++) printf("%d\n", f[i].count());
return 0;
}
题目要求的是 始发站、终点站之间所有级别大于等于火车站x的都必须停靠,也就是说停靠过的车站一定要大于未停靠的车站。
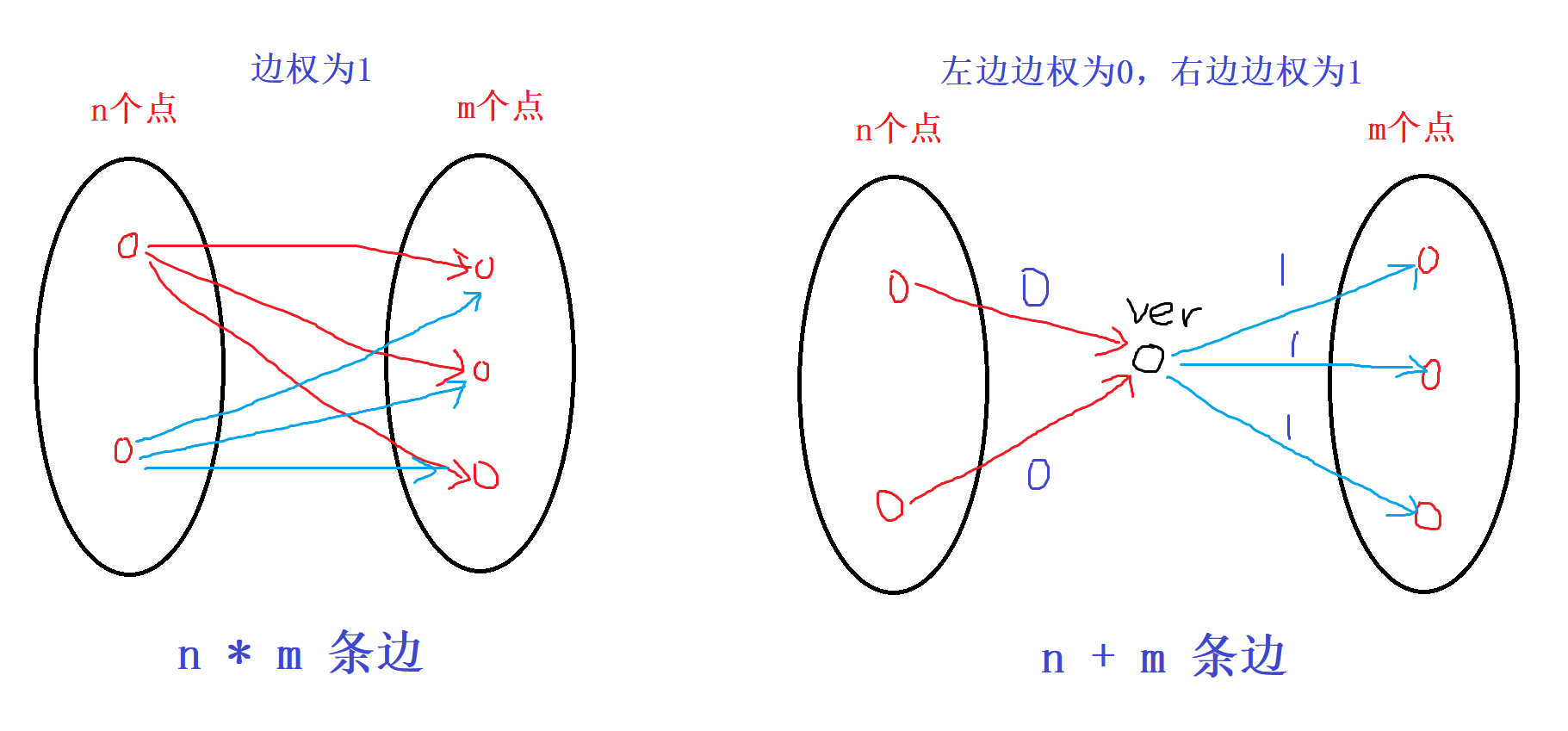
建边 :所有未停靠过的车站向停靠过的车站建一条边,但是这样建边的空间和时间复杂度都太高了。所以可以通过中间建立虚拟点来解决。
下图转自小呆呆题解。
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<queue>
using namespace std;
const int N = 2e3 + 10, M = N * N;
int h[N], ne[M], e[M], w[M], idx;
int d[N], dis[N], res[N], cnt, n, m;
bool st[N];
void add(int a, int b, int c)
{
e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++;
d[b] ++ ;
}
void topsort()
{
queue < int > q;
for(int i = 1; i <= n + m; i ++)
if(!d[i]) q.push(i);
while(q.size()){
int t = q.front();q.pop();
res[cnt ++] = t;
for(int i = h[t]; ~i; i = ne[i]){
int v = e[i];
if( -- d[v] == 0) q.push(v);
}
}
}
int main()
{
memset(h, -1, sizeof h);
cin >> n >> m;
for(int i = 1; i <= m; i ++){
memset(st, 0, sizeof st);
int num;
scanf("%d", &num);
int a = n, b = 1;
while(num --){
int x;
scanf("%d", &x);
a = min(a, x);
b = max(b, x);
st[x] = 1;
}
int ver = n + i;
for(int j = a; j <= b; j ++){
if(!st[j]) add(j, ver, 0);
else add(ver, j, 1);
}
}
topsort();
for(int i = 1; i <= n; i ++) dis[i] = 1;
for(int i = 0; i < n + m; i ++){
int j = res[i];
for(int k = h[j]; ~k; k = ne[k])
dis[e[k]] = max(dis[e[k]], dis[j] + w[k]);
}
int res = 0;
for(int i = 1; i <= n; i ++) res = max(res, dis[i]);
cout << res << endl;
return 0;
}


欧拉回路里面你少一个vis[i]=true