次小生成树
严格次小生成树: 给定一个无向带权图, 把图的所有生成树按权值大小从小到大排序, 权值大小排名第二的生成树
非严格次小生成树: 给定一个无向带权图, 把图的所有生成树按权值大小从小到大排序, 第二个生成树
方法
由于Prim, Kruscal算法保证, 中间过程的生成树也是局部最小生成树, 那么也就是说次小生成树与最小生成树只差一条边,但相差的可能时是最大权值边, 也可能是次大权值边, 但绝不可能是其他边了, 因为这样最小生成树就变化了, 其他边都相等, 可以看下图自行分析。
波浪线为最小生成树, 双横线为次小生成树
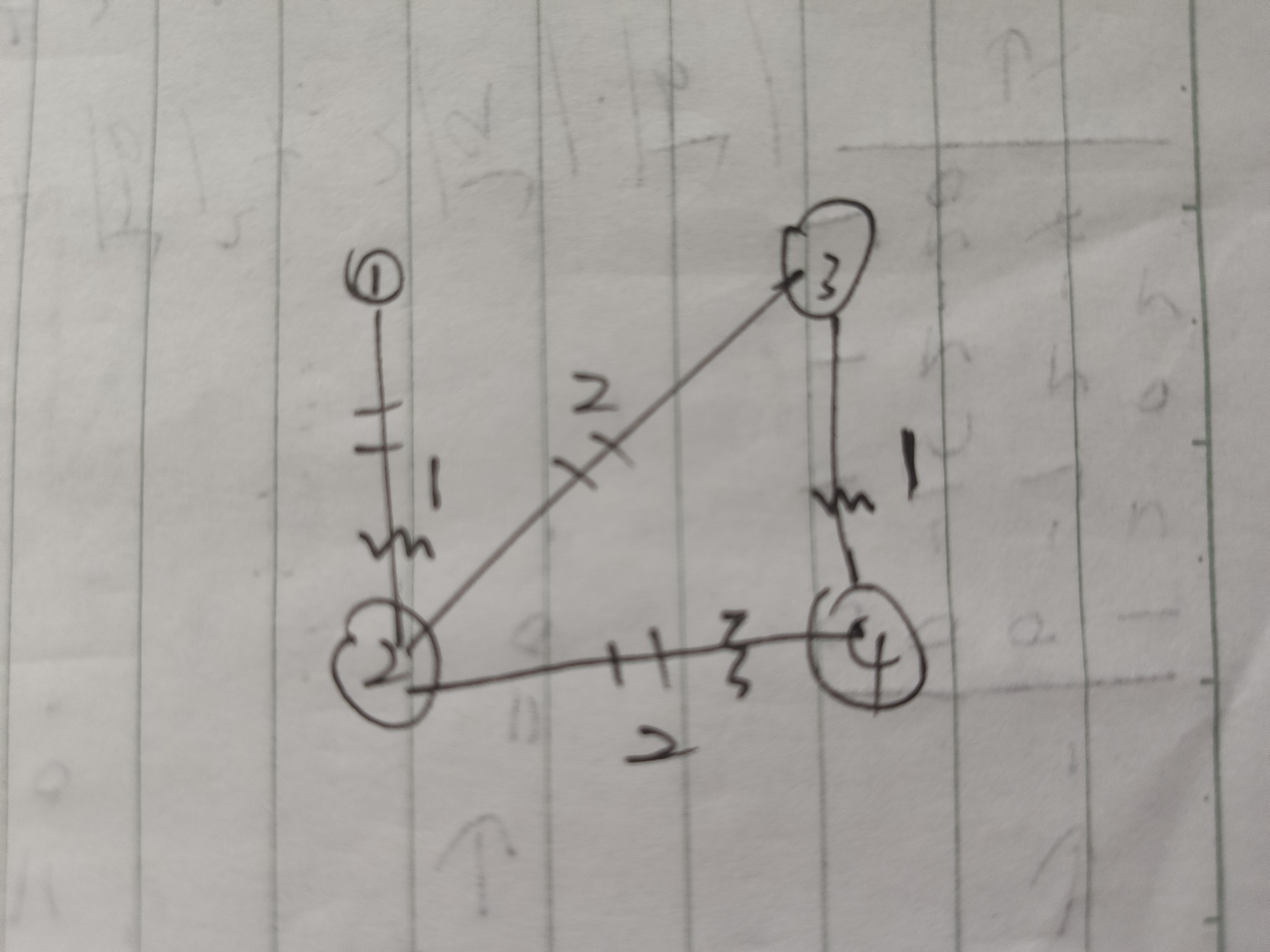
写在前面, 非树边为m, n为结点数。
- way1 (-a +b 先删再加): 先求出最小生成树, 依次枚举最小生成树中的一条边, 将其替换为非树边中的某一条可行边,对权值和取一个min即可。 $O(mlogn + nm)$
不能求严格次小生成树原因: 因为假如你替换的边等于删除边, 同时, 严格次小生成树, 也是需要替换该边, 但是严格次小的替换边的权值大于非严格次小的替换边权值, 所以就不会被换上, 导致严格次小无法求出,即 权值和 集合并不能包含所有差一条边的生成树。
- way2 (+a -b 先加再删): 先求最小生成树, 再枚举非树边, 加入生成树, 同时删除最小生成树中新加边所在环(树加上一条边就一定有环了)中的最大权值边或次大权值边(预处理出来每两个点之间的最大权值边和次大权值边, 每个点到其他点(n - 1, n - 2, … , 1)的路径只有一条, 有n个点, 时间复杂度为n^2), 使得原图依然为一个树。在这些生成树 权值和 集合(最小生成树的邻集, 其中既包含了非严格次小生成树, 也包含了严格次小生成树,因为加边时严格非严格的替换边都会加进去,删同一条边形成两颗次小生成树)中选取次小生成树的类型输出即可。$O(m + n^2 + mlogn)$
在求树中两点之间的极值边, 可用动态树, 树链剖分, LCA(倍增法) O(mlogn)

