今天系统写一个数塔算法的笔记

搜索法

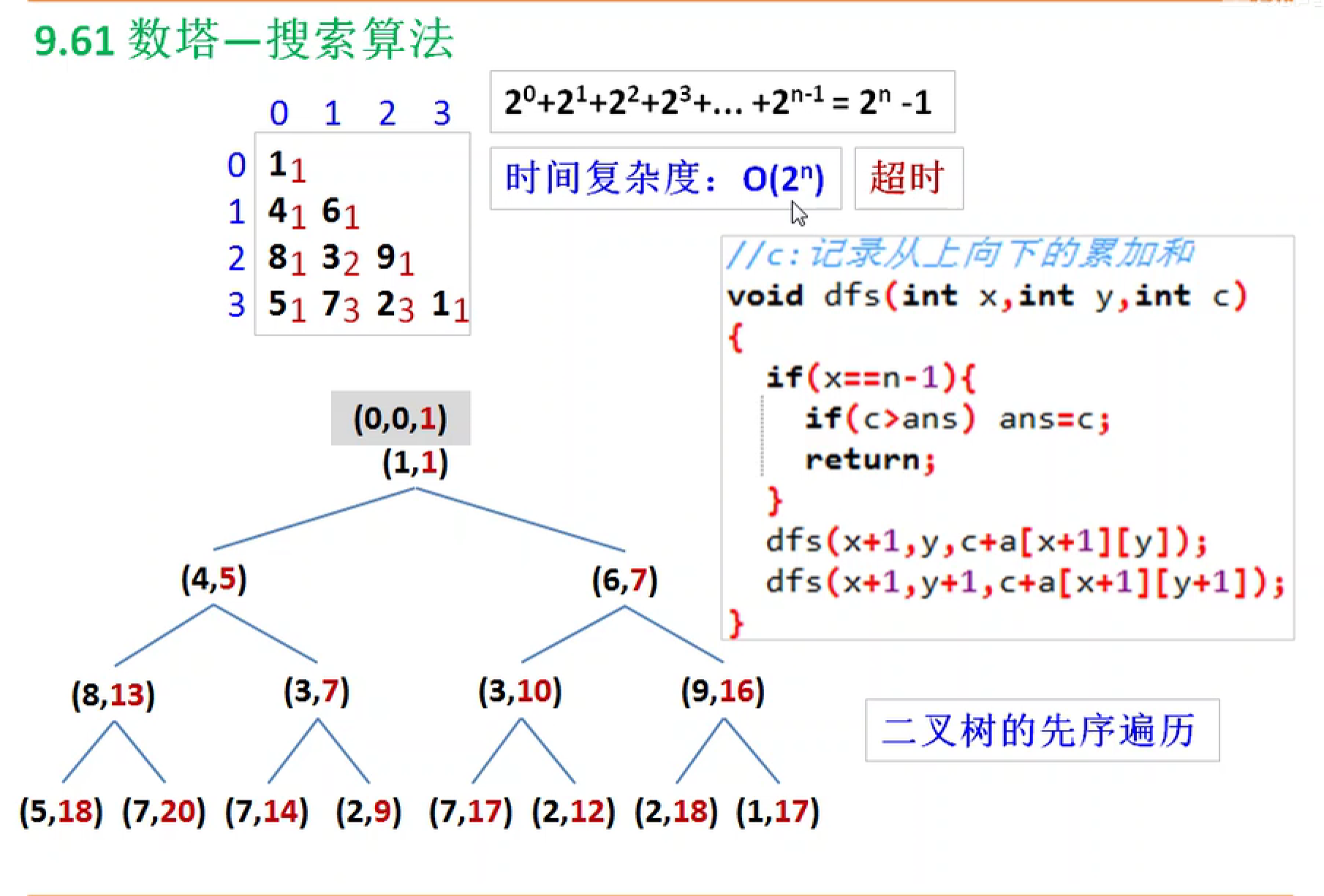
这里我自己写了一下题解(时间复杂度好高2^n)

#include <iostream>
#include <cstring>
#include <algorithm>
#include <map>
using namespace std;
int a[9][9]={{1},{4,6},{8,3,9},{5,7,2,1}};//先将这个数组进行初始化
int n=4;
int ans=0; 
void dfs(int x,int y,int c)
{
    if(x==n-1)//如果这里的行数为n-1的我们就要退出了，当然我们在这里要进行判断最大值
    {
        if(c>ans)
        {
            ans=c; 
        }
        return;
    } 
    dfs(x+1,y,c+a[x+1][y]);
    dfs(x+1,y+1,c+a[x+1][y+1]);
}
int main()
{
    //接下来进行这里的搜索算法
    dfs(0,0,a[0][0]); 
    cout<<"最大的搜索路径为:"<<ans<<endl;
    return 0;
} 

剪枝算法

我们发现一个规律就是自上向下的这些结点是不能重复使用的，而自下向上的算法是可以重复使用的

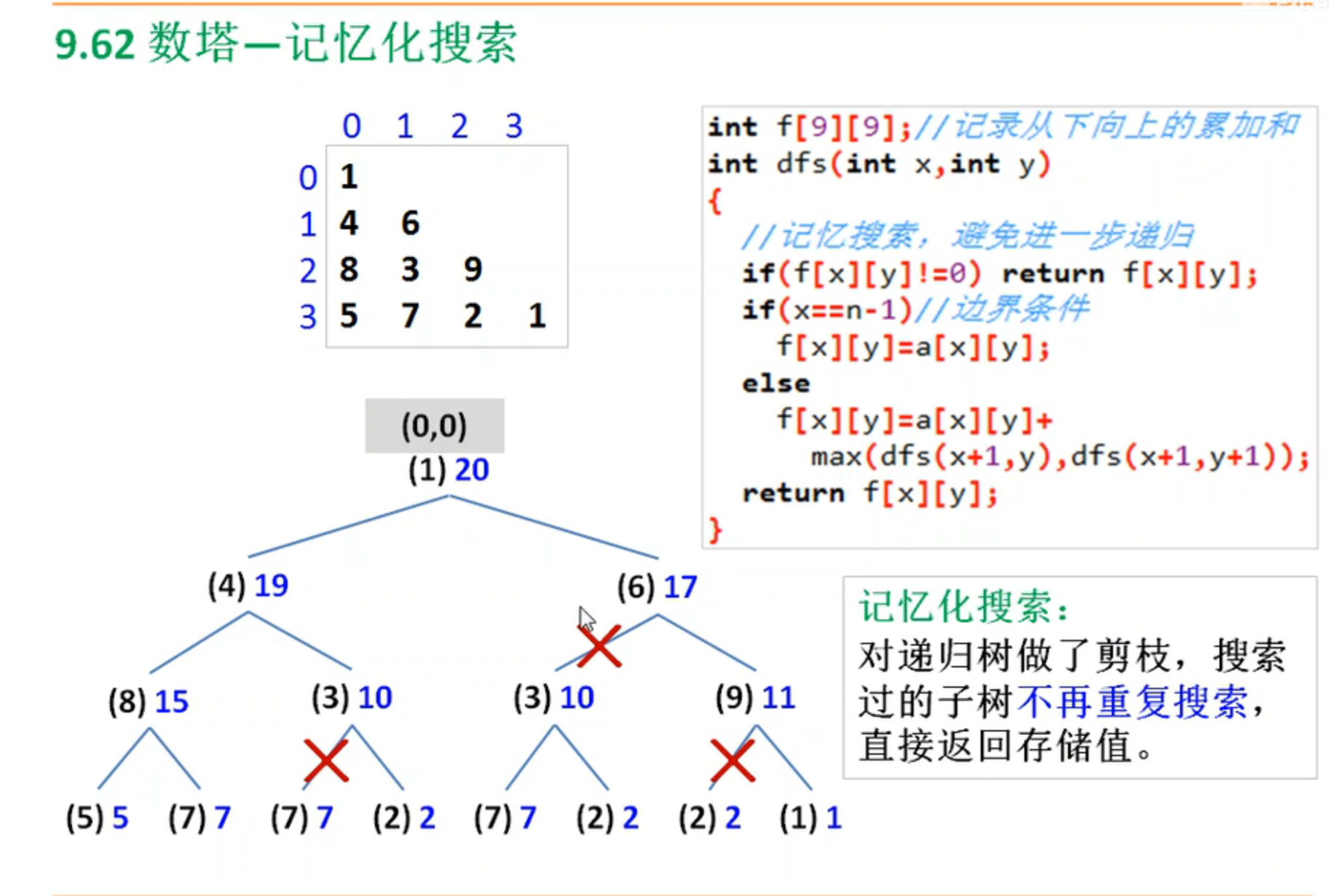
#include <iostream>
#include <cstring>
#include <algorithm>
#include <map>
using namespace std;
int a[9][9]={{1},{4,6},{8,3,9},{5,7,2,1}};//先将这个数组进行初始化
int n=4;
int f[9][9];//用于记录每一个位置的最大数 
int dfs(int x,int y)
{
    if(f[x][y]!=0)//如果这个点已经被访问过的话，我们就直接将这个记忆化的值返回
    {
        return f[x][y];
    }//这里就是剪枝的精髓所在
    if(x==n-1)
    {
        f[x][y]=a[x][y];
    }      
    else
    {
        f[x][y]=a[x][y]+max(dfs(x+1,y),dfs(x+1,y+1));
    }
    return f[x][y];//这里也是从上向下进行的深搜 
}
int main()
{
    //接下来进行这里的搜索算法
    dfs(0,0); 
    cout<<"最大的搜索路径为:"<<f[0][0]<<endl;
    return 0;
} 

第三个就是这里的逆推法，给出这里的一个题目-数字三角形

https://www.acwing.com/problem/content/description/900/

给出这里的题解

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 510;
int a[N][N];
int f[N][N];//来进行计算
int n;
int main()
{
    cin >> n;
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=i;j++)
        {
            cin>>a[i][j];
        }
    }
    //将这个边值进行初始化
    for(int i=1;i<=n;i++)
    {
        f[n][i]=a[n][i];
    }
    //然后进行我们的逆推的方法
    for(int i=n-1;i>=1;i--)
    {
        for(int j=1;j<=i;j++)
        {
            f[i][j]=a[i][j]+max(f[i+1][j],f[i+1][j+1]);
        }
    }
    cout<<f[1][1]<<endl;
    return 0;
}

https://www.acwing.com/problem/content/description/900/ 运用上述的顺推法

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 510;
const int INF =0x3f3f3f3f;
int a[N][N];
int f[N][N];//来进行计算
int n;
int main()
{
    cin >> n;
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=i;j++)
        {
            cin>>a[i][j];
        }
    }
    //因为这里有负数，因此我们要将两边的值取为负无穷大
    for(int i=1;i<=n;i++)
    {
        for(int j=0;j<=i+1;j++)
        {
            f[i][j]=-INF;
        }
    }
    //因为有负数嘛
    f[1][1]=a[1][1];
    for(int i=2;i<=n;i++)
    {
        for(int j=1;j<=i;j++)
        {
          f[i][j]=max(f[i-1][j-1],f[i-1][j])+a[i][j];
        }
    }
    //然后再最后一层寻找最大的值
    int  ans=-INF;
    for(int i=1;i<=n;i++)
    {
        ans=max(ans,f[n][i]);
    }
    cout << ans<<endl;
    return 0;
}