找规律

已知两点 $(x_1, y_1)$、$(x_2, y_2)$
这两点间的 曼哈顿距离 为：$|x_1-x_2|+|y_1-y_2|$。

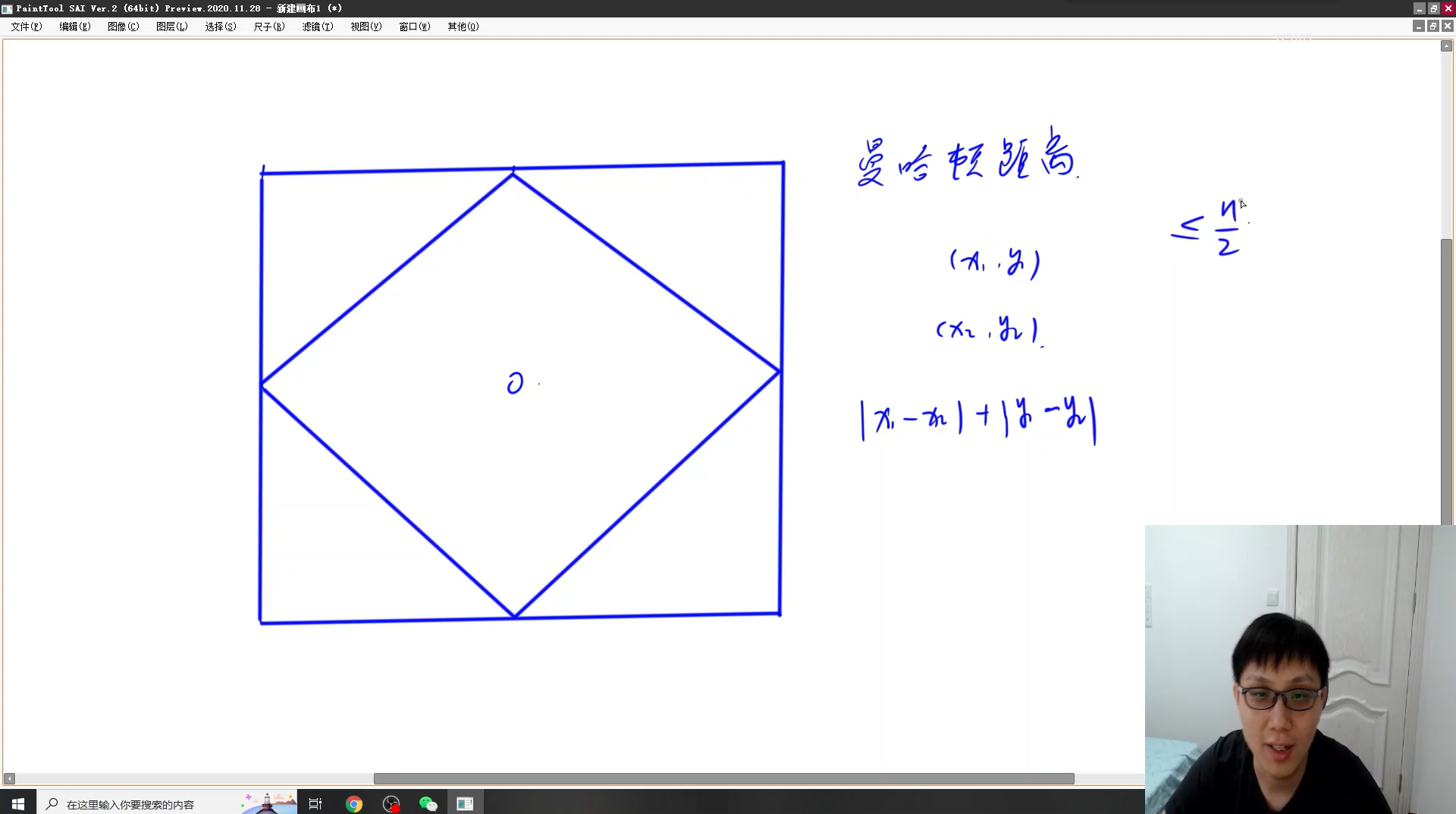
通过观察，我们可以发现需要填充*的位置，到中心点的曼哈顿距离都小于n/2（也就是中心点到边的距离）；而其他位置则填充空格。

不管下标是从0开始还是从1开始，中心到边的距离都是不变的：等于中心的横坐标-同一行最左侧点(或最右侧)的横坐标。

下标从0开始

import java.util.Scanner;

public class Main{
    public static void main(String[] args){
        Scanner sc = new Scanner(System.in);
        int n=sc.nextInt();
        int cx=n/2, cy=n/2;
        for(int i=0; i<n; i++) {
            for (int j=0; j<n; j++) {
                int dist = Math.abs(i-cx)+Math.abs(j-cy);
                if (dist <= n/2)
                    System.out.printf("*");
                else
                    System.out.printf(" ");
            }
            System.out.printf("\n");
        }
    }
}

下标从1开始

import java.util.Scanner;

public class Main{
    public static void main(String[] args){
        Scanner sc = new Scanner(System.in);
        int n=sc.nextInt();
        int cx=n/2+1, cy=n/2+1; //中心点的坐标
        for(int i=1; i<=n; i++) {
            for (int j=1; j<=n; j++) {
                int dist = Math.abs(i-cx)+Math.abs(j-cy);
                if (dist <= n/2)
                    System.out.printf("*");
                else
                    System.out.printf(" ");
            }
            System.out.printf("\n");
        }
    }
}