写在前面,
祖先包括其本身

解决问题

求一个有根树中, 任意两个点的最近公共祖先
(树不一定是二叉树, 但是固定节点的二叉树的深度(是最小的, logn)一定比多叉树的深度大, 所以logn就可以作为数组fa[i][k], 其中k的最大维度, 最大值了)

解决算法

• 向上标记法 $O(n) - 两条链$

  用一个bool数组标记, 先对一个点的所有祖先全部标记, 再遍历另一个点的所有祖先, 当第一个祖先被标记时, 它就是最近公共祖先.

• 倍增 (查询一个, 输出一个, 在线)

  1）预处理一个fa数组, 一个depth数组.
  2）这里我们需要注意, 我们看一个数a的二进制是多少的时候, 可以将2^0, 2^1, … , 2^n列出来, 用a从大到小比大小, 第一个比他大的2^i, 就表示a这个数的二进制表示形式的第i位为1, 我们将这个数减去, 继续向下比, 直至a被减为0, 二进制表示也就随之得出了.
  3) 预处理fa数组利用递推的思想, fa[i][k]等价于fa[fa[i][k - 1]][k - 1]
  
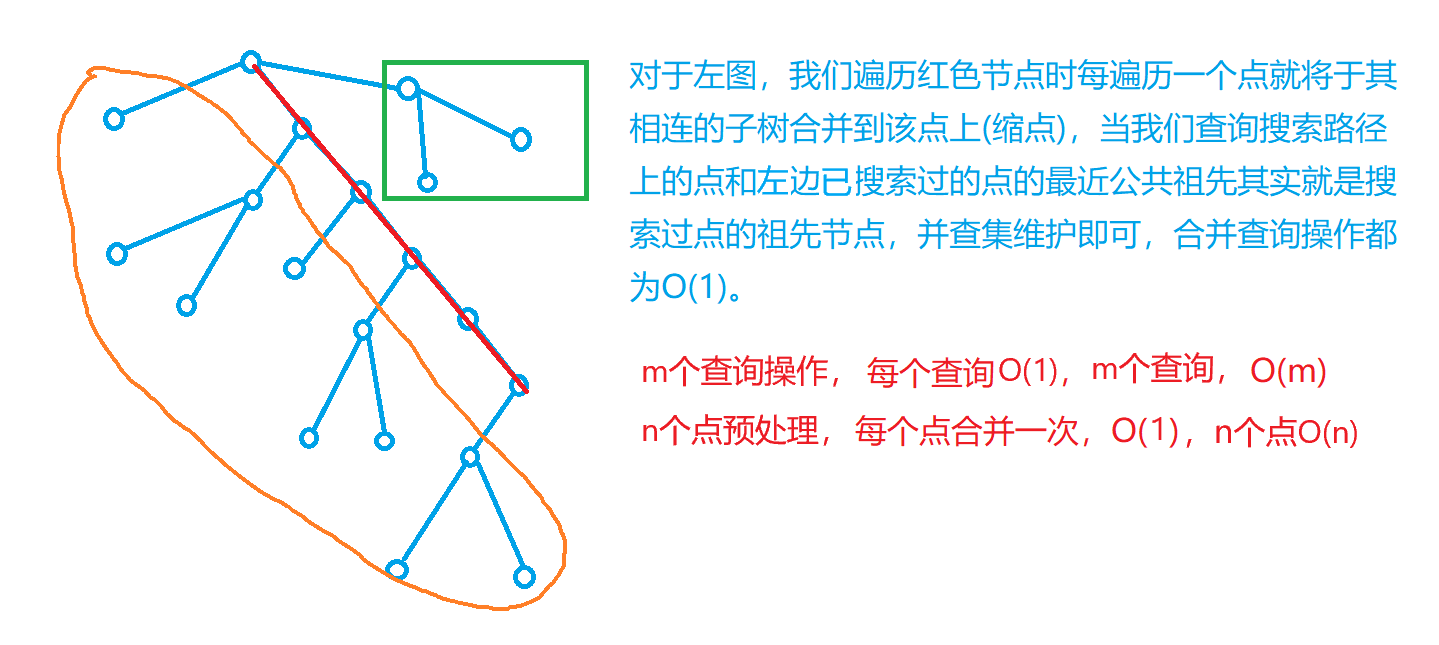
  例题

• tarjan求LCA (读入所有查询, 统一输出, 离线)

  预处理时间复杂度: $O(n)$
  询问时间复杂度: $O(1)$
  
  算法思想
  
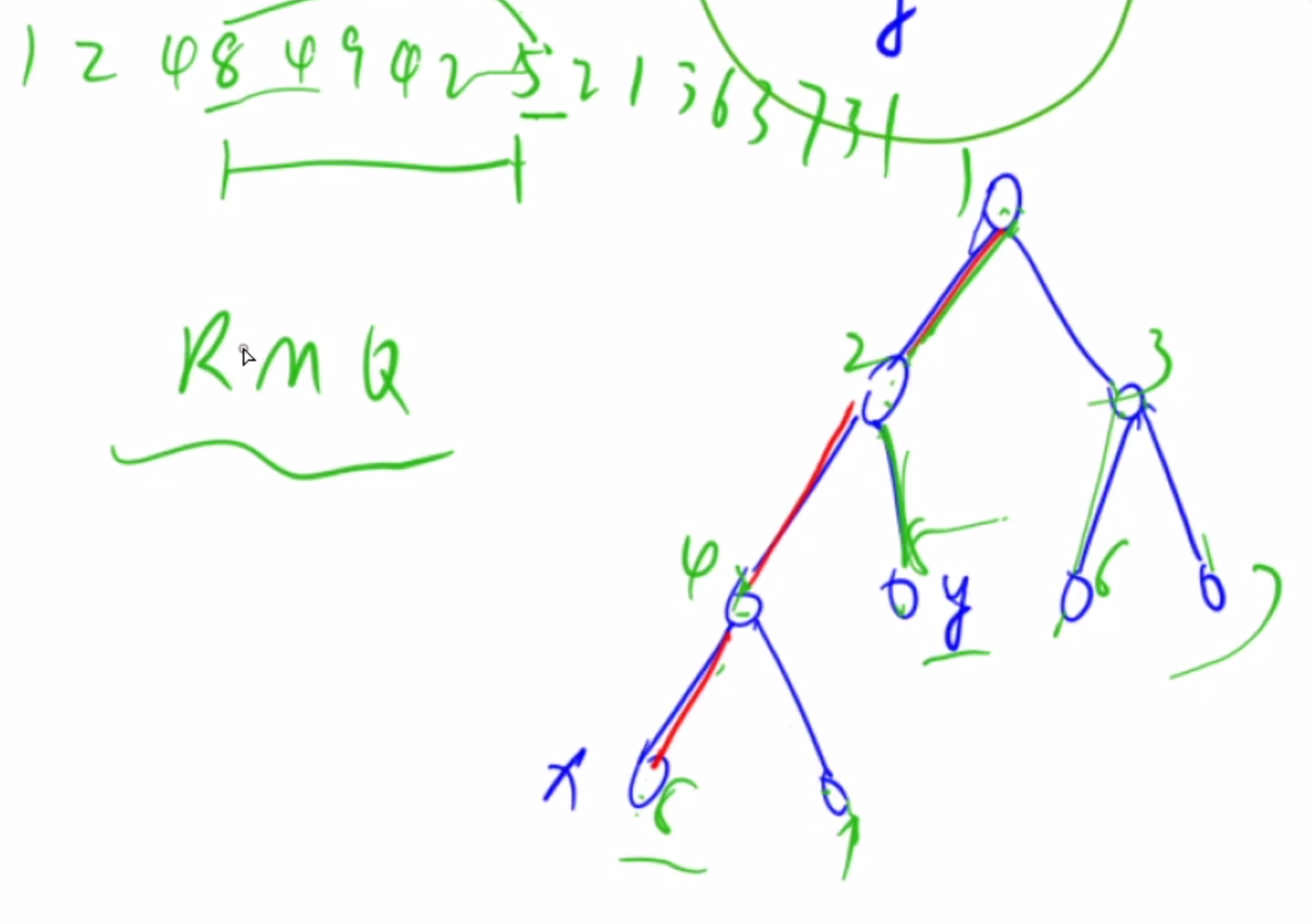
  例题

• RMQ

  我们先对树的每个节点打上编号, 然后我们对树跑一遍dfs, 用一个数组记录先序遍历节点编号序列$O(n)$, 两节点的最近公共祖先就是在序列中的对应两点的区间中的最小值(深度最小的点) -> 查询静态区间最值: 线段树预处理查询都是$O(logn)$, RMQ预处理$O(nlogn)$, 查询$O(1)$